从简单到夏杂——名副其实的基本不等式

沙国祥

数学中，被冠以“基本”二字的定理、公式、法则屈指可数，不然就对不起这“基本”的意思了.基本不等式b≥0），就是其中之一.我们来看看其“基本”之处究竟在哪儿.

首先，除了基本不等式，还有一些比较重要的不等式，可以由此推演而来.如：

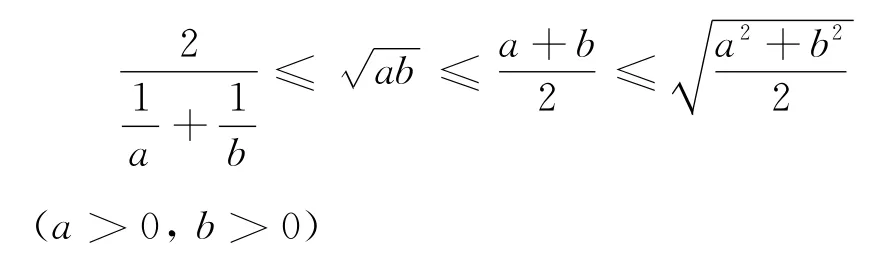
都能用基本不等式加以证明，可见，基本不等式不愧为基本中的基本！

例如，sinθ+cosθ（θ∈R）的最大值是_____.由于sinθ与cosθ之间有基本的平方和关系sin2θ+cos2θ=1，所以，由可得因此.当时，所以sinθ+cosθ可取最大

你看，对sinθ+cosθ（θ∈R）我们一时难以下手，但你必定知道相关的等式sin2θ+cos2θ=1，要充分利用！于是，自然想到将sinθ+cosθ平方，得 （sinθ+cosθ）2=1+2sinθcosθ，这时，出现了sinθ和cosθ的乘积sinθcosθ，由基本不等式得2sinθcosθ≤sin2θ+cos2θ=1，所以（sinθ+cosθ）2≤2，

其次，基本不等式可直接或经过变形后用于证明不等式或求函数的最值等问题.

我们来看这样的例子：

对于第（1）问，该函数的定义域为（1，+∞），直接利用基本不等式，可得y≥2，且x=2时，y的最小值为2.

对于第（2）问，该函数的定义域为（1，+∞）.若要利用基本不等式，须将拆成两部分，使其乘积为定值.向分母靠拢，得

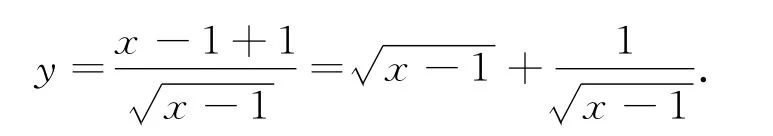
这不就转化成问题（1）了吗？

又如，设x为锐角，求

这个不等式的左端很有意思，三种基本三角函数sinx，cosx，tanx齐上阵，如果直接用基本不等式，是得不到结论的（你不妨一试）.我们利用三角公式化简，设法减少异名三角函数的个数：

再运用基本不等式立得结论.

再次，基本不等式的运用隐身于各种复杂的方程、函数问题的求解中.

例如，已知a＞b≥c≥0，且则a+b+c=___________.

这道题很特别，给出了一个十分复杂的方程，其中有三个未知数，乍看非常吓人！你可能会有疑问：能够一石三鸟，求出a，b，c的值吗？再说，条件给出的是一个方程，哪里有基本不等式的影子呢？

我们退一步来看一个简单的类似问题（学数学时，我们常常从简单的问题悟出道理，再将其用于解决复杂的问题）：已知a2+（b-1）2+（c-2）2=0这一个方程，就能够一举确定三个未知数a，b，c的值.这个方程好强悍！它有什么特别之处呢？注意：当a，b，c都是实数时，a2≥0，（b-1）2≥0，（c-2）2≥0，所以a2+（b-1）2+（c-2）2≥0，等号当且仅当其中的三个完全平方式都为0时才成立，即当a2+（b-1）2+（c-2）2=0时，必有a=b-1=c-2=0，a=0，b=1，c=2.

等号当且仅当a（a-b）=1，ab=1，a-2c=0时成立，又a＞b≥c≥0，解得a=则

回顾一下，我们利用基本不等式，由简单到复杂（或有时先化复杂为简单，再从简单到复杂），解决了一些比较复杂的不等式、函数问题.好比一条小溪，不断弯曲流淌，沿途汇入无数小溪、小河，直至变成大河大江，虽浩浩荡荡、波浪翻滚，其源头却是清晰、简单的.