解析几何中含定比分点问题的解法分析
2019-12-24南京市第九中学张荣彬
南京市第九中学 张荣彬
已知P,A,B是直线上的三个点,若则称P为有向线段AB的定比分点.
在解析几何中,同学们经常会遇到含定比分点的问题.此类问题的表面特征常常是带有向量的等式,因此解决的方法就是“去向量化”,将问题转化为几何或代数(坐标)的形式来解决.
一、解法展示
例1已知曲线E:ax2+by2=1(a>0,b>0),经过点M(m,0)的直线l与曲线E交于点A,B,且
分析先看第(1)问:
思路1:因A,B两点均在圆上,故A,B两点的坐标均满足圆的方程,于是有消去y1解得x1=回代得所以
思路2:由题意可知,直线l与x轴不垂直,所以可设直线l的方程为y=k(x-1),联立方程组消去y得 (1+k2)x2-2k2x+k2-4=0,由韦达定理得将x2=3-2x1代入得x1+x2=3-x1=消去x1可解得
思路3:因AB是圆E的一条弦,如图1,可使用垂径定理,取AB的中点D,则OD⊥AB.设OD=d,MA=t,则MB=2t,DM=因OM=1,OB=2.所以
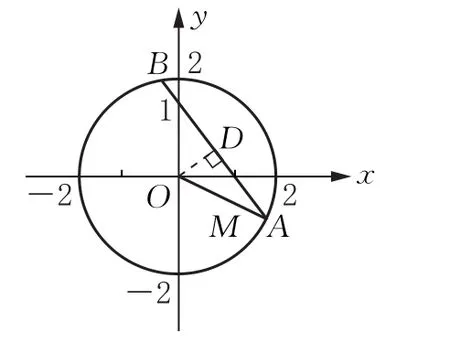
图1
设l:y=k(x-1),即kx-y-k=0,则解得
再看第(2)问:
仿(1)的思路2将直线y=k(x-1)与椭圆的方程联立消去y得(3+4k2)x2-8k2x+4k2-12=0,同样可解;
能否用几何的方法将本题用(1)中的思路3完成?椭圆中可没有垂径定理啊,失望之余突然又看到希望:原来点M(1,0)恰好是椭圆的右焦点,如图2.设椭圆的右准线为s,过A,B分别向s作垂线,垂足分别是A1,B1,设AM=t,则BM=2t,因椭圆的离心率由椭圆的第二定义得AA1=2t,BB1=4t,再过点A作AD⊥BB1于D,则BD=2t,在Rt△ABD中,tan∠ABD=于是
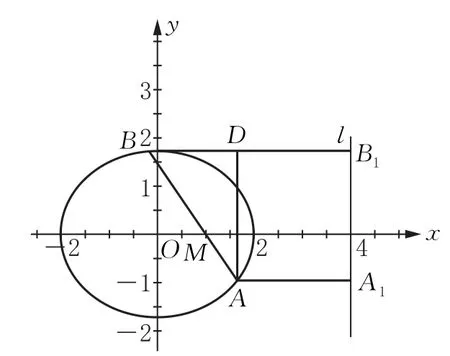
图2
二、方法归纳
求解含定比分点的问题,主要就是使用上述例1中的三种方法:
1.通过定比分点发现几何关系,利用平面几何或圆锥曲线的有关知识完成;关系2,.
利将用定曲比线分上点点转的化坐为标相满关足点曲间线的方坐程标,列出3方.程将组相求关解点;所在直线与曲线的方程联立,借其助转韦化达思定路理消可元用完图成3.所示的流程图表示.
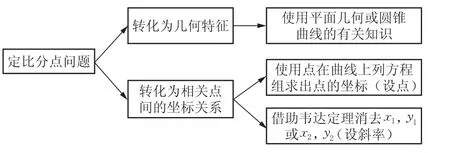
图3
由于题目条件呈现的方式不同,在遵循以上解题思想的基础上,对于方法的选择及某些细节的处理上会有所变化.
三、变式应用
例2如图4,在平面直角坐标系xOy中,已知椭圆的离心率为,C为椭圆上位于第一象限内的一点.设A为椭圆的左顶点,B为椭圆上一点,且求直线AB的斜率.
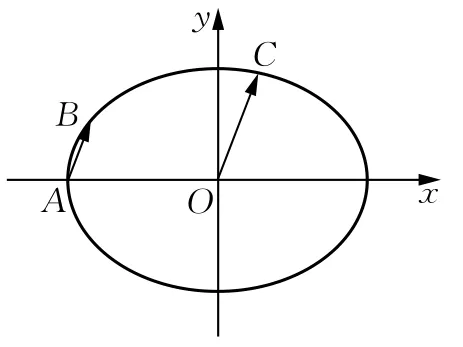
图4
分析因为椭圆的离心率为,所以,即
因此椭圆的方程可化为5x2+9y2=5a2,则A(-a,0).设B(x1,y1),C(x2,y2).则由得(x1+a,y1)=,所以.因为点B和点C都在椭圆5x2+9y2=5a2上,所以算可得直线AB的斜率
本题的求解也可从向量关系中获取AB∥OC,OC=2AB的信息,通过设斜率,求弦长来完成,显然其计算量较大.
四、反馈拓展
以向量为载体的定比分点问题面广量大,题型也灵活多变,有时定点未知,有时比值未知,有时会出现多个定比的现象,其解决方法大同小异,为了让同学们能更好地把握,需要再次强化:
方法1是几何法.从向量关系中可读出特殊的点,特殊的比值,此法简捷,为第一选择;
方法2是设点法.根据向量等式写出两点坐标关系(横和纵)⇒分别代入曲线方程⇒解方程组求出点的坐标,如例1和例2.在使用这个方法时同学们往往会畏惧求解二元二次方程组,事实上这个方程组往往较容易转化为一元一次方程求解,要掌握其中的玄机;
方法3是设k法.设出直线方程⇒将直线与曲线方程联立⇒使用韦达定理⇒利用由向量翻译出来的坐标关系(横或纵)⇒消元解出k.
有时,题目中出现的定比关系是“假”的,仅仅是表面的外衣,可以直接无视;有时题中并没有出现上面所说的定比分点问题,但根据解题需要也可以把它转换到这个解题套路中来,从而不断扩大自己成熟的解题领域.计
