基于数学核心素养
2019-12-23陈忠仕
陈忠仕
摘 要:图形变换是将几何图形按照某种规律或法则运动变化的数学抽象。新课标突出了初中数学图形变换的内容和要求,要求熟练掌握图形变换,从变换的角度寻找解题思路。图形变换教学要关注学生的核心素养,积极探究符合学生认知特点的教学策略和方法。
关键词:初中数学;图形变换;策略与反思;核心素养
图形变换是对图形一种合理性的演绎推理,学生在变换中获取信息,在运动中思考问题。图形变换教学要抓住静态图形与动态图形的转化,变换前后点、线段、角建立起的数量关系和位置关系变化,抓住概念的本质,理解运动变换的理念与思想[1]。下面就核心素养下“图形变换”的教学策略与反思进行简述,目的是积累经验,使图形变换在教学中更为具体化和形象化。
一、“图形变换”的教学定位与价值
小学教材注重图文结合,大多以活动的形式理解图形变换。初中数学图形变换重视观察、操作、想象、推理、表达之间的结合,加强概念教学,把握知识联系,在识图、绘图中探究变换性质,形成解题策略,发展几何直觉和空间观念。
做好中小学“图形变换”的教学衔接。在教学内容上做好从小学教材直观、形象到中学教材丰富、抽象的自然过渡,有的放式、承前启后。教学方法上要引导学生联系生活实际,采取循序渐进的教学原则,做好从小学试验几何到中学论证几何的过渡,强化逻辑推理上的衔接。
二、“图形变换”的教学策略探究
图形变换是图形与几何的重要组成部分,无论从语言描述、图形刻画都要加强对图形运动变换的理解,深化图形变换的教学策略探究。
1.重视教材理解,透析概念本质
图形变换的教学要采用循序渐进的原则,由较为简单的“平移和轴对称”过渡到“旋转”,教学中要将文字、符号、图形三者结合起来理解,并能自由转化,避免因认知结构导致对三种数学语言的理解割裂。
(1)依托教材,探究平移性质
平移变换要抓住平移方向和平移距离这两个关键因素,明确移动的点、线、面都具有相同的移动向量。借助方格或坐标系理解平移的性质学生比较容易接受。如一个图形在平面直角坐标系中沿x轴方向平移a(a>0)个单位,观察对应点的坐标变化?如果图形沿y轴方向平移a(a>0)个单位呢?借助坐标系探究图形平移与坐标变化,提升学生思维品质。
(2)联系生活,体验对称之美
联系生活实际,如展示自然界中具有对称属性的实物:鸟类翅膀、蝴蝶标本、雪花晶体、飞机模型等;举例生活中的对称图形:如口、日、目、B、E、S、3、0、8等;判断正多边形的对称性,并指出对称轴;开展剪窗花、折纸等活动;还可以由一些基本图案设计轴对称图形或中心对称图形体验对称美,理解对称性质。
(3)动手操作,直观体验旋转
旋转变换教学不重概念,应通过演示和操作,体会旋转中心和旋转角度的变与不变,感知旋转变换性质。
案例:剪下两张全等三角形纸片如下图摆放,对其中一个三角形进行旋转变换使之与另一个三角形重合,思考对应边对应角的变化。
设计意图:经过多次操作、反复体验、感知旋转变换的概念和性质,追击运动本质。教学中引导学生想象与操作结合,从“动手操作”到“想象作图”,达到“手中无剑”到“心中有剑”的境界,发展空间直觉。
2.注重学以致用,提高问题意识
图形变换法在几何教学中具有重要的价值,教师应鼓励学生学以致用,感悟图形变换的本质,创新运用图形变换的原理解决几何问题。
(1)抓住变换实质,突破解题关键
只有抓住变换的实质,才能学以致用,突破解题关键。如解决梯形问题巧用平移变换,把分散的条件通过“割补”集中在一起解决问题。
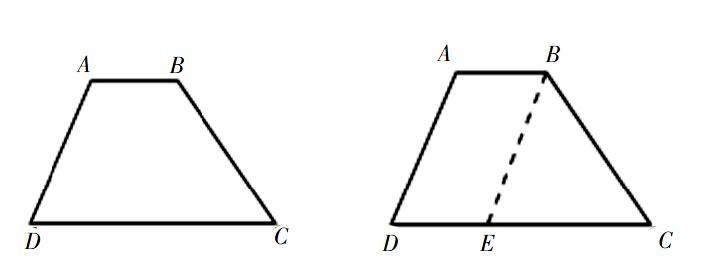
案例1:如图,梯形ABCD中,AB∥CD,若AB=2,CD=8,AD=4,则腰BC的取值范围是______[2].
设计意图:平移腰AD,把分散的条件AD、CD、AB集中在同一个三角形解決问题。在解答图形面积计算、几何证明、代数式证明等问题,图形的平移变换是解题的突破口,有效将图形进行巧妙分割与组合,使得解题过程更加方便快捷。
因此,要能抓住图形变换的实质解决问题:如旋转角是解决旋转问题的突破口,依据旋转方向与角度的关系,构造全等三角形或相似三角形解决问题;解决折叠变换问题抓住轴对称实质; 相似比是解相似问题的关键等。
(2)发挥网格作用,精准图形变换
利用网格或坐标系精准图形变换,具有很强的可操作性,“数形结合”理解变换实质。
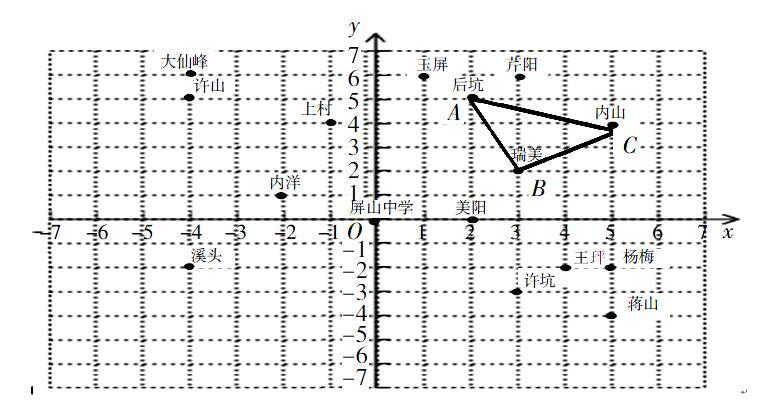
案例:如图依据本地各村庄分布建立的坐标系xoy中,△ABC为格点三角形,点A的坐标是(2,5),思考:
①将△ABC沿水平方向或竖直方向平移n个单位长度,观察对应点的坐标变化;②分别画出△ABC以y轴为对称轴进行轴对称变换,及绕点B逆时针旋转90°后的图形。
设计意图:依据各村庄分布建立坐标系进行图形变换,场景熟悉,加深对变换实质的理解。学生依据图形确定关键点,找出对应点的变换规律,是图形变换作图最常用的方法。
(3)应用图形变换,巧解几何问题
借助图形变换解决最值问题:利用图形变换优化图形结构,整合图形信息,创造性地解决复杂几何问题。如在解决几条线段和的最小值问题时,应用常规解法找不到解题突破口,而灵活应用图形变换,就会把问题转化为熟知的数学模型。
案例:如图,点M、N分别是菱形ABCD边AB、BC的中点,对角线长分别为2和3,点P是对角线AC上一个动点,求PM+PN的最小值___________[3].
设计意图:求最短路径问题,往往利用轴对称变换,PM、PN不在同一直线上,如能利用轴对称的性质转换PM(或PN)的位置,把PM翻转到PE,求两条线段PM+PN最小值就轉化为求一条线段EN最小值。教学中,通过对等腰三角形、特殊四边形等一类问题的分析讲解,引导学生从运动角度分析问题,用图形变换的思想解决问题。
利用图形变换求解图形面积:求不规则图形的周长和面积难以直接用公式计算,如能利用图形变换,通过割补、剪拼等方法转化为规则图形,就能化繁为简,解决问题。如利用平移变换巧移位,有时用旋转变换巧拼接,或用轴对称变换化零为整,只有抓住图形变换的本质,才能让图形变换在解题中发挥重要的作用。
三、感悟与反思
1.“核心素养”下应关注图形变换过程,发展空间观念
基于数学核心素养,应注重图形变换过程,在观察、比较中发现图形运动规律,获得准确的体验,由“眼中有图”过渡到“脑中有图”,建立表象,学会想象。学生在“试一试”中感受知识的形成,在“想一想”中发现运动的本质,在“说一说”中找到解决问题的途径[4],发展合情推理和思维想象能力,渗透转化与数形结合思想,发展空间观念。
2.“核心素养”下应注重解决数学问题,培养数学思维
“核心素养”下的课堂要优化练习设计,强化思维变换与探究,提高学生的解题能力与思维探究能力。学生在解题中有数学建模的思路,这是解题方法的沉淀,其实就是数学核心素养。教师要加强对图形变换方法的引导,强化解题能力,形成技能,触摸数学核心思想。
3.“核心素养”下应注重总结反思,知识再生成
“核心素养”下的课堂应注重总结反思,教材再建构,知识再生成:是否活用教材,挖掘生活中的素材进行教学;是否给学生合作探究,展示才华的机会,满足多样化的学习需求;概念的学习是否出现认识错误或理解偏颇,课例的展现是否通俗易懂,培养学生的发散思维;是否优化练习设计,满足不同层次学生的需要;在操作探究中是否发展学生的空间观念,激发学习兴趣;是否引导学生用数学语言表达图形变换的过程,培养有条理的表达能力等。
综上所述,图形变换是空间思维能力训练的最佳思维体操,图形变换教学在初中数学教学中是十分重要的,教师要引导学生从生活实例出发,从不同角度探索图形变换的特征,将学生散乱、感性的知识系统化、理性化,实现知识间的融会贯通,发展空间观念。
参考文献:
[1]潘自兴.浅谈初中阶段图形变换教学[J].福建基础教育研究,2009(11).
[2]张海燕.“四边形”复习专题[J].初中生世界,2016(6).
[3]高书生.有关四边形问题例析[J].中学生数理化(教与学),2011(3).
[4]徐宏臻.新版的“平移、旋转和轴对称”究竟该怎么教[J].新课程研究(上旬),2016(11).
