基于加速老化和实测载荷的立式贮存固体发动机药柱寿命评估

王鑫， 赵汝岩， 卢洪义， 刘磊， 伍鹏

(1.海军航空大学， 山东 烟台 264001; 2.南昌航空大学， 江西 南昌 330063)

0 引言

固体发动机寿命主要取决于药柱的贮存寿命，开展药柱寿命评估研究对于确保导弹可靠性和正常发射具有十分重要意义[1]。国内外各国都非常注重发动机贮存寿命的研究与评估工作，以美国为例，早在20世纪70年代，美国就针对老化趋势制定了长期监测计划，并于21世纪初探索监测与数值仿真技术相结合，试图实现寿命的在线分析[2-3]。同时国内外也有大量学者对推进剂寿命进行了研究，多以加速老化试验为主。Michael[4]和Bilgin等[5]分别从温度和湿度角度出发，开展不同条件下的老化试验，建立了老化程度与推进剂贮存温度之间的关系，测试了推进剂的力学性能。傅惠民等[6]和陈海建等[7]在传统Arrhenius公式基础上，分别提出改进方法，提高了预估精度。张晓军等[8]对发动机粘接界面进行了加速老化试验，测试了粘接界面的扯离强度，预测了发动机使用寿命。

以上推进剂寿命预估研究大都是通过加速老化试验，并没有考虑发动机实际承载过程，对于载荷经历越复杂的发动机，其寿命预估结果将越不准确。基于此，袁端才等[9]、谢振波等[10]和杨继坤等[11]相继开展了推进剂加速老化试验和不同贮存期的发动机点火发射过程数值仿真，基于获得的延伸率和应变随时间变化规律进行对比分析，得到了发动机贮存寿命。唐国金等[12]和高鸣等[13]进行了发动机常温点火发射下的响应面随机有限元分析，并利用应力- 强度干涉模型得到了可靠度与贮存时间的关系，进而获取发动机寿命。与此同时，Yilmaz等[14]考虑长时贮存和公路运输的影响，采用响应面法建立了应力- 应变的替代数学模型，计算了某置信区间内的瞬时可靠性。王永帅等[15]和张波等[16]还针对舰载立式贮存固体发动机药柱和粘接界面的蠕变和疲劳损伤分别展开了研究，为舰载发动机寿命评估提供了一定依据。

但上述文献未对发动机前期贮存历程展开研究，或者考虑并不全面。对于固体发动机而言，其全寿命周期需经受固化降温、公路运输、卧式贮存和战备值班以及最终的点火发射过程，固化降温使发动机药柱产生不可忽视的预应力和预应变，公路运输产生的随机振动载荷使药柱产生累积损伤，战备值班长时立式贮存以及周期性的低频振动载荷会使药柱产生不可恢复的蠕变与疲劳损伤，这些因素都将影响后续的点火发射，也影响着发动机寿命。

本文忽略卧式贮存及公路运输载荷的影响，并在通过高温加速老化试验获取延伸率随时间变化规律的基础上，开展不同贮存期发动机经固化降温、立式贮存及点火发射的数值仿真，获取点火增压和弹射过载联合作用下的药柱最大von Mises应变。同时开展实测振动载荷下发动机的有限元分析，计算发动机动态立式贮存半年时间的疲劳损伤。进而通过延伸率和应变的变化规律，结合疲劳损伤值预估贮存温度下发动机寿命，并得到了发动机前期贮存时间与动态立式贮存次数的关系式。

1 加速老化试验

本文所选材料为某型固体火箭发动机药柱所用的端羟基聚丁二烯(HTPB)复合推进剂。根据航天工业部标准QJ2328A—2005《复合固体推进剂高温加速老化试验方法》、QJ1615—89《复合固体推进剂单向拉伸试验方法》以及QJ2487—93《复合固体推进剂单向拉伸应力松弛试验及主曲线测定方法》，选取50 ℃、60 ℃和70 ℃ 3个温度进行加速老化试验，选取不同测点获取推进剂各参数随老化时间的变化规律。

图1 最大延伸率变化趋势Fig.1 Changing curves of maximum extensibility

最大延伸率δm和最大抗拉强度σm结果如图1和图2所示，其中t为老化时间。由图1和图2可见：随着老化时间增加，推进剂逐渐变硬，呈现抗拉强度和模量不断增加，延伸率不断减小的趋势；同时随着温度升高，变化趋势加快。

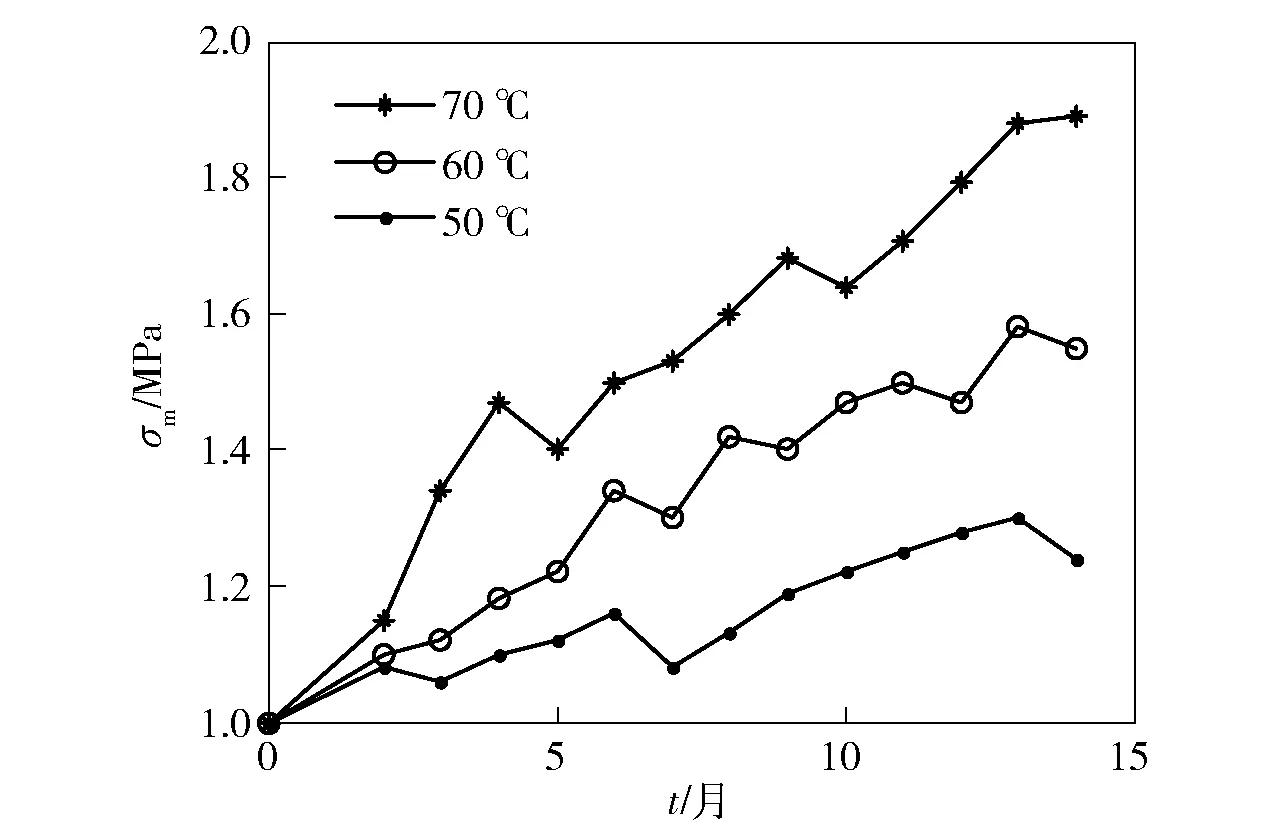
图2 最大抗拉强度变化趋势Fig.2 Changing curves of maximum tensile strength

通常，加速老化性能δm随时间的变化规律可用以下3种模型进行表示，其分别记作模型1、模型2和模型3.

δm=δ0+Klgt,

(1)

δm=δ0+Kt,

(2)

δm=δ0exp (-Kt),

(3)

式中：δ0为常数；

K=Zexp (-E/(RT))，

(4)

Z为频率因子，E为表观活化能，R为气体常数，T为热力学温度。

表1列出了试验数据对各模型的拟合结果，其中δ1、δ2和δ3以及K1、K2和K3为拟合参数，r1、r2和r3为相关系数。

表1 各模型拟合结果

由表1可知，3个模型拟合结果都比较好，故选用较为简单的线性模型作为最终拟合结果。根据《复合固体推进剂高温加速老化试验方法》标准中数据处理方法，通过(2)式和(4)式推导出贮存温度Ts(Ts=20 ℃)条件下推进剂最大延伸率δm的变化规律为

δm=60.4-exp (29.633 3-9 361/Ts)×t.

(5)

2 三维有限元分析

2.1 模型建立及材料参数

某型固体发动机药柱为带有前后人工脱粘层的前后翼槽结构，具有几何对称性，模型结构及网格划分如图3所示。

图3 发动机模型结构及网格划分Fig.3 Structure and mesh generation of motor model

通过推进剂松弛试验获取其松弛模量E(t)主曲线，并用Prony级数形式表示，仅给出未老化推进剂在20 ℃下松弛模量主曲线表达式，如(6)式所示，老化试件松弛模量获取方法同未老化试件。同时将各部件主要参数列于表2中。

E(t)=1.037+3.26e-t/0.04+2.068e-t/0.4+1.284e-t/4+
0.891e-t/40+0.587e-t/400+0.43e-t/400+0.316e-t/40 000.

(6)

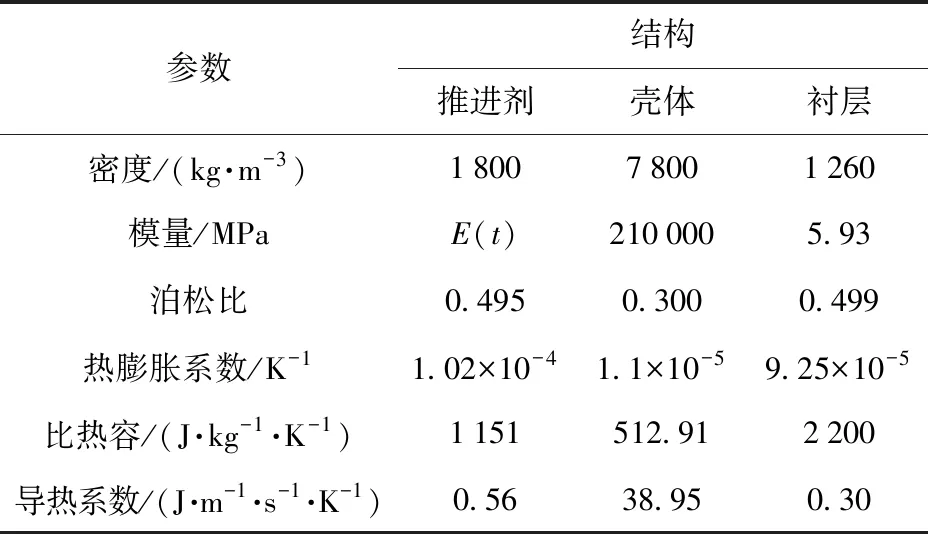
表2 各部件材料参数

2.2 边界及载荷处理

在仿真过程中主要考虑固化降温载荷、立式贮存载荷以及点火发射与弹射增压载荷，忽略其他载荷对发动机寿命的影响，并分别开展以下工况的有限元仿真，工况如表3所示。其中：工况1的运算可以获取药柱经联合载荷作用下的最大von Mises应变发生位置；通过工况2中对立式贮存时间(立式贮存次数)的调整，探寻贮存寿命与立式贮存次数之间的关系；通过工况3计算药柱在立式振动载荷条件下的疲劳损伤，最终得出发动机经表3所示5种载荷综合作用下的贮存寿命。

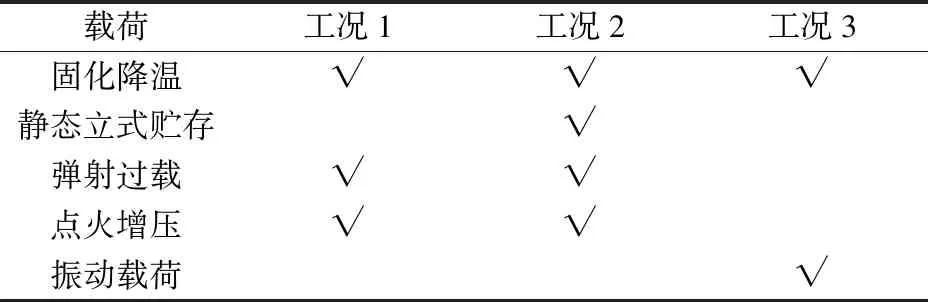
表3 各工况对应载荷历程

在工程模拟有限元软件Abaqus中，通过设置多个分析步来实现不同工况下联合载荷的仿真计算，且后一载荷工况在前一载荷的仿真结果基础上进行，并通过改变药柱模量参数来实现推进剂老化因素的关联。

表3中：固化降温过程的0应力温度为50 ℃，经过一段时间降至室温；静态立式贮存过程中恒定承受1g的重力载荷，长时立式贮存时对药柱施加前期拟合的蠕变参数，即

(7)

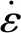
同时为简便计算，将弹射过载与点火增压载荷认定为线性载荷；振动载荷采用实际监测数据，选取具有代表性的100 s进行计算。前两种工况由于边界及载荷的对称性，仿真对象选用1/16模型；由于工况3中振动载荷由横摇、纵摇及垂荡3个方向的加速度共同决定，仿真对象选用全尺寸模型。

令ax、ay和az分别表示垂荡、横摇及纵摇3个方向的加速度，图4所示为经数据处理后的各方向加速度随时间变化曲线，其中ta为加速度振动载荷采集时间。

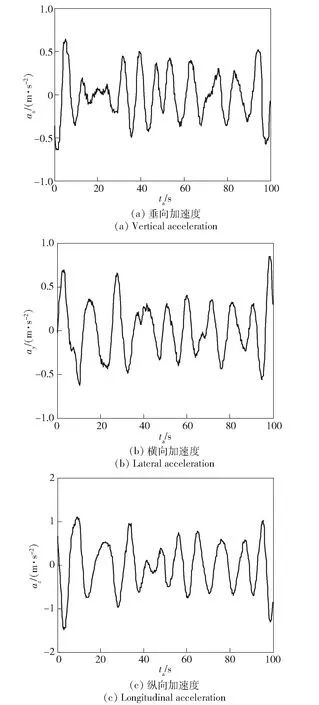
图4 3个方向实测加速度曲线Fig.4 Accelerations in three directions

2.3 仿真结果及分析

2.3.1 立式贮存

对未老化发动机的三维数值仿真结果表明：经固化降温载荷后，在热应力作用下，药柱前后人工脱粘层张开，药柱中孔扩张，药柱内部产生初始预应力与预应变；在立式贮存初期，在1g轴向重力载荷作用下，药柱前人工脱粘层继续扩张，后人工脱粘层开口距离减少，药柱整体有向尾部下沉的趋势；经长期静态立式贮存载荷后，药柱整体下沉量增大，最大位移值增大了14.82%，后人工脱粘层缝隙逐渐减小，表明药柱在长期立式贮存下会产生蠕变。发动机药柱在不同载荷下的位移历程如图5所示。由图5可见，由于位移变化占据发动机总长的比例较小，故为清晰看清药柱在各阶段变形趋势，图5为放大15倍之后的结果。

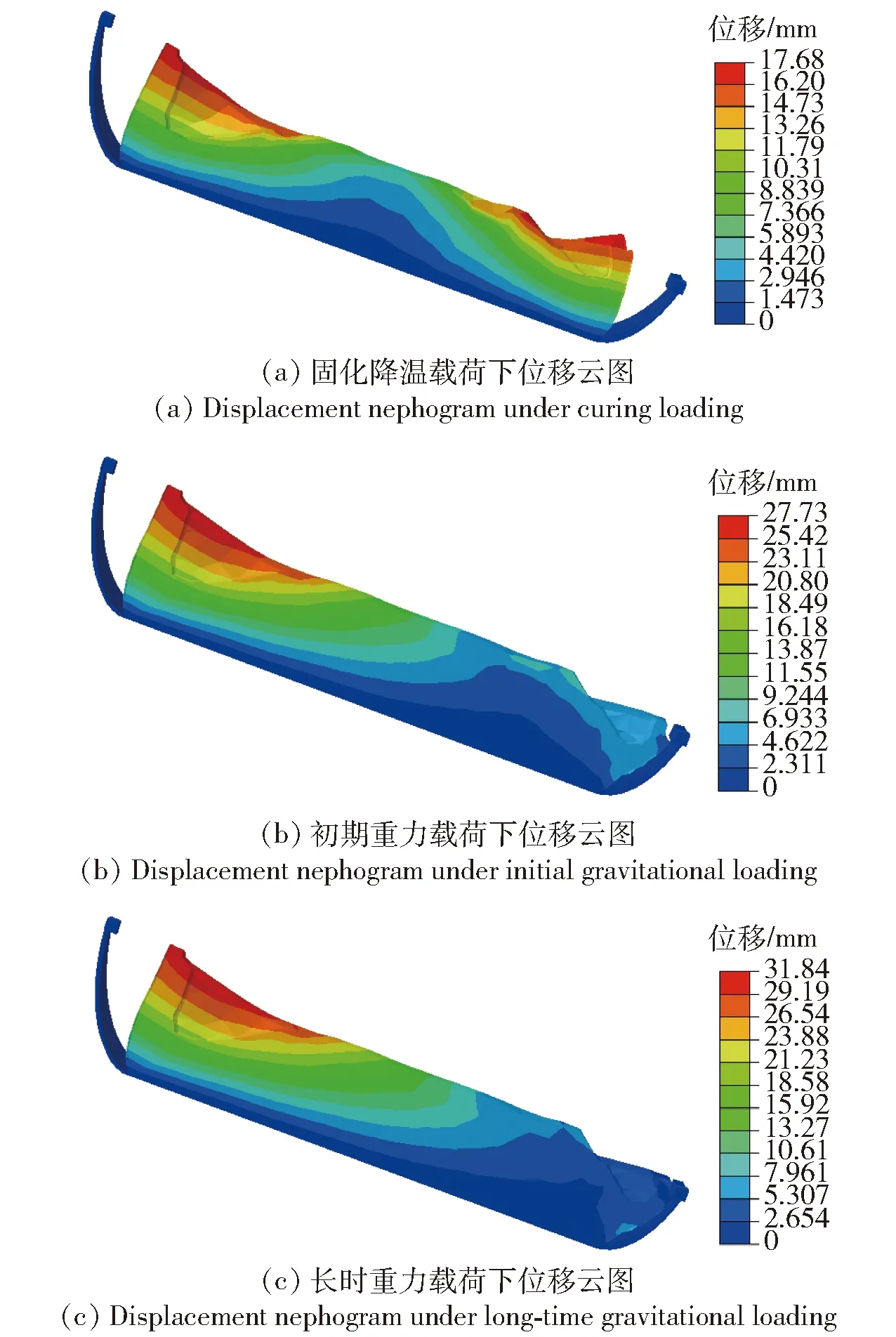
图5 立式贮存下不同阶段位移变化云图Fig.5 Displacement nephograms at different phases during vertical storage

图6为长时立式贮存后的药柱应变云图，最大应变发生在药柱前翼与中孔交汇位置，可达0.042 37.

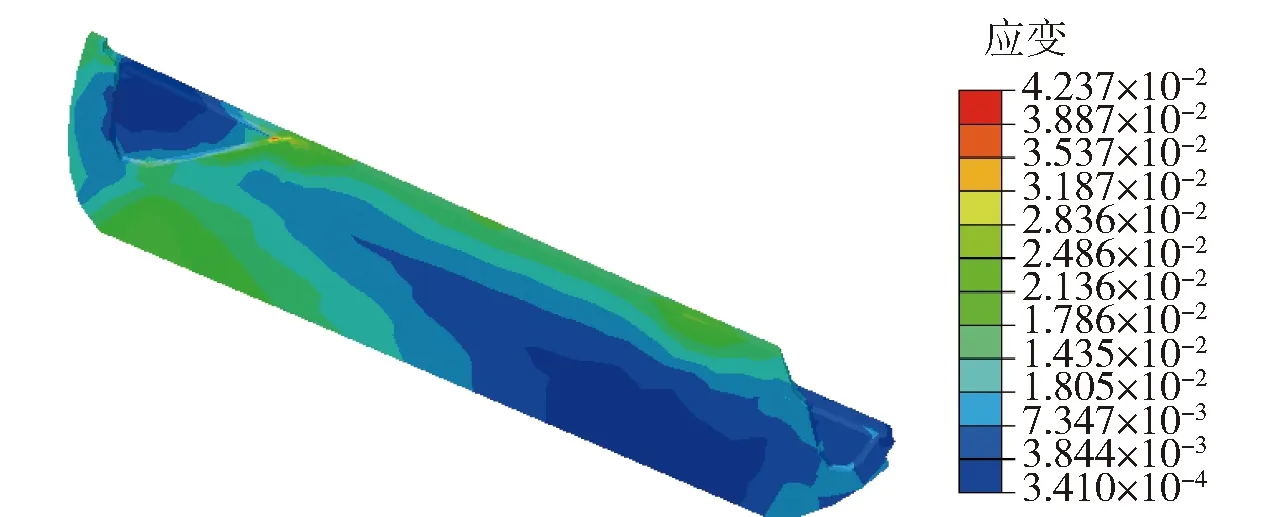
图6 长时立式贮存后应变云图Fig.6 Strain nephogram after long-time vertical storage

2.3.2 点火增压和弹射过载

在远大于重力加速度的弹射过载和点火增压载荷联合作用下，药柱前后人工脱粘层与前后封头贴紧，位移分布如图7(a)所示。应变分布发生变化，最大von Mises应变值出现在前翼槽附近，比贮存阶段增大了10倍，危险点记为点A，如图7(b)所示。

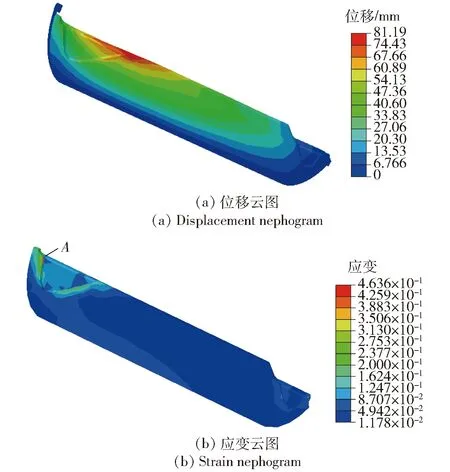
图7 点火增压和轴向过载仿真云图Fig.7 Simulation nephograms under inner pressure and axial acceleration loadings

2.3.3 振动载荷

在进行固化降温和实测振动载荷联合作用下的数值仿真时，对ax方向施加重力载荷。图8给出31.4 s(某一应力幅值)时药柱外部和内部的应力分布结果，药柱前翼及中孔处存在较明显的应力集中。

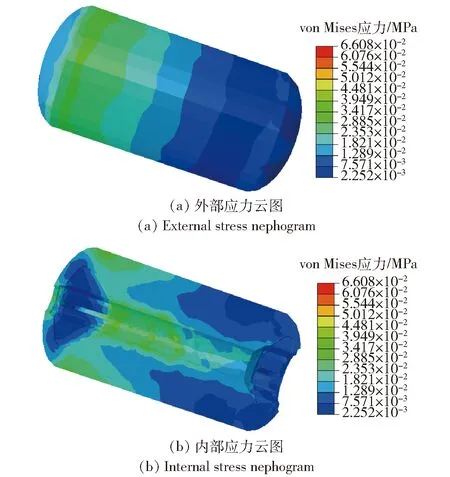
图8 振动载荷仿真云图Fig.8 Simulation nephograms under vibration load

发动机药柱在该时间点最大von Mises应力σvM值为0.066 08 MPa，远小于推进剂的最大抗拉强度值，因此在周期性振动载荷下药柱不会发生瞬时失效，但是周期性运动产生的累积疲劳损伤不可忽视。虽然结果表明药柱中孔应力值较大，但计算发现其最大应力幅值为0.5 kPa，远小于药柱点火载荷对应的危险点A的应力幅值，因此以点A对应的应力变化趋势作为药柱累积损伤的计算依据，该点最大应力幅值在1.2 kPa左右，应力变化具有明显的周期性，如图9所示。

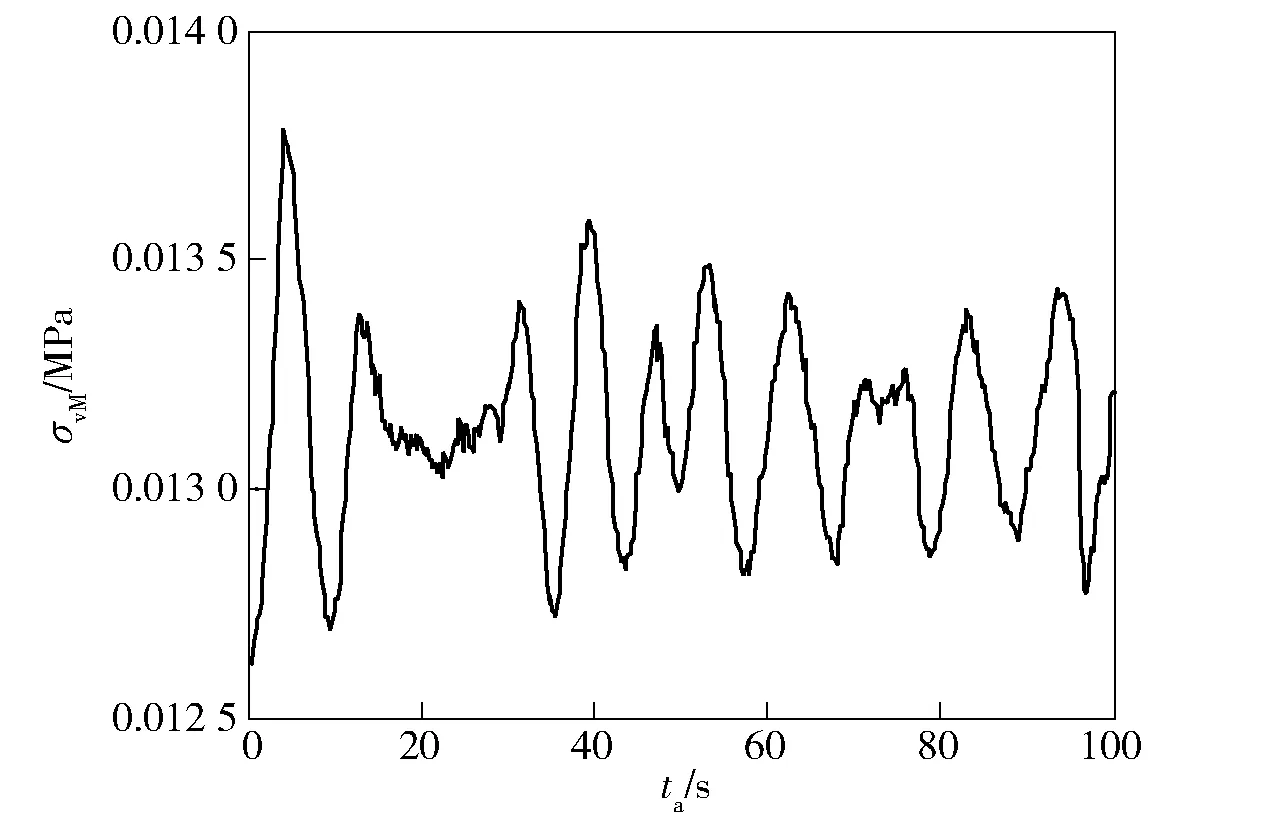
图9 药柱危险点应力变化规律Fig.9 Variation of stress of grain dangerous point

3 发动机药柱贮存寿命评估

3.1 基于化学老化和立式贮存的发动机寿命评估

在前期对各工况进行数值模拟的基础上，对工况2中立式贮存时间进行调整，以半年作为一次立式贮存周期，仿真过程中考虑不同贮存温度和不同贮存老化时间的发动机药柱模量变化，考虑立式贮存过程中的老化因素，忽略其他参数的影响，得到发动机经历不同立式贮存次数下进行点火发射的仿真结果。经仿真发现，发动机经不同老化时间和静态立式贮存时间后进行点火发射时，药柱危险点位置并未发生变化。根据(5)式的推导方法，得出常温下危险点von Mises应变εvM随时间的变化规律。以工况2为例，点火之前经历了半年时间的静态立式贮存，考虑20%的富裕量[9]，应变表达式为

εvM=0.548 8-exp (6.921 8-2 841.2/Ts)×t.

(8)

最大von Mises应变εvM与老化试验所得到的延伸率δm共同绘制于图10中，在交点O处有εvM=δm成立，交点横坐标th表示药柱在立式贮存之前自然贮存老化的时间，即卧式贮存时间。若εvM<δm，则表明贮存多年后，发动机经历固化降温、静态立贮后点火发射时产生的最大应变值小于推进剂贮存后的最大延伸率；若εvM>δm，则结果反之。因此，认为发动机卧式贮存th后历经工况2的载荷后满足结构完整性要求。将发动机立式贮存时间定义为tv，认为th与tv之和为发动机总的贮存寿命ttot.

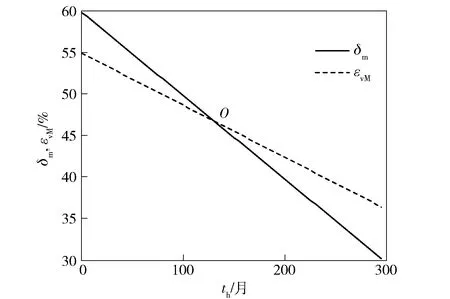
图10 应变和延伸率随时间变化规律Fig.10 Variation of strain and extensibility with time

在该工况下，th为132.2个月，即11.02年，因此ttot=11.52年。该参数同时也表明，若发动机卧式贮存时间超过11.02年，则其无法完成1次静态立式贮存。

3.2 考虑振动载荷的发动机寿命评估

通过雨流计数法对应力变化历程进行计数，进而利用Miner线性损伤理论和前期拟合的推进剂疲劳本构方程计算药柱危险点的疲劳损伤[17]。疲劳本构方程见(9)式：

lgn=8.073 3-7.800 3σ，

(9)

式中：n为推进剂的疲劳破坏次数；σ为往复拉伸试验的应力幅值。

图11表示100 s内应力雨流计数结果，其中C-D和C-U分别表示具有下降趋势和上升趋势的全循环，HC-D和HC-U分别表示具有下降趋势和上升趋势的半循环，图11中共计10个全循环和5个半循环。计算得到药柱动态立式贮存半年的累计损伤为0.017 12，损伤随着贮存时间线性增加。

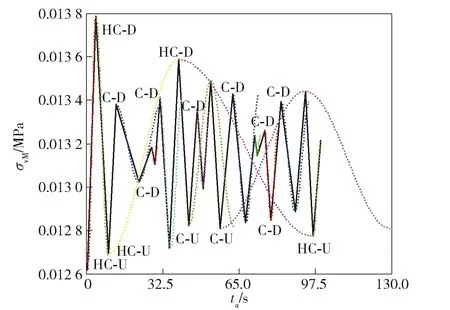
图11 雨流计数结果Fig.11 Result of rainflow counting

以前述工况为例，考虑振动载荷下的药柱疲劳损伤计算结果，th进一步减小，降低至129.9个月，即10.83年，发动机寿命为ttot=11.33年。表明若发动机卧式贮存时间超过10.83年，则其无法完成1次动态立式贮存。

3.3 卧式贮存时间与立式贮存次数的关系

为了探究立式贮存时间与发动机卧式贮存时间的关系，开展不同长时立式贮存期的发动机数值仿真。由于装药在立式贮存过程中也受老化影响，延伸率随着贮存时间呈线性减小的趋势。在0～20次内选择6种贮存工况分别进行计算，由于计算结果较为密集，仅列出立式贮存0次和10次时的计算结果如图12所示，A、B两点分别对应两种工况下th值。

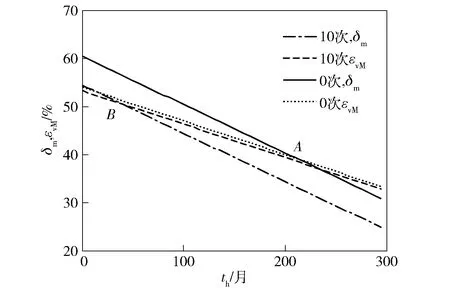
图12 不同立式贮存期下应变变化规律Fig.12 Variation of strain in different vertical storage times

令N表示动态立式贮存次数，图13表示th值与N之间的关系。由图13可见：随着立式贮存时间tv的增加，发动机卧式贮存时间th呈减小趋势，且变化率逐渐衰减；反之，随着发动机卧式贮存时间th的延长，发动机后期可允许的立式贮存次数N将逐渐减小。

图13 N与th之间的关系Fig.13 N vs. th

卧式贮存时间与立式贮存次数之间的关系进行拟合，将考虑到发动机从出厂至交付存在一定的时间间隔，因此th=0的情况并不存在，考虑可以用(10)式的形式来描述二者之间的关系，相关系数为96.37%，将拟合结果也绘制于图13中。

th,min=193.3e-0.24×N.

(10)

在这里，取th,min=5月，故Nmax=15次。

ttot受th,min和N的影响，图14表示发动机总贮存寿命ttot随N的变化规律，随着N的增加，发动机受老化因素和立式蠕变影响，总寿命呈减小趋势，且变化逐渐缓慢，采用(11)式表述二者之间的关系。

ttot=9.576e-0.781 6N+8.237.

(11)

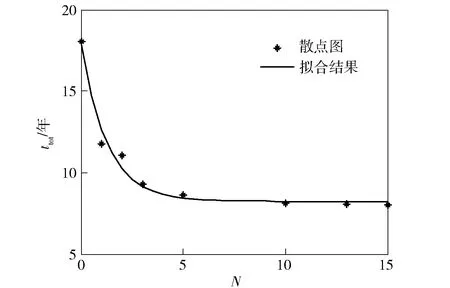
图14 ttot随N变化关系Fig.14 ttot vs. N

最后得出发动机总贮存寿命变化规律，考虑立式贮存时，发动机总贮存寿命介于8.24～11.75年；不考虑立式贮存时，发动机总寿命为17.81年。从结果看，立式贮存下总寿命比卧式贮存减小34.0%～53.7%，因此应对发动机立式贮存状态引起高度重视，并应根据实际贮存情况规划立式贮存方案。

4 结论

本文基于加速老化试验和实测振动载荷对发动机进行了三维建模与数值仿真，预估了发动机寿命，并得出了卧式贮存时间与动态立式贮存次数之间的关系。得出主要结论如下：

1) 通过推进剂50 ℃、60 ℃和70 ℃ 3个温度下的加速老化试验，得出了推进剂在常温下延伸率与贮存时间的关系式δm=60.4-exp (29.633 3-9 361/Ts)×t.

2) 有限元分析表明：在固化降温和重力作用下，发动机前后人工脱粘层张开，药柱整体向尾部下沉；受蠕变影响，随着贮存时间的增加，药柱变形量缓慢增大。之后进行点火发射，药柱最大von Mises应变值急剧增加，发生在药柱前翼槽。

3) 在固化降温和实测振动载荷的联合作用下，药柱内部各点产生周期性的应力。药柱危险点最大应力幅值在1.2 kPa左右，大于中孔及尾部应力幅值，药柱动态立式贮存半年时间的累积损伤为0.017 12.

4) 对不同立式贮存时间下的发动机进行点火发射，将最大von Mises应变与延伸率进行比较，进而加之疲劳损伤，得出贮存寿命随动态立式贮存次数的变化规律。随着发动机贮存时间的增加，其允许立式贮存次数相应减少。

5) 推导动态立式贮存次数与卧式贮存时间之间的关系式为th=193.3e-0.24×N，同时给出最大立式贮存次数为15次，发动机总贮存寿命随着立式贮存次数逐渐减小，介于8.24～17.81年之间。

6) 粘接界面发生破坏也是固体发动机的主要失效模式，后续应对粘接界面在联合工况下的损伤及结构破坏展开深入研究。