摇臂悬挂机动平台运动姿态调节最优控制研究
2019-12-23韩子勇苑士华裴伟亚李雪原周俊杰
韩子勇, 苑士华, 裴伟亚, 李雪原, 周俊杰
(1.北京理工大学 车辆传动国家重点实验室, 北京 100081; 2.徐工集团 江苏徐州工程机械研究院, 江苏 徐州 221004)
0 引言
非结构化环境下越野车辆或者移动机器人的运动方式,通常分为轮式、腿式、履带式和混合式[1],摇臂悬挂机动平台作为一种轮腿复合并联空间移动机构,综合了腿式和轮式移动机构的优势,具有高机动性、高通过性和高稳定性特点,受到国内外学者的广泛关注。在“跨越险阻2018”山地机动和极限越障考核项目中,出现了许多轮腿构型车辆并取得了较好的成绩。
对比传统轮式车辆,轮腿复合移动车辆通过调节运动姿态提升了对非结构化环境的适应能力,但同时也存在系统机构不稳定和运动控制复杂的难点。Grand等[2-3]利用机器人逆运动学模型实现了运动姿态和质心轨迹的解耦控制,并对车辆在斜坡上的梯度稳定裕度和轮地接触点的垂向载荷进行了离线优化。Thomson等[4]使用相同的逆运动学控制方法实现了液压驱动轮腿机器人的姿态控制,并对驱动关节的力矩进行了在线优化。Suzumura等[5]利用基于运动学约束的分解动量控制方法实现了轮腿机器人的质心轨迹和运动姿态控制,同时利用零力矩点模型解决了防倾覆的稳定性控制问题。Grand等[6]以摩擦圆约束为目标函数,以整车动力学平衡和关节力矩限制为约束,建立了一种在线的线性规划运动控制优化方法,但是该优化控制方法只能适用于求解特定障碍工况下质心轨迹和地面反作用力的分布。Morihiro等[7]提出了一种基于机器人逆运动学模型和静力学平衡的模型预测控制方法,依据预测的地面约束和载荷分布优化了轮腿轨迹。Castano等[8]使用基于逆运动学模型的二次规划优化控制方法,完成了机器人的姿态平衡控制。Yool等[9]将轮腿混合机器人(LWHR)地面反作用力和质心广义力之间的映射矩阵分解变换为带输出约束的线性可逆映射矩阵和遵循动量守恒的线性映射矩阵,实现了对地面反作用力的直接控制,但是这种方法的计算量大,控制方法的实时性受到限制。在国内,孙鹏飞[10]分析了典型障碍下的运动姿态,运用运动学模型基础,以质心稳定裕度、越障裕度等为目标函数,对整车运动姿态进行了优化仿真。石米娜[11]利用整车运动学约束控制模型,对垂直障碍、壕沟、攀爬和转向等工况下各驱动单元的运动协调控制进行了研究。王红梅[12]实现了轮腿机器人轨迹跟踪、滑转率、姿态稳定和越障功能的分层协调控制,在其位姿控制器中使用的是运动学模型。Niu等[13]利用旋量理论建立了机器人运动学模型,并进行了位置分析和运动轨迹规划。
综上所述,由于轮腿复合移动车辆自身机构运动自由度多、控制复杂的特性,其运动控制以运动学控制为主,在特殊工况下甚至只控制质心轨迹忽略运动姿态的调节,从而不能准确描述复杂环境中驱动关节的力矩与质心轨迹和姿态运动之间的关系,进而影响了对质心轨迹和运动姿态调节的动态控制。因此,本文结合质心动力学模型和二次规划方法,提出一种兼顾系统动力学平衡和轮地相互作用力约束的动力学优化控制方法,实现对轮腿复合移动车辆运动姿态的动态实时优化控制,并通过仿真对侧倾和俯仰等运动姿态的调节进行了验证。本文研究目的与文献[9]近似,均期望通过对地面反作用力的直接控制实现对整车运动姿态的调节,但区别在于对欠定方程求解的处理方式不同:文献[9]的矩阵分解法需要针对控制对象建立输出约束且矩阵分解计算量大,其通用性和实时性受到限制;本文将求解问题转化为范数最小化问题求优化解,并验证了方法的通用性和实时性。
1 摇臂悬挂机动平台
摇臂悬挂机动平台整车为18自由度轮腿复合移动车辆,其中车体具有5个可控自由度,在行驶、转向基础上增加了对垂向、侧倾和俯仰的运动控制,使得整车对复杂不规则地形的适应能力得以提升,能够通过独立控制并联多摇臂结构实现对复杂地形的主动越障。
整车机械结构由车体、摇臂悬挂系统和车轮构成,摇臂摆角的调节和车轮运动均为分布式独立驱动控制。整车详细结构如图1所示。
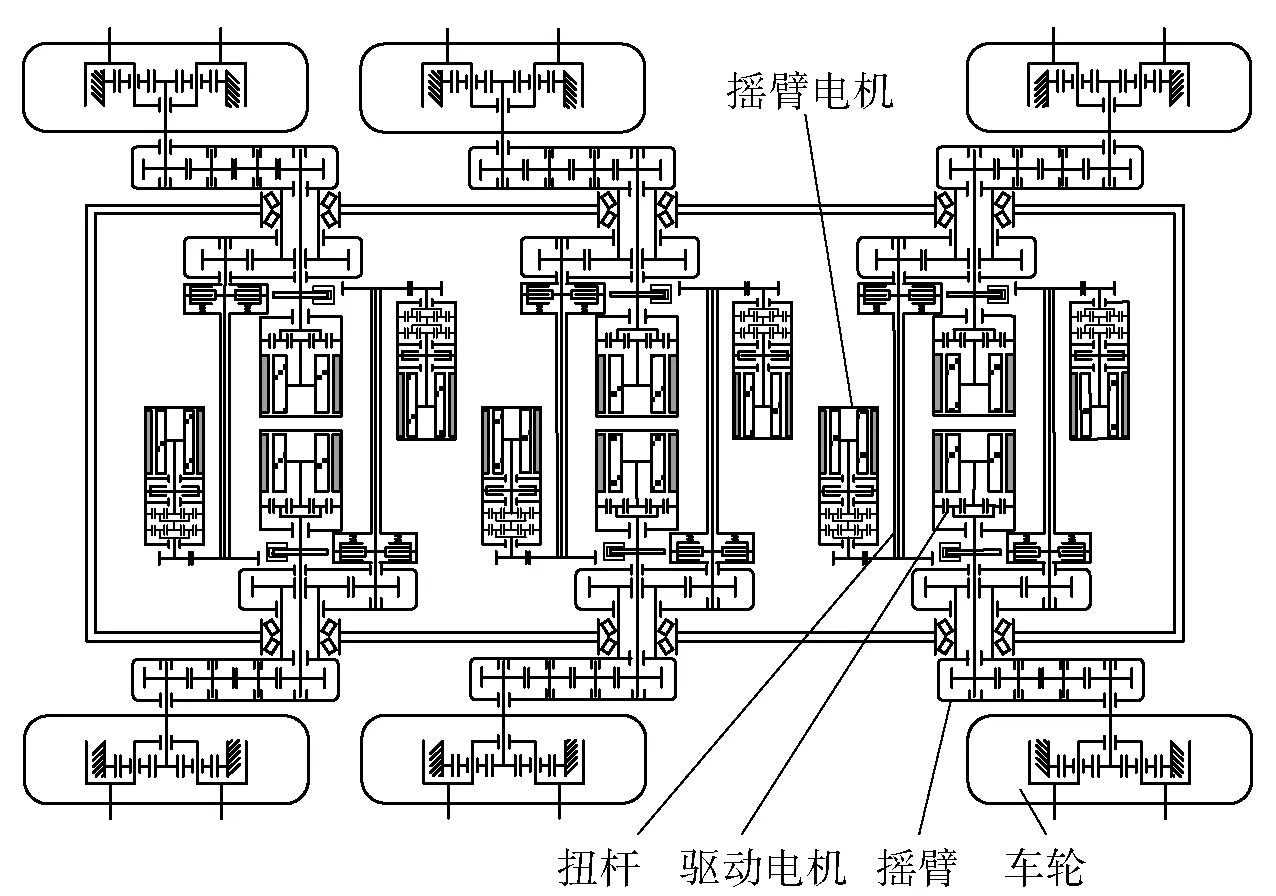
图1 整车结构布局原理图Fig.1 Schematic diagram of vehicle structure layout
2 整车控制器及地面反作用力的最优分配
决定一辆汽车如何转向、制动和加速的关键控制力产生于4块不大于人手掌大小的接触区[14],同样整车运动姿态调节所需的垂向力、纵向力和侧向力都来自于车轮和地面的相互作用力,因此合理的分配地面反作用力是整车运动姿态调节的基础。
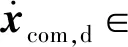
2.1 质心动力学
多体系统的质心动力学方程[15-16]描述为
(1)
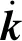
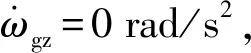
(2)
(3)
式中:fi=(fix,fiy,fiz)T∈R3为地面反作用力,fix、fiy和fiz分别为轮地接触点的纵向力、侧向力和垂向力(见图3,其中pi为轮地接触点位置向量)。
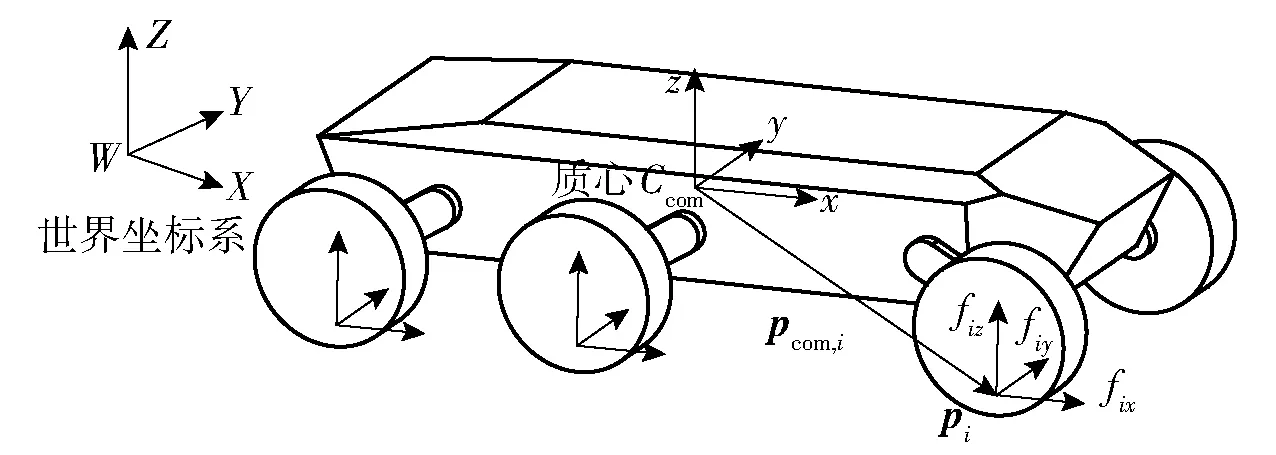
图3 坐标系设置及受力简图Fig.3 Frames arrangement and force distribution
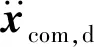
2.2 质心加速度和车体姿态角加速度
通过PD控制器质心的需求加速度计算公式为
(4)
式中:Kpl∈R3×3和Kdl∈R3×3分别为正定对角比例和微分增益矩阵。类似地,需求车体的角加速度计算公式为
(5)
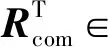
2.3 计算需求的地面反作用力
给定一个目标质心加速度和车体角加速度,可以利用以下公式计算:
(6)
式中:I∈R3×3为单位矩阵;[pcom,i]×∈R3×3表示由向量pcom,i构成的反对称矩阵;f∈R3c为车轮的地面反作用力。
(6)式由(2)式和(3)式中的加速度替换为目标加速度并改写为矩阵格式得到,其中有6个方程和3c个未知量,显然有无穷多解。通过添加由摩擦圆决定的不等式约束,可以将该问题转化为二次规划问题来求解。在控制器的每个控制周期内,都求解下述二次规划问题:
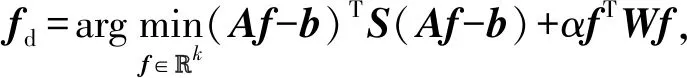
(7)
式中:S∈R6×6和W∈Rk×k(k=3c)为正定权重矩阵;α∈R为第2个优化目标的权重系数;C∈Rp×k为不等式约束矩阵,p为不等式约束个数;dub∈Rp为对应的上边界。(7)式确保了所求解的地面反作用力都在摩擦圆约束内,且反作用力的法向分量保持在自定义范围内。
车轮垂向载荷和路面摩擦系数决定了车轮附着力的大小,二者关系可以由图4(a)所示的摩擦圆锥表示,图4(a)中μ为摩擦系数。
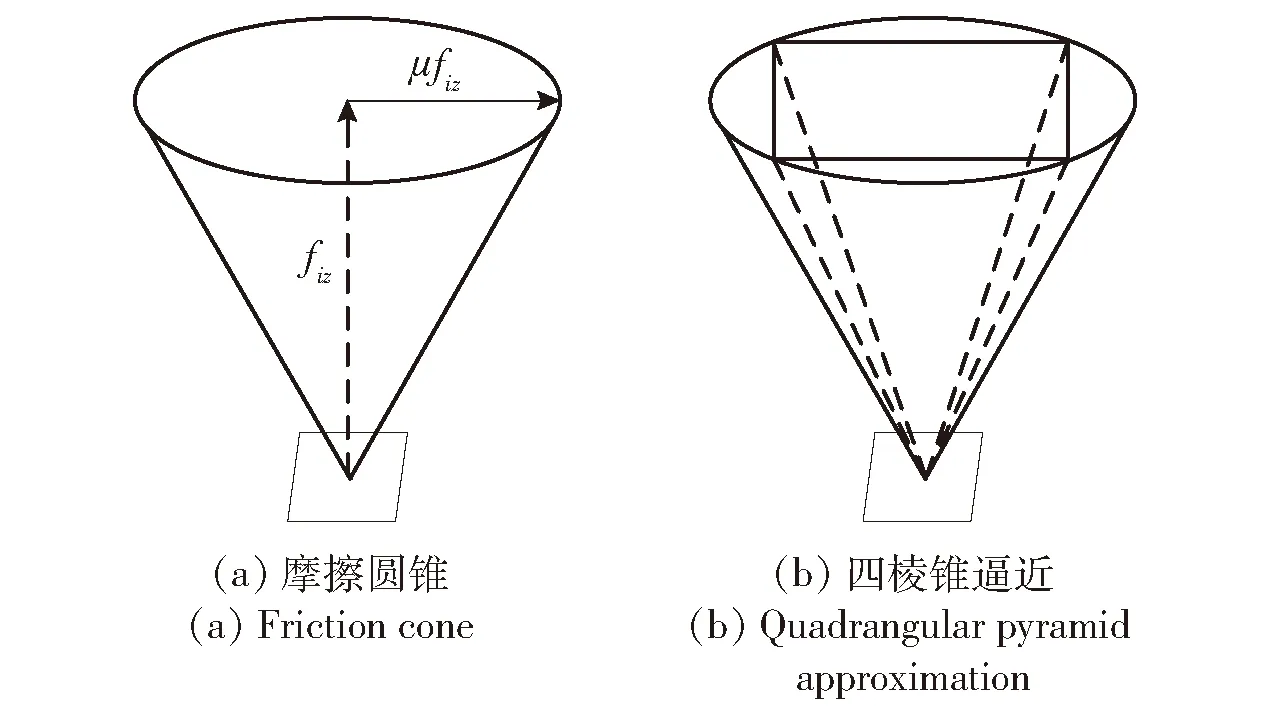
图4 地面反作用力的空间摩擦圆锥及其逼近Fig.4 Friction cone of ground reaction force and its approximation
在纯侧偏工况下,侧向力存在以下峰值约束:
‖fiy‖≤μypfiz,
(8)
式中:μyp为侧向力峰值附着系数。
在纯纵向工况下,纵向力存在以下峰值约束:
‖fix‖≤μxpfiz,
(9)
式中:μxp为纵向力峰值附着系数。
对于侧偏和纵向联合工况,摩擦圆的限制可以用(10)式表示:
(10)
式中:fixy为联合工况下的合力;μp为对应路面条件下的峰值附着系数。
由垂向载荷和摩擦圆构成的2阶圆锥约束不能直接用于二次规划,且2阶圆锥规划目前没有快速求解器[17],用一个4棱锥体来逼近摩擦圆锥,见图4(b)所示。(8)式~(10)式所决定的约束可以统一描述为
(11)
式中:fimax∈R为第i个支撑摇臂的车轮垂向载荷的最大值。
(7)式中的不等式约束矩阵C和约束边界dub定义如下:
(12)
式中:
(13)
综上所述,根据(7)式和(12)式建立了轮腿机构求解地面反作用力的通用二次规划框架:
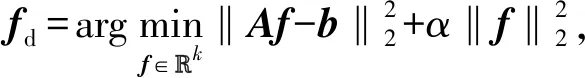
(14)
式中:优化目标的物理意义是使动力学平衡方程的残差最小,同时满足求解的地面反作用力最小;优化变量为地面反作用力f;约束条件满足用四棱锥逼近的地面摩擦约束。
2.4 地面反作用力映射为关节转矩
车辆运动姿态的调整最终通过在各驱动关节施加力矩实现。需求的关节力矩τd为
τd=τff+τfb,
(15)
式中:τff为驱动关节的前馈力矩;τfb为状态反馈力矩项。
根据机器人学力平衡与系统雅克比矩阵的映射关系[16],驱动关节前馈力矩τff的计算公式为
τff=JTfd,
(16)
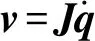
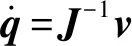
(17)
式中:PD表示使用PD控制律计算状态反馈力矩。
3 整车运动轨迹的定义
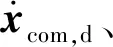
给定质心的运动轨迹后,还需要计算摇臂关节和车轮关节的目标轨迹qd,用于状态反馈力矩PD算法的目标参考。关节目标轨迹可以在确定轮地接触点pi后,由逆运动学模型计算得到。第i个摇臂轮地接触点的速度[19]为
(18)
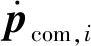
4 仿真实验
为了验证本文运动姿态调节动态优化控制方法,采用MATLAB多体动力学工具箱Simscape Multibody对所设计的运动轨迹和姿态调节优化控制算法进行仿真验证。控制器的控制目标是在跟踪目标运动轨迹的同时实现对车体运动姿态调节的控制。表1所示为仿真时使用的PD控制律和优化变量权重参数设置,表2所示为实际工程控制器所需的状态参数及其数据来源。仿真在CPU型号为Intel core i7-4710MQ 2.5 GHz的笔记本电脑上实现。在优化求解器的选择方面,如图5所示比较了MATLAB二次规划求解器quadprog和开源求解器qpOASES[20],二者均能满足实时控制的需求,但后者计算更快,最终选择qpOASES,计算30个不等式约束的平均时间为0.19 ms.
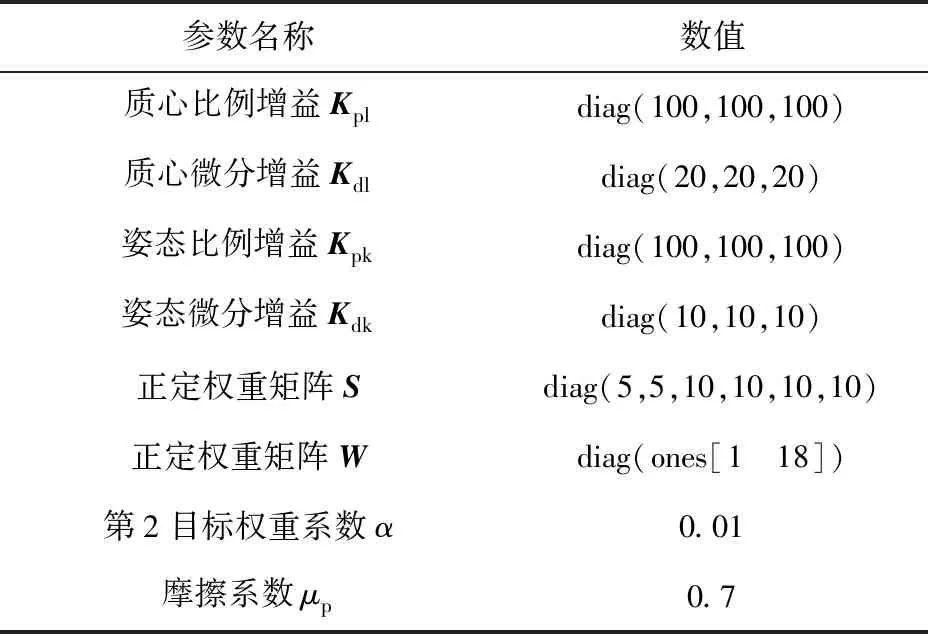
表1 优化控制器参数设置

表2 优化控制器的状态参数
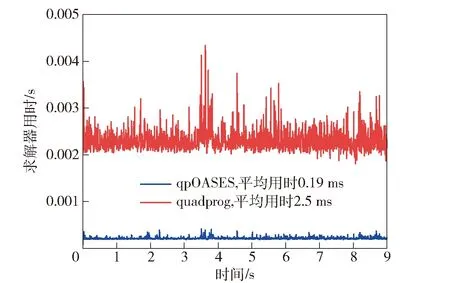
图5 二次规划求解器的CPU求解时间Fig.5 CPU usage of QP solvers
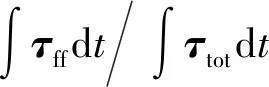
4.1 侧倾姿态
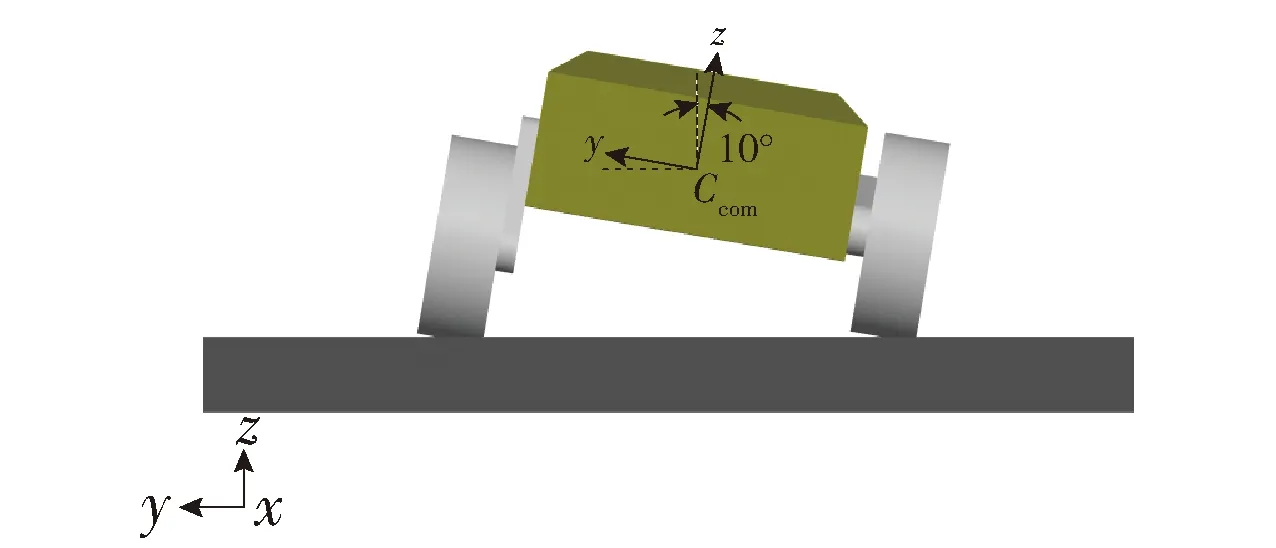
图6 绕x轴侧倾运动Fig.6 10° roll motion about x axis
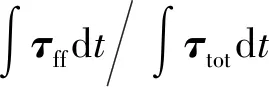
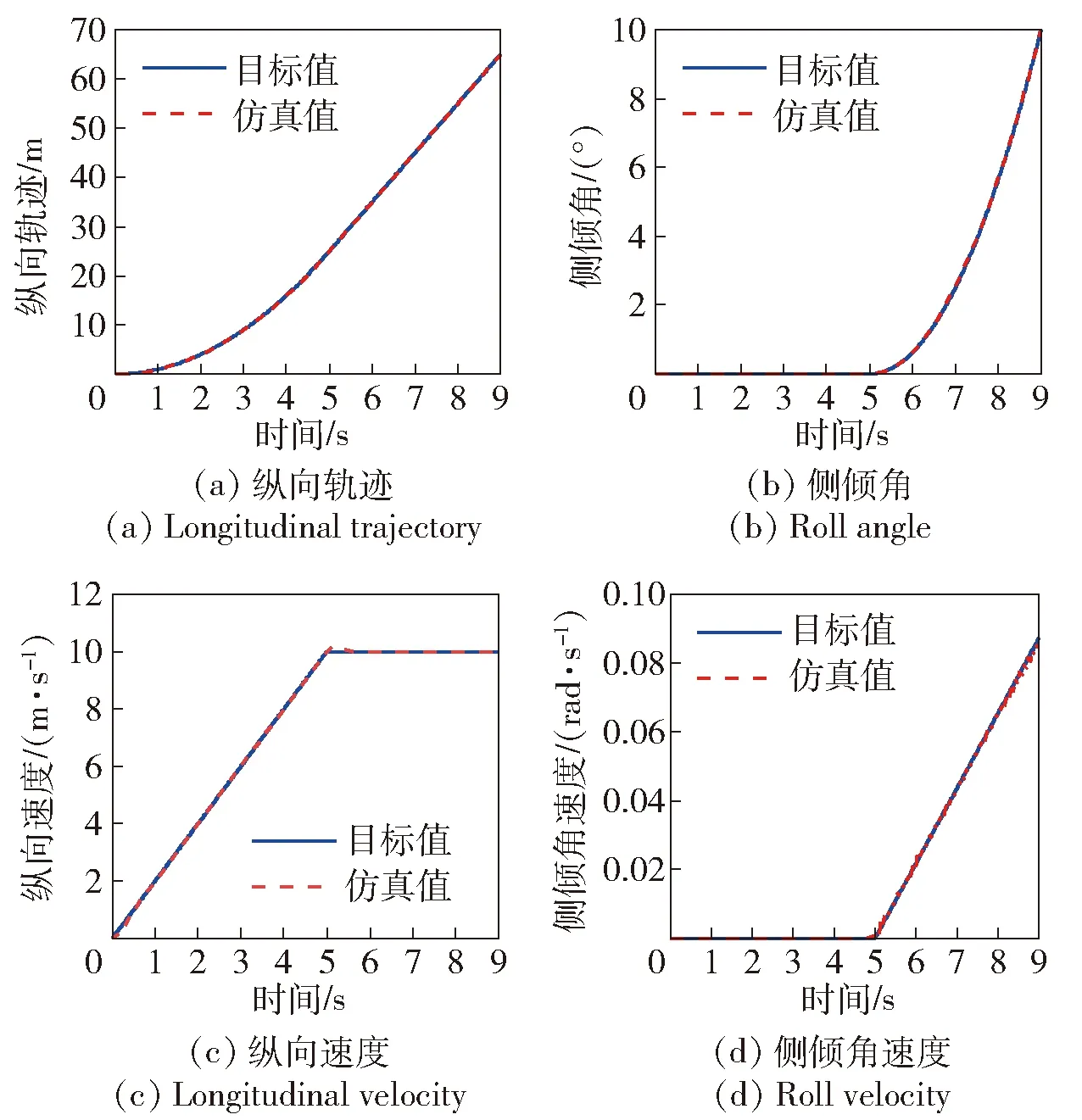
图7 整车质心和姿态运动轨迹的目标值和仿真结果Fig.7 Desired and simulated values of vehicle COM and posture
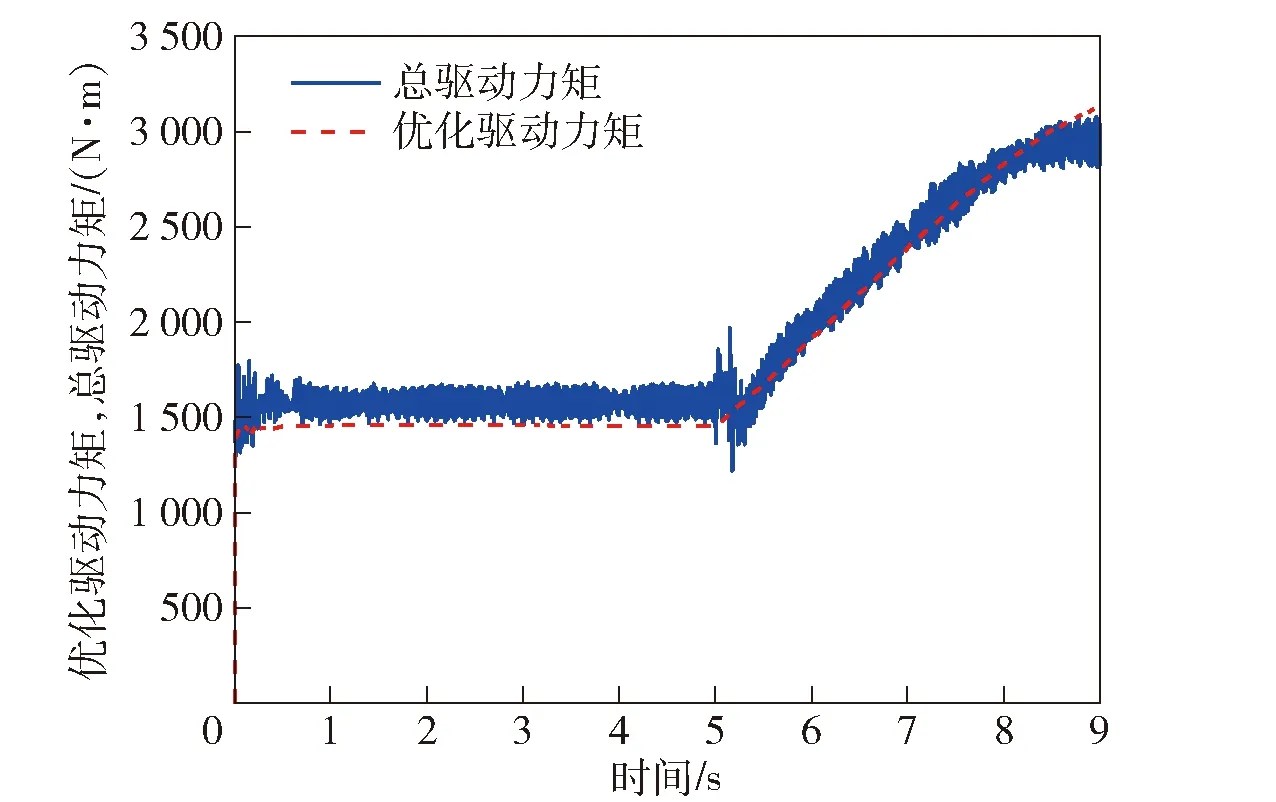
图8 右前摇臂关节的优化驱动力矩和总驱动力矩Fig.8 Optimal and actual torques of right front arm joint
图9所示为整车各车轮地面反作用力的分布情况,在侧倾运动工况下各车轮需要侧向力来平衡运动过程中的侧倾力矩,各车轮的地面切向合力均在摩擦系数μ=0.7的边界约束内。
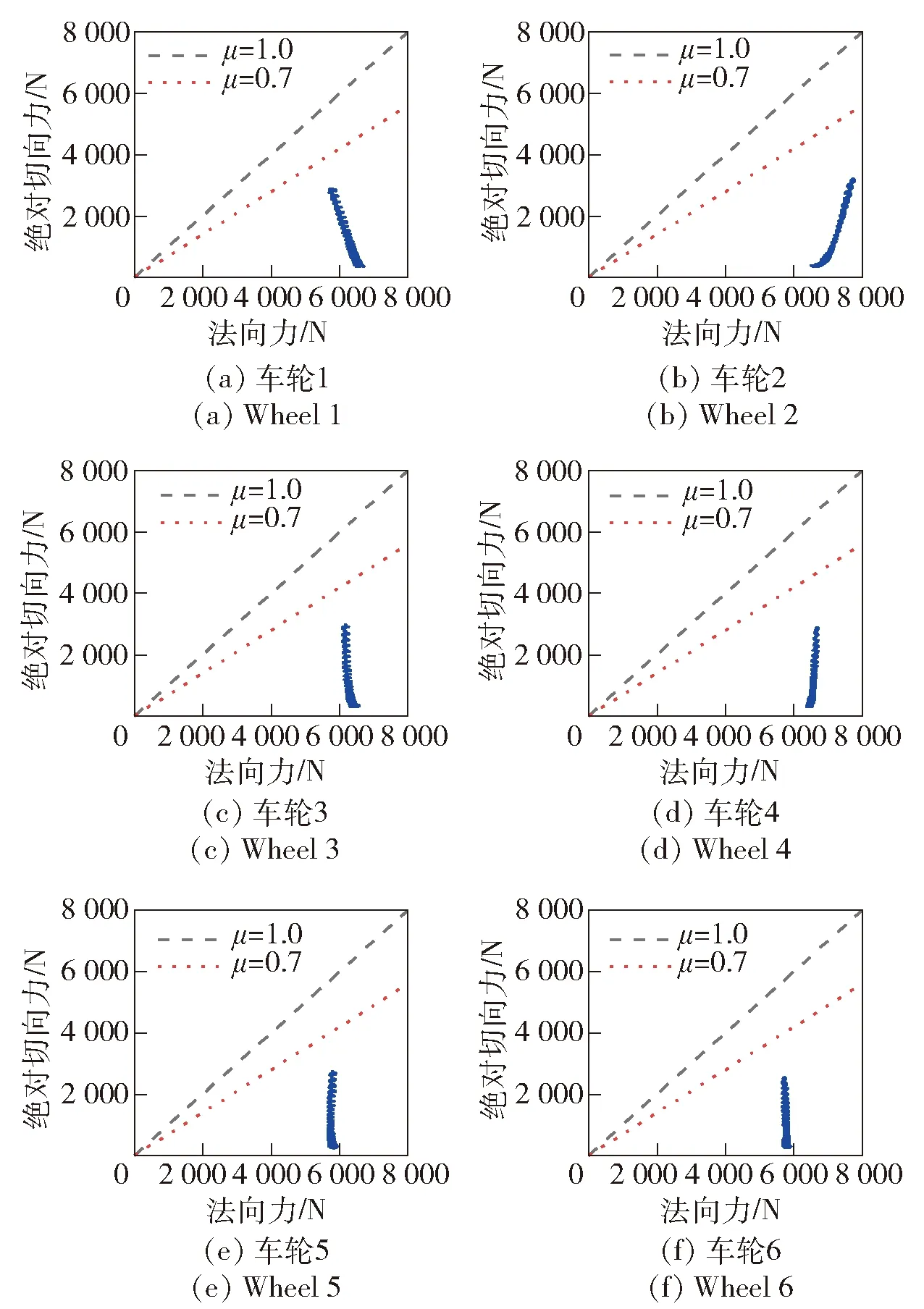
图9 整车各车轮地面反作用力的分布Fig.9 Distribution of ground reaction forces of each wheel
4.2 俯仰姿态
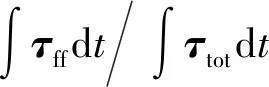
图10 绕y轴俯仰-10°运动Fig.10 -10° pitch motion about y axis
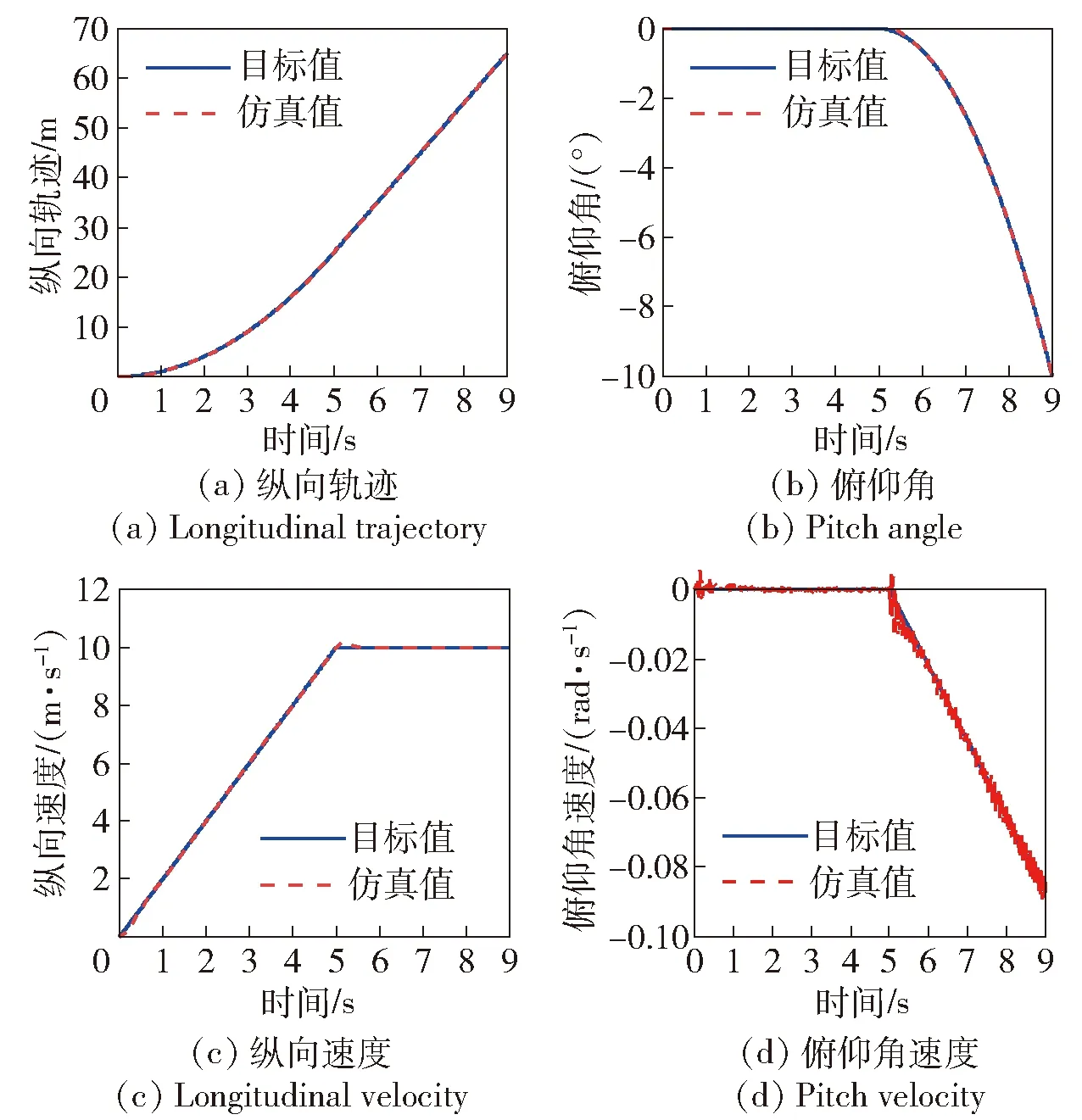
图11 整车质心和姿态运动轨迹的目标值和仿真结果Fig.11 Desired and simulated values of vehicle COM and posture
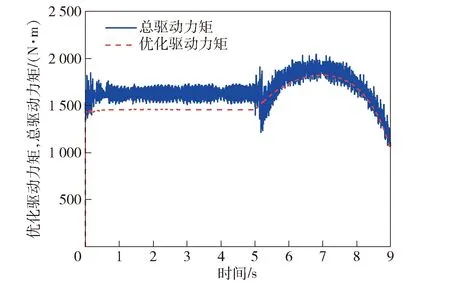
图12 右前摇臂关节的优化驱动力矩和总驱动力矩Fig.12 Optimal and actual torques of right front arm joint
图13所示为俯仰姿态调节过程中,整车各车轮地面反作用力的分布情况,在运动过程中车轮没有侧向力产生,仅通过轴间车轮的纵向力之差产生姿态调节所需求的俯仰力矩。

图13 整车各车轮地面反作用力的分布Fig.13 Distribution of ground reaction forces of each wheel
4.3 侧倾和俯仰联合姿态
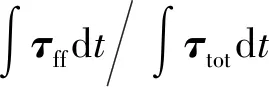
图14 绕x轴5°俯仰和绕y轴-5°俯仰联合运动Fig.14 5° pitch motion about x axis and -5° pitch motion about y axis
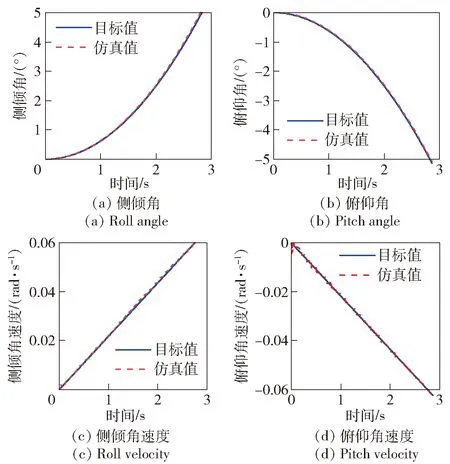
图15 整车姿态运动轨迹的目标值和仿真结果Fig.15 Desired and simulated values of vehicle posture
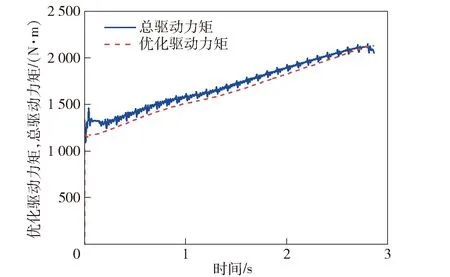
图16 右前摇臂关节的优化驱动力矩和总驱动力矩Fig.16 Optimal and actual torques of right front arm joint
图17所示联合姿态调节过程中,整车各车轮地面反作用力的分布情况,在控制周期内各车轮的地面切向合力被约束在摩擦边界约束内。
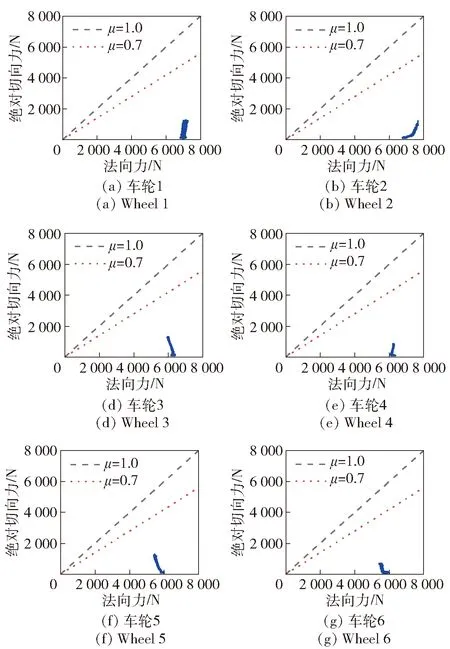
图17 整车各车轮地面反作用力的分布Fig.17 Distribution of ground reaction forces of each wheel
4.4 颠簸路面中的运动姿态保持
为了验证摇臂悬挂机动平台的控制策略对非结构化环境的地形适应能力,如图18所示,本文设计一条颠簸路面,其中平台右侧车轮的行驶路面为平路,左侧车轮的行驶路面为不规则的颠簸路面。仿真要求平台以初始侧倾角10°、俯仰角0°的运动姿态进行速度为0.1 m/s的匀速直线运动,为了保持运动姿态,平台的左侧摇臂需要随颠簸路面摆动以适应路面。

图18 在颠簸路面中保持10°侧倾角行进Fig.18 Moving at 10° roll angle on bumpy road
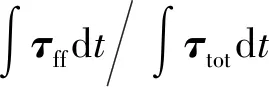
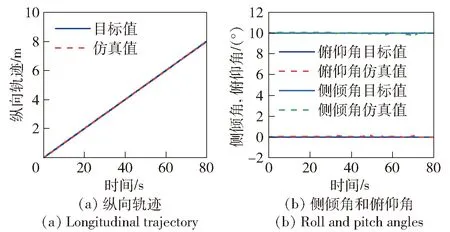
图19 整车姿态运动轨迹的目标值和仿真结果Fig.19 Desired and simulated values of vehicle trajectory
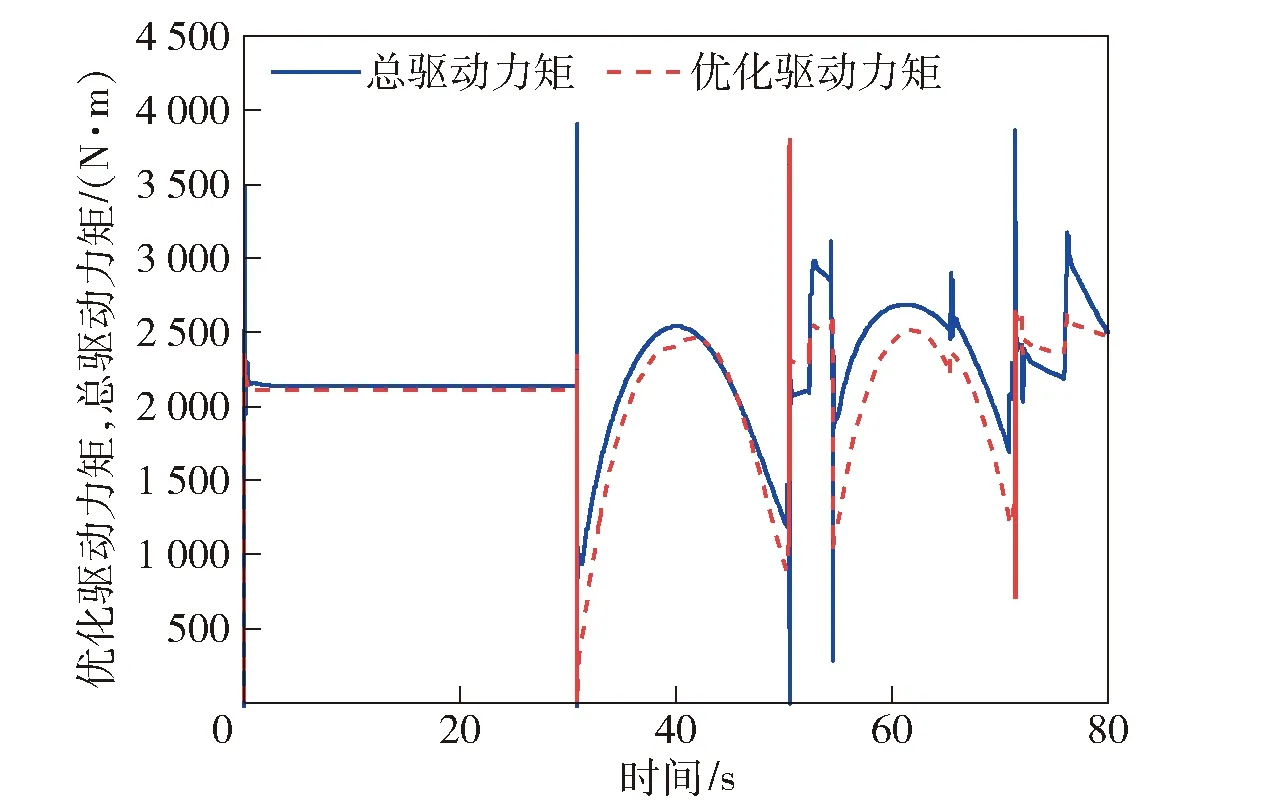
图20 左前摇臂关节的优化驱动力矩和总驱动力矩Fig.20 Optimal and actual torques of left front arm joint
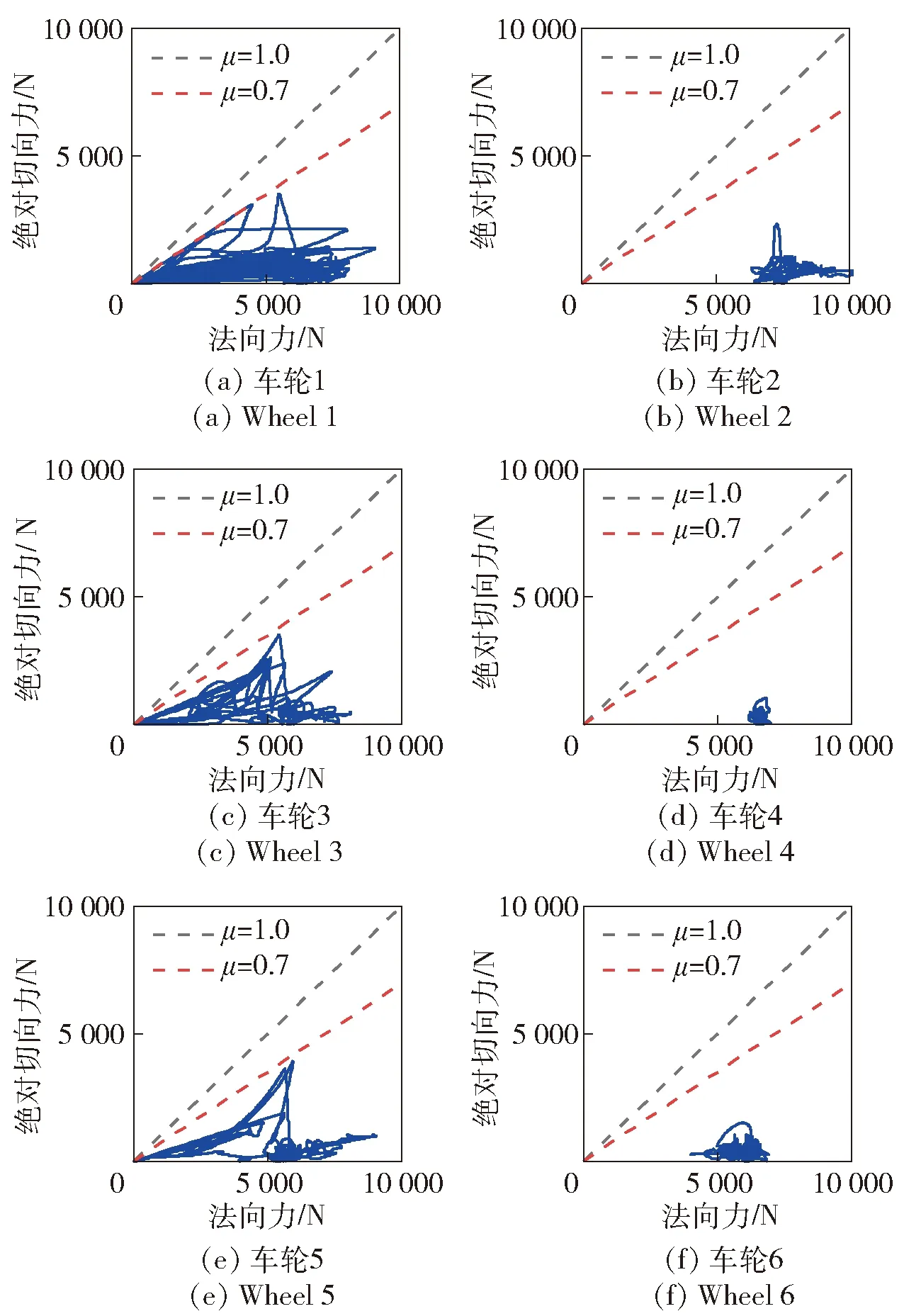
图21 整车各车轮地面反作用力的分布Fig.21 Distribution of ground reaction forces of each wheel
5 结论
本文针对轮腿复合移动车辆自身机构运动自由度多、控制复杂的特性,以摇臂悬挂机动平台为例,提出了一种适用于轮腿复合移动类型车辆进行运动姿态调节的通用优化控制框架,并通过仿真对提出的控制方法进行了验证。得出主要结论如下:
1)在控制器中,考虑整车动力学平衡和车轮地面相互作用约束,用二次规划方法优化了车轮的地面反作用力,进而映射为驱动关节的前馈力矩;通过系统逆运动学方程计算了驱动关节的状态反馈力矩以补偿运动调节过程中的运动偏差,最终实现了对车轮地面反作用力的直接控制。
2)根据系统的动力学方程(6)式,以质心动力学模型和二次规划方法建立的优化控制框架在轮腿机构的运动姿态调节方面具有通用性,本文在摇臂悬挂机动平台上进行了运动姿态调节的仿真验证,仿真结果表明该控制框架可以实现平台在侧倾、俯仰、联合姿态及颠簸路面下的运动姿态调节。
3)控制器的求解时间为0.19 ms,满足实时控制需求;整车运动控制轨迹跟踪相对误差最大为2.74%,驱动关节的前馈驱动力矩在总控制力矩中的占比在92%以上,能够满足整车控制精度的需求。
