“引领、探究、合作、交流”教学模式的实践与分析
2019-12-20江苏省南京市浦口区第三中学邵传经
江苏省南京市浦口区第三中学 邵传经
初中数学课堂要求一线教师能够让不同类型的学生在课堂中展现自己,让他们在课堂中找到自信,提升学好数学的信心和能力。而“引领、探究、合作、交流”这种课堂教学模式经过长期的实践证明完全符合新课标要求,促进了师生共同完成任务,体现了课堂中学生的主体地位,真正让学生感受到数学来源于生活,服务于社会。
一、具体案例设计与分析
1.引领环节
根据这一教学理念,教师是教学环节的引导者,而不是直接干预者。这自然不同于传统教学理念,所以这需要教师转变思维,真正将学习主动权交给学生,让学生发挥主观能动性。正所谓:“授人以鱼不如授人以渔。”教师需要对学生进行引导,而不是直接告诉学生相关知识。
比如,在进行苏教版初中数学八年级上册“三角形全等”这部分的知识点的学习的时候,教师应该通过设置相关问题引领学生。由于该章节涉及三角形全等的条件等学习内容,所以教师不妨根据该部分内容创设相关问题,比如,“全等三角形就是三角形的三条边和三个角相等,所以要想证明三角形全等,只需要让两个三角形的三角和三边相等即可。但是除了这个办法,你还能找出其他简单的方式来证明三角形全等吗?”
2.探究环节
探究环节是引领环节的延伸,教师需要处理好这一环节的教学。在这一环节中,教师应该让学生根据自己提出的问题进行思考,让学生确定所需探究的知识内容,使学生明确学习方向,这样学生在探究的过程中就会倍加注意,从而真正发现所需探究的点所在。
根据教师所提问题,即“还有没有其他的方法来证明三角形全等”,对于还未接触这部分知识的学生而言,这个问题自然有些困难。教师不应该直接让学生看书本上的描述,那样只会让学生停留在学习知识的表面阶段。相比之下,教师应该让学生在自己的草稿纸上画出两个全等三角形,然后对三角形的角和边加以观察。学生在观察的过程中,会试着将其中的角和边去掉,并观察仅凭剩下的条件是否能够证明三角形全等。最后,在教师的引领下,学生就会发现“角角边”“角边角”和“边角边”等证明方法。
3.合作环节
由于学习活动是群体性的活动,教师应该和学生展开合作,并且让学生之间相互合作。提到合作,我们首先会想到“分组讨论”这一教学法。所以,教师不妨将学生进行简单分组,然后让学生相互探讨和合作,集思广益,在合作中解决问题。
学生在探究环节已经确定了数学问题的大致方向,但是学生还需要进一步探讨这些证明方法。教师可以给学生一道数学题:“如下图,已知点B,E,C,F位于同一条直线,其中AB=DE,∠A=∠D且AC∥DF。求证△ABC≌△DEF”。

学生在见到这一题时,需要首先抓住解题的大致方向,也就是运用何种方法进行解题。由于其中涉及平行的知识点,所以学生需要用平行的知识证明角之间的关系,而在条件中已经给出了一条边和一个角的关系,所以学生可以使用“角边角”或者“角角边”的方法,在观察图形之后,那条已知的边长在两个角之间,所以最终确定“角边角”的方法,并最终得出问题的答案。
4.交流环节
交流环节主要是对以上三个环节的弥补。即使再完美的教学过程,都或多或少存在一定的问题,这就需要教师对其进行评价。教师应该让学生发表自己的看法,说说自己在课堂上的收获。教师也应该对学生的表现进行评价,帮助学生在学习过程中扬长避短,规避自己的错误。
比如,在上述解题过程中,学生还不能够熟练使用以上所学的证明方法,教师不应该责骂学生,而应该分析问题的所在。教师应该让学生再回到题目中进行思考,让学生理解这种证明方法的有效性。
二、初中数学课堂四步教学模式的实施效果和分析
“引领、探究、合作、交流”教学模式收到了不错的效果。和传统的教学方式相比,这种教学方法更适应学生的学习,能够帮助学生确定学习的方向,使学生在交流合作中学习。不过该方法也存在部分不足,比如一部分数学基础较弱的学生在课堂上的积极性不高,他们已经习惯了教师的讲解,而不太习惯自己动脑思考,这事实上也是传统应试教育所造成的影响,教师应该在实践环节中把握相关的实施要求,确保学生能够真正学到知识。
在我们区组织的一模数学研讨课上,我上了一节《图形的旋转》,下面是我上课的部分片段。
问题:(回归教材)如右图,在正方形ABCD中,AB=6,AE=3,点E,G分别在边AD,AB上,△ABE经过旋转后得到△BCF。
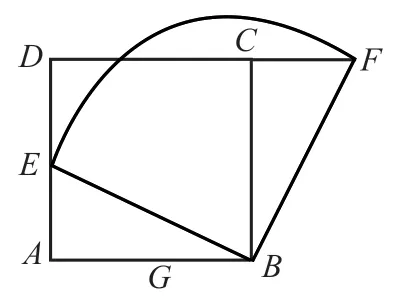
(1)旋转中心是哪一个点?
(2)旋转角为多少度?
(3)在图中画出点G的对应点H。
(4)图中D,C,F三点是否在同一条直线上?
拓展延伸:(1)求点E在远动过程中所经过的路径长。
(2)求线段BE所扫过的面积。
(3)你还能提出哪些能够解决的问题?
同学1:把扇形BEF围成一个圆锥,求圆锥的底面圆的半径。
同学2:设弧EF与DC相交于点M,问点C为FM的中点吗?
同学3:求出扇形BEF与正方形ABCD的重叠面积。
同学4:求出四边形BEMC的面积。
同学5:假设点E为AD上任意一点,四边形BEMC的面积是多少?是否存在最大值或最小值?
同学6:当∠EBM=45°时,求证EM=AE+CM。
……
没想到由书本上的一道题,同学们联想到很多知识板块的内容,起到了非常好的效果,包括圆的性质、函数的最值问题、特殊的四边形的性质等。
课堂中要选择恰当的时候尽可能让学生去思考一些内容,这样更能够激发学生学习的兴趣,也能够加强小组间的交流与合作,这样真正做到了把课堂还给我们的学生,学生是课堂的主人,能够在课堂中有所收获。
