常微分方程初值问题的数值解法中三种算法的比较
2019-12-20南通大学理学院陈俊吉陆海华
南通大学理学院 谢 舒 陈俊吉 陆海华
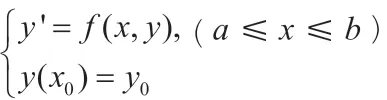
一、数值解法的基本思路和途径
一阶微分方程初值问题的解就是区间上的连续变量的函数,对该问题初值的解,就是求在区间[a,b]上的若干个离散点处的函数的近似值,比如:a≤x1≤x2<x3<…<xn≤b,接着计算出解的近似值:y(x1),y(x2),…,y(xn),一般取x1,x2,…,xn为等距离的点,即x2-x1=x3-x2=…=xn-xn-1=h或者xi=a+ih,i=1,2,3…,n,其中h称为步长。
建立数值方法的第一步,就是把函数离散化。常用的离散化的方法有以下两种:
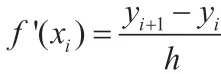
(2)Taylor 展式法。在点x1的附近,y(x)可近似为Taylor 展开式的前P+1 项
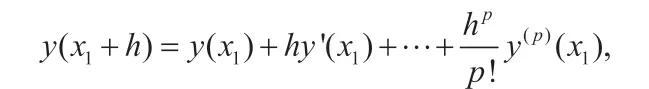
其中P为一正整数。通过微分方程y'=f(x,y),可以逐次把各阶导数y',y'',…,y(P)在x1处的值表示出来。
二、数值方法的导出与分析
1.Euler 方法
Euler 方法是最简单的一种一阶的单步法,缺点是精度较差,优点是公式简单,而且有比较清楚的几何解释,有助于直观理解数值y1是怎样逼近微分方程的精确解的。
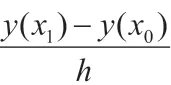
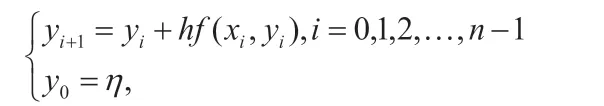
特别地,当P=1 时,近似的Taylor 多项式可化为上述的Euler公式。
2.梯形公式法
梯形公式(TRA)是对Euler 公式的一个改进,梯形表达式为:
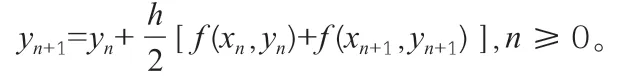
3.Runge-Kutta 方法
相对于其他常微分方程(组)的数值解法,Runge-Kutta 方法阶较高,但它并没有增加微商f(x,y)的次数,所以它相当精确、稳定而且容易编程。
(1)常用的二级二阶Runge-Kutta 公式为:
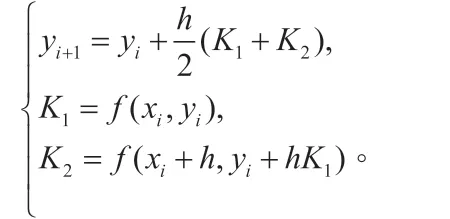
(2)常用的三级三阶Runge-Kutta 公式为
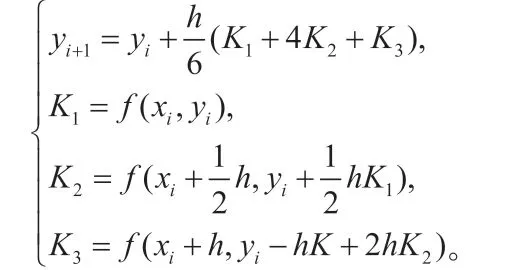
对精度要求不高的实际问题中,我们通常可以采用二级二阶和三级三阶Runge-Kutta 方法。而对于要求较高的问题,我们通常采用如下的四级四阶Runge-Kutta 方法来处理常微分方程的数值解。
(3)常用的四级四阶Runge-Kutta 公式为:
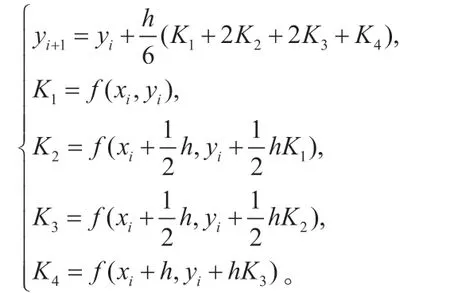
上式在实际的计算过程中是应用最广泛的Runge-Kutta 法公式,也被称为经典的四阶显示Runge-Kutta 公式。
三、三种方法的实例比较
我们通过两个具体的实例分析解析解和三种算法得到的数值解之间的关系。
1.一阶常微分方程实例(1)
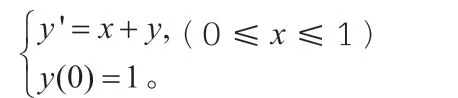
(1)解析解
利用y'+p(x)y=Q(x)的通解公式
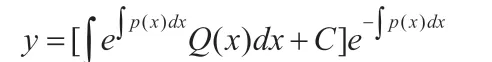
可直接得到本例的通解y=Cex-x-1。将初值条件y(0)=1 代入可得本例的解为y=2ex-x-1。
(2)利用三种算法求其数值解。分别选取步长为h=0.1,利用三种算法来求解该方程在x=0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0处的数值解,将数值解的结果与解析式所求解的结果作比较。首先分别利用Euler 公式、梯形公式公式、四级四阶Runge-Kutta 公式,使用Matlab 求解方程的数值解。
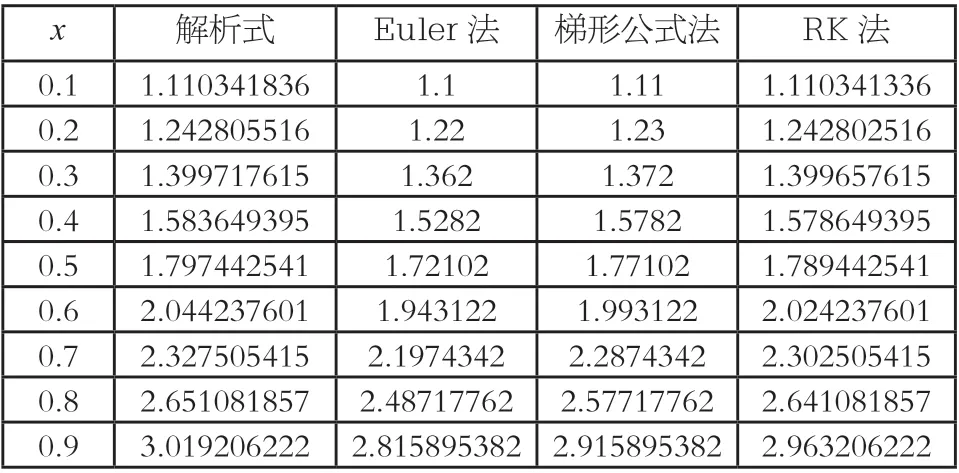
表1 三种解法的数值解和解析解
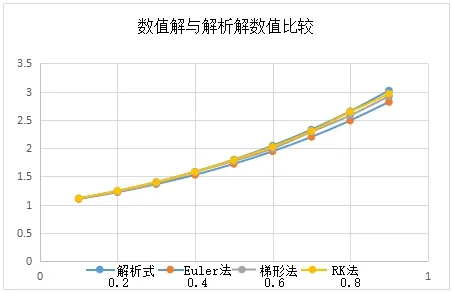
图2 数值解与解析解数值比较
从图1 和图2 中可以很清晰地看出四级四阶Runge-Kutta 方法比梯形公式法和Euler 公式法与解析解更加接近。近似度最差的是Euler 法,Euler 法的数值解与解析解的数值差最大,梯形公式法优于Euler 法,效果最好的还是Runge-Kutta 法。Runge-Kutta 法得到的数值解明显接近解析解的值,且随着数值增加,梯形公式法和Euler 法与解析解的误差越来越大,但是Runge-Kutta 法的计算过于复杂,而Euler 相对而言简单许多。同时,我们对相关数值解和解析解进行误差分析,如图3。
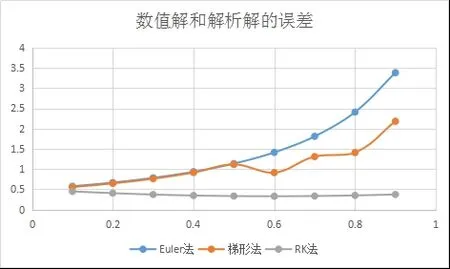
图3 数值解和解析解的误差
综上,Runge-Kutta 法的数值解明显精确度更高,更加接近于解析解,误差也接近于0,但是其计算复杂程度明显较高,计算机编程代码比Euler 法和梯形公式法复杂许多,所以在实际应用时要灵活采取不同的方法计算。
2.三种方法的实例比较(2)
我们考虑如下常微分方程初值问题的解析解与数值解

选取步长为h=0.1,再利用解析法和数值解法求解该方程在x=0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0 处的数值解,根据所求结果,比较数值解的结果与解析式解的结果及两种方法的截断误差和误差绝对值。
(1)解析解
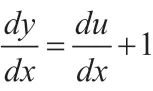
(2)利用三种算法求其数值解。分别选取步长为h=0.1,再利用解析法和数值解法求解该方程在x=0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0 处的数值解,根据所求结果,比较数值解的结果与解析式解的结果及两种方法的截断误差和误差绝对值。同例1,我们可以得到该常微分方程数值解和解析解数值的比较图以及误差分析图(如图4,图5)。
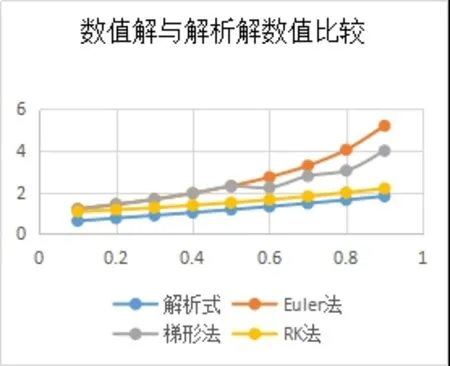
图4 数值解与解析解数值比较
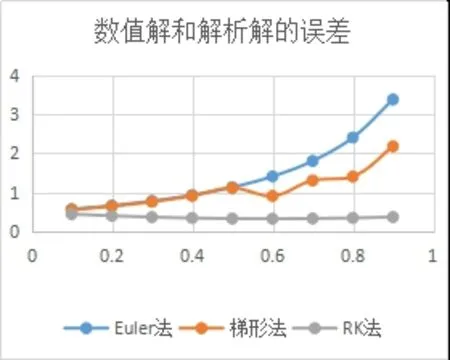
图5 数值解和解析解的误差
从图4 和图5 中我们可以看出,当x的取值接近初值时,三个数值解与解析解非常接近,当随着x的逐渐增大,Euler 法的数值越来越偏离解析值,梯形法次之,Runge-Kutta法的数值与解析值最接近,并且误差也几乎为0。这一结果和例1 得到的结果是统一的。
