小学数学教学中数学建模的应用

江西省抚州市东临新区太阳中心小学 黎淑华

数学从本质上来说就是一门枯燥的学科，它涵盖着概念、抽象、性质、几何、函数等，学生在学习的过程中会比较困难，而且容易产生厌学的心理。教师在教学时就需要针对学生的具体问题采用能提高教学效率的教学方式。如果采用数学建模的教学方式，将可以在很大程度上将数学的抽象知识转化为实际的数学模型，能够更加直观地在学生的大脑中呈现，让学生可以更加容易地理解抽象的数学知识，有助于提高学生学习数学的兴趣，更大程度上激发他们的学习潜能。

一、数学建模的概念及重要意义

“数学建模”从字面上的意思来说，其实就是通过所学的数学知识来建立一个看得到的、能够观察出来的数学模型，这种数学模型能够很好地帮助学生去理解抽象的数学知识。其实数学模型就像一台转换器，能够将抽象的数学影像转换成具体的数学物象。广义上来说，数学知识中的一些公式、几何关系、函数图像等都是从现实世界中的原型抽象得到的，所以学生就可以通过其在现实世界的原型来寻找与数学的关系，得到解题思路。 数学模型的建立反映了特定问题和一些具体事物之间的数学关系，表达的是数学中各个变量中的联系。教师要通过数学建模的方式，积极培养学生的时空观、数字感、应用意识和推理能力。

建立了一个完整的数学模型后，教师的教学效率会得到提高。传统的小学数学教学方法总是单一的，导致教师传递给学生的数学知识信息永远是抽象的，学生对数学知识的印象不深刻。而运用数学建模会将抽象的数学问题具体化，使学生能更好地理解数学知识，对平时容易遗忘的知识点加深印象，此外，还能提高学生对数学的学习兴趣，打破学生对数学传统枯燥的认知，让学生在学习数学时能有清晰的学习脉络，解题时思路清晰。

二、数学建模的具体应用策略

1.数学建模的前期准备

教师必须做好数学建模的前期指导工作，引导学生建立一个良好优秀的数学模型。首先，教师要引导学生不断去发现事物内部或外部的共性联系，让学生主动去思考如何把已学的知识和相似的新知识进行结合。将旧知识与新知识进行结合，不仅能够帮助学生建立数学模型，还能降低学生在学习过程中的建模难度。

比如，教师在讲到“图形面积”时，在已经介绍了三角形的面积如何计算之后，教师可以引导学生去发现四边形的面积可以分割成什么，而这两个图形与四边形的面积算法又有什么联系。在思考过程中，学生便可以很快发现，四边形可以分成两个三角形，而这两个三角形的面积之和便是四边形的面积，学生还会发现三角形和四边形的面积公式之间存在着二倍的联系。这样直观地让学生感受到图形的变换、公式之间的联系、事物内部之间的共性与联系，都会加深学生对知识点的印象，提高学生的学习效率、活动思维能力，激发学生的学习潜能，使学生能主动去发现问题并解决问题。

2.合作交流，主动构建数学模型

数学家华罗庚通过多年总结的经验告诉后人，学习数学不仅仅要记住其中的结论、定律、公式等，还应该多多思考这些数学原理是怎么来的。只有经过主动探索，主动学习发现，主动动手实践，学生才能在学习过程中达到质变的过程。因此，教师要善于引导学生进行探讨性活动。

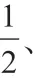
3.应用问题中进行数学建模

小学数学问题中的应用题十分考查学生的数学建模能力。比如，遇到问题：小明从家到学校需要骑车8 分钟，每分钟骑车210 米，问小明家离学校多远？这是一个十分简单的速度乘以时间的问题，当把题目中的8 分钟换成“从6：56～7：04”时，学生需要敏锐地意识到时间的转换，万变不离其宗。运用数学建模能使学生更快速地找到解题的突破口，从而对数学产生极大兴趣。

综上所述，在小学数学教学过程中运用数学思维建模的方式，能使学生体验到数学的魅力所在，同时提高教学效率，使课堂有效性得到大大的提高。