一元二次不等式解法的“逆向应用”

王继山

(辽宁省葫芦岛市第一高级中学 125100)

一元二次不等式解法的“逆向应用”，可以借助二次函数的图象，对二次不等式中的参数进行求解，或是比较大小，同时也可以通过对一元二次不等式进行等价变形，巧妙地解决问题.解一元二次不等式作为解决问题的基本运算，在新课改的高考的考查中通常蕴含在题目的计算过程中，而含有参数的问题又是高考中常考的知识点．

一、借助二次函数的图象，巧解含参二次不等式问题

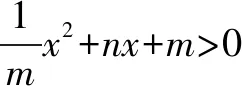
(2)如果关于x的不等式ax2+bx+c<0的解集为{x|xn}(m0的解集.

分析借助对应二次函数的图象及给定不等式的解集，我们可得到对应二次方程的两个实数根和二次项系数与零的大小关系，这就是此类问题的求解思路.

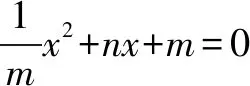
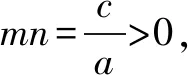
评注(1)若给定一元二次不等式的解集为{x|a≤x≤b}或{x|x≤a或x≥b}或{x|ab}的形式，则对应一元二次方程的两个实数根分别是a和b.

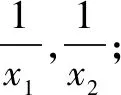
二、借助等价变形，巧解含参分式不等式问题

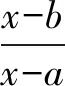
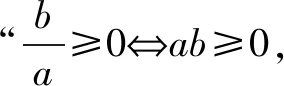
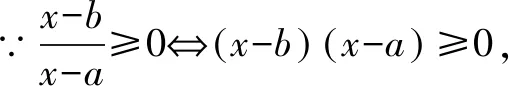
故所求不等式的解集为{x|-2≤x<1}.

评注(1)由分母x-a≠0 及题设可求得a=2，这是本题整个分析、求解的切入点.(2)一般地，求解分式不等式时要特别关注转化的等价性；否则，极易出错.

三、借助二次函数的图象，巧解比较大小问题

例3 已知函数f(x)=(x-a)(x-b)+1，且a

分析本题可以借助二次函数f(x)的图象来分析，通过探究实数a,b,m,n对应的几何意义，以便从“形”的角度顺利获解.

解析如图，先作直线y=1的图象，再作f(x)的图象，二者交于A、B两点.

∵方程f(x)=0的两根分别为m和n，且m

∴根据题设条件就可以确定m和n在图象上的实际位置，即f(x)与x轴的交点，且m

∵方程f(x)=1，即(x-a)(x-b)=0的两根分别为

a和b，且a

故由图观察即知，所求实数a,b,m,n的大小关系是a

评注一般地，运用图象法分析、解决问题时，必须明确方程f(x)=c的根就是函数f(x)的图象与直线y=c的交点的横坐标；特别地，方程f(x)=0的根就是函数f(x)的图象与x轴交点的横坐标.

综上，运用一元二次不等式的解题方法对函数定义域、值域以及以后处理的其它类型不等式,都起着十分重要的作用.逆向应用一元二次不等式的解法的关键在于：要善于联系对应二次方程的根或对应二次函数的图象进行灵活地思考、分析.