由毕达哥拉斯定理证明想到的

李渊科 指导教师：班春虹

(天津经济技术开发区第一中学 300000)

毕达哥拉斯定理一般指勾股定理，是一个基本的几何定理.虽然我们在初中就对它有一定的了解，但很多同学对它的认知只限于a2+b2=c2，但毕达哥拉斯定理所涉及的远远不止这些.在中国，周朝时期的商高提出了“勾三股四弦五”的勾股定理的特例；在西方，最早提出并证明此定理的为公元前6世纪古希腊的毕达哥拉斯学派，对于这个发展悠久的定理，作为中学生的我们有许多的知识要从中汲取.

一、毕达哥拉斯定理的内容

在平面内的一个直角三角形中，两个直角边边长的平方加起来等于斜边长的平方.如果设直角三角形的两条直角边长度分别是a和b，斜边长度是c，那么可以用数学语言表达：

a2+b2=c2.

二、毕达哥拉斯定理的证明

毕达哥拉斯定理现约有500种证明方法，是数学定理中证明方法最多的定理之一.下面介绍其中2种方法：

1.赵爽弦图

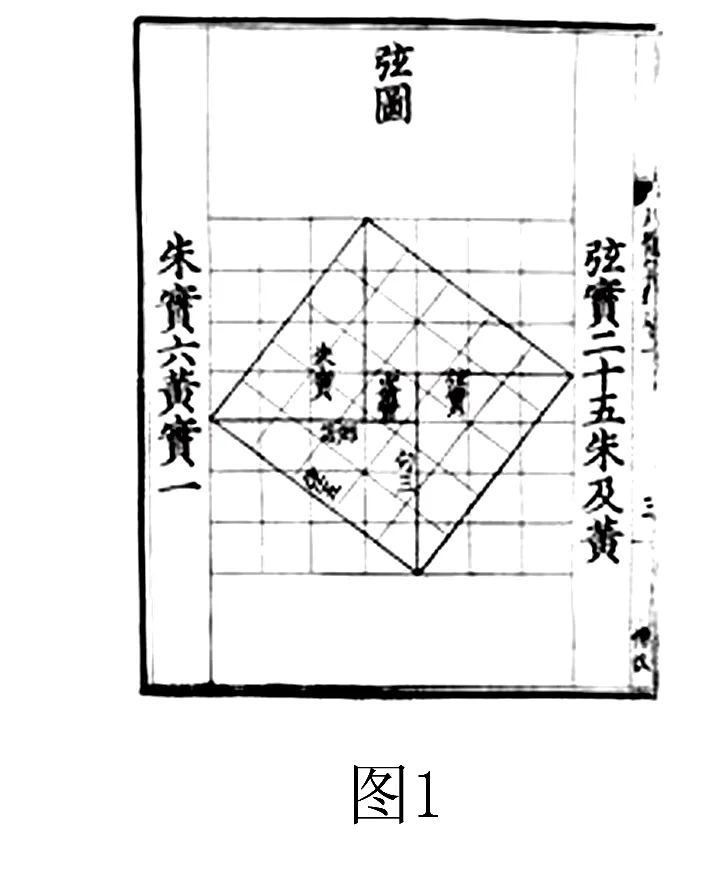
《九章算术》中，赵爽描述此图：“勾股各自乘，并之为玄实.开方除之，即玄.案玄图有可以勾股相乘为朱实二，倍之为朱实四…其倍玄为广袤合.令勾股见者自乘为其实.四实以减之，开其余，所得为差.以差减合半其余为广.减广于玄即所求也.”

2.欧几里得证法

在欧几里得的《几何原本》一书中给出勾股定理的以下证明.

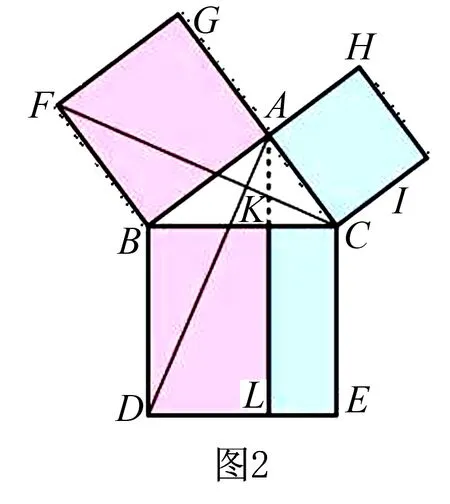
设△ABC为一直角三角形，其中A为直角.从A点划一直线至对边，使其垂直于对边.延长此线把对边上的正方形一分为二，其面积分别与其余两个正方形相等.

在这个定理的证明中，我们需要如下四个辅助定理：

如果两个三角形有两组对应边和这两组边所夹的角相等，则两三角形全等.(SAS)

三角形面积是任一同底同高之平行四边形面积的一半.

任意一个正方形的面积等于其二边长的乘积.

任意一个矩形的面积等于其二邻边长的乘积.

证明的思路为：从A点划一直线至对边，使其垂直于对边.延长此线把对边上的正方形一分为二，把上方的两个正方形，通过等高同底的三角形，以其面积关系，转换成下方两个同等面积的长方形.

三、数形结合思想

在以上毕达哥拉斯定理的证明中，都用到同一个思想：数形结合思想.作为一种数学思想方法，数形结合的应用大致又可分为两种情形：或者借助于数的精确性来阐明形的某些属性，或者借助形的几何直观性来阐明数之间某种关系，即数形结合包括两个方面：第一种情形是“以数解形”，而第二种情形是“以形助数”.对于刚上高一的我来说，数形结合思想在新知识中有许多应用.

1.集合问题

(1)与数轴结合

例1己知A={x|a≤x≤a+3},B={x|x2-4x-5>0}.

(1)若A∩B=∅,求a的取值范围;

(2)若A∪B=B,求a的取值范围.

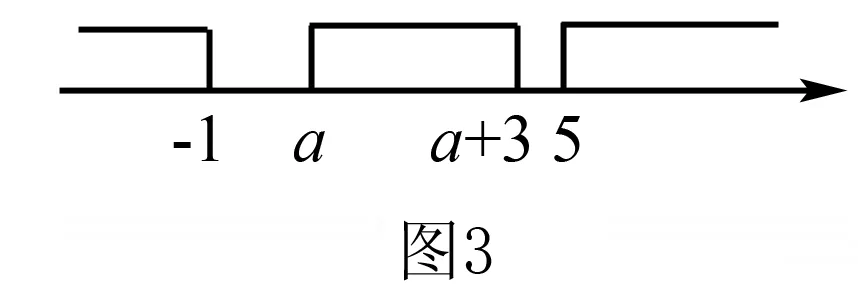
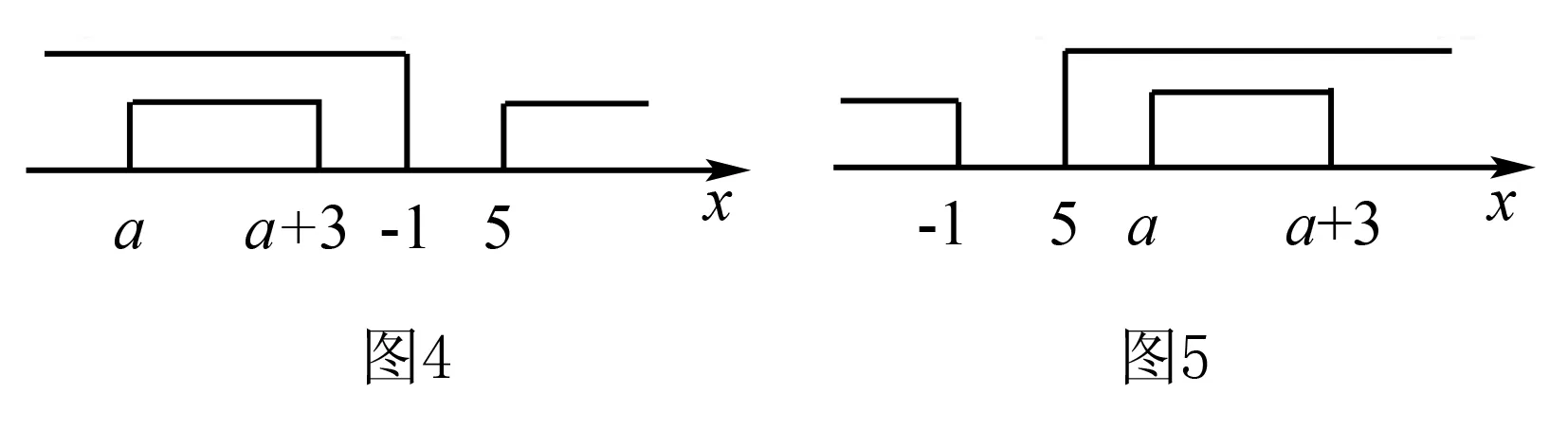
分析在数轴上标出集合A、B所含元素的范围,利用A、B的位置关系确定参数a的取值范围.

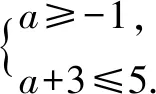
(2)由A∪B=B知A⊆B,利用数轴得到满足A∪B=B的不等式a+3<-1,或a>5,所以实数a的取值范围是{a|a<-4，或a>5}.

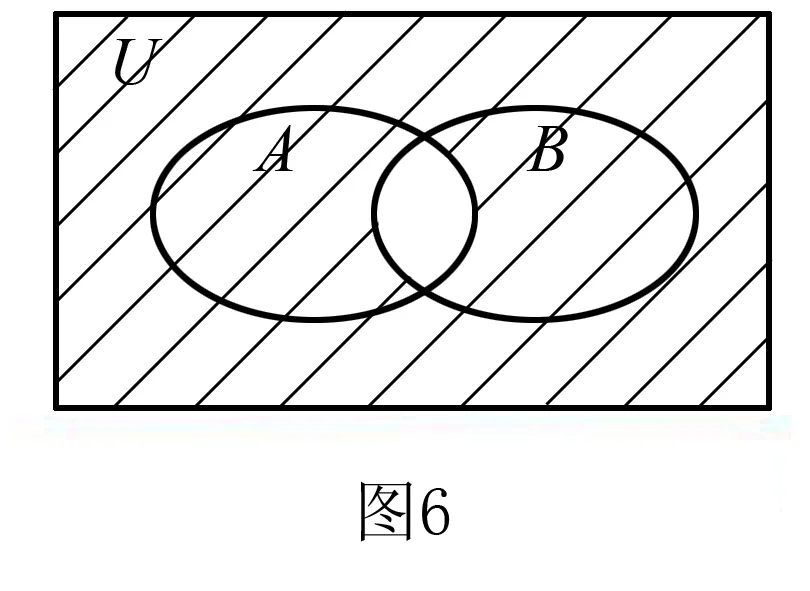
(2)与Venn图结合例：

这个Venn图表示全集U，阴影部分表示A与B的交集关于U的补集.

2.方程与不等式

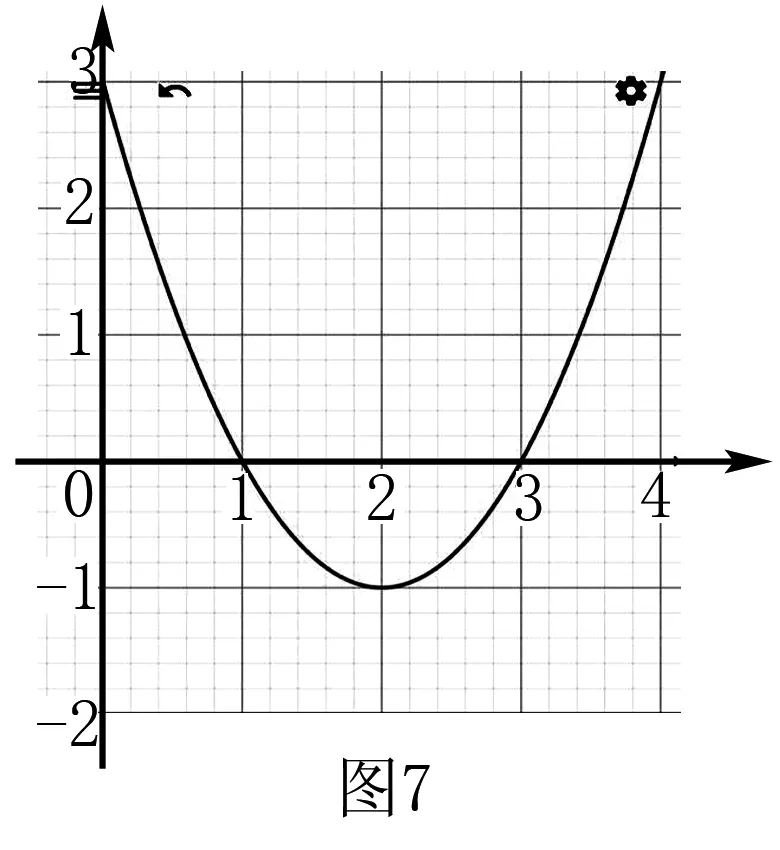
例2x2-4x+3=0为一个一元二次方程，相应函数y=x2-4x+3的图象与x轴的交点坐标为方程x2-4x+3=0的根.

x2-4x+3>0为一个一元二次不等式，从函数图象上可看出，不等式的解集为{x|x<1或x>3}.

x2-4x+3<0为一个一元二次不等式，从函数图象上可看出，不等式的解集为{x|1

毕达哥拉斯定理的证明是论证几何的发端；是历史上第一个把数与形联系起来的定理．这条定理在几何学中是一颗光彩夺目的明珠，被誉为“几何学的基石”.本文对毕达哥拉斯定理以及其中用到的数形结合思想在高一数学中的应用进行了浅要的研究，由于专业性较强，一些工作并未做到完美，研究比较粗糙，这是作者今后努力的方向.