基于B型灰色关联度的雷达与ESM航迹关联算法

顾一休，李 军，邱令存，曹 政

(1. 南京理工大学自动化学院，江苏 南京，210094； 2. 上海机电工程研究所，上海 201109)

0 引 言

异类传感器的数据融合向来是多传感器数据融合[1-3]的重点，而雷达与电子侦察设备(electronic support measure,ESM)的融合更是其中的典型[4]。雷达作为主动传感器，能够提供目标完整位置信息，但由于要辐射一定的能量，因而易于受到欺骗和摧毁。ESM作为被动传感器，不辐射能量，隐蔽性较好，且能获得目标较高的属性信息，完成对目标的识别，但是不能测量目标距离。雷达与ESM进行融合后得到的信息有助于实现更好的目标跟踪与目标识别，提高系统的可靠性和生存能力。为了完成雷达与ESM的数据融合[5]，首先需要实现的是它们的航迹关联。因而，雷达与ESM航迹关联的重要性不言而喻。

1 灰色航迹关联

1.1 B型灰色关联度

B型灰色关联度[6]综合考虑总体位移差、总体一阶斜率差与总体二阶斜率差，来全面描述事物之间发展过程的异同性和关联程度。

关于B型关联度的定义如下：

设参考序列为X0=(x0(1),x0(2),…,x0(n))；

比较序列为Xi=(xi(1),xi(2),…,xi(n)),i=1,2,…,m。

令

(1)

(2)

-2(xi(k)-x0(k))+xi(k-1)-x0(k-1)|

(3)

则B型关联度的计算公式为

(4)

由式(1)～(3)显见

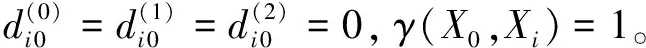
由式(4)可知

γ(X0,Xi)∈(0,1]

1.2 灰色关联矩阵

设Yi(i=1,2,…,s)为系统特征行为序列，Xj(j=1,2,…,m)为相关因素行为序列，且Yi、Xj长度相同；γij为Yi与Xj的灰色关联度，则称以下矩阵为灰色关联矩阵。

(5)

在上列矩阵的基础上，给定λ∈(0,1)，则式(6)中的Γλ被称为灰色关联矩阵Γ的λ-截灰色关联矩阵，为

(6)

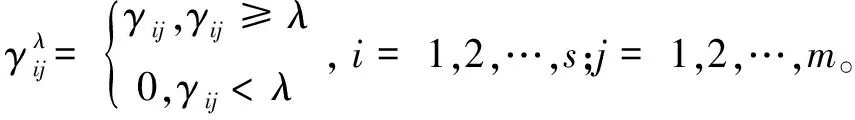
2 雷达与ESM航迹关联

2.1 问题描述

在雷达与ESM的航迹关联问题中，ESM一般只提供目标的方位数据，雷达提供的有距离、角度、速度等位置信息，所以雷达和ESM关联可利用的公共信息只有雷达与ESM的方位角数据[8]。不失一般性地在此假设：

1) 雷达在探测区域内探测到S个目标，目标的量测序列为Z(k)={Zi(k)|i=1,2,…,S;k=1,2,…,N1}，其中，Zi(k)=[ri(k),αi(k)]T，ri(k)，αi(k)分别为雷达探测到的第i条航迹在k时刻的距离和方位角，N1为探测次数。

2) ESM在探测区域内探测到M个目标，目标的方位角序列X(k)={Xj(k)|j=1,2,…,M;k=1,2,…,N2}，其中，Xj(k)=βj(k)，βj(k)为ESM的第j条航迹在k时刻的方位角，N2为探测次数。

3) 假定雷达与ESM测得的不同航迹均属于不同目标，即同一传感器的不同航迹互不关联。

2.2 时空对准

2.2.1ESM数据处理

ESM方位角测量误差较大，有必要降低误差较大的ESM测量数据带来的影响，本文采用基于灰色代数曲线模型(grey algebraical curve model，GAM)[9-10]的方法对ESM数据进行处理。

将ESM的原始测量数据βj(k)记为R(0)(t)(t=1,2,3,…,N2)，具体的平滑处理过程如下。

1) 对原始测量序列进行累加，生成R(1)(t)，令

(7)

2) 求解GAM的系数向量A

构造GAM

(8)

记

A=[a0,a1,a2,…,an]T

Y=[R(1)(1),R(1)(2),R(1)(3),…,R(1)(N2)]T

运用最小二乘法，可以得到系数向量A为

A=[BTB]-1BTY

(9)

综合考虑模型精度(由模型阶数n决定)与计算量(由样本数N2决定)，本文将n选取为n=4。

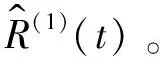
(10)

2.2.2雷达数据处理

在进行雷达与ESM的航迹关联之前，考虑到雷达测量周期大于ESM测量周期，造成单个融合周期内雷达测得的航迹数小于ESM测得的目标数，同时雷达和ESM的量测坐标系不同，为了顺利进行航迹关联，有必要对雷达与ESM数据进行时空统一[11]。由于雷达兼具距离与方位角二维信息，而ESM与雷达的公用信息仅为一维方位角信息，因而融合中心的选取只能以ESM为中心。将雷达测量数据(方位、距离)转换成以ESM为中心的角度数据，再用内插外推的方法将转换后的雷达数据统一到平滑后的ESM测量序列中，具体公式为

(11)

式中，ti、ti+1分别为雷达的相邻测量时间，且ti≤t≤ti+1。

2.3 关联算法

雷达与ESM量测数据经过上述方法处理后，已经形成了具有相同时标的方位角数据。设ESM平滑后的方位角信息为

(12)

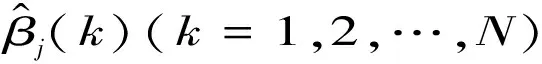
雷达数据转换到以ESM为中心后的角度数据为

(13)

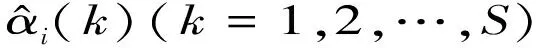
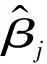
本文提出的航迹关联算法具体过程如下：

1) 将同地配置的雷达与ESM测量数据按照上述方法进行预处理，形成如式(12)～(13)表示的具有相同时标的方位角序列；

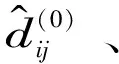
(14)

(15)

(16)

则雷达的第i条航迹与ESM的第j条航迹之间的B型灰色关联度为

(17)

其中：i=1,2,…S;j=1,2…M。

3) 建立航迹灰色关联矩阵

(18)

rij为由式(17)算出的雷达的第i条航迹与ESM的第j条航迹的B型灰色关联度。

4) 计算λ-截航迹灰色关联矩阵

航迹灰色关联矩阵Γ中的元素γij值的大小与不同航迹对之间关联程度的高低成正比，其值越小，则关联可能性越低。所以，可以设置一个阈值λ，剔除灰色关联度低于λ的航迹对。根据式(6)可知λ<1，本文设λ=0.5。根据式(19)～(20)来计算λ-截航迹灰色关联矩阵Γλ，即

(19)

(20)

5) 判定规则

在上一步计算出的Γλ基础上进行关联判定，具体判定规则如下：

① 在Γλ中寻找值最大的元素，即B型灰色关联度最大的航迹对，也可以认为是最有可能相关的航迹对。假设所找的元素在Γλ矩阵的第m行n列，则做出判定：雷达的第m条航迹与ESM的第n条航迹关联。

② 在问题描述阶段已经做出了来自同一传感器的航迹是互不相关的假设，那么雷达的不同航迹不会同时关联到ESM的同一航迹，在规则①中已做出了判定，则雷达的第m条航迹已不会与ESM的其他航迹关联。同理，ESM的第n条航迹也是相同情况。因此可将Γλ矩阵的m行n列所有元素的值置0。

③ 当Γλ中元素全为零时，结束判定，否则转①。

3 仿真实验

3.1 仿真环境描述

假设有同地配置的雷达和ESM位于坐标原点，ESM测量周期为1 s，雷达探测周期为2 s，且航迹数据是在相同的坐标系下测量的，仿真持续时间为600 s，对探测区域内的4个飞行目标进行量测。ESM探测到目标1、目标2、目标3，雷达探测到目标1、目标2、目标3、目标4。融合中心接收雷达与ESM的量测数据并对它们进行航迹关联判定。按照2.2节中所提的方法对雷达与ESM数据进行处理，使之形成具有相同时标的方位序列。

飞行仿真目标的具体运动模型如下：4个飞行目标均做匀速直线运动；目标1初始位置为[5 000 m，4 000 m，3 000 m]，速度为[5 m/s，2 m/s，1 m/s]；目标2初始位置为[5 100 m，4 100 m，3 100 m]，速度为[5 m/s,2 m/s,1 m/s]；目标3初始位置为[5 500 m，4 500 m，3 500 m]，速度为[6 m/s，2.5 m/s，1.5 m/s]；飞行目标4初始位置为[5 600 m，4 600 m，3 600 m]，速度为[6 m/s,2.5 m/s,1.5 m/s]。目标1、2、3、4的飞行轨迹相对密集。

目标真实方位角如图1所示，雷达测量到的4个目标相对于原点的方位角数据如图2所示。

图1 目标方位角Fig.1 Target azimuth angle

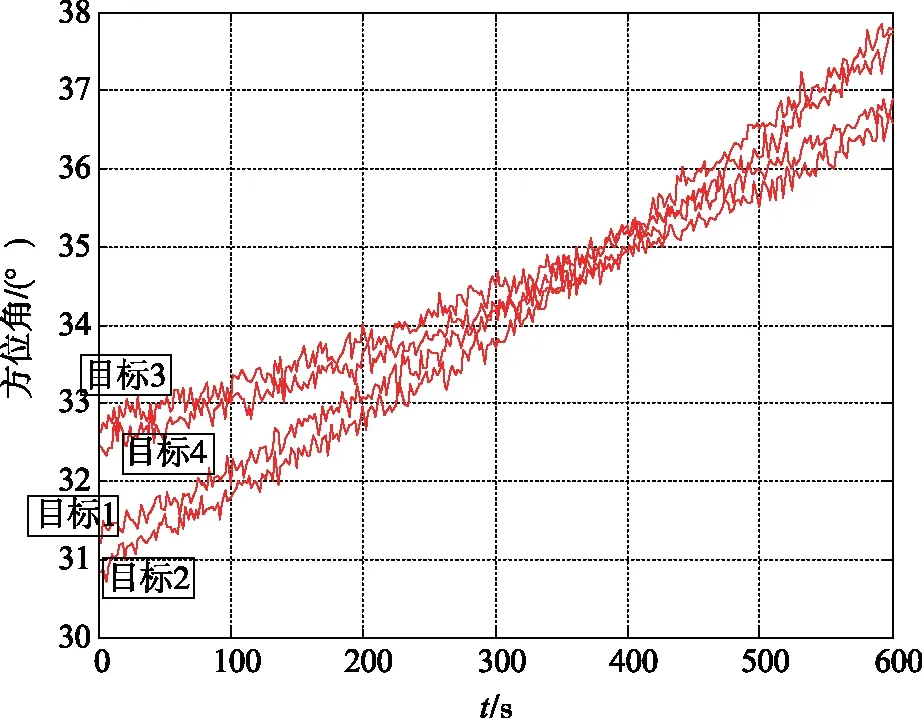
图2 雷达测得方位角Fig.2 Azimuth angle measured by radar

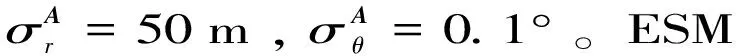
3.2 仿真实验结果

为了直观地看出关联效果，本文用正确关联概率来表示。正确关联概率的计算方法为：判出雷达目标1、2、3分别与ESM目标1、2、3关联的次数与总仿真次数之比。在Matlab上对序列数N0=9、N0=12、N0=15的情况分别进行250次仿真，仿真结果如表1所示。

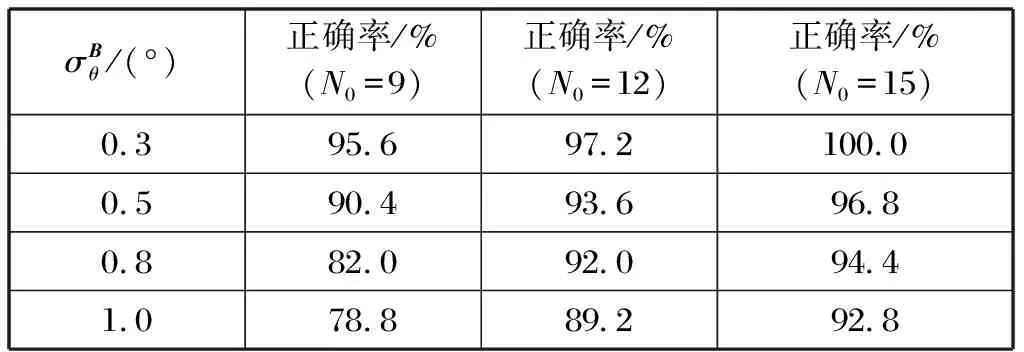
表1 关联效果Tab.1 Associated effect

从仿真结果可知：1)在运动轨迹密集的情况下，本文算法保持着较高的正确率；2)正确关联概率随着序列数N0的增加而增加；3)ESM的量测精度越高，正确关联概率越高。

4 结束语

雷达与ESM的航迹关联属于典型的异类传感器相关问题，由于雷达与ESM各自的特点，它们唯一共有的信息就是目标的方位角，加上ESM测量精度不高，因此关联难度较大。本文先用GAM模型对ESM测量数据进行平滑，减小其中误差较大的数据对关联结果的影响；再将雷达数据统一到ESM数据中，完成时空对准，形成两组具有相同时标的方位角序列；最后计算出这两组数据的B型灰色关联度，根据判定规则来选出关联航迹对。从仿真结果来看，该方法对样本容量没有特殊要求，也不需要典型分布规律，计算简单，易于工程实现。