基于多目标优化的防空武器拦截方案设计方法
2019-12-18赖文星丁士洲
赖文星,贾 军,鲍 然,丁士洲
(上海机电工程研究所,上海 201109)
0 引 言
现代化空袭作战由包括巡航导弹、弹道导弹、制导炸弹、轰炸机、攻击机、直升机在内的多种武器相互配合完成,传统防空武器拦截方案设计方法难以适应全天候、全空域、多层次、饱和式的空袭模式。目前,防空武器拦截方案设计方法尚未形成一套完善的理论体系,大部分研究仅针对特定实际问题,依据一定的假设准则建立优化数学模型,难以同时实现防空效能与拦截成本的最优化。
文献[1]将要地防空区域网格化,建立以防御贡献程度为目标的单目标优化模型,并采用Memetic算法进行求解,最终实现网络化火控系统下对防空武器单元的优化。文献[2]基于排队论的敌方空袭目标突防概率计算方法,建立以防空覆盖程度、武器密集程度、防线划分为优化目标的多目标优化模型,最终获得满足部署地形条件、防空网络完整覆盖的扇形要地防空拦截方案,但扇形要地防空适应范围受限。文献[3]以防空部署均匀程度、防空拦截纵深、防空部署前伸、防空掩护部署、防空武器接力制导为优化目标,建立多层次拦截防线、靠前均匀部署、纵深掩护制导的高维要地防空武器拦截的数学模型,但仅仅考虑防空能力并未考虑部署成本。在考虑防空武器性能参数、部署地形条件约束、敌方来袭目标的进攻方式等条件下,当前已有的数学模型可靠度不高、算法优化结果不理想,还有待进一步深入研究。
针对由多种类型(远程、中程、近程等)防空武器混编构成的火力拦截体系,本文通过建立防空武器多目标拦截方案的数学模型,采用NSGA-II多目标进化算法进行求解,最终获得同时满足空袭目标突防概率最小化和拦截成本最小化的防空武器拦截方案。
1 防空武器拦截方案多目标优化模型
1.1 攻防双方基本假设
防御方在保卫目标周围混合部署着m种不同类型的防空武器M1,M2,…,Mm,每种类型的防空武器数量分别为X1,X2,…,Xm。进攻方由n种不同类型空袭目标T1,T2,…,Tn执行一体化饱和式空袭任务,每种类型的空袭目标数量分别为N1,N2,…,Nn,并且同一类型的空袭目标编队飞行。不同防空武器对不同空袭目标的杀伤概率如表1所示。
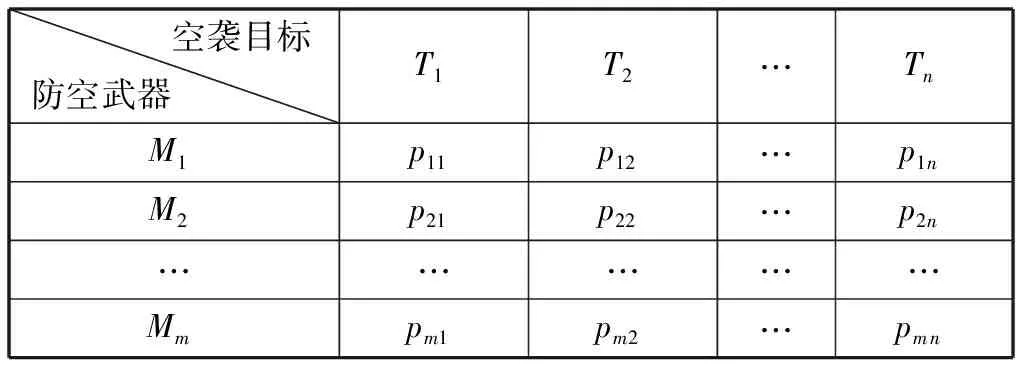
表1 各类防空武器对空袭目标的杀伤概率
不同类型防空武器对同一类型空袭目标的单个目标的拦截次数假设如表2所示。
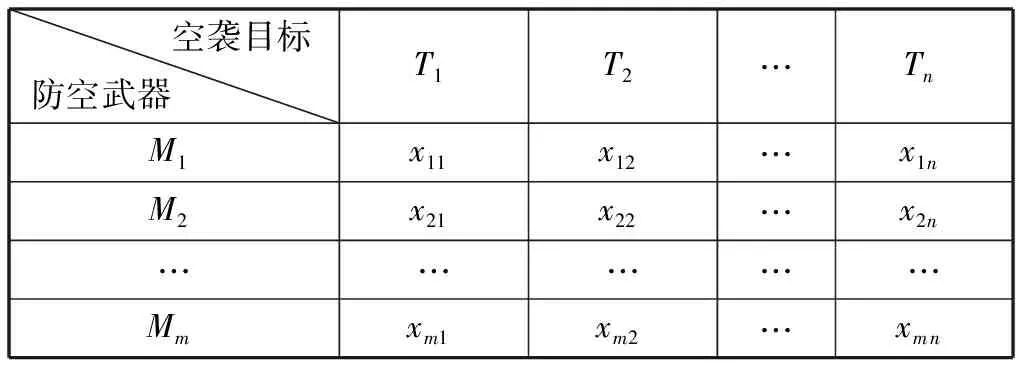
表2 各类防空武器对空袭目标的拦截次数Tab.2 The interception numbers of air defense weapons against air strike targets
1.2 单类型空袭目标突防建模
某一类型防空武器Mi对1个某一类型空袭目标Tj的杀伤概率为pij,进行xij次拦截。该空袭目标存活概率为(1-pij)xij,被摧毁概率为1-(1-pij)xij,其状态转移矩阵为
(1)
Nj个某一类型空袭目标Tj分别经过某一类型防空武器Mi的xij次拦截后,空袭目标存活数量随机变化类似马尔科夫过程[4],其状态转移矩阵为
(2)
式中,Zr,s表示r个某一类型空袭目标Tj经过某一类型防空武器Mi的xij次拦截后存活数量为s个的概率。空袭目标存活数量概率随机变化满足二项分布,其计算公式为
(3)

1.3 多类型空袭目标突防建模
按照1.2节的计算方法,n种不同类型的空袭目标T1,T2,…,Tn,分别经过m种不同类型的防空武器M1,M2,…,Mm的拦截后,每种类型空袭目标的突防概率分别为1-A01×A11×…Am1×e1,1-A02×A12×…Am2×e2,…,1-A0n×A1n×…Amn×en。
若空袭目标T1,T2,…,Tn的威胁值分别为W1,W2,…,Wn,则敌方全部类型空袭目标的总体突防威胁值计算公式为
f1=W1(1-A01×A11×…Am1×e1)+W2(1-A02×A12×…Am2×e2)+…+Wn(1-A0n×A1n×…Amn×en)
(4)
若防空武器M1,M2,…,Mm的单次拦截成本分别为C1,C2,…,Cm,则防空武器总体防御成本为
(5)
1.4 拦截方案的多目标优化模型
以敌方空袭目标的总体突防威胁值最小化和防空武器的总体防御成本最小化为优化目标,建立防空拦截方案的多目标优化数学模型,即
minf1=W1(1-A01×A11×…Am1×e1)+W2(1-A02×A12×…Am2×e2)+…+Wn(1-A0n×A1n×…Amn×en)
(6)
式中,xijmin、xijmax分别是Mi型防空武器对Tj型空袭目标拦截次数xij的最小值和最大值,可根据防空武器的战技指标和部署情况进行设置。
2 多目标优化算法
2.1 多目标优化
2.1.1多目标优化问题
多目标优化问题由决策变量、目标函数、约束条件3个部分组成,数学表达为[5]
minf(x)=[f1(x),f2(x),…,fn(x)](n=1,2,…,N)
(7)
s.t.
式中:x为决策变量;f(x)为目标函数;D为决策变量数量;N为目标函数数量;g(x)为不等式约束条件;h(x)为等式约束条件;xd_max和xd_min为决策变量的上下界。
2.1.2Pareto优化定义
Pareto优化是一种对多目标优化问题解集的比较评价方式,通过多目标优化算法求解多目标优化问题的过程是寻找Pareto解集的过程[6]。Pareto优化概念的相关定义如下:
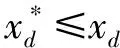
定义2:当f(x*)与f(x)满足以下条件,对∀n,fn(x*)≤fn(x)(n=1,2,…,N)且∃n0,fn0(x*) 定义3:当且仅当在变量可行域内不存在x,使得fn(x)≤fn(x*)(n=1,2,…,N),称x*为非支配最优解,但是绝大部分多目标优化问题都不存在全局最优解; 定义4:Pareto解集又称非支配解集,是所有非支配解构成的集合。Pareto边界是由Pareto解集对应的目标函数构成的图形,在空间中呈现为边界线或边界面。 本文采用的NSGA-II是一种基于Pareto优化理论的多目标进化算法,凭借简单、高效等优点,成为求解多目标优化问题的热门算法之一。NSGA-II由快速非支配排序、拥挤距离比较、精英保留策略、进化操作组成。 1) 快速非支配排序与拥挤距离比较 NSGA-II采用快速非支配排序,计算复杂度降为mN2[7],并采用基于拥挤距离的分布性保持方法,需要计算非支配集中个体的拥挤距离,其计算公式为 (8) 当种群全部个体完成快速非支配排序和拥挤距离计算之后,任意个体i都有两个属性:非支配层级ranki和拥挤距离Di。在NSGA-II中,先比较ranki,再比较Di。种群中任意两个个体i和j,若满足以下条件,则个体i优于个体j,优先获得保留的机会。 {ranki (9) 2) 精英保留策略 为避免父代种群中精英个体在进化迭代过程中流失,NSGA-II将父代种群和子代种群混合,进行快速非支配排序和拥挤距离比较,从中筛选精英个体进入下一代种群[8]。 3) 进化操作 NSGA-II采用模拟二进制交叉和多项式变异产生子代个体。首先,从父代种群中随机选取两个个体P1、P2,若进入交叉操作,两个子代个体Q1、Q2计算公式为 (10) 式中,β与随机数μ∈[0,1]有关,计算公式为 (11) 式中,ηc为交叉分布指数,ηc越大,交叉互换产生的子代个体与父代个体越相近。 若进入变异操作,则从父代种群中随机选取一个个体P3,变异产生一个子代个体Q3的计算公式为 (12) 式中:随机数r∈[0,1];xmax和xmin分别为变量x的上下限;ηm为变异分布指数,ηm是自定义参数,与ηc一样,可以根据具体进化情况进行调整。 4) 算法流程 NSGA-II的算法流程基本步骤如下: ① 随机初始化产生规模为N的第一代父代种群P1,由P1交叉互换产生规模为N的第一代子代种群Q1,将P1和Q1合并组成规模为2N的第一代混合种群R1,进入②; ② 对第t代混合种群Rt进行快速非支配排序和拥挤距离比较,从中筛选N个个体组成第t+1代父代种群Pt+1,由Pt+1交叉互换产生第t+1代子代种群Qt+1,进入③; ③ 判断是否满足进化终止条件,若满足则退出进化,若不满足则进入④; ④ 将Pt+1和Qt+1合并组成规模为2N的第t+1代混合种群,循环进入②。 本文以一个由远程、中程、近程3种防空武器混合部署构成的防御体系和由低空巡航导弹、中空制导弹药、高空作战飞机组成的空袭体系为例,对面向多层次饱和式空袭模式的拦截方案进行多目标优化设计,以同时实现空袭目标总体突防威胁值最小化和防空武器总体防御成本最小化。 不同类型防空武器对不同类型空袭目标的杀伤概率、空袭目标数量、空袭目标威胁值如表3所示。 表3 防空武器和空袭目标输入参数Tab.3 The input parameters of air defense weapons and air strike targets 远程防空武器、中程防空武器、近程防空武器的单次拦截成本分别为200万元、100万元、50万元。根据防空武器混合部署的实际情况,确定不同类型防空武器对不同空袭目标的最大拦截次数。本算例作如下假设:远程防空武器对低空巡航导弹、中空制导弹药、高空作战飞机的最大拦截次数分别为1次、2次、3次;中程防空武器对低空巡航导弹、中空制导弹药、高空作战飞机的最大拦截次数分别为2次、2次、2次;近程防空武器对低空巡航导弹、中空制导弹药、高空作战飞机的最大拦截次数分别为1次、1次、1次。 根据式(6),建立防空武器拦截方案的多目标优化数学模型,采用NSGA-II多目标进化算法求解。NSGA-II算法参数设置为:最大进化代数200,采用模拟二进制交叉和多项式变异的遗传操作,交叉参数ηc=20,交叉概率Pc=0.9,变异分布指数ηm=20,变异概率Pm=0.1。计算结果如图1所示。 如图1所示,根据防空武器拦截方案多目标优化的Pareto解集,可以获得远程防空武器、中程防空武器、近程防空武器分别对低空巡航导弹、中空制导弹药、高空作战飞机的优化拦截次数,以及相应的空袭目标总体突防威胁值和防空武器总体防御成本。由于篇幅有限,选取图中部分Pareto解集的结果进行分析,如表4所示,其中T1、T2、T3分别表示防空武器对低空巡航导弹、中空制导弹药、高空作战飞机的拦截次数。 图1 防空拦截方案的多目标优化结果Fig.1 Multi-objective optimization results of air defense interception scheme 解集序号远程防空武器中程防空武器近程防空武器T1T2T3T1T2T3T1T2T3突防威胁值防御成本(万元)11232121112.7005185021122221103.0618150030122221114.0489135040112221116.4767115050112221108.35981100601122210010.52241050701121211012.61191000801121200025.0535900900221101025.90278501000212010025.99057501100121101131.18127001200111111134.43046501300111011144.55005501400111001163.66505001500011111169.60004501600110010177.355040017001100000107.030030018001000100117.1700250 由表4可知,随着防空武器总体防御成本逐渐下降,空袭目标总体突防威胁值逐渐上升。根据图1可知:当空袭目标总体突防威胁值f1从2.70缓慢增长至12.61时,防空武器总体防御成本f2从1 850万元快速下降至1 000万元;而当空袭目标总体突防威胁值f1从25.90快速增长至117.17时,防空武器总体防御成本f2从850万元缓慢下降至250万元。因此,工程人员可根据Pareto解集的变化,选择空袭目标总体突防威胁值小幅增长、总体防御成本大幅下降的拦截方案。基于多目标优化的防空武器拦截方案设计方法,能提供多种满足约束条件、总体突防威胁值最小化和总体防御成本最低化的解集,实际工程应用中可根据自身需求进行选择。 此次算例仿真主要是为了验证防空武器拦截方案多目标优化模型和NSGA-II多目标进化算法的应用,实际工程中可以根据实际情况更改空袭目标规模、种类、威胁值以及防空武器的规模、种类、杀伤概率、拦截次数、拦截成本、约束条件等参数。 本文建立了多种不同类型空袭目标通过多种防空武器混编防御体系的突防模型;构建了以总体突防威胁值最小化和总体防御成本最小化为目标的防空武器拦截方案多目标优化模型,并采用NSGA-II多目标进化算法进行求解。仿真结果表明,基于多目标优化的防空武器拦截方案提供了多种满足约束条件的优化设计方案,可根据自身需求选择合适的拦截方案,在提高防空体系作战效能和抗饱打击能力的同时,降低总体防御成本,为实际工程应用提供一定的借鉴和参考。2.2 NSGA-II多目标进化算法

3 算例仿真

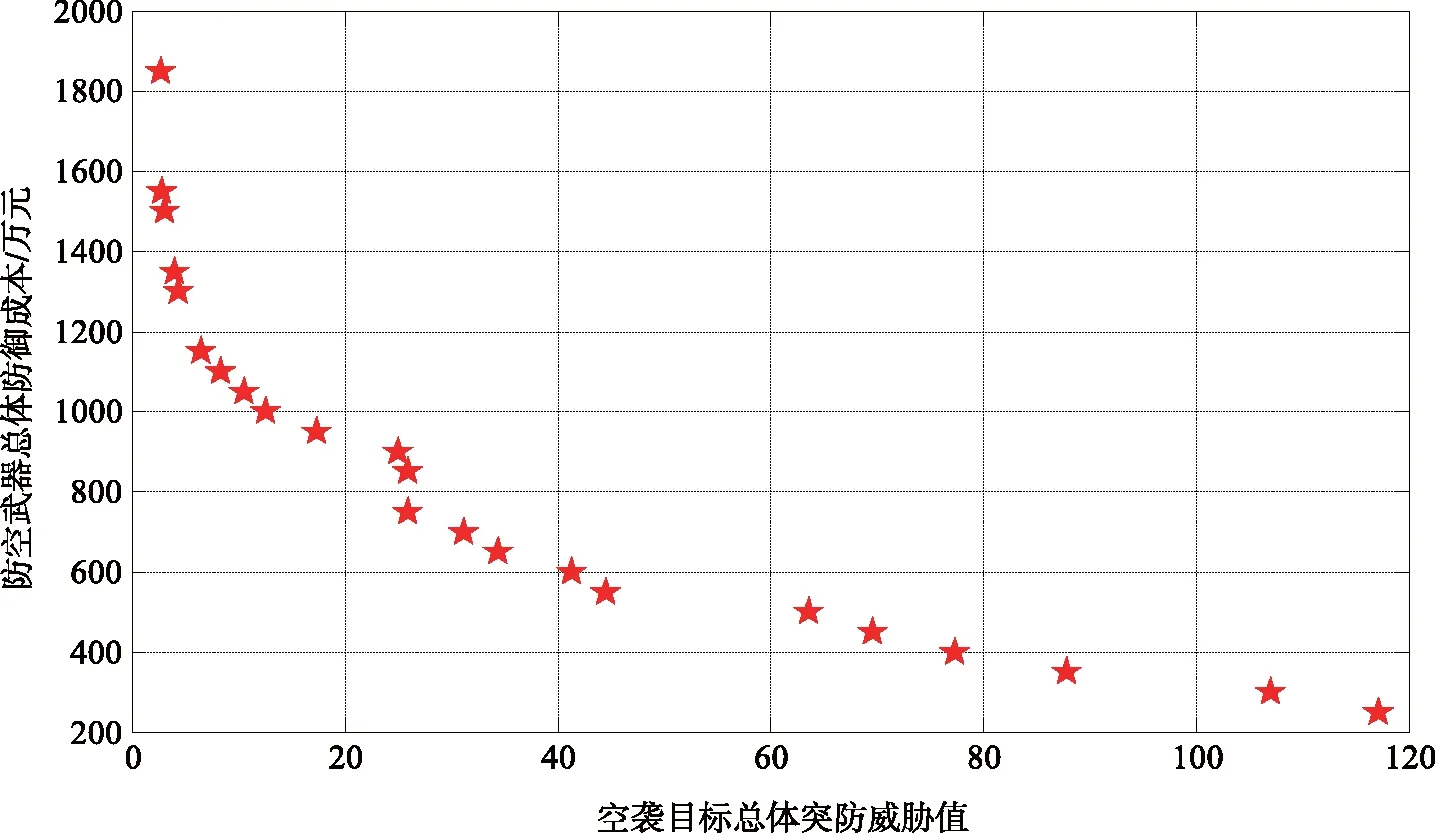
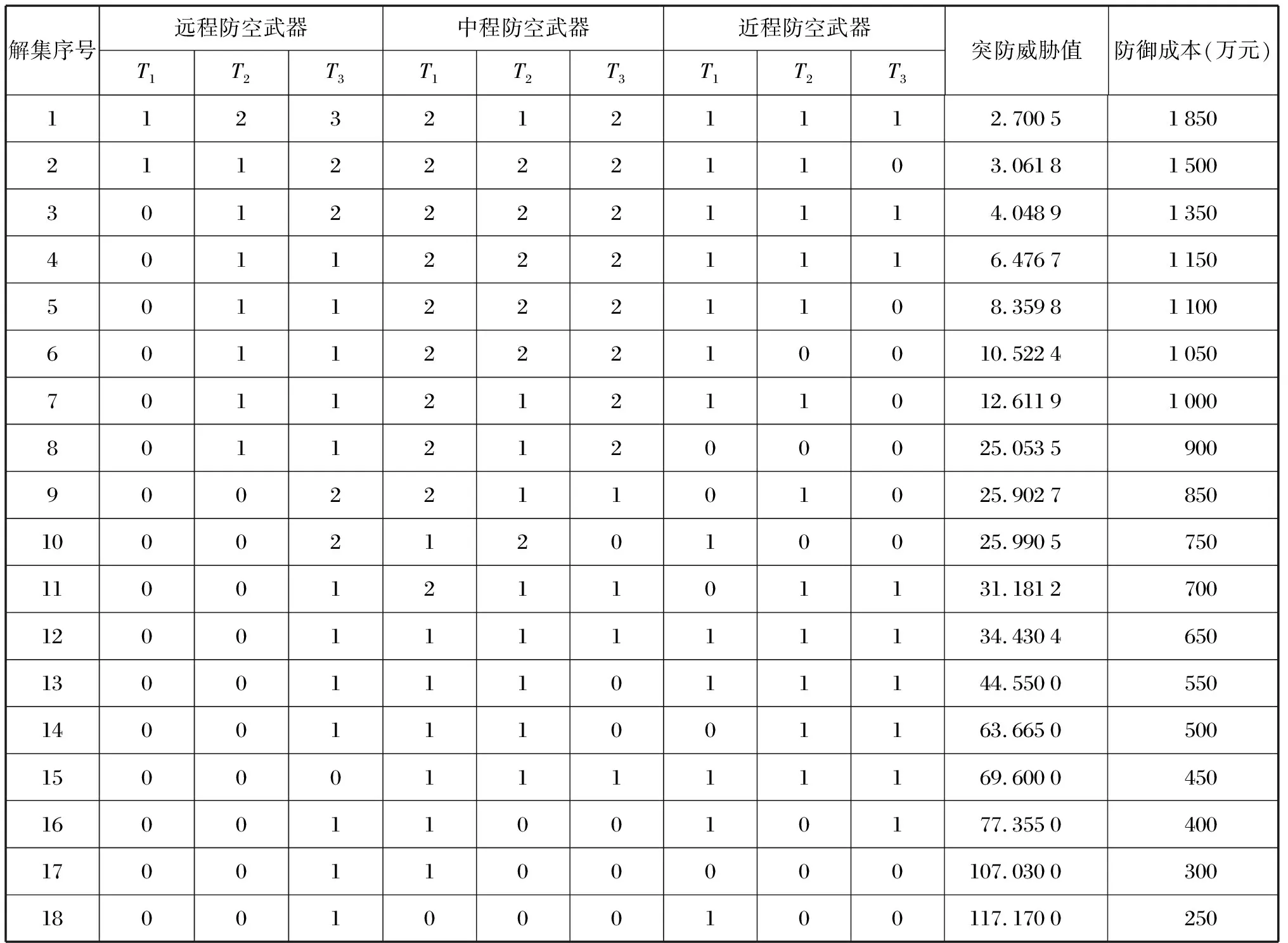
4 结束语
