基于微波成像的角锥喇叭天线宽带电磁散射特性研究
2019-12-18杨元胜朱逸飞
杨元胜,陆 波,李 晨,崔 璨,朱逸飞
(上海机电工程研究所,上海 201109)
0 引 言
未来战场上合成孔径雷达(synthetic aperture radar,SAR)应用广泛,因此对目标一维及二维像等目标特性的研究成为SAR图像能够进行有效目标识别的关键。随着电子战技术的快速发展,各种用途的天线成为各个攻击目标的主要强散射中心。因此,对天线目标电磁散射特性的研究成为研究攻击目标电磁散射特性的关键。
天线散射场的成分要比普通散射体散射场成分复杂得多,因此分析它的散射机理较为困难。对天线散射特性的研究主要是为了降低雷达散射截面积(radar cross section, RCS)以满足隐身的要求,这也使它成为未来电子战中面临的一个难题。天线作为加载散射体,其散射场一般认为包括两个部分:一部分是与散射天线负载无关的结构项散射场;另一部分则是随天线负载变化的天线模式项散射场。结构项散射场是入射平面波在天线结构上所激发的感应电流或位移电流所产生的散射场;模式项散射场是因负载与天线不匹配而经天线再辐射产生的散射场。以往对天线散射特性的研究主要集中在对窄带散射特性的研究[1-3],而近年来宽带散射特性方面的研究逐渐增多[4-5]。
喇叭天线作为一种宽频带天线有着广泛的用途,当它受远离轴向入射波照射时,几乎只存在结构项散射场;而当它受近轴方向入射波照射时,不仅会存在结构项散射场,还存在相当强度的模式项散射场。目前在喇叭天线散射特性方面的研究并不多,文献[4]通过实验测量喇叭天线的散射,确定了喇叭天线结构项和模式项散射。
基于上述背景,本文采用宽带电磁波照射短路状态的喇叭天线,得到其散射场的一维散射成像,并对喇叭天线散射场的结构项与模式项进行了分离,提取出喇叭天线的散射中心分布,得到了其散射中心分布特征;分析了喇叭天线的散射机理,并通过观察波导长度和电磁极化对散射场的影响加以验证;得到了更具有整体性的二维成像,为喇叭天线RCS减缩的研究提供了基本依据。
1 理论分析
1.1 天线的散射机理
天线的散射属于加载散射体散射,其总散射场由结构项散射场和模式项散射场两部分构成。以终端短路为参考的天线散射电场公式[6]、以终端阻抗等于天线共轭阻抗为参考的天线散射电场公式[7]均已知,根据COLLIN在文献[6]中得到的短路参考公式,可以得到终端与传输线特征阻抗相匹配的天线散射电场计算公式,即以结构项为参考的计算公式[8],为
(1)
简化为
Es(Zl)=Es(Zc)+Ea(Zl)
(2)



(3)
这样就得到了天线的模式项散射场。

图1 喇叭天线的传输线模型Fig.1 Transmission line model of the horn antenna
1.2 微波成像原理
高频区,目标的电磁散射可以等效为多个散射中心电磁散射的合成。微波成像的本质是一个求逆过程,根据接收的散射信号来反推目标各散射中心位置和强度的分布。求逆的数学变换可以是一维的,也可以是二维的,对应一维成像和二维成像,分别得到目标散射中心随一维或二维空间的分布图像。
1.2.1一维成像原理
当雷达波的距离分辨单元远小于目标的尺寸时,目标占据多个距离单元,形成了一幅目标距离图像,对目标宽频带散射数据进行逆傅里叶变换就可以得到目标散射中心在目标距离上的投影分布,即目标的一维距离像。散射场与一维距离像之间的关系[8]为
(4)
式中:Es(f)为不同频点下的散射场;f为电磁波的频点;c为光速。
1.2.2二维成像原理
相比于一维成像,二维成像过程更为复杂。在一维成像的基础上,还需通过扫角获得目标散射中心在方位向上的投影分布。因而,目标的二维像能够反映其在两维方向上精细的散射特征。散射场与二维像之间的关系[9]如式(5)所示。
(5)
式中:E为不同角度、不同频点下的散射场;φ为电磁波的发射角度。
2 仿真结果分析
为了获得喇叭天线在近轴方向的宽带散射特性,利用FEKO软件,使用快速多极子方法(multilevel fast multipole method,MLFMM)对一个工作在X波段的标准增益喇叭天线在短路负载状态下的后向散射场进行仿真计算。
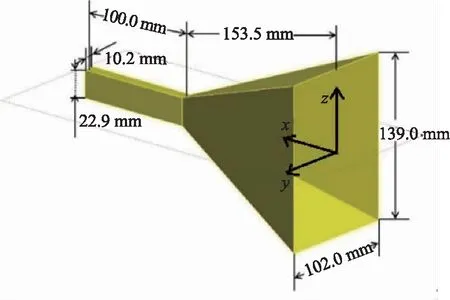
图2 喇叭天线的结构Fig.2 Structure of horn antenna
喇叭天线的结构如图2所示。接在喇叭开口面的负载端的传输线使用工作在X波段的标准波导BJ-100。这是一种标准增益喇叭天线,其他宽频带喇叭可以此为基础。
为研究喇叭天线近轴方向的宽带散射特性,FEKO软件中求解参数的设置如下:扫频区间为8~12 GHz,频率间隔为0.08 GHz;扫角区间为俯仰角θ=90°,方位角φ=-20°~20°,角度间隔为1°,φ=0°时入射平面波平行于开口面轴向;入射平面波激励与天线极化状态匹配;天线剖分尺寸为λ0/6=5 mm,共5 916个剖分单元。以MLFMM方法求解,计算远场单站后向散射电场。对φ=0°方向的散射数据进行一维成像,对φ=-20°~20°之间的散射数据进行二维成像。
2.1 一维散射成像
利用喇叭天线的宽频特性可以对其进行一维成像,将照射波方向的坐标原点置于喇叭口径面处,这样能够更加方便地对照散射中心的位置与喇叭天线模型的位置。一维成像利用快速傅里叶逆变换,从散射强度频域的数据得到时域的数据,进而得到距离的数据,从而直观地看到散射中心。由于得到的频域数据不是无限长,而是进行了截断,所以会存在能量泄露与混叠,需要加窗函数来调整。本文仿真中加Kaiser窗函数,窗系数β为55,可以有效地减少能量泄露,并综合满足对散射中心点的主瓣宽度和旁瓣高度的要求。
2.1.1无传输线情况下的一维成像
当负载为短路状态时,天线处于失配状态。由式(1)可知,此时天线同时存在结构项散射场和模式项散射场,并可知接匹配负载时,Γl=0,从而得到天线的结构项散射场。再用失配时的总散射场减去结构项散射场,可得到失配时天线的模式项散射场。总场、模式项与结构项一维像见图3。
图3中:点a、b、c表示结构项散射中心;点A、B表示模式项散射中心。结构项散射中心b、c主要源于喇叭颈部发生电磁场高次模式的反射[9],而模式项源于负载端不匹配造成的反射。此时天线的终端位置与天线颈部位置重合,导致结构项散射中心b、c和模式项散射中心A在喇叭的终端重合,无法直接通过总散射场一维成像得到分离的结构项与模式项。可以引入一个10 cm波导传输线使两位置分离。

图3 无传输线短路情况下的一维像Fig.3 One-dimensional image without short circuit of the transmission line
值得注意的是模式项散射中心B的存在,它是由于在终端到口径面的电磁波发生反射而产生的。本文通过对电磁波辐射数据进行一维成像来验证,得到图4。从图4中可以看到除了散射中心A以外,也有散射中心B的存在,这就证明在口径面处发生了反射。
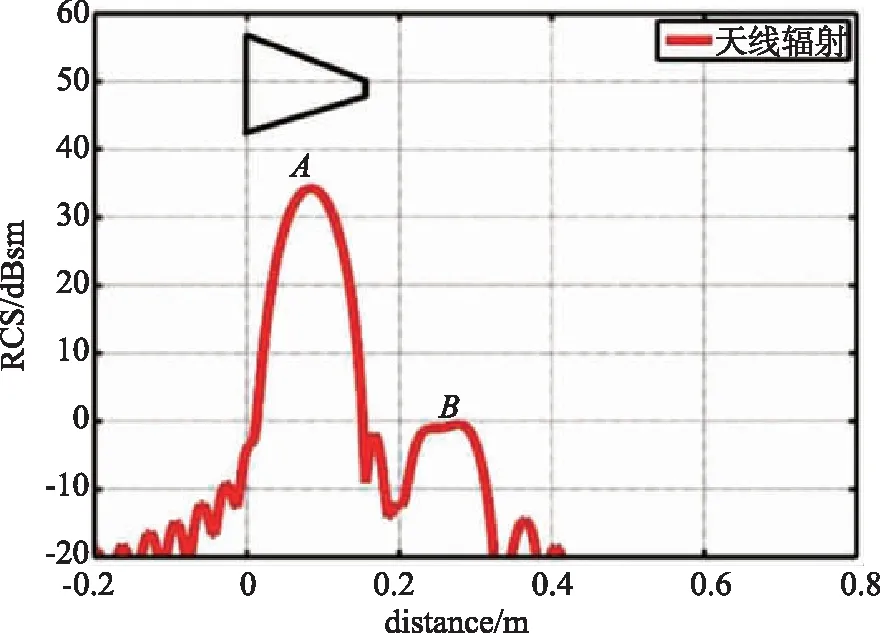
图4 喇叭天线辐射的一维像Fig.4 One-dimensional image of the horn antenna radiation
2.1.2有传输线情况下一维成像与散射项分离
根据上文所述,可以通过加10 cm的传输线实现对失配天线散射场的分离。先对终端短路10 cm的传输线进行散射成像,以便对加传输线的角锥喇叭有更深的认识。10 cm传输线的一维散射成像如图5所示。从图5、表1和表2可以看出,矩形波导口径面处有一个散射中心,类似于天线的结构项散射中心,与天线终端的情况无关。根据文献[11]可知a散射中心是由于电磁波的绕射产生的。
在匹配的情况下不存在模式项的散射,也就是此时的结构项。在短路时,由于严重失配,出现了模式项散射。A、B、C为3个主要的散射中心。模式项相比结构项较为复杂,根据图5和表1可以总结为以下两个特点。
1) 主散射中心位于喇叭终端外(口径面与波导终端距离为0.253 5 m,小于0.288 0 m);
2) 次散射中心位置逐渐远离终端,并且散射强度递减。
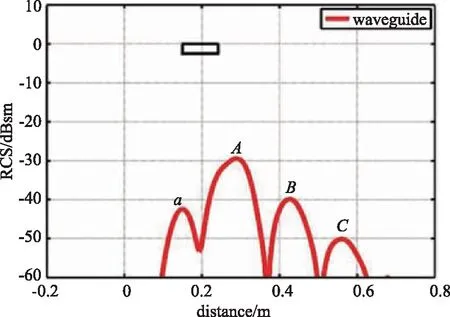
图5 波导传输线短路状态下的一维像Fig.5 One-dimensional image with short-circuit of waveguide transmission line
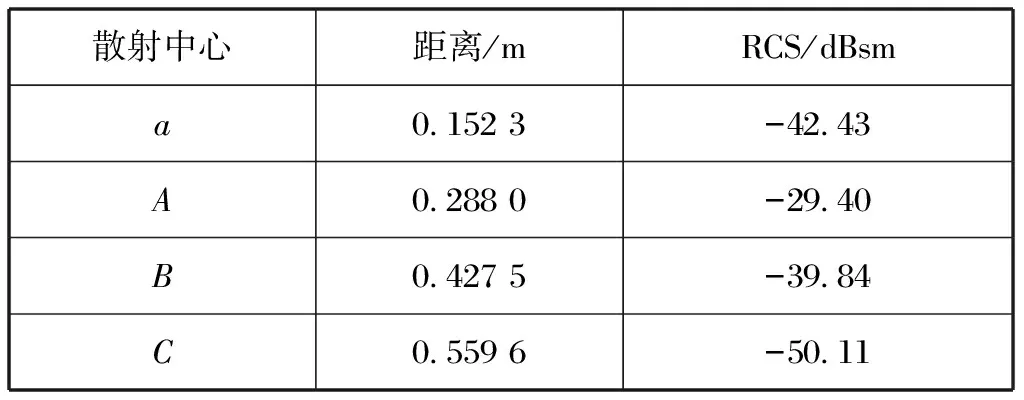
散射中心距离/mRCS/dBsma0.152 3-42.43A0.288 0-29.40B0.427 5-39.84C0.559 6-50.11

表2 波导传输线短路状态下模式项散射中心距离差与强度差Tab.2 Mode scattering center distance and intensity difference with short-circuit of waveguide transmission line
关于模式项的特性,以往的文献研究较少。根据模式项的计算式(3),可知其与天线反射系数Γa和负载反射系数Γl密切相关。分析上面两个特点要从这2个反射系数入手。短路使得Γl确定,模为1。波导与自由空间不匹配,反射系数Γa为一个复数,透射系数也为一个复数,所以电磁波经过矩形波导到自由空间交界处的过程被加入了一个相位的延迟,体现到散射中心,就使得散射中心位于终端外。
另外,Γa的模小于1,电磁波每次从交界处反射的回波强度会降低,且经过的距离增加0.2 m。但由于波导内电磁波传播速度为空气中传播速度的1/G(G为波导色散因子),所以时延为空气中的G倍,相当于在空气中经过的距离增加0.2×G。当频率为8~12 GHz时,该矩形波导的G值为0.57~0.84,所以再反射电磁波每次经过的距离均增加0.2×G,即0.114~0.168 m,由此可得模式项散射中心相互距离的范围为0.114~0.168 m。仿真结果约为0.13 m,在此范围内,说明次散射中心位置逐渐远离终端,并且散射强度递减。
在对波导传输线散射特性进行研究的基础上,对加0.1 m传输线的终端短路的角锥喇叭天线进行一维微波成像,如图6所示。从图6和表3可以看出,通过加传输线可以将喇叭天线的结构项和模式项散射中心在距离上进行分离。点a、b、c为结构项散射中心,a是由于电磁波的绕射产生的,b、c是由于喇叭天线颈部的高次模式反射产生的,都与终端无关。
点A、B、C是天线的模式项散射中心,其特点与只有波导传输线的模式项散射中心特点相同,只不过Γa的产生原因是由于波导与天线的不匹配。但是需要注意的是,由于前置角锥喇叭的影响,距离差与RCS的强度变化量均不及只有传输线时均匀。正如2.1.1所讨论的那样,在喇叭的口径面也会有一定的反射,可能会与波导、天线交界面的反射波发生混叠,造成散射中心不均匀。
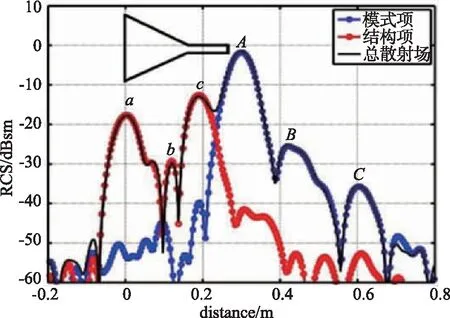
图6 加0.1 m传输线的短路状态下的一维像Fig.6 One-dimensional image with short-circuit of adding 0.1 m transmission line

散射中心距离/mRCS/dBsma0.005 5-17.770b0.122 9-29.740c0.185 3-12.980A0.299 0-1.568B0.416 5-25.320C0.603 6-35.650
2.1.3波导长度对一维成像的影响
为了验证上述结论,将0.1 m与0.2 m波导长度下的一维像作对比,如图7和表4所示。A1、B1、C1、D1为0.1 m波导长度的模式项散射中心,A2、B2、C2、D2为0.2 m波导长度的模式项散射中心。由图7可知,B1和A2位置接近,D1和B2位置接近,且A1、B1的强度分别与A2、B2的强度接近,从而可以验证模式项散射场因多次反射而产生多散射中心的想法。
终端不匹配造成再辐射,是模式项散射产生的原因。交界处的不匹配,使得出波有一定相位延迟,造成了主散射中心在终端外;回波产生多次反射,使得次散射中心逐渐远离终端,散射强度递减。
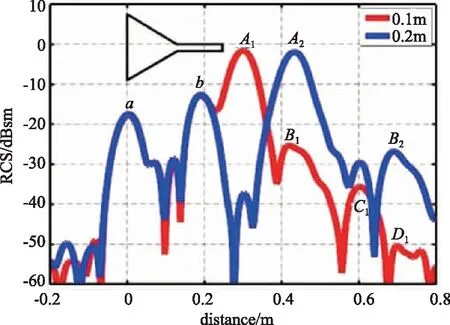
图7 不同传输线长度的一维像Fig.7 One-dimensional images of transmission lines with different lengths
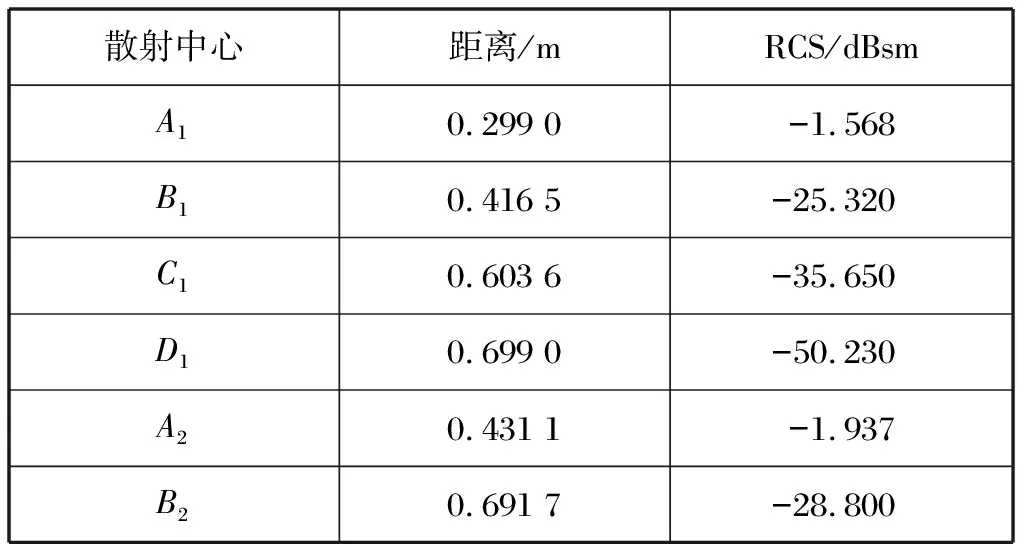
散射中心距离/mRCS/dBsmA10.299 0-1.568B10.416 5-25.320C10.603 6-35.650D10.699 0-50.230A20.431 1-1.937B20.691 7-28.800
2.1.4极化正交对一维成像的影响
以上研究的内容均为天线与电磁波极化匹配的情况,还要研究极化正交的情况才能完整地展示角锥喇叭天线的散射特性。
由图8可以看出,当极化正交时,天线的结构项散射强度将会增大,而模式项散射几乎消失。因为相比极化匹配的情况,在天线与波导交界处,不但高次模式被反射回去,而且主模也因低于TE01的导通频率而被反射回去,这就使得结构项散射强度增大,模式项散射消失。终端匹配和极化正交虽然都会使得模式项消失,但是原理却不一样,终端匹配是进入波导的电磁波没有被反射,极化正交是电磁波根本无法进入波导之中。
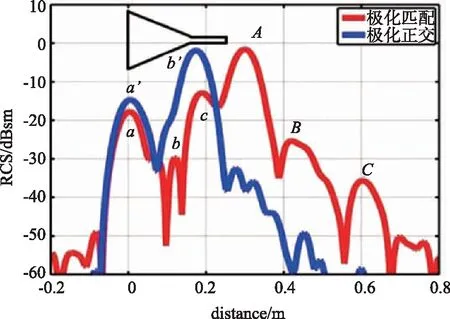
图8 不同极化方式的一维像Fig.8 One-dimensional image of transmission line with different polarizations
2.2 二维散射成像
对飞行器隐身性能的研究一般都是对其进行二维散射成像,对其天线也采用二维成像方法,使之符合飞行器整体的RCS缩减需要。对天线的二维散射中心与飞机整体的二维散射中心进行综合考虑,如散射中心相同、相位相差180°,则整体的隐身效果达到最好,并且二维散射成像会使散射中心更加直观、形象地呈现出来。
图9~11显示了加传输线的角锥喇叭天线短路状态下总散射场和分离得到的结构项与模式项散射场,二维像与一维像对应,结论与一维像相同,但是忽略了次散射中心,仅展示出主散射中心,对于散射机理的理解更加清晰。
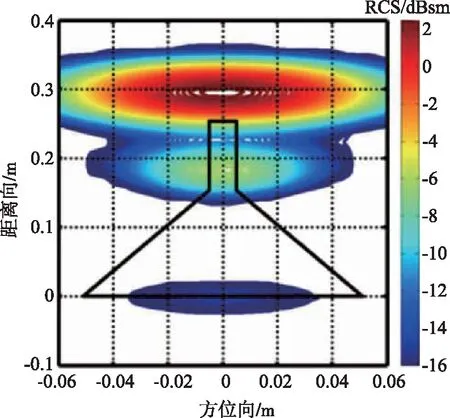
图9 总散射场的二维像Fig.9 Two-dimensional image of the total scattering field
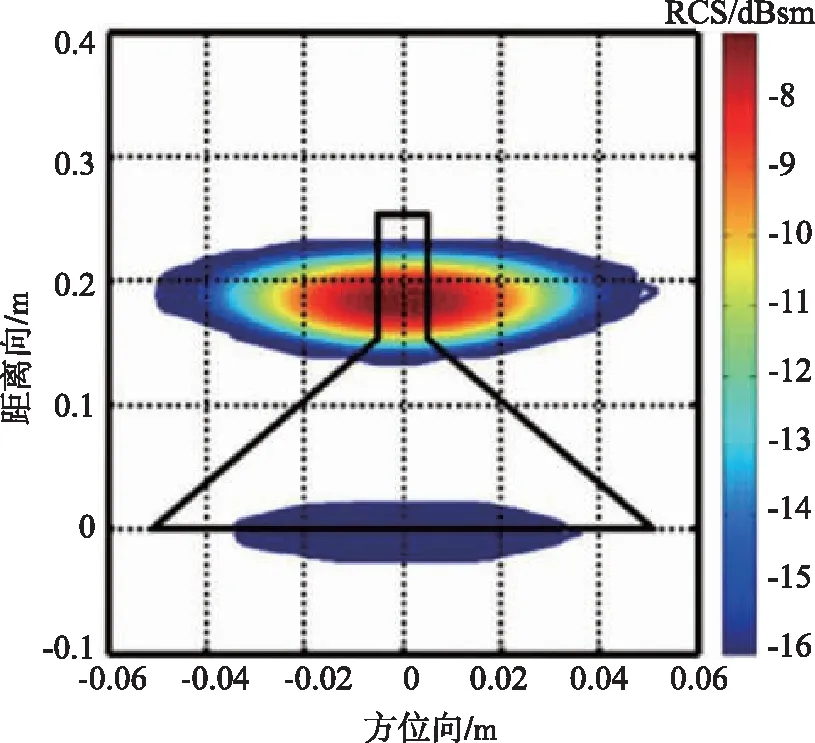
图10 结构项散射场的二维像Fig.10 Two-dimensional image of the structural scattering field
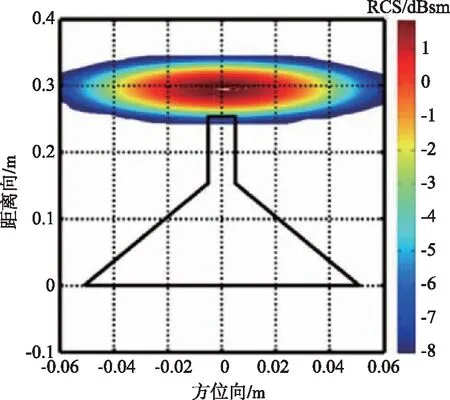
图11 短路状态下模式项散射场的二维像Fig.11 Two-dimensional image with short-circuit of the mode scattering field
3 结束语
本文对角锥喇叭天线的近轴散射特性进行了研究,得出如下结论:
1) 喇叭天线的散射场可以通过散射成像分离为模式项与结构项;
2) 结构项散射中心位于天线的口径面处和喇叭与波导的交界处,分别源于天线口径面的边缘绕射和交界处的高次模式反射;
3) 模式项的主散射中心在终端外,次散射中心依次远离终端,并且散射强度递减;
4) 极化正交时,天线的结构项散射强度将会增大,而模式项散射几乎消失。
本文所研究的标准喇叭天线具有很强的代表性,可为以后对宽带天线的散射特性研究提供帮助,并且对其进行了一维、二维的散射成像,为其RCS减小提供了理论基础。
