基于优化SPOT和D-S证据理论的测试性验证方案
2019-12-09王康史贤俊周绍磊龙玉峰孙美美
王康,史贤俊,周绍磊,龙玉峰,孙美美
海军航空大学,烟台 264001
经典的验证试验设计、参数估计与检验方法主要以大样本试验为前提而开展的,但是对于导弹这类高精度武器系统而言,由于其高昂的造价致使投入使用的样机较少,试验周期较长,导致实际开展验证试验时样本量受到小子样条件限制[1]。
随着试验方法的多样化、系统仿真技术的成熟化,使得在验证试验开展前具备多源先验信息,包括同类武器系统的历史试验信息、专家基于武器装备水平认知的经验信息及预计信息、武器装备研制过程中各层级的试验信息及仿真试验信息等[2]。可见,多源信息融合技术的运用就成为基于小子样条件下验证试验的核心环节。
由于Bayes方法能够充分运用各种已有的先验信息,可在小子样条件下对导弹等高精度复杂装备系统的统计推断做出可信度较高的估计,故Bayes方法在不同工程领域(如可靠性[3]、维修性[4]以及测试性[5]等)、不同的应用背景(如验证试验设计[6]、参数估计[7]与检验[8]等)中得到了广泛的应用。
在Bayes方法的验证试验设计方面,通过在序贯试验设计方案中引入Bayes方法来融合相关先验信息,得到了国内外广大研究者的青睐。考虑简单假设条件,文献[9]基于成功率序贯抽样方法,将产品研制阶段获得的数据转化为等效的实际数据,利用贝叶斯统计公式将等效的实际数据融合为真实的验证测试数据,能有效地降低现场验证试验样本量;文献[10]基于二项分布模型推导了Bayes截尾序贯概率比检验(SPRT)方法,证明该方法能充分运用先验信息,得到其平均试验样本量优于传统SPRT方法,适合于小子样条件下的验证试验设计。考虑复杂假设条件,文献[11]充分结合SPRT方法和Bayes方法的优点,提出一种序贯验后加权检验(SPOT)方法,能充分运用先验信息,达到减少验证试验样本量的目的;文献[12]针对二项分布模型的测试性验证试验方案的制定,利用SPOT方法通过序贯后验概率比和决策阈值实现样本量的动态判决,在相同约束参数下证明SPOT方法的实际样本量要优于SPRT方法,达到减少样本量的目的。无论是考虑简单假设亦或复杂假设,均未能考虑原假设和备择假设间的模糊参数空间,当实际指标值位于模糊参数空间时会导致较高的误判率,所需样本量也会相应增加。
针对模糊参数空间的处理问题,文献[13]以导弹命中概率为研究对象,通过MSPOT方法有效考虑了最低可接受值和设计指标值之间的模糊参数空间处理问题;文献[14]提出了多简单假设的MSPRT方法,并考虑了先验信息,研究了试验风险与试验样本量期望值的估计方法。以上分别针对多简单假设和多复杂假设条件下的模糊参数空间的问题,但未能将序贯试验设计的具体过程作为研究重点,同时未能充分运用多源先验信息。
鉴于此,综述相关文献,一方面目前融合先验信息的序贯试验设计方案未能在测试性验证领域得到充分应用,另一方面现有研究测试性验证试验设计的文献亦未能考虑测试性指标之间的模糊参数区间以及多源先验信息的问题。针对模糊参数空间的问题,本文以测试性承制方要求值和使用方要求值构建三参数空间复杂假设,并基于Bayes方法研究序贯试验设计的具体过程,包括决策因子和决策阈值的确定,以及基于Bayes理论研究序贯决策规则;针对多源先验信息的问题,本文以测试性指标构成的参数空间为辨识框架,基于D-S证据理论融合测试性专家信息以及测试性试验数据。两者结合起来,提出一种基于优化SPOT和D-S证据理论的测试性验证试验方案(下称优化DS-SPOT方案),在保证测试性验证样本充分性和试验结果置信度的同时,旨在充分利用先验信息解决工程应用中测试性验证试验受费用的限制性和故障样本量注入的困难性,期使在实际工程应用中达到优化验证试验样本、缩短试验周期,降低试验费用的问题。
1 问题描述
设p0为承制方测试性水平要求值,p1为使用方测试性水平要求值(p0>p1),则测试性指标参数空间Θ可以划分为3部分Θ={Θ0,Θ1,Θ2},其中Θ0={p:p≥p0},Θ1={p:p1 (1) 同时假设n次测试性验证试验结果序贯序列表示为X={X1,…,Xi,…,Xn},Xi={0,1},Xi=1表示验证试验成功,Xi=0表示验证试验失败,记c为n次试验结果序贯序列中Xi=0的个数,即表示累积验证失败次数。在采用Bayes方法进行统计分析时,通过武器系统历史试验信息以及装备各层级试验信息等得到测试性指标的先验分布为π(p),结合序贯序列X可以得到验后分布π(p|X),则传统SPOT方法给出的序贯后验概率比可表示为[15] (2) 根据On(X)和决策常数A和B的动态比较即可完成测试性验证试验的接收/拒收判定,决策常数A和B可表示为[15] (3) 问题2两假设的复杂假设问题仅考虑了测试性指标参数是否被接收/拒收,当指标参数p∈Θ1时,两假设检验问题的验证方案无法做出判断,会判给Θ0或者Θ2,直接导致风险απ0和βπ1增加;同时,未能从“小概率事件原理”[16]的角度解释接受/拒收原假设,即未能给出接受/拒收原假设的后验概率值。 问题3对导弹类高精度武器装备开展测试性验证试验前,其研制阶段存在专家信息以及成败型试验信息等多源测试性先验信息,这些先验信息反映了装备在不同研制阶段的测试性水平,如何运用这些先验信息对先验分布π(p)进行有效补充,并合理制定装备的测试性验证方案也是问题之一。 论文将模糊参数空间纳入假设检验中,构造测试性指标的三参数空间复杂假设: H0:p≥p0,H1:p1 (4) 针对问题1,重新定义各假设的验前概率为 (5) 式(5)中π(H0)+π(H1)+π(H2)=1,考虑承制方和使用方要求值间的模糊区域,保证了指标空间划分的完备性。 针对问题2,考虑传统SPOT方法中仅做出接受/拒收判决以及未能从“小概率事件原理”的角度解释接受/拒收原假设的问题,制定三参数空间复杂假设的决策规则,实现对测试性真实指标所属参数空间的有效判定。 设测试性指标参数p的先验分布服从Beta分布,则有: (6) 式中:a和b表示先验分布的超参数。 根据验证试验序贯序列X={X1,X2,…,Xn}得到的(n,c)值,由Bayes公式可得的后验分布具备如下形式: π(p|(n,c))= Beta(p;a+n-c,b+c) (7) 则通过式(7)以及式(5)可计算出假设Hi(i=0,1,2)成立的后验概率为 (8) 据此,可以建立三参数空间复杂假设的Bayes序贯检验决策规则。 1) 决策因子 为了建立Bayes序贯检验决策规则,首先对后验概率π(Hi|(n,c))进行分析,根据式(8)有 (9) 基于式(9)给出决策因子的定义为 (10) 从式(10)中可以看出,决策因子Λi(X)相对于传统SPOT方法的序贯概率比On(X)(见式(2))而言,将待测指标模糊参数空间的后验概率融入进来,保证了假设检验问题的完备性。 2) 决策阈值 假设做出决策接受假设Hi时,决策因子Λi(X)的阈值上界为Ai,由于序贯验证试验过程的动态性,导致难以确定Ai确切的数学表达式,同时由式(10)知,π(Hi|(n,c))越大,Λi(X)的值越小,同时π(Hi|(n,c))越大也说明需要更加准确的先验分布和更充足的实际序贯验证数据,因此确定决策阈值Ai对于确定序贯验证试验样本量有着直接的约束作用,进而影响序贯决策的准确性。决策阈值Ai越小,相应的样本需求越大,决策结果越精确。本文基于后验概率和“小概率事件原理”,通过引入三参数空间的误判风险αHi,给出了决策阈值的确定方法,如下: ① 从“小概率事件原理”上而言,当根据实际序贯验证试验数据以及先验分布支持接受假设Hi成立时,可认为后验概率π(Hi|(n,c))具备较大的值,以此证明假设Hi的正确性。因此在接受假设Hi时,作如下要求: (11) 式中:αHi表示接受假设Hi的误判风险接受值(由承制方和使用方提供)。 ② 根据式(9)和式(10)有 (12) (13) 3) 决策规则 通过以上序贯验证试验设计分析,根据式(10)、式(11)和式(13)的约束要求,则有如下序贯决策规则: ∃i, s.t.Na=infn≥1: (14) 式中:Na表示序贯停止时的最小样本量;δ表示决策结果。 至此,完成了优化SPOT方法序贯试验的设计过程。 针对问题3,导弹装备在研制阶段的测试性信息来源广泛,包括专家信息以及成败型试验信息,而D-S证据理论在对随机不确定性问题和认知不确定性问题的表达和处理方面具备较强的能力,本文为合理有效的运用研制阶段的测试性多源先验信息,利用D-S证据理论融合多源先验信息,对第2节序贯验证试验方案进一步优化。 根据D-S证据理论的定义[17],考虑到测试性指标参数空间Θ的非空性以及Θ中元素满足互不相容的条件,因此定义辨识框架为Θ={Θ0,Θ1,Θ2},在此基础上针对多源先验信息构建其相应的基本信任分配函数m。 对于历史成败型试验信息(n,c)可视为辨识框架Θ上的一个证据,根据第2节的分析,基于式(8)可以建立该证据在辨识框架Θ的基本信任分配函数m1: (15) 在导弹武器装备的研制过程中,测试性领域专家基于其自身对导弹装备测试性水平的认知,能通过不同评估形式[18](区间估计形式以及单侧置信下限形式)给出导弹装备测试性水平的评估信息。 (16) 其次,在给定置信度水平γ1下,实现区间估计形式数据[pL,pU]向成败型数据(n′,c′)的折合: (17) 根据式(17)将区间形式的专家信息转化为成败型数据(n′,c′),据此构建区间形式的专家信息基本信任分配函数m21: (18) (19) (20) 根据式(20)将单侧置信下限形式的专家信息转化为成败型数据(n″,c″),据此构建区间估计形式的专家信息的基本信任分配函数m22: (21) 为了确定测试性序贯验证试验方案及给出序贯决策结果δ,根据序贯判决规则式(14),现假设Na次序贯验证试验后作出决策,对应的检测/隔离失败数为Ca,将该序贯验证方案(Na,Ca)视为一个证据,构建其基本信任分配函数m0: (22) (23) 式中:由于对测试性指标进行评估时,一般仅会约定一种形式的专家信息,所以基本信任分配函数m2表示m21和m22中的任意一种,具体根据所约定的专家信息的形式而决定。 定理1如果优化序贯验证方案进行到第Na次时(对应的检测/隔离失败数为Ca),满足以下条件: ∃i,s.t. (24) 则(Na,Ca)为在接受假设δ=Hi下的一次序贯验证试验方案。 证明对m0(Θ1)而言,根据第2节所设计的优化SPOT序贯试验方案,(Na,Ca)为其一次序贯方案,则根据序贯规则式(14),如若接受假设δ=Hi,则必然存在: (25) (26) (27) 显然,对于∀ε>0,总存在(Na,Ca)使得式(28)成立: (28) 同时,由于研制信息已知,则研制信息确定的m函数确定,根据D-S证据理论合成公式有 (29) 式中:Mki为常数。进一步可得: (30) 以某型导弹装备的飞控系统故障检测率(FDR)为研究对象,待验证装备的先验信息来源于历史装备的试验数据。由于历史装备已经具备较好的测试性水平,待验证装备只是在历史装备的基础上增加新的BIT(Build In Test)设计及测试性设计。在历史装备的测试性验证试验中,共注入了82次故障,正确检测故障78次,未能成功检测故障4次,采用Hart运用的经验Bayes方法[19]对历史装备信息进行处理,即认为历史装备的验证试验等价于对当前装备进行了60%次数的试验。因此可确定先验分布满足: π(p)=Beta(p;78×0.6,4×0.6)= Beta(p;46.8,2.4) (31) 同时,经承制方和使用方共同确定,承制方要求值p0=0.95,使用方要求值p1=0.90,双方风险值α=β=0.1,以及本文为实现三参数空间的Bayes序贯决策需提供的接受假设Hi(i=0,1,2)时的误判风险接受值αHi=0.1。 根据式(15)和式(21),可以得到辨识框架Θ上的各先验信息的m函数如表1所示。 表1 不同先验信息的m函数表Table 1 m function table for different prior information 4.2.1 固定抽样类测试性验证方案 1)经典测试性验证方案。依据文献[21]可得测试性验证试验方案为(187,13),实际的双方风险为α=0.087 4,β=0.098 1。 2)传统Bayes测试性验证方案。确定先验分布为π(p)=Beta(p;46.8,2.4),依据文献[22]可得传统Bayes验证试验方案为(66,4),实际的双方风险为α=0.069 7,β=0.096 2。 4.2.2 序贯类测试性验证方案 本文对飞控系统进行了2次模拟仿真验证试验,以所有方案均作出判决则停止验证试验为准则,得到各序贯类试验的试验次数,以及对应的检测失败数。 1) SPRT测试性验证方案。根据文献[23],计算得到阈值上界ASPRT=9,阈值下界BSPRT=1/9,2次模拟仿真验证如图1所示。 2) SPOT测试性验证方案。先验分布即为π(p)=Beta(p;46.8,2.4),根据文献[24]计算得到阈值上界ASPOT=79.948 7,阈值下界BSPOT=0.060 9。2次模拟仿真验证亦如图1所示。 3) 本文方案。决策阈值为A0=A1=A2=1/9,从决策因子角度给出了序贯验证过程如图2(a)和图2(b)所示,图中分别给出了不融合先验信息、只融合成败型信息、只融合专家信息以及同时融合成败型信息和专家信息的序贯决策曲线,同时也从后验概率分布角度给出了序贯决策过程,如图2(c)和图2(d)所示。 图1 SPRT和SPOT测试性验证试验序贯判决Fig.1 Sequential judgment of SPRT and SPOT testability verification test 不同序贯类方案2次测试性验证试验决策情况如表2所示。 4.2.3 结果分析 1) 结合表2的序贯决策结果,分析图1(a)和图2(a)可得,不融合先验信息的优化DS-SPOT序贯方案实际所需的样本量,比SPRT方案略少,而多于SPOT方案,3种序贯方案均优于固定抽样方案,且均接受H0:p≥p0的决策。 2) 分析图1(b)和图2(b)可得,不融合先验信息的优化DS-SPOT方案较之SPOT方案需要相对较多的样本量,这是由于本文方案从后验概率来描述决策过程,其作出决策时后验概率为0.901 7,而传统SPOT方案作出决策时后验概率为0.758 9,从后验概率而言本文方法更容易得到使用方的认可。 3) 从图2(a)和图2(b)中可以反映出通过证据理论融合专家经验信息和成败型信息后优化DS-SPOT方案均能在一定程度上减少试验所需的样本量,说明专家信息和成败型信息支持接受对假设H0的决策,且同时融合专家信息和成败型信息实际所需序贯样本量更小,2次验证试验所需样本量均优于SPOT方案、SPRT方案。同时,图2(a)和图2(b)还反映出通过专家信息和成败型信息融合后所需样本量相当,表明二者对于接受对假设H0的决策具备相当的支持度。 4) 图2(c)和图2(d)从后验概率的角度给出了优化DS-SPOT方法的序贯决策过程,表明作出决策时后验概率的取值情况,便于决策者基于“小概率原理”进行相应的决策判断。 表2 不同序贯方案决策结果 序贯方案(验证试验次数,检测隔离情况)第1次验证试验第2次验证试验决策结果SPRT方案(41,0)(55,1)SPOT方案(23,0)(40,1)优化DS-SPOT方案未融合先验信息(40,0)(68,1)融合成败型信息(29,0)(56,1)融合专家信息(28,0)(55,1)融合成败型和专家信息(18,0)(18,0)均接受假设H0 可见,本文所提优化DS-SPOT方案,一方面能很好地融合专家信息和成败型信息,相应地减少试验样本量,另一方面能从后验概率的角度作出决策,解决了传统SPOT方法作出决策时后验概率可能不大而使决策难以得到认可的不足。 上述对飞控系统的2次模拟仿真验证试验以实例的形式表明了优化方案的有效性,为了从一般层面上验证所提方案的有效性,选用序贯类验证试验的度量指标—平均样本量(ASN),对所提方案进行分析。为了保证不同方法ASN比较的合理性,首先应对方法的抽样特性进行比较,在抽样特性接近的情况下开展ASN的比较。经典验证方案和传统Bayes验证方案是基于二项分布模型的,具备相同抽样特性函数[12],可据此绘制抽样特性曲线。SPRT方案抽样特性和平均样本量的图形绘制可通过文献[25]给出的解析公式进行绘制,而SPOT方案和本文方案的抽样特性和平均样本量不具备解析解,采用Monte Carlo仿真的方式进行,具体如下: 步骤1将测试性指标划p划分为1 000个离散测试性水平值pi=0.001×i,i=1,2,…,1 000。 步骤2对于划分的1 000个离散测试性水平值进行N次判决过程试验。当测试性水平离散值取为pi时,以概率pi随机生成成败型试验数据,在第j(j=1,2,…,N)次仿真过程中,可得到作出决策的试验次数为Nij,对应的检测失败次数为Cij(对于SPOT方案而言决策即为接受或拒收,对于本文方案而言决策为判断属于假设H0,H1或者是H2);同时,作出决策且判断为接收时,则pi对应的接收判决次数Tij相应加1。 步骤3当测试性水平取值为pi时,对应的抽样特性OCi、平均抽样次数ASNi和平均检测失败次数ACi可表示为 (32) 事实上,SPOT方案和本文方案可能存在验证试验无法决策的情况,此时需要对试验方案进行截尾,本文均选用固定截尾NT=100,当样本量达到100而无法进行决策时,2种方法均根据后验概率进行决策,选择不同假设中后验概率较大者作为最终决策。 通过上述步骤和约定截尾措施,得到SPRT方案、SPOT方案以及本文方案的抽样特性、平均样本量和检测失败次数对比曲线如图3~图5所示(本文采用1∶5∶1 000的间隔步长进行绘图,避免数据点密集而图形辨识度不足的问题)。 图3 抽样特性对比曲线Fig.3 Comparison of sampling characteristics curves 图4 平均样本量对比曲线Fig.4 Comparison of average sample sizes curves 分析图3~图5可以得到以下结论: 1) 由于在整个FDR的取值区间[0,1]上,几种不同方法的OC值大多为0,为使对比更明显,图3仅显示了[0.6,1]区间内的抽样特性曲线。以经典验证方案的抽样特性曲线为参考,其余不同方案得到的抽样特性曲线相对接近。通过图3中[0.95,1]区间的局部放大图,且图3反映出在相同FDR取值pi下,未融合优化DS-SPOT方案OC值较之经典验证方案OC值差距相对最大,但融合专家和成败型信息方案的OC值与经典验证方案OC值更为接近,这是由于融合信息会增加作出正确决策Tij的次数,故相应的OC值会增加。 2) 图4和图5中给出了区间[0.95,1]的局部放大图,可以看出在该区间内融合专家信息、融合成败型信息以及同时融合专家信息和成败型信息的优化DS-SPOT方案较之未融合的方案而言具备更小的平均样本量和检测失败次数,同时通过计算当前平均样本量下的后验概率π(Hi|(ASN,AC))(i=0,1,2),总有后验概率π(H0|(ASN,AC))最大,且满足本文设计的序贯决策要求,表明了先验信息对于决策H0具备支持作用,融合能减少接受假设H0的平均样本量。 3) 无论是从平均样本量角度还是从平均检测失败数角度而言,单独融合成败型信息和单独融合专家信息在接受假设H1和H2时(区间范围为(0,0.95)),可能具备比不融合方案更多的平均样本量和检测失败数,这是由于专家信息和成败型信息是支持决策H0的,显然如果要支持对H1和H2的决策则必然需要更多的样本量,符合实际情况。同时,比较融合成败型信息的优化方案和融合专家信息的优化方案,从图4中反映出融合专家信息的优化方案较之融合成败型信息的优化方案具备相对较少的平均样本量,这说明专家信息对决策H0的支持度要高于成败型信息,这一点从图5平均检验失败数也能得到印证,支持度高的方案等同于验证试验开展前提供了相应的较多的检测成功次数,如果要接受假设H2,则必然需要更多的检测失败数。 4) 同时融合专家信息和融合成败型信息的优化方案具备比仅融合专家信息、仅融合成败型信息以及不融合先验信息方案更少的平均样本量和平均检测失败次数。在决策域H1和H2上(区间范围为(0,0.95)),通过计算后验概率π(Hi|(ASN,AC)),同时融合两者可能会使得π(H1|(n,c))≥1-αH1,即判定给模糊参数空间H1,并能从“小概率事件原理”进行合理解释,说明装备测试性水平仍有待提升。这也是造成融合专家信息和成败型信息后,对于接受假设H0的支持度提高,而在决策域H1和H2上平均样本量和平均检测失败次数却减少的原因。 5) 由于先验信息对于决策H0的支持,通过对比分析区间[0.95,1]上本文融合先验信息的优化方案和SPRT方案、SPOT方案,从图4、图5来看,不融合先验信息的优化方案不一定具备比SPRT方案和SPOT方案更少的平均样本量,但是具备更小的后验概率,能基于后验概率以及“小概率事件原理”进行决策,同时融合先验信息能很大程度上减少平均样本量和平均检测失败次数,当FDR指标值越高,同时融合专家信息和成败型信息的优化DS-SPOT方案具备比SPRT方案、SPOT方案更小的平均样本量。 6) 分析3种不同融合方式的曲线,能反映出先验信息对于决策H0的支持度越高,则所需平均样本量和平均检测失败数越小。由此可见,优化DS-SPOT方案所需平均样本量与先验信息对于决策Hi的支持程度有关,如果先验信息支持作出决策Hi,则所属决策域所需平均样本量相对会减少,能帮助测试性验证试验更快的进行决策判断,缩短验证周期以及控制验证成本。 基于对SPOT测试性验证方案中模糊参数空间的考虑不足以及未能充分利用研制阶段多源先验信息的问题,本文提出了一种基于优化DS-SPOT的测试性验证方案,具备以下优点: 1) 考虑了假设检验问题中的模糊参数空间,不再是简单的接收/拒收判决,决策给出测试性指标实际所在的参数空间,为承制方和使用方提供更合理的参考依据;考虑了研制阶段的多源先验信息,通过证据理论对其进行融合,使得装备研制阶段存在的测试性研制信息得到合理的运用。 2) 与固定抽样方案相比,融合先验信息的优化DS-SPOT方案能根据实际序贯过程进行判决,且具备比固定抽样方案小的平均样本量;与序贯类测试性验证方案相比,能充分融合多源信息,在先验信息支持决策的参数空间内具备比SPRT、SPOT方案相对较小的平均样本量。 3) 随着先验信息对所支持决策的参数空间的支持度提高,相应的平均样本量相应减小。 可见,本文所提方案能充分融合多源先验信息以及考虑承制方和使用方测试性指标间的模糊参数空间,一方面能有效减少验证试验所需样本量,另一方面能为承制方和使用方提供更加科学、合理的决策结果。 但是,除了文中进行讨论的研究点外,仍有一些问题需要进行进一步的研究: 1) 由于序贯试验的随机性,序贯方案的最大样本量可能无法有效控制,本文给出的固定截尾方案是一种有效形式,但同时也会造成决策风险,下一步应当在控制风险的前提下研究更为合理有效的截尾措施。 2) 先验信息的运用是优化DS-SPOT方案的关键一环,准确的先验信息有助于提高决策判定的可信度,现有文献对先验信息可信度的研究比较多,但不够系统。因此有必要开展先验信息纳入体系的研究,以保证先验信息来源和使用的合理性、准确性和便捷性。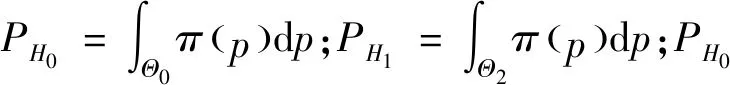
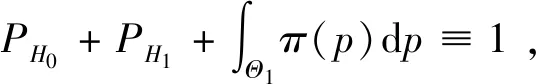
2 优化SPOT序贯试验方案设计
2.1 三参数空间的序贯后验概率
2.2 三参数空间的Bayes序贯检验决策规则
3 D-S证据理论融合多源先验信息
3.1 成败型试验信息的基本信任分配函数
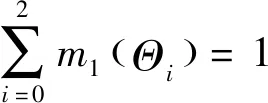
3.2 专家信息的基本信任分配函数
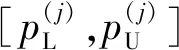
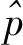
3.3 优化序贯验证方案确定
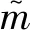
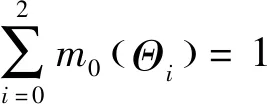
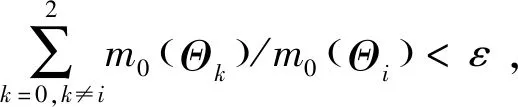
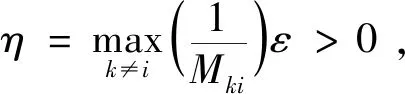
4 案例分析
4.1 先验信息确定

4.2 测试性验证方案对比分析
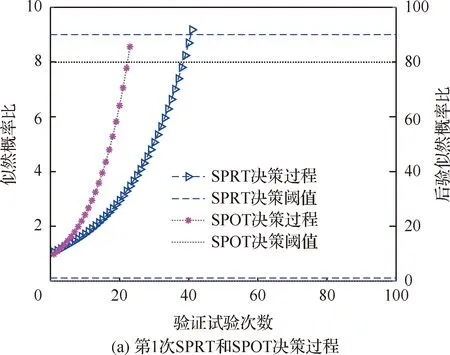
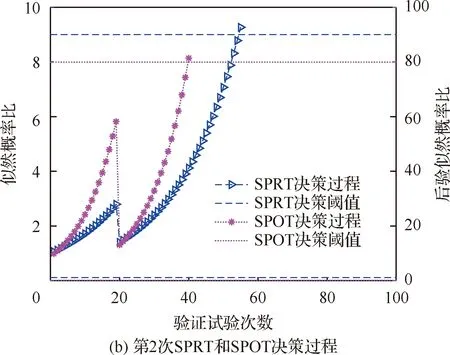
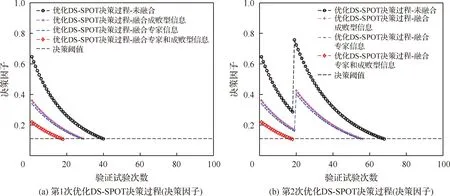
Table 2 Results of different sequential programs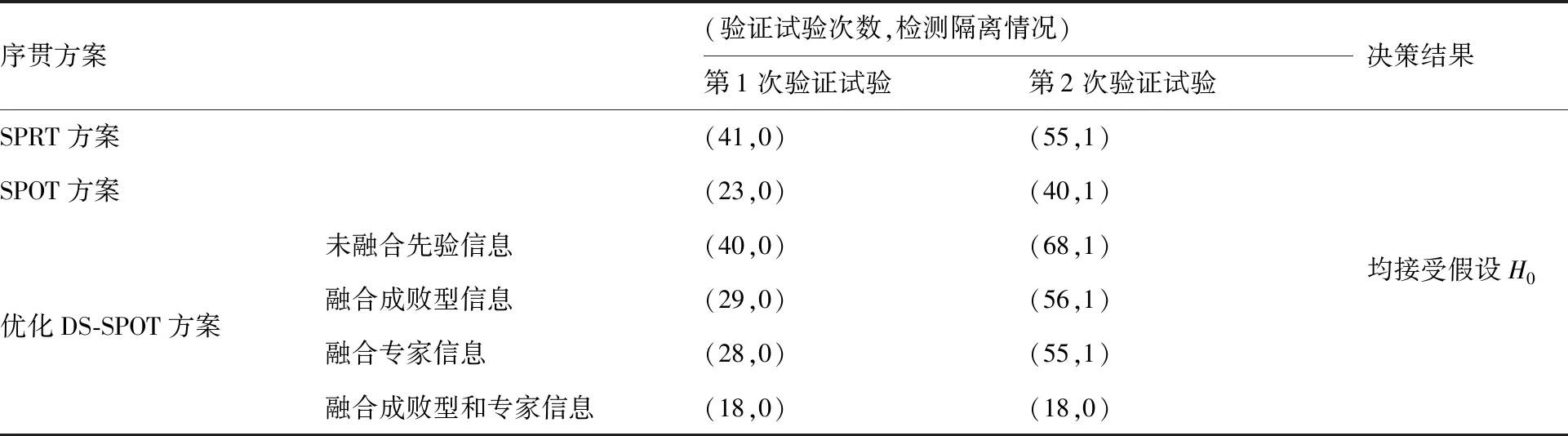
4.3 平均样本量
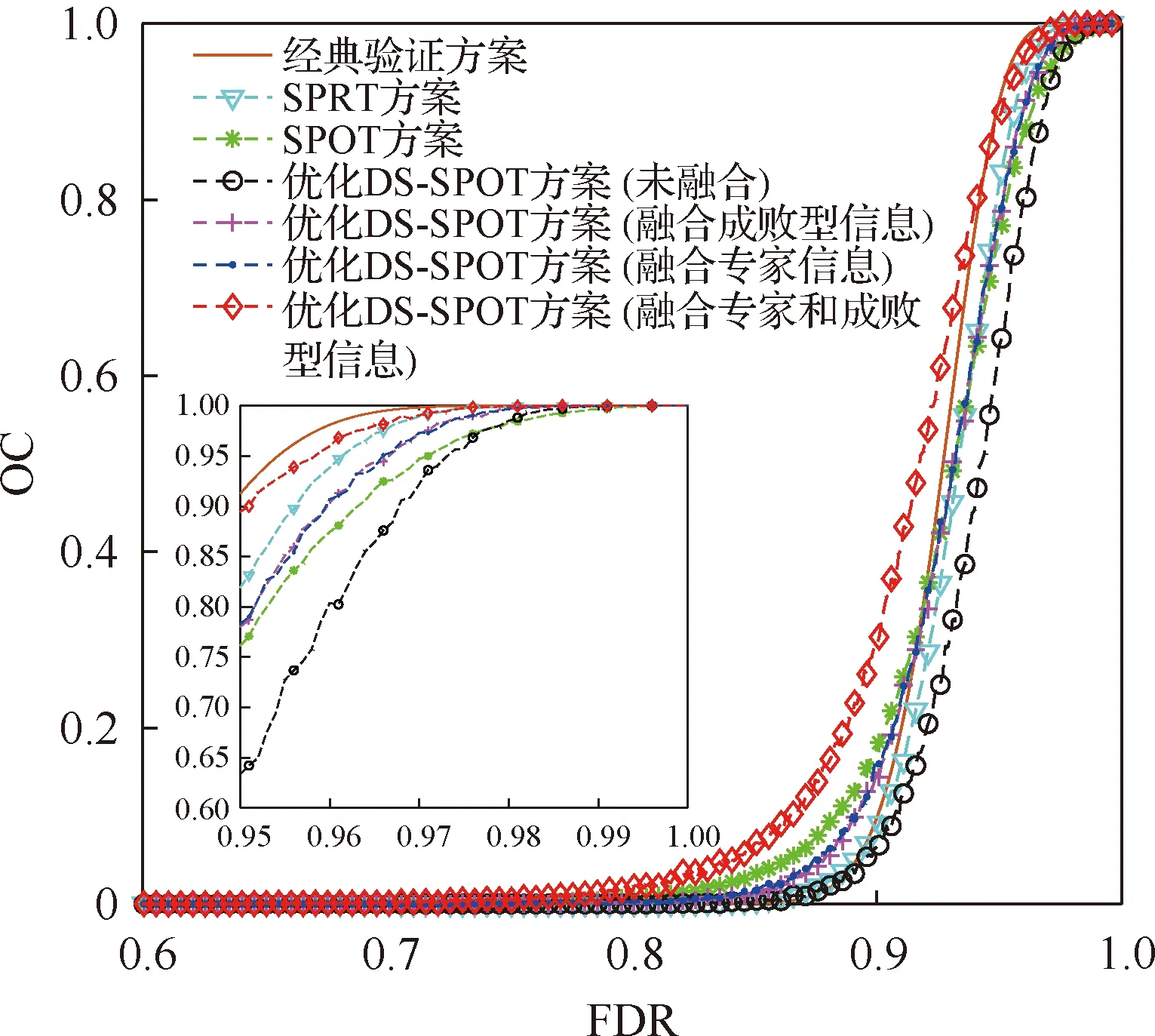
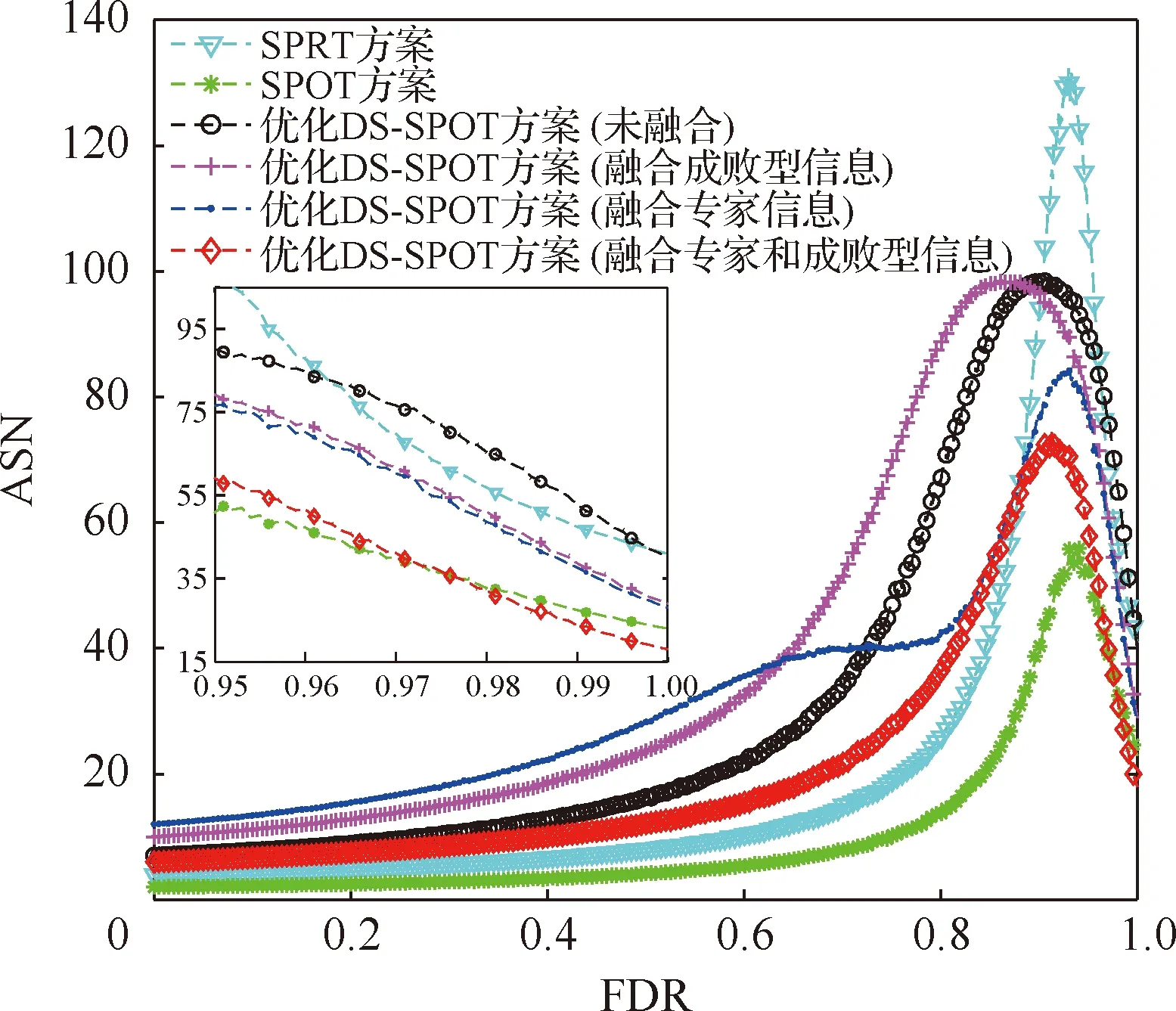
5 结 论
