升力偏置对共轴刚性旋翼前飞气动特性的影响
2019-12-09卢丛玲祁浩天徐国华
卢丛玲,祁浩天,徐国华
南京航空航天大学 直升机旋翼动力学国家级重点实验室,南京 210016
传统单旋翼构型的直升机由于受到前行桨叶激波和后行桨叶失速的限制,无法高速前飞。共轴直升机具有结构紧凑、操纵性好等特点,同时能够达到较高的飞行速度,在军民领域都有广泛应用。西科斯基公司将前行桨叶概念(Advancing Blade Concept, ABC)[1]应用于共轴旋翼复合式直升机,研制了X2技术验证机,其巡航速度可达463 km/h[2]。共轴刚性旋翼复合式直升机正成为高速直升机研究的热点。前行桨叶概念旋翼在高速前飞时,能够充分利用前行侧桨叶动压大的特点,使旋翼升力偏向前行侧,后行侧桨叶则产生较小升力,以改善旋翼气动性能。这样就会使旋翼升力偏离旋翼轴,而共轴双旋翼旋转方向相反,产生的滚转力矩可以相互平衡。旋翼总升力偏离旋翼轴的横向距离与半径的比即为升力偏置量(Lift Offset, LOS)。升力偏置是共轴刚性旋翼一种特殊的气动特征。升力偏置量的大小对共轴刚性旋翼的气动性能和非定常载荷特性有重要影响,因此针对共轴刚性旋翼的升力偏置状态展开研究是十分必要的。
目前,国内外很多学者开展了关于共轴旋翼气动特性的研究。为了研究升力偏置对共轴刚性旋翼的影响,Johnson[3]提出了适用于共轴旋翼的动量理论;Bagai[2]建立了基于升力线理论的广义旋翼性能分析方法。涡方法[4-8]也常被用于分析共轴旋翼的气动性能和尾迹特征。其中Schmaus和Chopra[4-5]基于马里兰大学的旋翼分析程序,建立了适用于共轴旋翼的自由尾迹方法以研究升力偏置量对其气动性能的影响。Yeo 和Johnson[9]采用基于升力线理论和尾迹方法的旋翼气动分析模型(CAMRAD II),计算了升力偏置量对旋翼升力、扭矩和操纵及桨叶载荷的影响。谭剑锋等[10]结合面元法和黏性涡粒子方法分析了X2旋翼的非定常载荷,发现高速前飞时双旋翼载荷受桨叶干扰明显,非定常载荷波动频率与桨叶片数对应。动量理论和尾迹方法对研究共轴刚性旋翼的气动干扰特征有重要意义。相比之下,计算流体力学(CFD)方法在捕捉双旋翼流场干扰细节和非定常载荷计算方面也有着不可替代的优势[11]。Lakshminarayan和Baeder[12]采用雷诺平均Navier-Stokes (RANS)方程求解器和滑移网格计算了悬停状态共轴旋翼的非定常干扰特性;针对其周期性旋翼载荷波动特点,提出了“厚度效应”和“ 载荷效应”两种解释。朱正等[13]采用运动嵌套网格方法揭示了共轴旋翼悬停状态下的尾迹特征和干扰机理。Barbely等[14-15]采用旋翼非结构Navier-Stokes方程求解器,计算了共轴旋翼悬停和前飞状态的干扰流场。Klimchenko等[16]将CFD与计算固体力学(CSD)方法耦合,分析了前飞状态下的共轴旋翼气动和结构载荷特征。这些研究多着重于共轴刚性旋翼气动干扰特性方面,但关于共轴刚性旋翼前飞,尤其是大前进比状态下,升力偏置对其气动性能影响的研究却较少。
鉴于此,本文在课题组建立的旋翼流场计算方法[17-18]基础上,通过求解RANS方程和应用运动嵌套网格方法,计算共轴刚性旋翼在不同前进比和升力偏置量状态下的气动性能和流场特性。升力偏置是共轴刚性旋翼的重要特征,对共轴刚性旋翼气动特性有很大影响,所以针对不同升力偏置状态对其进行操纵量配平是十分必要的。首先,本文采用基于“差量法”的共轴刚性旋翼高效配平方法[19]进行操纵量配平,以保证升力偏置状态模拟的准确性。然后,通过分析不同升力偏置量状态下共轴刚性旋翼的操纵量、气动载荷和流场特征,着重研究大前进比下,升力偏置对共轴刚性旋翼升阻比、扭矩和阻力等气动性能的影响机理及共轴刚性旋翼的气动干扰特征。
1 数值计算方法
1.1 共轴刚性旋翼流场模拟方法
采用雷诺平均Navier-Stokes方程进行流场求解,其积分形式的表达式为
(1)
式中:S、V分别为控制体表面积和体积;W为守恒变量;Fc和Fv分别为对流通量和黏性通量,其表达式分别为
(2)

计算中采用双时间步方法以求解旋翼非定常流场,空间离散采用Roe[20]格式,采用Spalart-Allmaras湍流模型[21]求解黏性项,采用运动嵌套网格系统以模拟双旋翼运动。其中,桨叶网格采用C-O型贴体网格,背景网格为笛卡儿网格。对背景网格在桨盘区域和旋翼尾迹区域进行加密。计算中采用的运动嵌套网格系统如图1所示。
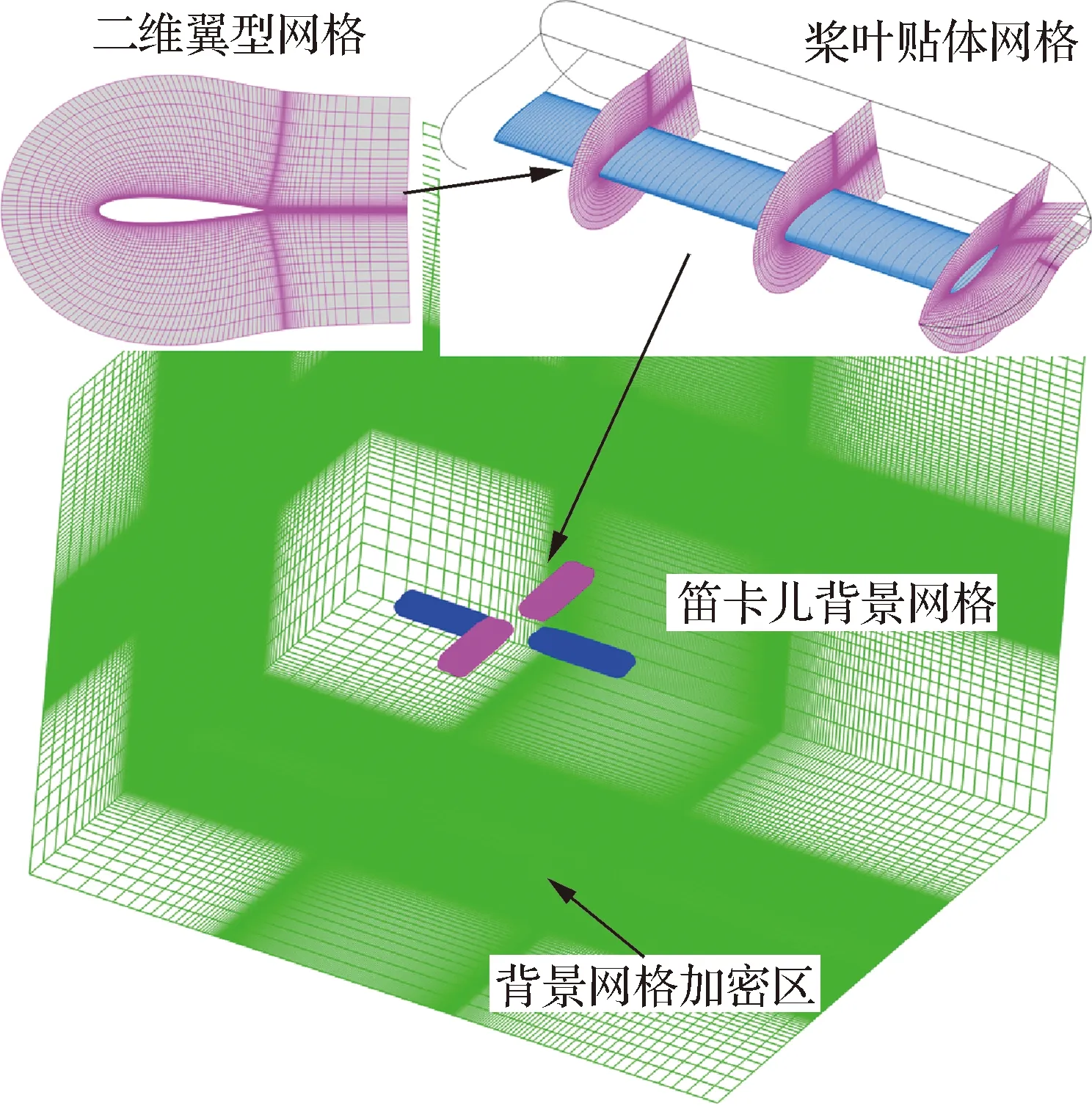
图1 共轴旋翼运动嵌套网格系统示意图Fig.1 Illustration of overset grid system for coaxial rotor
1.2 共轴刚性旋翼配平策略
本文采用基于差量法的共轴刚性旋翼高效配平策略[19],对该共轴刚性旋翼模型的前飞状态进行配平。差量法配平的核心是用高效的简单气动模型代替CFD方法求解雅克比矩阵,以提高计算效率。同时,使用CFD方法对简单模型计算的气动力结果进行纠正,以保证配平精度。
配平操纵量为
(3)
式中:θ0为旋翼总距;θ1s为横向周期变距;θ1c为纵向周期变距;上标u表示上旋翼,l表示下旋翼。
配平目标量为
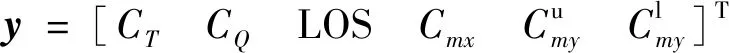
(4)
式中:CT为总拉力系数;CQ为总扭矩系数;Cmx为滚转力矩系数;Cmy为俯仰力矩系数。共轴刚性旋翼的升力偏置量可表示为
(5)
由于在扭矩平衡状态,双旋翼拉力可能不同,因此本文采用共轴旋翼平均升力偏置量[22],而不是单独上(下)旋翼的升力偏置量,见图2。其中,由于双旋翼滚转力矩的正方向相反,因此式(5)中分子项中双旋翼滚转力矩是相减的。

图2 共轴刚性旋翼升力偏置示意图[22]Fig.2 Illustration of lift offset of rigid coaxial rotor[22]
1.3 计算方法验证
图3和图4对比了本文计算的Harrington-1旋翼[23-24]气动性能和试验结果,其中,ΩR为旋翼桨尖速度,μ为前进比。在悬停状态下,给定一系列拉力系数,使用本文的配平方法得到扭矩平衡状态下的总距,根据总距计算旋翼性能,再对结果进行比较。前飞计算时目标拉力系数为0.004 8,其余5个目标量均为零,旋翼轴倾角采用文献[14]中所给出的值。可见,单旋翼计算结果与试验值吻合良好。相比之下,双旋翼计算结果与试验值有一定误差。这一方面是由于双旋翼配平的操纵量与真实操纵量可能有一定偏差,另一方面与双旋翼间的复杂气动干扰有关。总体来看计算误差在合理范围内,所建立的数值模拟方法是可靠的。
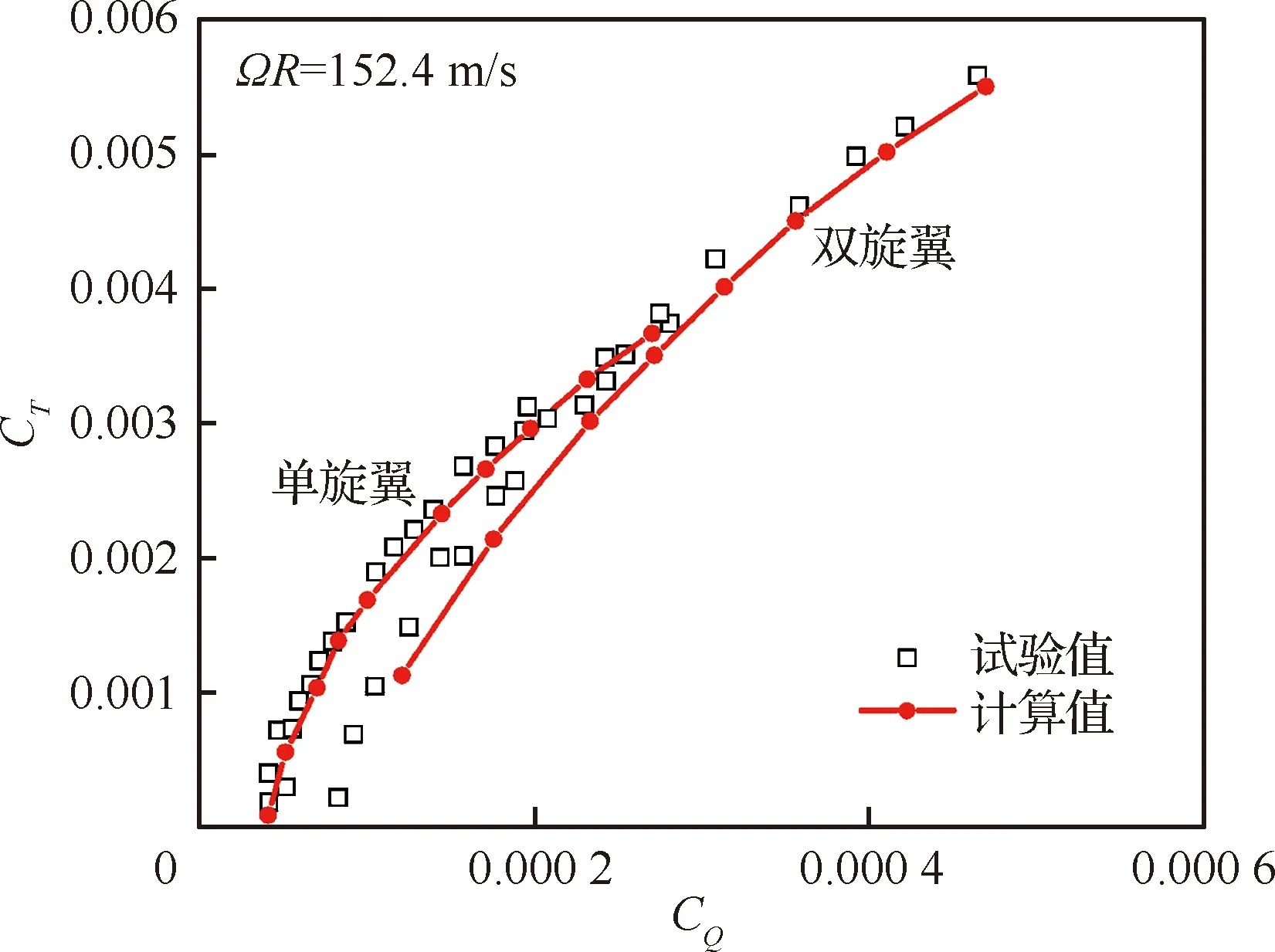
图3 Harrington-1旋翼悬停性能对比Fig.3 Comparison of hover performance of Harrington-1 rotor
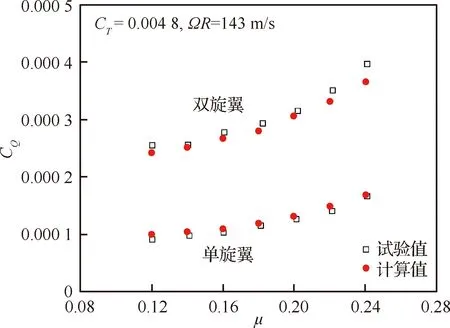
图4 Harrington-1旋翼前飞性能对比Fig.4 Comparison of forward flight performance of Harrington-1 rotor
2 配平结果与分析
本文所采用的共轴刚性旋翼模型参数如表1所示。该模型旋翼半径R为2 m,桨叶弦长c为0.22 m,每副旋翼有两片桨叶,展弦比约为9.1。桨叶无扭转、定弦长,采用NACA0012翼型。在前进比小于0.4时桨尖马赫数为0.587,当前进比大于或等于0.4时桨尖马赫数下降至0.47,以避免大前进比状态前行侧桨尖处马赫数高于0.9[11]。计算中采用的笛卡儿背景网格节点数为245×210×218,分别对应x、y、z方向;每片桨叶网格节点数为221×87×101,分别对应桨叶周向、法向和展向;总网格量约1 900万。计算中对靠近旋翼桨尖区域的桨叶网格和背景网格进行了加密,加密后的网格尺寸约为0.05c。
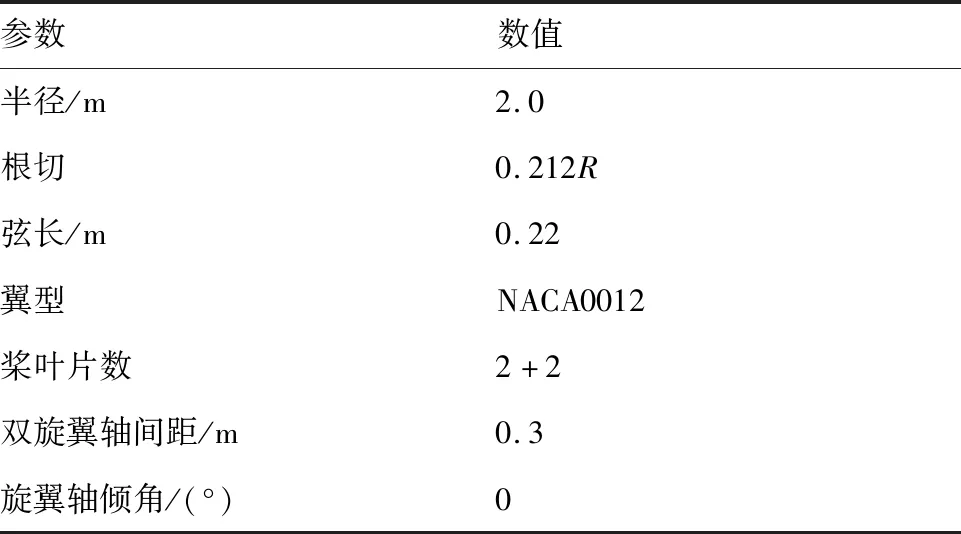
表1 共轴刚性旋翼模型参数Table 1 Rigid coaxial rotor model parameters
配平时共轴模型旋翼目标拉力系数为0.001,作为对比计算的单旋翼采用与上旋翼相同的操纵量。图5和图6给出了不同前进比和升力偏置状态下,共轴旋翼操纵量配平结果。可见,在前进比为0.1时,双旋翼操纵量有明显差别,且这种差别随升力偏置量的增大而变大。其中,双旋翼纵向周期变距之差大于总距差。这主要是由于,在这种小前进比状态双旋翼尾迹仍然有较强的干扰,且这种干扰使双旋翼桨盘前后流场不对称性增强;在保持俯仰力矩平衡的条件下,双旋翼纵向周期变距差增大。随着前进比增大,双旋翼间干扰减弱,双旋翼操纵量逐渐趋于一致。在前进比为0.5时,双旋翼操纵量差值很小,基本一致。同时可以发现,随着升力偏置量的增大,旋翼总距和纵向周期变距都减小,其中总距减小幅值明显较大;而横向周期变距则由负值逐渐增大变为正值。
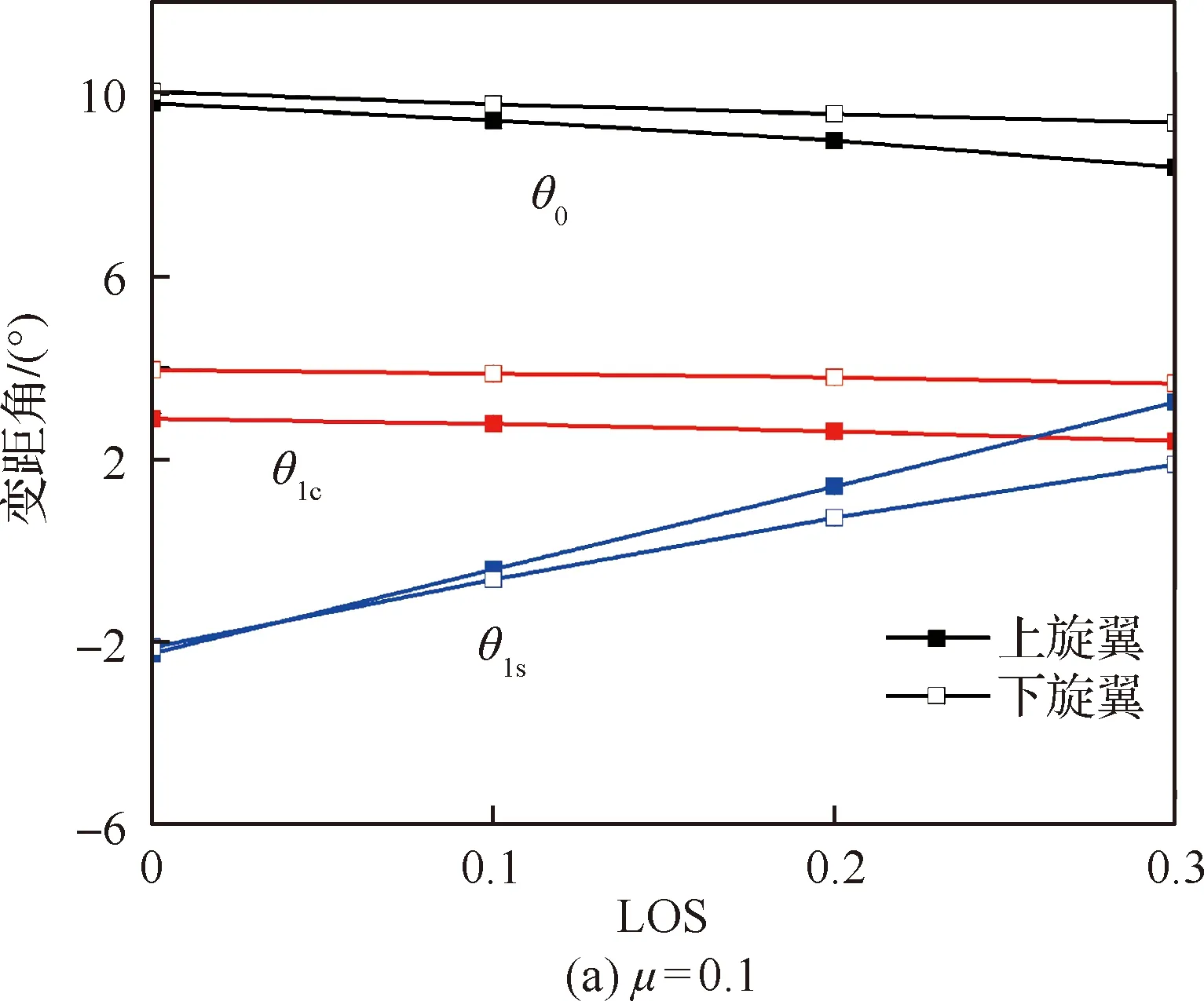
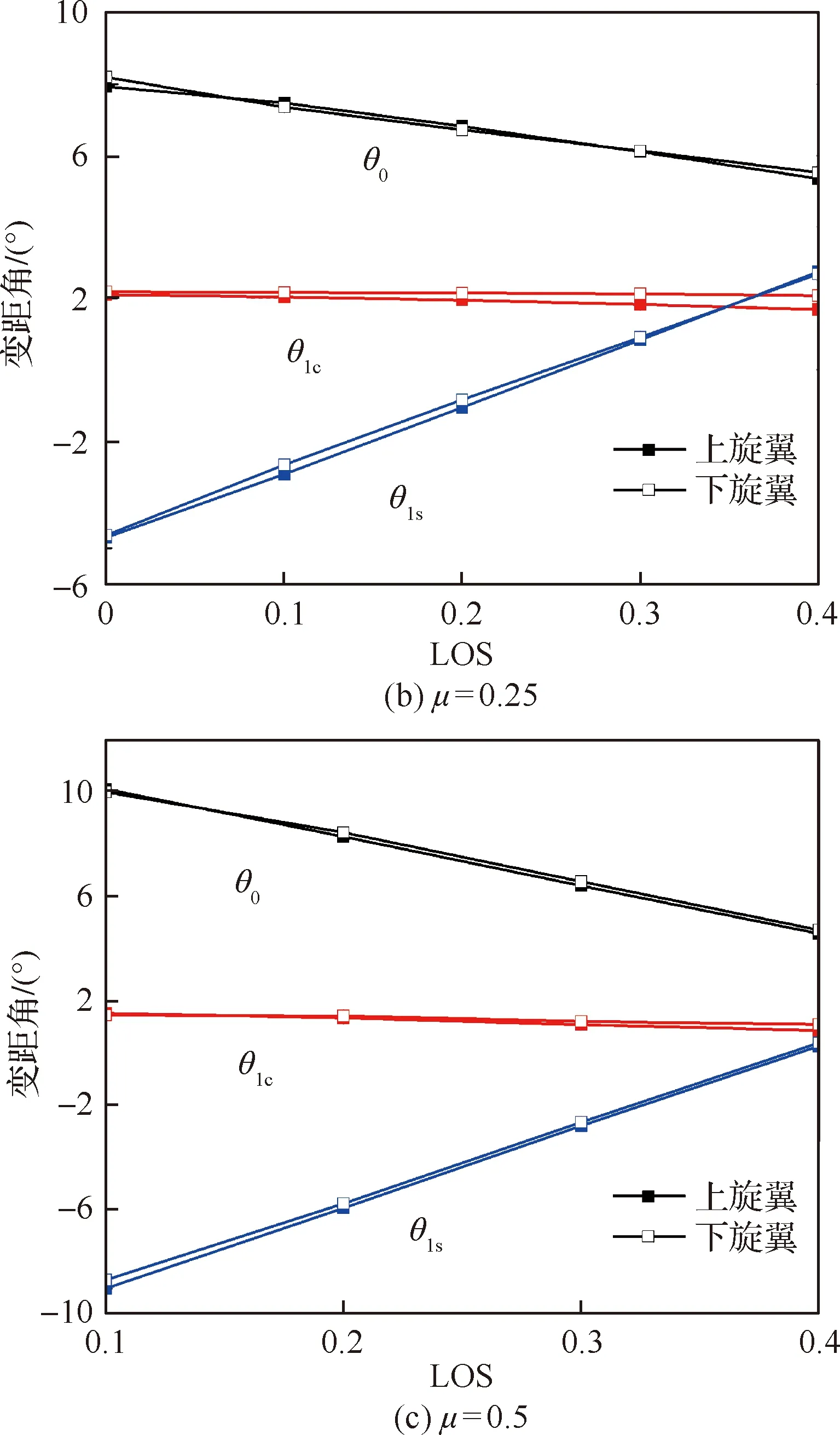
图5 不同LOS状态共轴旋翼配平操纵量Fig.5 Trimmed pitches of coaxial rotor for different LOS
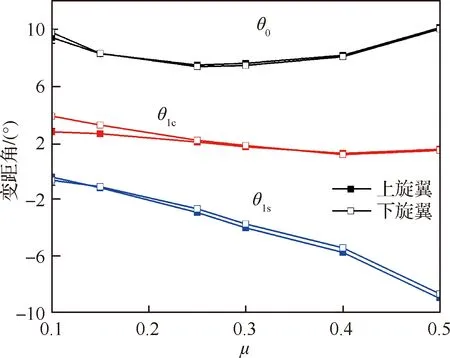
图6 不同前进比共轴旋翼配平操纵量(LOS=0.1)Fig.6 Trimmed pitches of coaxial rotor for different advance ratios (LOS=0.1)
图6给出了保持LOS=0.1,不同前进比状态下的共轴旋翼配平操纵量配平结果。可见,随着前进比增大双旋翼总距先减小后增大,横向周期变距逐渐减小但变化幅值较小,纵向周期变距的减小速度明显增大。
3 升力偏置对气动特性的影响
3.1 旋翼气动性能分析
旋翼前飞升阻比(L/D)定义[2]为
(6)
式中:L为升力;D为阻力;CL为风轴系下旋翼升力系数;CD为风轴系下旋翼阻力系数。可见,等效阻力由旋翼阻力(CD)和功率当量阻力(CQ/μ)两部分组成。
图7给出了升力偏置量对共轴旋翼升阻力特性的影响。可见,随着升力偏置量增大,旋翼升阻比先增后减小。不同前进比状态,最大升阻比对应的升力偏置量不同。μ=0.25时,升阻比在LOS=0.1达到最大。μ=0.4和μ=0.5时,升阻比均在LOS=0.2达到最大值。
由图7(b)可见,μ=0.25时,双旋翼扭矩在LOS=0.2最小;前进比为0.4时扭矩最小值在LOS=0.3处。μ=0.5时扭矩随升力偏置量增大而下降,在LOS=0.4时这种下降幅度明显减小。可见,适当的升力偏置量能够降低共轴旋翼扭矩;前进比越大,最低扭矩点对应的升力偏置量也越大。由图7(c)可见,随着升力偏置量的增加,旋翼阻力随之增大。这是由于升力偏置量增大使桨叶瞬时阻力在桨盘内的分布随之偏移,使旋翼桨盘内的合阻力增大。
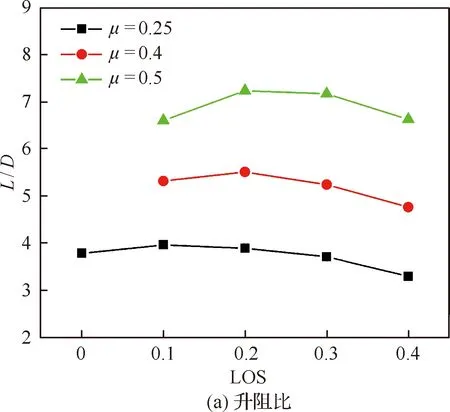
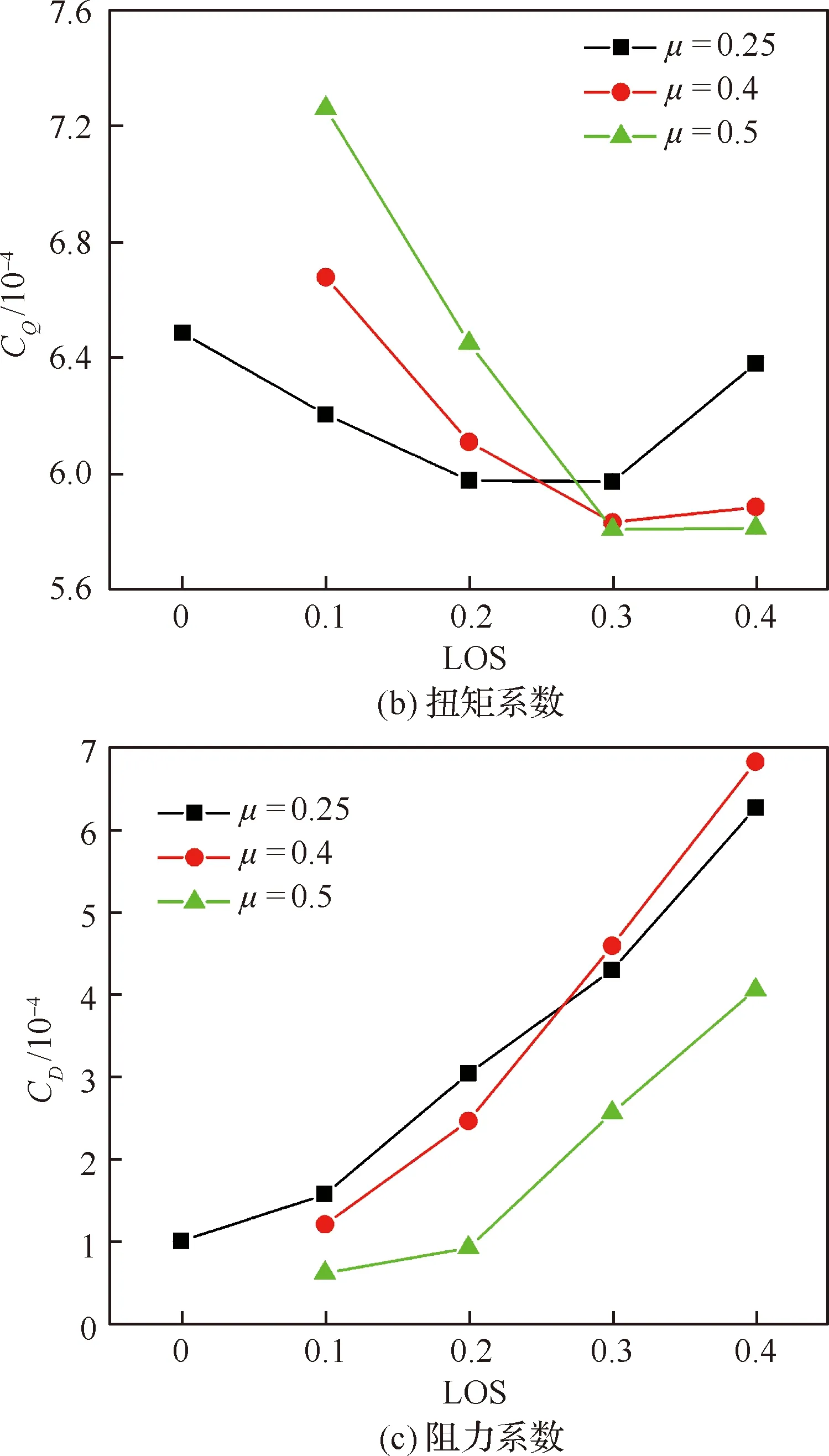
图7 不同升力偏置量共轴刚性旋翼性能对比Fig.7 Comparison of rigid coaxial rotor performance for different LOS
3.2 桨叶瞬时载荷分析
图8给出了不同升力偏置量下的共轴旋翼和单旋翼单片桨叶的瞬时拉力系数变化。可见,升力偏置增大后前行侧桨叶拉力明显大于后行侧。μ=0.25时双旋翼与单旋翼仍有明显差别,这是由于在该前进比状态双旋翼尾迹仍然有相互干扰。前进比为0.5时,共轴旋翼气动干扰减弱,双旋翼和单旋翼的桨叶瞬时拉力也趋于一致;且随着升力偏置量的增大,双旋翼与单旋翼桨叶瞬时拉力差也随之减小。
同时可以发现,与悬停状态下双旋翼相遇时由 “厚度效应”[12]所引起的拉力波动类似,双旋翼桨叶拉力在每个相遇方位角附近(每隔90°)仍然有相反的脉冲式拉力波动。这种双旋翼相遇引起的脉冲式拉力波动在前行侧(90°方位角)处最不明显,在270°方位角处最显著,表现为上桨叶拉力突降下桨叶拉力突增,但上桨叶拉力下降幅值明显大于下桨叶增加幅值。可见,这种桨叶相遇时的干扰,在上旋翼后行侧的桨叶拉力上表现得较为明显。
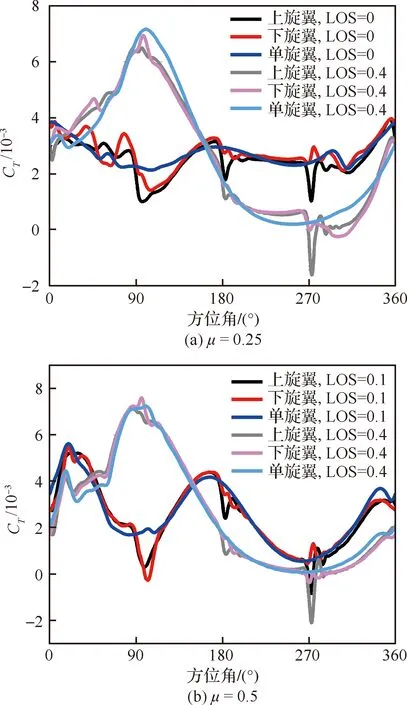
图8 桨叶瞬时拉力系数变化Fig.8 Temporal variations of blade CT
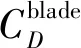
1) 在后行侧270°方位角附近桨叶阻力与图8中的桨叶拉力相似有明显的脉冲性波动,不同之处在于,上桨叶拉力波动明显大于下桨叶,而上、下桨叶的阻力波动幅值则相差不大;且上、下桨叶阻力均以脉冲的形式突然增大。
2) 在桨叶阻力沿方位角的分布方面,双旋翼与单旋翼均随着升力偏置的增大而逐渐向前行侧(90°方位角)偏移。旋翼合阻力方向沿着图中0°~180°方位角轴线,因此这种桨叶瞬时阻力分布的偏移会导致旋翼整体阻力增大。
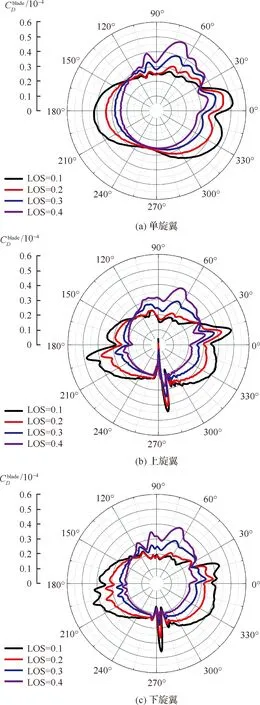
图9 桨叶瞬时阻力系数变化(μ=0.5)Fig.9 Temporal variations of
图10给出了μ=0.5时,不同升力偏置量状态下的旋翼纵向剖面压力系数Cp分布。从单旋翼截面压强分布可见,位于前行侧(90°方位角)的桨叶动压较大,引起较大范围的压强变化;位于后行侧(270°方位角)的桨叶动压较小,产生的压强变化范围也较小。对比两种升力偏置量的单旋翼截面压强分布,可见,由于LOS=0.1时前行侧桨叶迎角较小,桨叶上方和下方都有明显的负压区;而LOS=0.4时前行侧桨叶迎角较大,桨叶上方为负压区,下方为正压区,且上方的负压区的范围明显大于下方的正压区,因此下旋翼对上旋翼的干扰更加明显。从双旋翼截面压强可见,由于双旋翼反转,上旋翼前行侧(后行侧)与下旋翼后行侧(前行侧)桨叶产生干扰,流场被前行侧桨叶主导,且随着升力偏置量的增大,前行侧桨叶对流场的主导效果也随之增强。这与前文图8(b)中,270°方位角附近旋翼拉力的脉冲波动相对应。
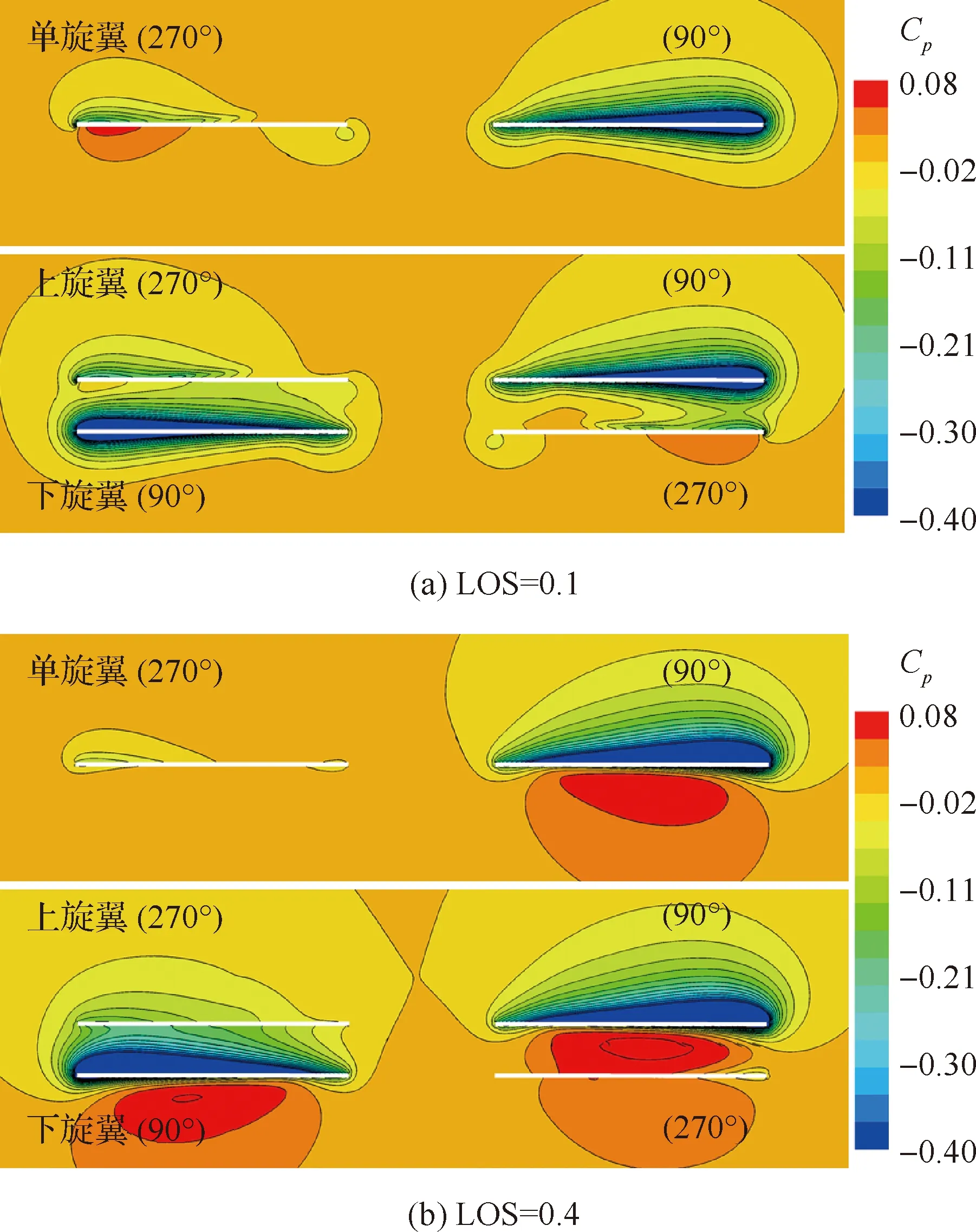
图10 旋翼展向截面压力系数分布(μ=0.5)Fig.10 Cp contours in span cross-sections of rotor (μ=0.5)
图11给出了两种前进比状态下的共轴旋翼纵向剖面涡量云图。可见,随着前进比的增大,双旋翼尾迹迅速向后发展,桨盘附近双旋翼尾迹间的干扰减弱。这与图8中双旋翼与单旋翼桨叶瞬时拉力基本一致的现象对应。
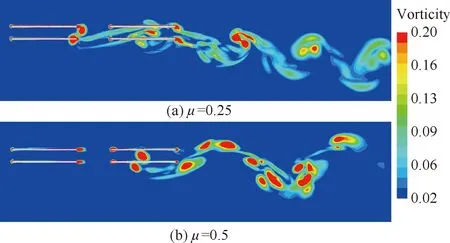
图11 共轴旋翼纵向剖面涡量云图Fig.11 Vorticity magnitude contours in longitudinal sections for coaxial rotor
4 结 论
本文基于CFD方法和运动嵌套网格技术,采用适用于共轴刚性旋翼的高效配平方法进行操纵量配平,以模拟其升力偏置特征。通过对共轴刚性旋翼前飞时不同升力偏置状态下的操纵量、气动性能和流场分析,得到如下结论:
1) 共轴双旋翼总距随着升力偏置量的增大而减小;而横向周期变距则由负值逐渐增大变为正值。在小前进比时双旋翼尾迹有较强干扰,双旋翼操纵量有明显差别。干扰引起桨盘流场前后不对称性增强,双旋翼横向周期变距差值也随之增大。在大前进比时双旋翼干扰减弱,操纵量也基本一致。
2) 随着升力偏置量增大,共轴旋翼升阻比先升高后降低,但阻力随之增加。这是由于一方面升力偏置充分利用前行侧桨叶动压大、气动效率高的特点改善了旋翼气动性能,另一方面升力偏置使桨盘阻力分布偏向前行侧而使整体阻力增大。不同前进比状态,最大升阻比对应的升力偏置量不同。
3) 双旋翼相遇时的上、下旋翼的桨叶拉力出现脉冲式波动。由于桨叶相遇时流场被动压大的桨叶所主导,且上旋翼受到下旋翼的干扰更大,因此这种拉力脉冲波动在上旋翼后行侧(270°附近)的桨叶上表现得更为明显。升力偏置量越大,这种干扰引起的拉力脉冲波动幅值也越大。
4) 前飞状态双旋翼尾迹在桨盘附近的干扰随前进比的增大而逐渐减弱。在前进比为0.5时,除270°附近的脉冲波动外,共轴旋翼的桨叶瞬时拉力与单旋翼的桨叶瞬时拉力基本一致;且双旋翼与单旋翼桨叶瞬时拉力差随着升力偏置量的增大而有所减小。
