一种准确预测层合梁结构层间剪应力的新锯齿理论
2019-12-09杨胜奇张永存刘书田
杨胜奇,张永存,刘书田
大连理工大学 工程力学系 工业装备结构分析国家重点实验室,大连 116024
层合结构是由不同材料属性的薄片通过某种工艺(如粘接)复合而成。现有的层合结构包括纤维增强复合材料[1-2]、三明治夹层结构[3-4]和钛合金层合结构[5]等多种形式,具有参数可设计性强、性价比优等特点,被广泛应用于航空航天领域[6-7]。在层合结构中,通常不同材料之间连接界面的力学性能最为薄弱。过大的层间应力会导致层合结构损伤破坏,成为其失效的主要形式[8-9]。如纤维增强复合材料损伤失效有50%以上是分层引起的[10]。因此,准确预测层合结构的层间应力尤为重要。
层合梁是航空航天领域典型的承力构件,已经发展了多种分析模型,用于计算其横向剪应力,从而获得层间应力。现有的分析模型主要分为3类:等效单层理论[11-12]、分层理论[13-14]和锯齿理论[15-18]。等效单层理论的计算效率较高,然而由于无法满足层间剪应力连续条件,计算误差较大。如Timoshenko梁理论预测的三明治夹层梁的横向剪应力,计算误差高达351%[18]。理论上,分层理论能够准确预测复合材料层合结构的层间剪应力,但所需的计算量十分庞大。如300层的层合板,每个节点自由度数高达1 803个[19]。锯齿理论是在整体高阶理论的基础上添加合适的局部锯齿函数构造而成的。通常整体理论不超过三阶,而锯齿函数能够描述面内位移沿厚度方向的锯齿[20]变化。显然,如果选择合适的锯齿函数,锯齿理论只需较少的未知变量就能够准确计算层合结构的横向剪应力,从而很好地兼顾计算效率和计算精度,成为当前研究的主要方向。
锯齿理论最早由Lekhnitskii[21]于1935年提出,提出后并未引起重视,直到1986年Murakami锯齿理论[15]和Di Sciuva锯齿理论[22]的提出,锯齿理论才逐渐被认可。由于Di Sciuva锯齿理论能够预先满足层间应力连续条件,得到快速发展。基于Di Sciuva锯齿理论,Cho和Oh[23]提出了一种三阶锯齿模型,并将之用于预测承受力、热和电载荷的复合材料厚板的变形和应力。早期的锯齿理论[15-17,22-23]仅适用于预测层数较少的层合梁和材料属性差异不大的三明治夹层梁的横向剪应力。2015年,Tessler等[18]基于经典的修正锯齿理论(RZT),提出了一种混合修正锯齿理论(RZTM)[24-25]。贺丹和杨万里[26]应用该理论分析了层合梁的弯曲和自由振动问题。该理论能够准确计算出材料属性差异较大的夹层梁的横向剪应力。然而对于层数较多的层合梁,预测精度较差。常见的T300/QY8911复合材料的单层厚度为0.12 mm[27],在实际的航空结构中,超过25层的纤维增强复合材料(即厚度超过3 mm)十分常见,如机翼蒙皮[28]。因此,发展能够准确预测较多层数的层合结构横向剪应力的锯齿理论是非常必要的。基于整体高阶锯齿理论[29],Wu和Chen[30]提出了一种混合整体高阶锯齿理论(GHZTM),能够准确预测大多数的多层厚梁的横向剪应力,然而个别多层梁横向剪应力预测精度稍差(如3层层合梁[30])。另外,该理论的挠度场要求满足C1连续,为C1型锯齿理论,不利于梁单元的构造。早期的锯齿理论大都是C1型锯齿理论。2011年,Ren等[31]提出了一种C0型锯齿理论的构造方法,并提出了一种C0板单元。由于C0型锯齿理论具有计算效率高,容易在商业软件实现等优点,而得到快速发展。随后,许多C0型锯齿理论[32-34]和C0单元[35-38]被提出。Wu等[39]比较了大量的C0和C1型锯齿理论模型,发现相比于C1型锯齿理论C0型锯齿理论不仅有更高的计算效率还具有更高的计算精度。
本文提出了一个新的线性分段锯齿函数,采用Ren等[31]提出的C0型锯齿理论构造方法,建立了一种面向层合梁结构的C0型新锯齿理论模型。该模型不仅能够准确预测层数较多的纤维增强复合材料层合梁的横向剪应力,同时能够准确预测芯层与上下面板材料属性差异较大的三明治夹层梁的横向剪应力。
1 锯齿理论描述
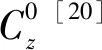
锯齿层合梁理论的位移场可统一表示为
(1)
式中:z为厚度坐标;k表示第k层;u0和w0为中面位移;u1为中面法线方向绕y轴的转角,ui为泰勒级数展开的高阶项;j表示整体部分的阶次,如j=1表示整体一阶,j=3表示整体三阶;uz(x)为锯齿函数。
MZZT锯齿理论[15]的锯齿函数可写为
uz(x,z)=(-1)kζkψ(x)
(2)
式中:ζk为每层z方向的局部坐标,ζk=akz-bk,ζk∈(-1,1),ak=2/(zk+1-zk),bk=(zk+1+zk)/(zk+1-zk);ψ(x)为锯齿转角,度量锯齿函数对沿厚度分布的轴向位移的影响程度。对于任意x=xa,MZZT锯齿函数沿厚度的变化如图1所示[15]。从图1和式(2)可知,MZZT锯齿函数在层和层交界面处的值,只能从-ψ(xa)和ψ(xa)中选取。此外,该锯齿函数不依赖于每层材料的性质,无法描述每层材料属性的变化,导致该理论无法准确预测横向各向异性的层合梁的变形和应力[40]。尤其对于面板软夹层硬的夹层结构,其预测精度较差[41]。
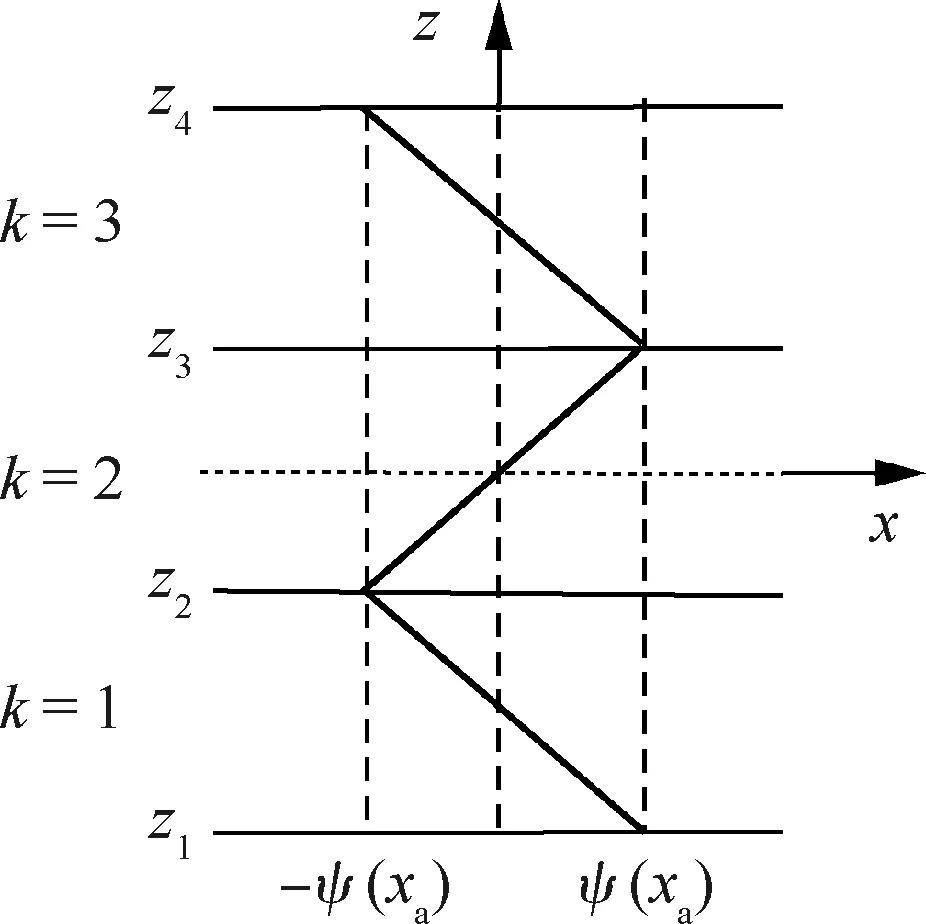
图1 MZZT锯齿函数[15](三层梁)Fig.1 MZZT zig-zag function[15](for a three-layer beam)
RZT锯齿理论[18]的锯齿函数可写为
(3)
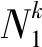
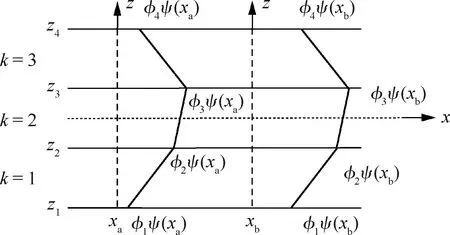
图2 不同梁截面处RZT锯齿函数[18](3层梁)Fig.2 RZT zig-zag function at different beam sections[18](for a three-layer beam)
2 新锯齿理论模型
2.1 新锯齿函数
新锯齿函数为
(4)
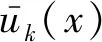
2.2 位移场
位移场的整体部分仍取三阶,因此,构造的初始位移场为
(5)
式(5)中共含有n+6(n为层数)个未知变量,并且未知量个数与层数相关。下面推导的目的是消去部分未知量,得到最终位移场。
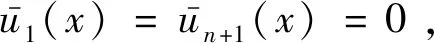
其次,使用横向剪应力层间连续条件
(6)
和横向剪应力自由表面条件
(7)
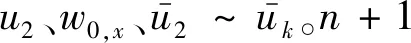
Ku=Au1+Bu3
(8)
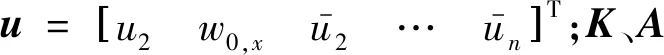
u=K-1Au1+K-1Bu3
(9)
式(9)可重写为
u=C1u1+C3u3
(10)
式中:C1=K-1A,C3=K-1B。
将式(10)代入式(5)中,高阶锯齿理论最终位移场可写为
(11)
当k=1时:
当k=2~n-1时:
当k=n时:
该理论仅含有4个与层数无关的未知量。不含有横向位移的一阶导数,构造有限单元时,仅需满足C0连续。
2.3 几何方程和本构方程
对于线弹性问题,层合梁的几何方程为
(12)
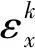
第k层层合梁的本构方程为
(13)
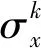
2.4 横向剪应力的预处理
为了获得更为精确的横向剪应力,Tessler[24]提出了一种通过局部平衡方程获得横向剪应力的方法。忽略体力,第k层局部平衡方程可表示为
(14)
将式(14)沿z向积分,并强迫横向剪应力满足层间连续条件。横向剪应力可重写为
(15)
式中:Tb为下表面的横向剪应力。
将式(13)代入式(15)中,可得
(16)
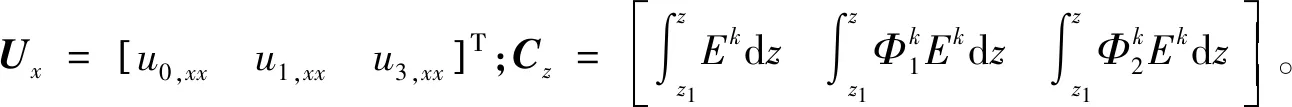
当z=zn+1时,有
Tt(x)=-Tb(x)-CUx
(17)
式中:Tt为上表面的横向剪应力;
由横向剪应力自由表面条件Tt=Tb=0,消去面内位移的二阶导可得
(18)
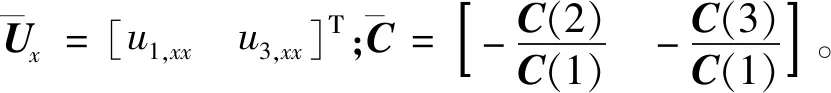
将式(18)代入式(16)中,可得横向剪应力表达式为
(19)
式中:
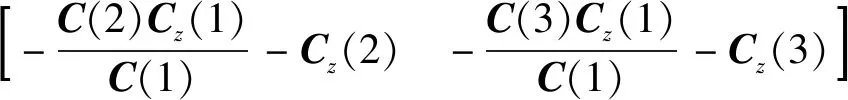
2.5 Reissner混合变分原理和平衡方程
Reissner混合变分原理假定位移和横向剪应力和横向法应力是相互独立。Reissner混合变分原理可以看作Hellinger-Reissner变分原理[42]的特例,可由Hellinger-Reissner变分原理退化得到。Hellinger-Reissner变分原理的总势能函数可表示为
(20)
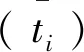
应用拉格朗日乘子法修正式(20)可得
(21)
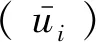
根据Reissner的假定,应变和应力满足本构关系
(22)
式中:Wc(σij)为应变余能密度。
将式(22)代入式(21)中,可得Reissner混合变分原理的总势能函数
ΠR(ui,σij)=
(23)
根据式(22),横向切应变和横向正应变可以写成式(24)的形式[43]
(24)
式中:α=x,y;上标a表示由应变余能密度得到的横向应变。
将式(24)代入式(23),并对式(23)进行变分可得
(25)
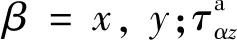
对于层合梁,忽略正应力,Reissner混合变分原理可写为
δWe=0
(26)
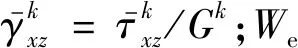
(27)
其中:L为梁的长度;q为横向载荷;Tx0和Tz0分别为梁左端的轴向载荷和剪切载荷;TxL和TzL分别为梁右端的轴向载荷和剪切载荷。
式(26)可以写成
(28)
(29)
将式(12)和式(19)代入式(29)中可得
(30)
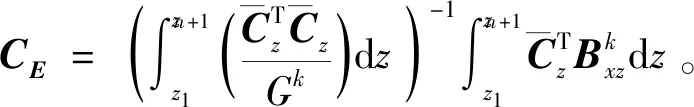
将式(30)代入式(19),可得最终的横向剪应力的表达式
(31)
将式(12)、式(13)和式(31)代入式(28)中,分部积分可得平衡方程
(32)
和在x=0和x=L处的边界条件:
(33)
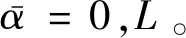
(34)
(35)
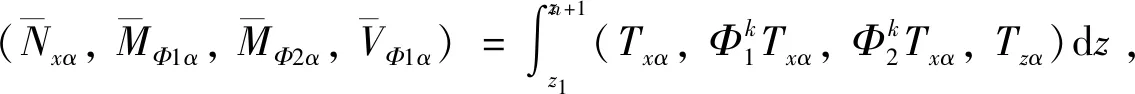
(36)
(37)
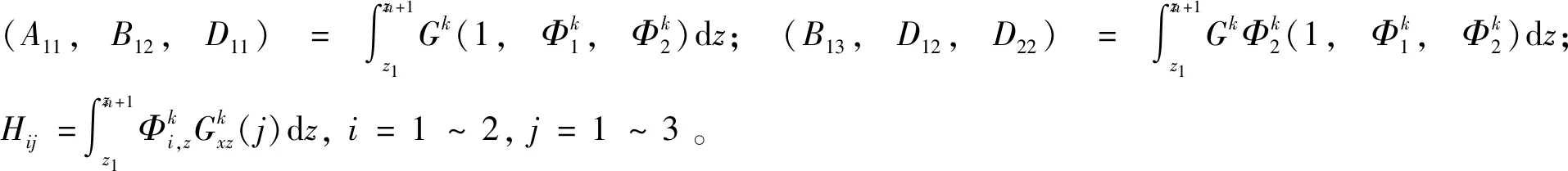
3 算 例
为了测试所提出的新锯齿理论(NZT)的计算精度和稳健性,以层数较多的纤维增强复合材料层合梁和面板,芯层材料属性差异较大的三明治夹层梁以及出现分层的非对称夹层梁为研究对象,考虑静力弯曲特性,给出了上表面承受正弦载荷的简支梁和自由端承受集中载荷的悬臂梁的解析解。计算结果与现有多种理论的计算结果进行了对比。具体包括Pagano[44]提出的精确三维弹性解(Exact),Tahani[45]给出的分层理论解(BLWT),Tessler等[46]给出的高精度有限元的解(2D-FEM)和混合修正锯齿理论解(RZTM)[24],Wu和Chen[30]提出的混合整体高阶锯齿理论解(GHZTM),Ren等[31]提出的C0型锯齿理论解(ZZTC-C0),Han等[47]提出的C0型高阶锯齿理论解(EHOZT),Oate等[48]给出的二维有限元解(PS)和基于修正锯齿理论提出的两节点梁单元的解,基于经典锯齿理论(ZZT)[49]和混合变分原理提出的混合锯齿理论解(ZZTM)、Reddy梁理论解(Reddy)、一阶剪切变形理论解(FSDT)以及基于FSDT和混合变分原理提出的混合一阶剪切变形理论解(FSDTM)。
具体的材料参数如下:
1) 层合梁材料力学特性[50]
E1=25 GPa,E2=E3=1 GPa,G23=0.5 GPa,G12=G13=0.2 GPa,ν12=ν13=ν23=0.25。
2) 夹层梁材料力学特性[46]
下表层:E=73 GPa,G=29.2 GPa;夹芯层:E=0.073 GPa,G=0.029 2 GPa;上表层:E=21.9 GPa,G=8.76 GPa。
3.1 层数较多的简支梁
该算例是承受正弦载荷的简支梁,如图4所示。层合梁每层的厚度和材料性质相同(材料1)。
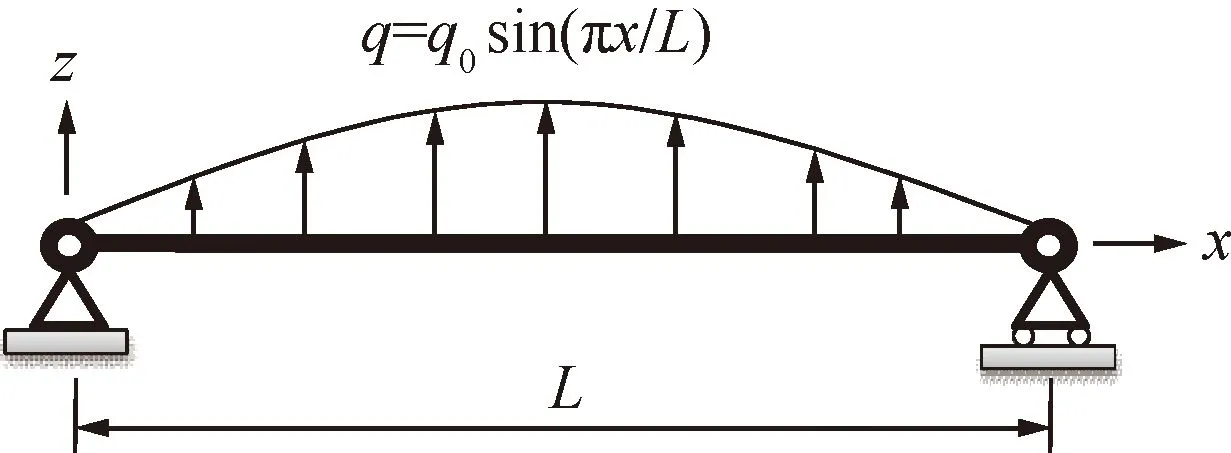
图4 简支梁示意图Fig.4 Schematic of simply supported beam
简支梁的边界条件如下:
x=0,L,w=Nx=MΦ1=MΦ2=0
(38)
满足全部边界条件的位移函数可设为
w0(x)=w00sin(πx/L),
(u0(x),u1(x),u3(x))=
(u00,u10,u30)cos(πx/L)
(39)
位移和应力的无量纲化为
式中:h为梁的厚度。

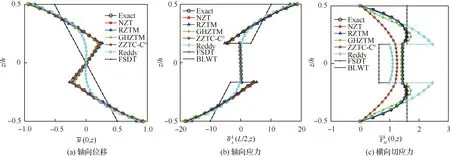
图5 3层梁沿厚度分布的位移和应力对比(L/h=4)Fig.5 Comparison of displacement and stress through thickness of 3-ply beam (L/h=4)
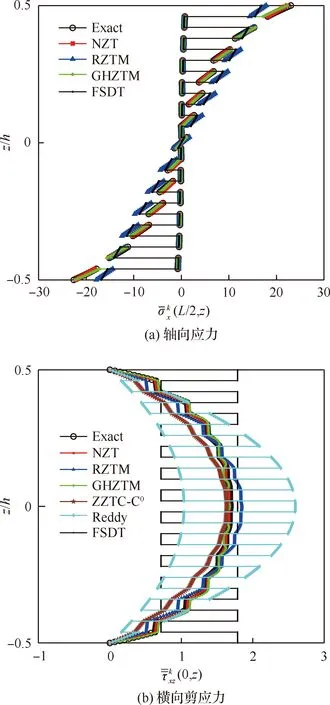
图6 25层梁沿厚度分布的应力对比(L/h=4)Fig.6 Comparison of stress through thickness of 25-ply beam (L/h=4)
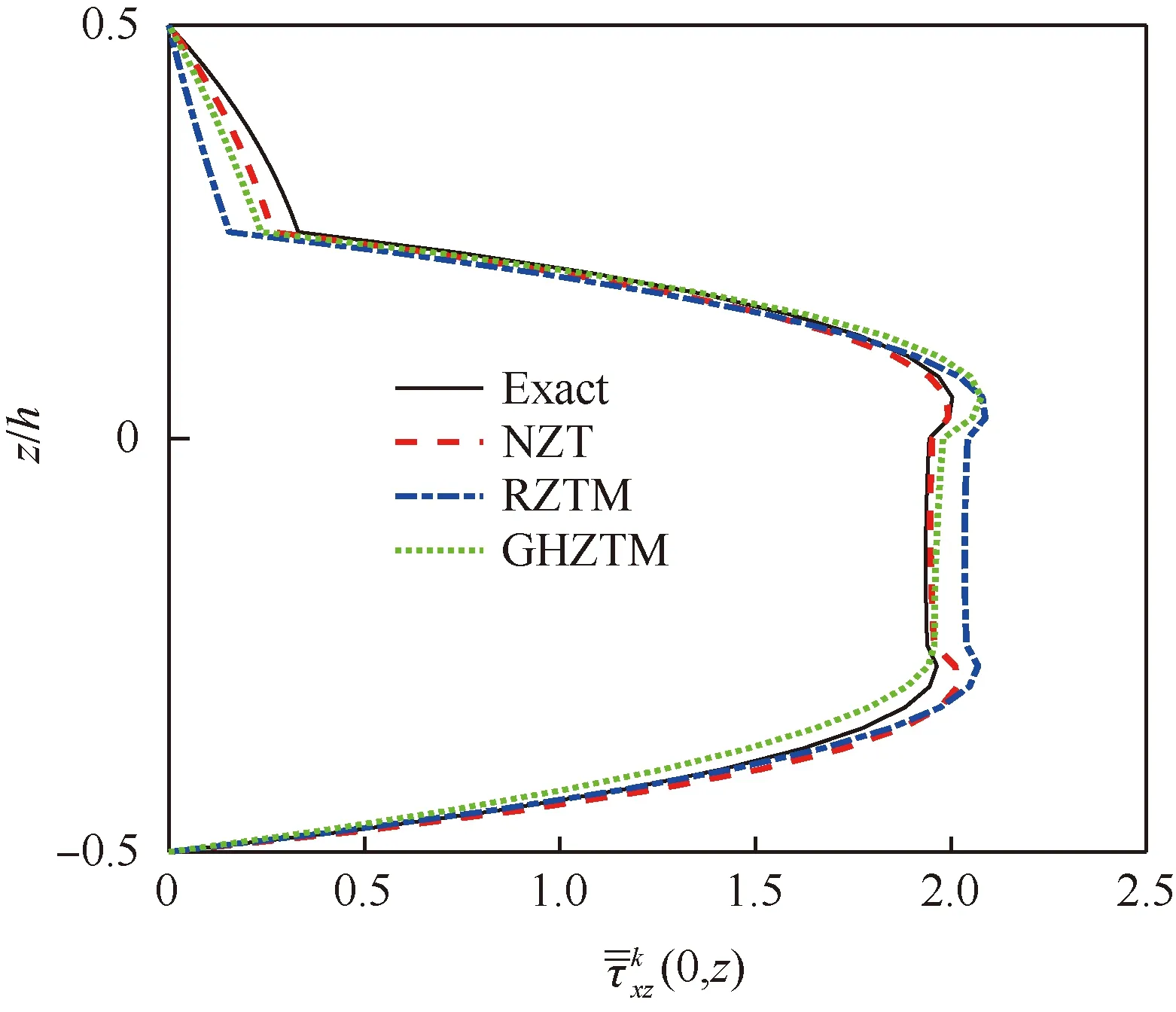
图7 4层梁沿厚度分布的横向剪应力对比 (L/h=4)Fig.7 Comparison of transverse shear stress through thickness of 4-ply beam (L/h=4)
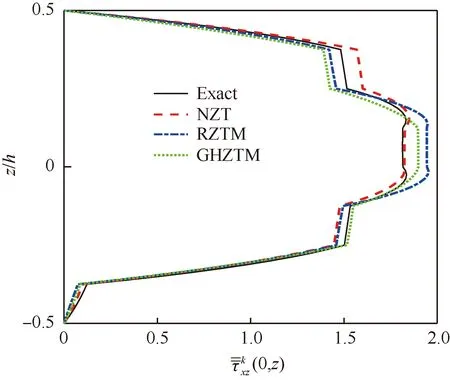
图8 8层梁沿厚度分布的横向剪应力对比 (L/h=4)Fig.8 Comparison of transverse shear stress through thickness of 8-ply beam (L/h=4)
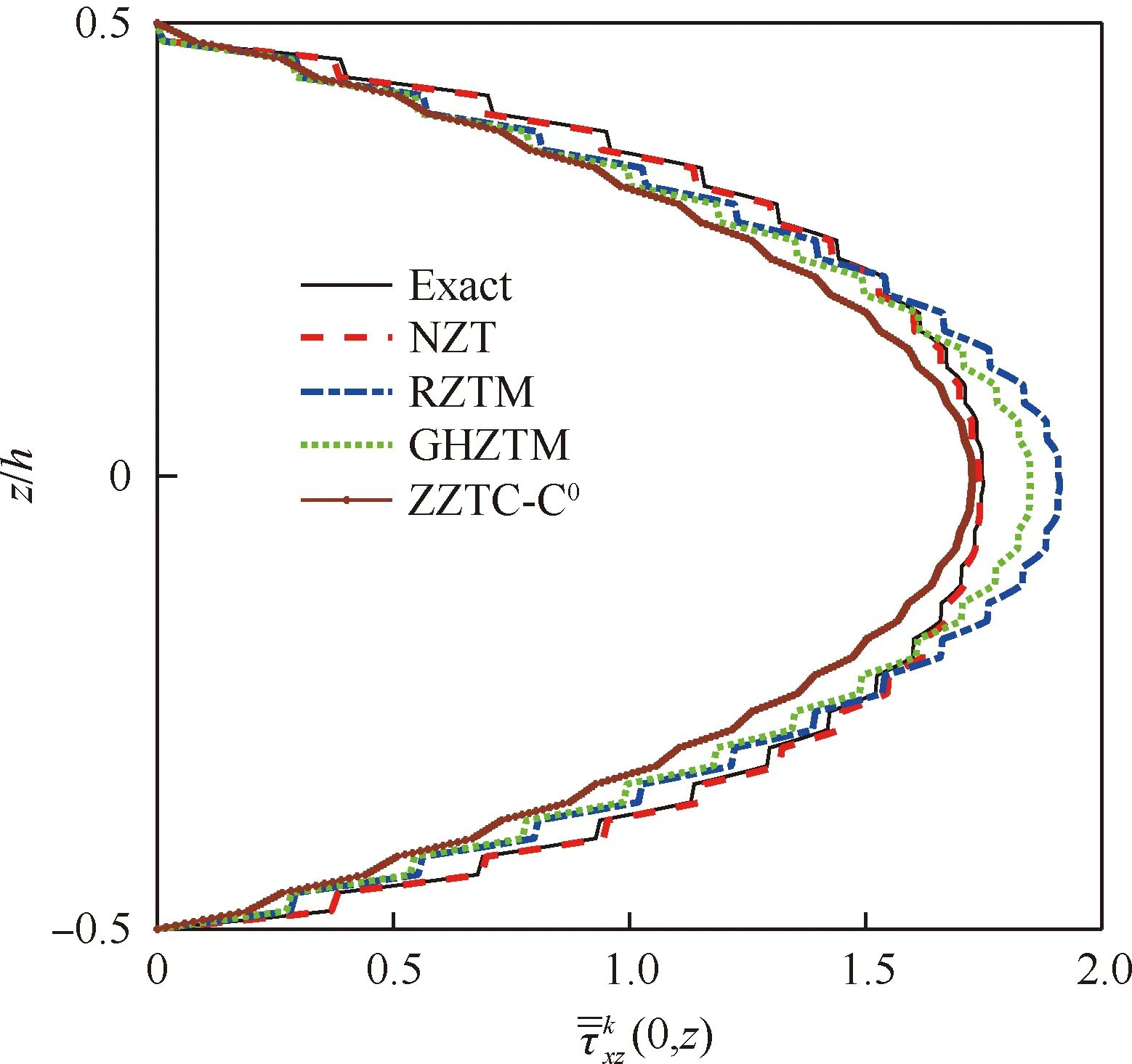
图9 50层梁沿厚度分布的横向剪应力对比(L/h=4)Fig.9 Comparison of transverse shear stress through thickness of 50-ply beam (L/h=4)
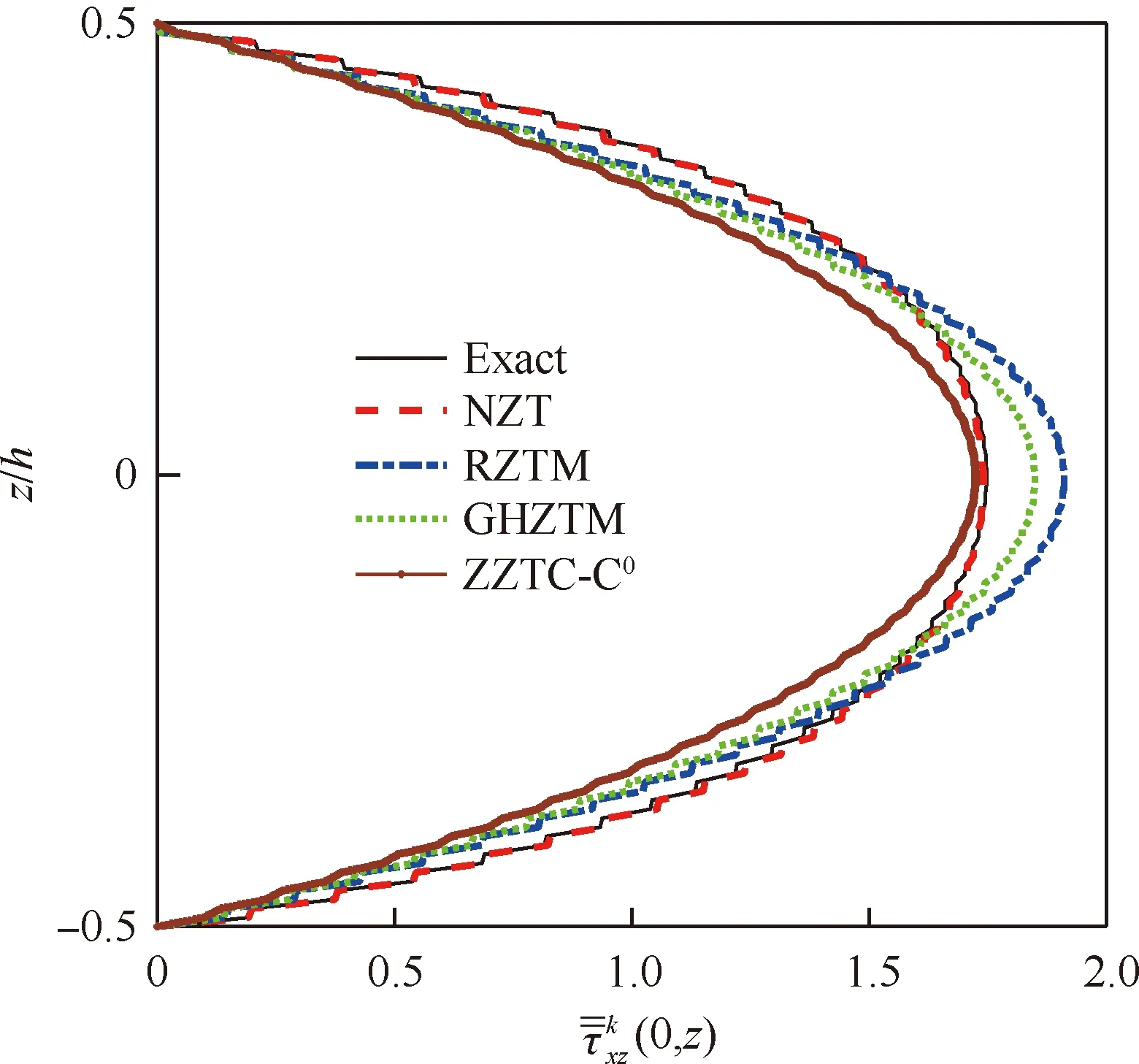
图10 100层梁沿厚度分布的横向剪应力对比(L/h=4)Fig.10 Comparison of transverse shear stress through thickness of 100-ply beam (L/h=4)
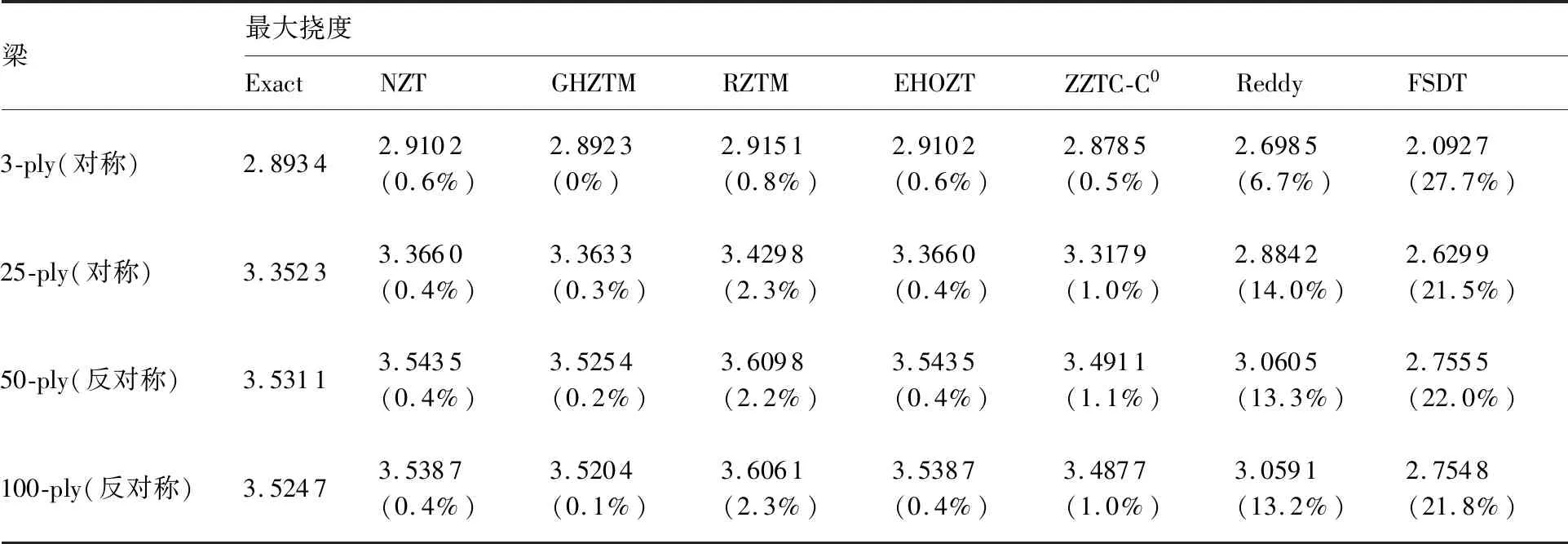
表1 不同梁理论的最大挠度及其相对误差Table 1 Maximum deflection and its relative error of different beam theories
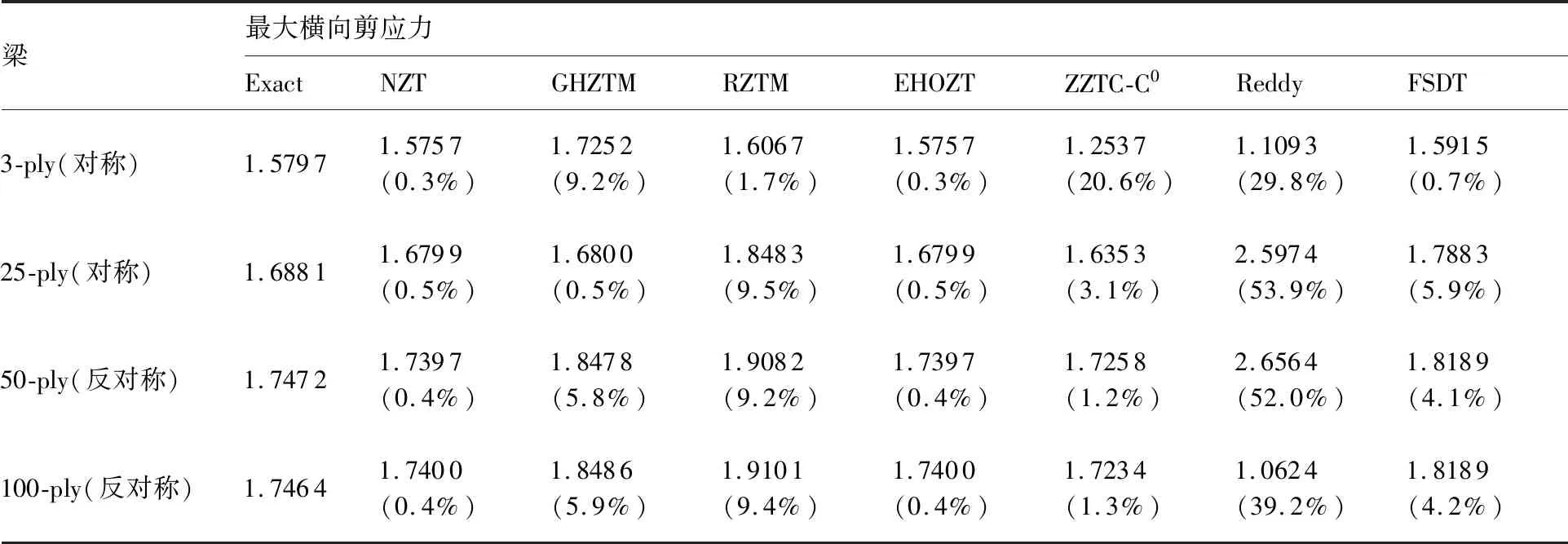
表2 简支梁左端最大横向剪应力及其相对误差Table 2 Maximum transverse shear stress and its relative error at left end of simply supported beam
从表1和表2可以看出,本文提出的NZT的计算结果和三维弹性解(Exact)吻合较好,对4种层合梁,挠度和横向剪应力误差都不超过1%。而一阶剪切变形理论(FSDT)预测挠度误差较大,最大达到27.7%,Reddy梁理论预测横向剪应力的误差较大,最大误差超过50%。RZTM的计算精度会随着层数的增加而降低,当层数由3层增加到25层,RZTM的横向剪应力的误差从1.7%增大到9.5%。当层数超过50层时,GHZTM预测横向剪应力的精度降低。当层数较少时,ZZTC-C0计算横向剪应力误差较大,超过20%。然而,随着层数的增加,ZZTC-C0预测横向剪应力的精度逐渐提高。总结表1和表2分析可得如下结论:相比于FSDT、Reddy和RZTM,提出的NZT的变形和应力的计算精度都有大幅度提升。当层数少时,提出的NZT预测横向剪应力的精度高于ZZTC-C0,当层数较多时,提出的NZT预测横向剪应力的精度高于GHZTM,NZT和EHOZT具有相当的计算精度,表现出较好的稳健性。
综上,本文提出的NZT能够准确地预测对称铺设多层厚梁和层数较多的反对称铺设多层厚梁的挠度和应力。对于层数较少的反对称铺设层合厚梁横向剪应力,NZT具有一定的误差,但误差随着层数的增加,逐渐减小。
3.2 面板和芯层材料属性差异较大的三明治悬臂夹层梁
准确地预测面板和芯层材料属性差异较大的夹层梁的变形和应力十分困难,Tessler提出的RZTM很好地解决了该难题。本文提出的新锯齿理论模型不仅能够准确地预测层数较多的复合材料层合梁的变形和应力,对该类结构也具有较好的预测精度。这里以3层软核夹层悬臂梁为例,每层厚度为(0.1h/0.8h/0.1h),夹层梁每层具有不同的材料性质(材料2)。悬臂梁在自由端承受横向载荷F,如图11所示。
边界条件为
x=0,u0=u1=u3=w0=0
x=L,Nx=MΦ1=MΦ2=0,VΦ1=F
(40)
满足全部边界条件的位移函数[32]可设为
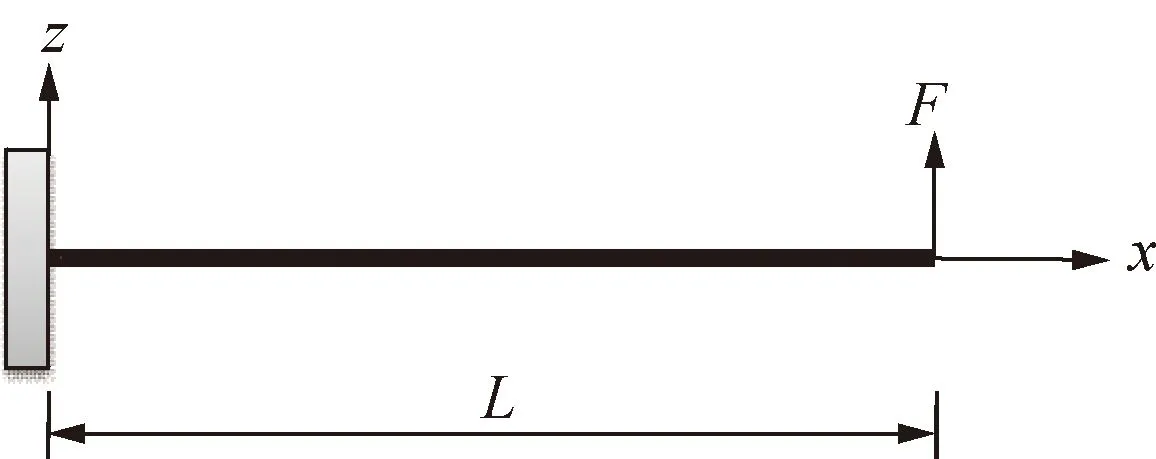
图11 悬臂梁示意图Fig.11 Schematic of a cantilevered beam
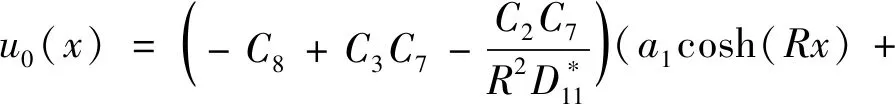
u3(x)=a1cosh(Rx)+a2sinh(Rx)+a3
w0(x)=
(41)
式中:
其中:C2/C1<0,如果C2/C1>0,则式(41)中的双曲正弦函数和双曲余弦函数分别改为正弦函数和余弦函数即可。
位移和应力的无量纲化为
图12和图13分别给出了应力沿厚度方向分布图和中面挠度沿轴向分布图。从图12和图13可以看出,一阶剪切变形理论(FSDT)严重低估了最大挠度和最大轴向应力,挠度最大误差可达到82%,轴向应力最大误差可达到76.5%。受FSDT直法线假定的限制,即使使用混合变分原理进行修正,混合一阶剪切变形理论(FSDTM)同样具有较大的误差。图12(b)中的2D-FEM解是使用Abaqus软件计算得到,梁模型使用20万(1 000(长)×200(高))个4节点,平面应力,完整积分,CPS4单元进行离散。结果显示本文提出的NZT与2D-FEM解吻合较好,具有较高的精度。
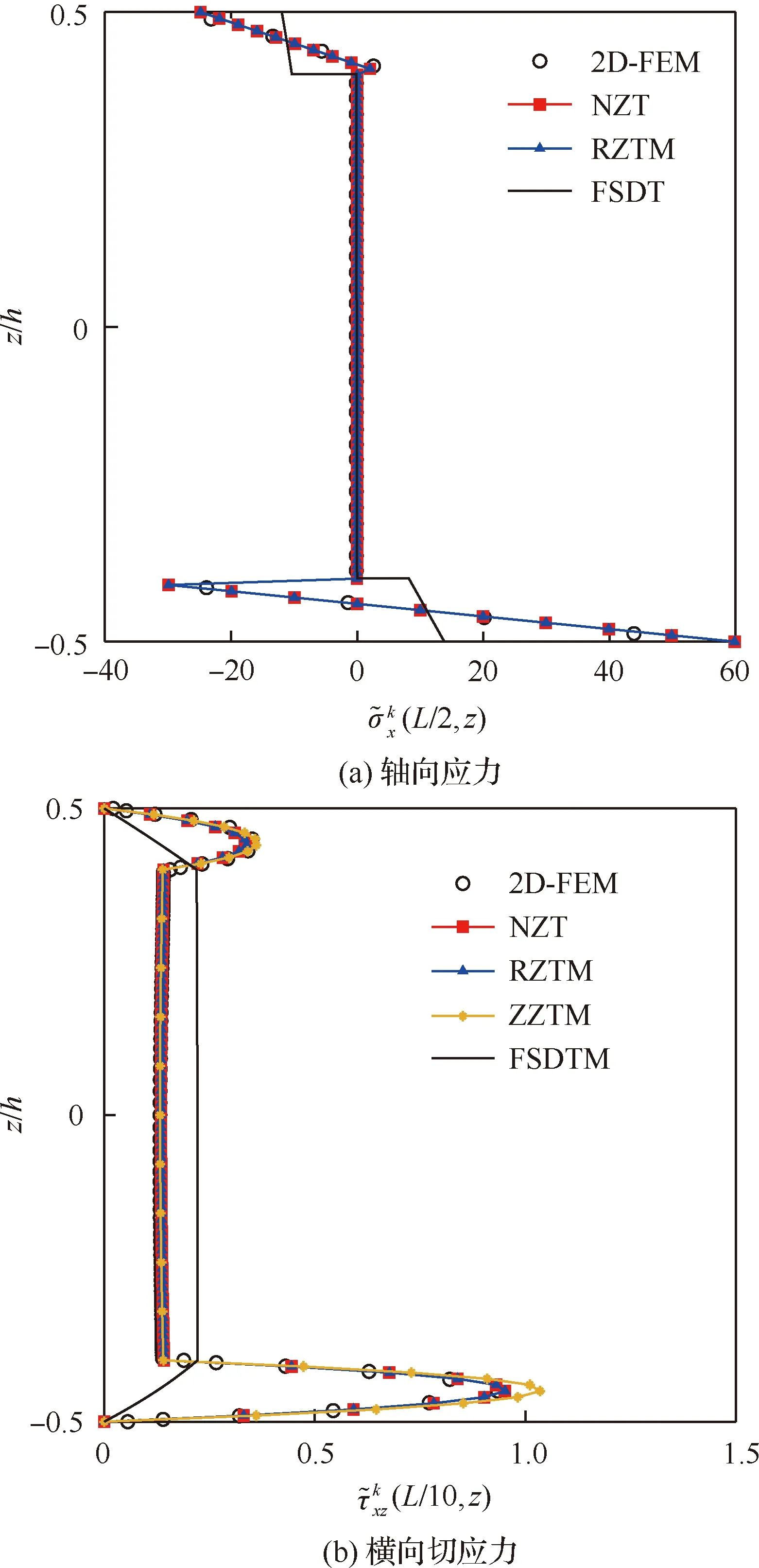
图12 沿悬臂梁厚度分布的应力对比(L/h=5)Fig.12 Comparison of stress through thickness of a cantilevered beam (L/h=5)
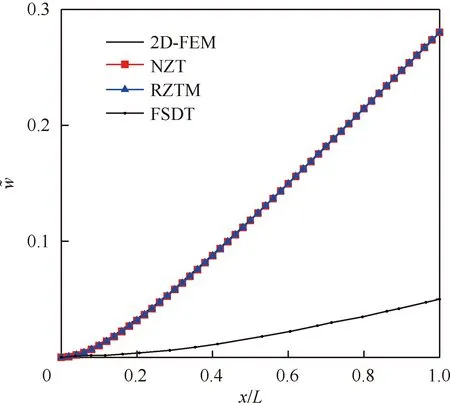
图13 沿悬臂梁跨度分布的挠度对比(L/h=5)Fig.13 Comparison of deflection along cantilevered beam span (L/h=5)
3.3 考虑分层的非对称悬臂层合梁
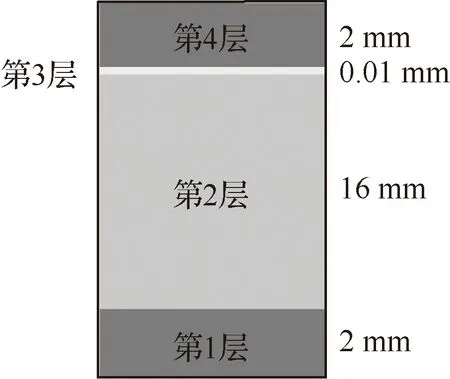
图14 分层的梁截面示意图Fig.14 Diagram of beam section for delamination
表3 材料力学特性
Table 3 Mechanical properties of materials
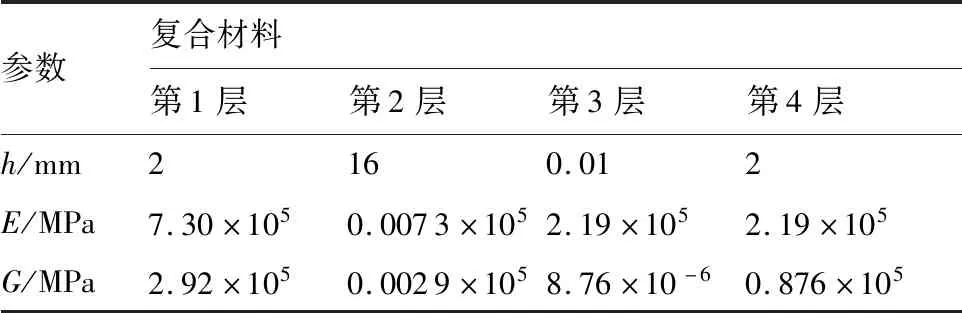
参数复合材料第1层第2层第3层第4层h/mm2160.012E/MPa7.30×1050.0073×1052.19×1052.19×105G/MPa2.92×1050.0029×1058.76×10-60.876×105
表4 在x=L处的挠度Table 4 Deflection at x=L
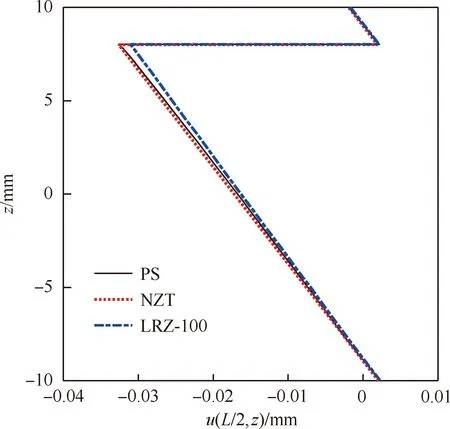
图15 发生分层的悬臂梁轴向位移对比(L/h=5)Fig.15 Comparison of axial displacement for a delamination cantilevered beam (L/h=5)
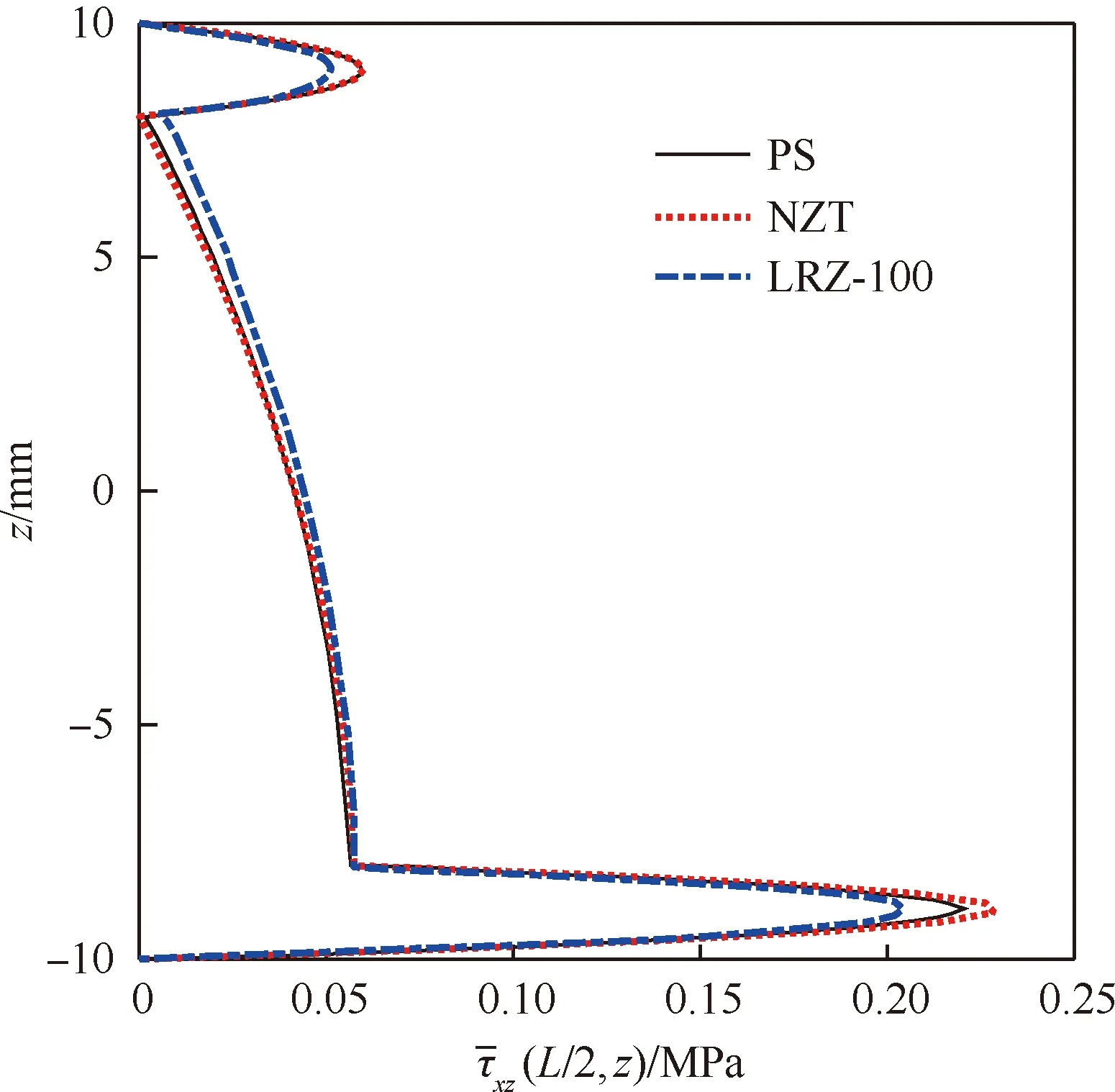
图16 发生分层的悬臂梁横向剪应力对比 (L/h=5)Fig.16 Comparison of transverse shear stress for a delamination cantilevered beam (L/h=5)
4 结 论
本文通过构造一个新的线性分段锯齿函数,提出了一种能够准确预测层合梁结构横向剪应力的新锯齿理论模型(NZT)。为了验证该理论模型精度,计算了层数较多的简支梁、材料属性差异较大的三明治悬臂梁以及发生分层的非对称悬臂梁的位移和应力。可得到如下结论:
1) 新锯齿函数具备描述每层材料变化和不同横截面处变化规律不同的能力,使得NZT能够准确预测横向各向异性的多层梁的变形和应力。
2) NZT位移场中仅含有4个与层数无关的未知量,不含有横向位移的一阶导数,构造梁单元时,仅需使用C0插值形函数。
3) NZT能够预先满足横向剪应力层间连续,无需后处理就能够准确预测层合梁的层间应力。
4) 算例结果显示:NZT能够准确预测层数较多的层合梁和材料属性差异较大的三明治夹层梁的变形和应力,能够准确预测层合梁的分层。
