面向空中目标威胁评估的多传感器管理方法
2019-12-09张昀普单甘霖
张昀普,单甘霖
陆军工程大学石家庄校区 电子与光学工程系,石家庄 050003
随着科学技术的发展,现代战争的主流已演变成以“网络中心战”为核心的信息战争,这也为传感器系统的有效使用提出了更高的要求[1]。由于信息战争中作战节点错综复杂,信息量巨大且形式多样,传感器系统往往在操作、部署位置和算法逻辑等多方面存在约束,致使系统处理信息的难度大大增加,因此,需要对传感器系统进行有效的管理,以使作战收益最大化。随着传感器管理理论研究不断深入,人们开始将研究重点放在贝叶斯意义上的最优管理方法上[2],截止目前,共发展为3类基于贝叶斯理论的传感器管理方法,即基于任务的管理方法[3-4]、基于信息论的管理方法[5-6]和基于风险的管理方法[7]。
这3类方法均设定一个与作战密切相关的目标函数以使所需求的收益达到最大。前两种方法更多关注的是通过传感器管理使一项或多项战术指标达到最优,如目标跟踪精度[8]、后验克拉美罗下界[9]、Rényi信息增量等[10-11]。但在有些情况下,宁可不追求这些战术指标的最优值,也要使作战风险达到最小。例如,文献[12]指出,当对目标进行跟踪时,利用前两种管理方法可以得到极佳的目标跟踪精度,但是如果不需要打击目标,仅使传感器不丢失目标即可,而不是一味地追求高的跟踪精度,此时需通过传感器管理使目标的丢失风险达到最小。因此,基于风险的管理方法将关注重点放在了控制作战风险上,通常认为风险是由作战决策所造成的潜在损失及其发生的概率所决定的,执行传感器管理的目的是降低作战风险以使损失达到最小,该类方法具有良好的实际应用价值,已成为传感器管理领域内的研究热点。文献[13]建立了面向目标检测的风险模型,认为由于传感器漏警概率的存在,在检测时会产生相应的漏警风险,并提出一种基于最小贝叶斯风险的传感器管理方法使漏警所造成的损失达到最低。文献[14]研究了目标识别背景下的传感器管理问题,认为识别结果的不准确性会导致指挥员做出错误的决策,从而产生相应的风险,并建立了基于观测值校正的风险函数模型,提出了相应的传感器管理方法。文献[15]认为在对目标进行威胁评估时,目标的威胁度是一个与目标状态相关的函数,并以威胁度分布的方差量化威胁评估风险。
但文献[15]中仅以威胁度分布的方差量化威胁评估风险是不够准确的,在实际中,对于目标威胁度不同程度的误判所造成的损失应是不同的,例如在我方防御资源充足的情况下,当把高威胁的目标错判为低威胁时,我方会对其分配较少的防御资源,从而可能使我方受到致命的火力打击,但把低威胁的目标错判为高威胁时,可能仅会造成一些防御资源的浪费,比上一种情况的损失要小得多。因此,在建立威胁度模型时,需将威胁度不确定性与误判损失相结合,使模型更具有实际价值。
同时,以有源雷达为代表的主动传感器作为获取战场信息的重要工具,其探测距离远且具有较高的距离分辨力,可实现对目标的高精度量测,但在工作时会辐射电磁波,容易暴露位置,因此需要在执行任务时对主动传感器的辐射风险进行控制,以提高其战场生存能力。合理量化传感器的辐射状态是控制辐射风险的前提,文献[16-17]利用传感器发射功率、目标回波功率和接收机接收灵敏度等参数计算出传感器辐射被截获的概率,并以此表示传感器在每一时刻的辐射状态。但在实际中目标参数很难获取,故该方法的实用性较差。文献[18-19]采用辐射度影响(Emission Level Impact,ELI)替代了截获概率,其表示传感器被敌方接收机累积接收的辐射量,在使用时不需要获取目标相关参数,具有较好的实际应用价值。
针对上述问题,本文面向空中目标威胁评估任务,以多主动传感器系统为研究对象,在不改变传感器结构和空间位置的条件下,提出一种基于风险的多传感器管理方法,旨在最小化由威胁评估结果的不准确性和传感器辐射所带来的潜在损失。首先建立了基于部分可观马尔可夫决策过程(Partially Observable Markov Decision Process,POMDP)的传感器管理模型;然后提出了基于信息状态的威胁评估风险和辐射风险的预测方法;并以二者加权和最小为优化目标建立了长期目标函数,最后设计了一种基于分支定界的决策树搜索算法以求解该问题。仿真结果证明了所提搜索算法和管理方法的有效性和合理性。
1 基于POMDP的传感器管理模型
本文任务场景描述如图1所示。假设我方共部署M个传感器对N个空中目标进行威胁评估,并将获取的量测信息发送给控制中心,我方控制中心制定相应的传感器管理方案,并向整个传感器系统发布命令以控制各传感器工作。
由于在整个过程中传感器的量测不确定性和目标运动状态的随机性,所以本文研究的传感器管理问题是一个不确定信息下的决策问题,而POMDP是一种研究随机环境下多阶段决策的理论方法[20],故可以基于该理论对该问题进行建模,其基本组成要素分为系统动作、系统状态、状态转移函数、系统观测、观测函数和收益函数。
1.1 系统动作
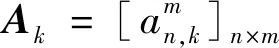
考虑到传感器在时间和空间上配准较为困难,为简便计算,本文设定在同一时刻一部传感器只能量测一个目标,且一个目标只能被一部传感器所量测,则系统动作的约束可描述为
(1)
1.2 系统状态及状态转移函数
定义k时刻系统状态Sk=[Xk,Ek],由目标的运动状态和传感器的辐射状态组成。
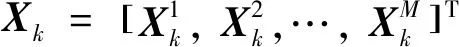
(2)
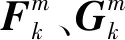
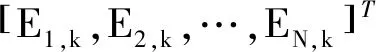
Tn,k=[p(En,k=j|En,k-1=i)]i,j∈{0,1,…,Emax}
(3)
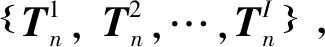
(4)
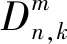
若该传感器不工作,Tn,k为单位阵。
1.3 系统观测及观测函数
定义k时刻系统的观测集合Zk=[ZXk,ZEk],由目标信息和传感器瞬时辐射量的观测值组成。
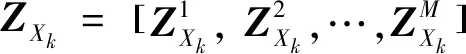
(5)
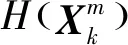
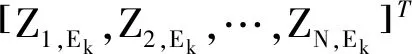
W(Zn,Ek=c)=[p(Zn,Ek=c|En,k=j,
En,k-1=i)]i,j∈{0,1,…,Emax}c∈{0,1,…,Cmax}
(6)
若该传感器不工作,其观测矩阵为单位阵。
1.4 收益函数
传感器管理的核心在于对未来时刻内的收益进行预测,并以收益达到最佳为目标制定相应的管理方案。结合目标威胁评估任务,同时考虑威胁评估风险和传感器的辐射风险,可得一步收益函数为
R(Ak)=ωU(Ak)+(1-ω)Y(Ak)
(7)
式中:R(Ak)、U(Ak)和Y(Ak)分别为在执行分配方案Ak后,在k+1时刻的总风险、威胁评估风险和辐射风险;ω为平衡系数,用来权衡两种风险。
进一步,多步收益函数的表达式为
(8)
式中:H为决策步长。
2 风险预测方法
通过1.4节可知,对威胁评估风险和辐射风险进行预测是制定传感器管理方案的核心,因此,需要对两种风险进行合理量化和准确预测。
2.1 威胁评估风险
目标的威胁度是一个随着目标状态变化的随机变量,在威胁评估的过程中,会将目标状态的不确定性传递到威胁度上来,使威胁等级评估的结果难以精确,从而产生相应的评估风险。
2.1.1 威胁评估方法
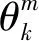
(9)
式中:xp、yp和zp为防御阵地中心的三坐标。
构建各影响因素对应的子威胁度函数,从而将目标状态的估计映射到威胁上来。
1) 目标距离
(10)
式中:d0为子威胁度极值点对应的距离;fd为距离系数,用来调节子威胁度函数值与距离的变化倍率。
2) 目标速度
(11)
式中:v0为子威胁度极值点对应的速度;fv为速度系数。
3) 航向角
(12)
式中:fα为角度系数。
在得到各因素对应的子威胁度后,通过加权的方式计算目标m的威胁度
(13)
式中:ωd、ωv和ωα分别为距离、速度和航向角的权重。
在实际战场上,需要根据威胁度得到目标的威胁等级,以使指挥员更直观的了解目标的威胁性。本文设置3类威胁等级,记为1(低等级)、2(中等级)和3(高等级)3类,其对应规则为
(14)
式中:θ2和θ3分别为威胁等级分界点所对应的威胁度。
2.1.2 基于信息状态的威胁风险预测方法
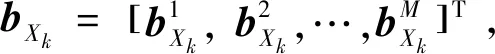
(15)
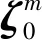
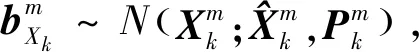
由于信息状态为高斯分布,在非线性变换后难以获得其分布律的解析解,故本文在计算威胁度时先使用蒙特卡罗方法依照信息状态分布获取一定数量的目标状态样本点,再通过计算各样本点对应的威胁度得到相应的威胁度概率分布,从而近似估计目标的威胁等级和威胁评估风险。其过程如下:
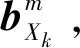
步骤2采样。依据目标m在k+1时刻的信息状态分布获取L个样本点(L为任意值,其值越大,威胁度评估的结果就越准确,但会影响计算速度)。
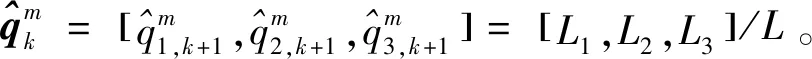
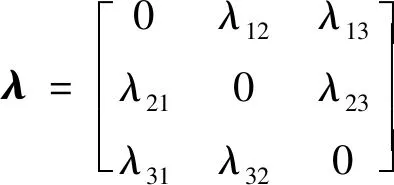
步骤5预测一步威胁评估风险。结合传感器的分配方案Ak,可得一步威胁评估风险的预测值为
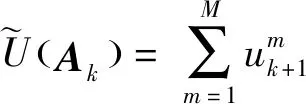
(16)
步骤6预测多步威胁评估风险。令k=k+1,转到步骤1,进行H-1次循环后(H为决策步长),计算结束,得到多步威胁评估风险的预测值为
(17)
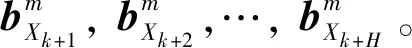
2.2 基于信息状态的辐射风险预测方法
和目标运动状态相同,传感器的ELI状态无法完全预知,因此引入ELI信息状态bEk=[b1,Ek,b2,Ek,…,bN,Ek]T。对于任意的传感器n,其在k时刻的信息状态为
(18)
假设在k+1时刻传感器n处于工作状态,且已知相应的瞬时观测辐射等级Zn,Ek+1的具体值,则可利用隐马尔可夫模型滤波器更新其ELI信息状态[18]:
(19)
式中:⊙为Hadamard积;1为Emax维单位向量。
若该传感器不工作时,其ELI信息状态不发生转移。
然而在实际中,在k时刻无法预测k+1时刻Zn,Ek+1的具体值,但是可以根据信息状态得到其概率分布:
p(Zn,Ek+1|bn,Ek)=
p(En,k+1|En,k)bn,Ek=
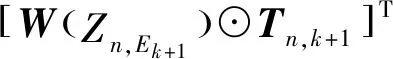
(20)
根据式(19)和式(20),可求出传感器n在k+1 时刻的预测信息状态:
p(Zn,Ek+1|bn,Ek)=
(Tn,k+1)Tbn,Ek
(21)
根据ELI值与被截获概率的关系,得到该传感器在k+1时刻的被截获概率:
(22)
当我方传感器被敌方截获时,将有可能遭受火力打击,从而产生传感器资源损失。因此,本文定义在k+1时刻传感器n的辐射风险预测值为
(23)
式中:on∈O=[o1,o2,…,oN],代表传感器的战术价值,属于先验信息。
结合我方传感器的分配方案,可得一步辐射风险预测值为
(24)
根据式(21),可求出传感器n的多步预测信息状态为
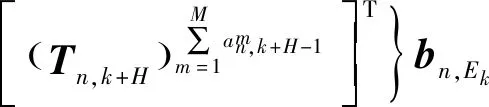
(25)
进一步,可得多步辐射风险预测值为
(26)
3 优化求解
3.1 目标函数
传感器管理在决策周期上可分为短期和长期两种管理方法,短期方法以未来一步的收益函数为决策依据,尽管实现简单,但忽视了系统动作对未来系统状态的影响,管理效果欠佳。而长期方法以多步收益函数为决策依据,其管理效果要优于短期管理[8]。为追求更高的作战收益,本文采用长期管理方法,以H为决策步长,建立相应的目标函数为
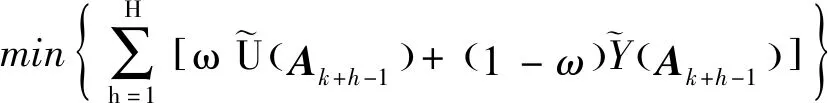
(27)
该目标函数的最优解为[Ak,Ak+1,…,Ak+H-1]opt,代表时域[k+1,k+H]上的最优管理方案。
由于该问题是一个多决策步长、系统动作连续的POMDP问题,在求解时计算复杂度过大。为了满足实际战场上对于决策的实时性要求,本文将传感器管理问题转化为决策树,提出一种基于分支定界的UCS(Uniform Cost Search)算法以快速获得最优解。
3.2 基于分支定界的UCS算法
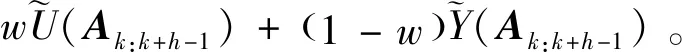
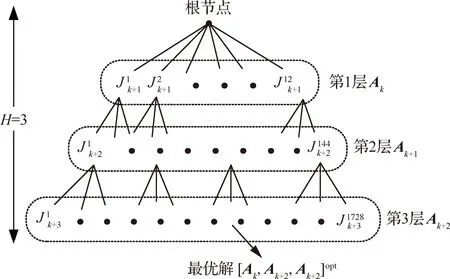
图2 决策树示意图Fig.2 Decision tree diagram
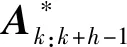
(28)
由于在单一运动模型下传感器性能的稳定性和目标跟踪的持续性,目标状态的最优估计误差通常不会较前一时刻有太大变化[24]。由于威胁评估风险仅与目标状态有关,因此其在大多时候也不会发生突变,通过大量仿真发现,下一时刻的威胁评估风险通常是上一时刻的0.8~1.2倍,因此,可得
(29)
(30)
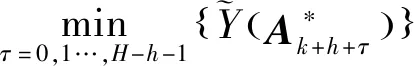
因此,可得
(31)
根据式(28)、式(29)和式(31),得该节点的下界值为
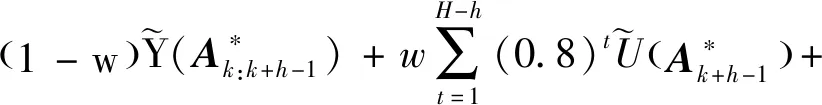
(32)
得到节点的下界值后,即可以在UCS的过程中通过分支定界方法及时删除多余的节点,加快搜索速度。基于分支定界的UCS搜索算法流程如下所示:
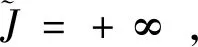
步骤2
1) 若列表不为空
打开列表中第一个节点并将其删除。
① 若此时未到达最底层H
② 若此时已到达最底层H
2) 若列表为空
转到步骤3
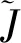
4 仿真实验

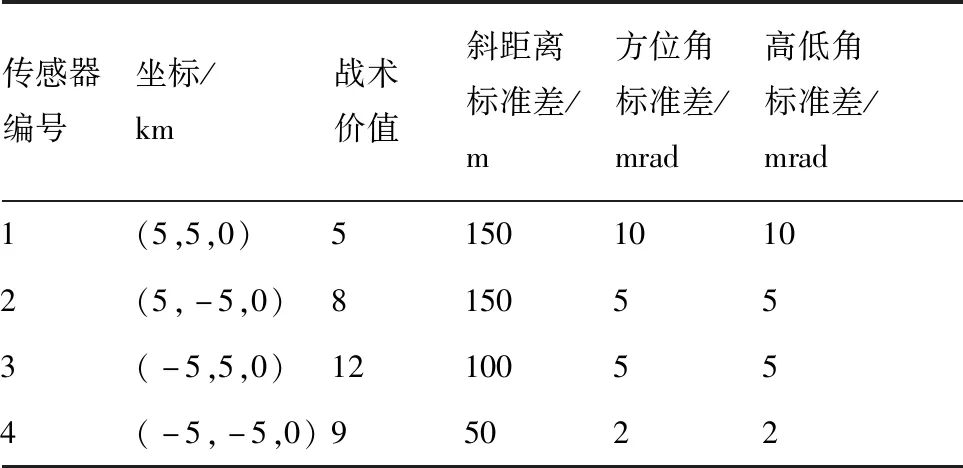
表1 传感器参数Table 1 Parameters of sensors
将传感器的ELI状态量化为{0,1,2,3,4},0为无辐射,对应被截获概率为0%,1为低辐射等级,对应被截获概率为0%~25%,2为中辐射等级,对应被截获概率为25%~50%,3为高辐射等级,对应吗 被截获概率为50%~75%,4为极高辐射等级,对应被截获概率为75%~100%。设定每个传感器有3个ELI状态转移矩阵,为了不失一般性,设定在相同的目标距离范围内量测精度高的传感器更容易处于高ELI等级,各传感器的ELI状态转移矩阵为
传感器与目标距离小于5 km时:
传感器与目标距离位于5~15 km时:
传感器与目标距离大于15 km时:
4.1 确定平衡系数和决策步长
平衡系数w的作用在于权衡威胁评估风险和辐射风险对于总风险的影响。本文在H=1下研究了不同平衡系数对两种风险的影响,并以此为依据确定w。图3给出了不同平衡系数下的传感器对目标1的分配方案,图4描述了平衡系数的变化对归一化威胁评估风险和辐射风险的影响。从图3可以看出,平衡系数的改变会使管理方案发生相应的变化,从而影响的风险控制效果。结合图4可知,随着平衡系数的增大,威胁评估风险越来越小,辐射风险越来越大,说明所制定的管理方案越来越注重控制威胁评估风险,而渐渐忽视辐射风险。当w<0.45时,辐射风险远小于威胁评估风险,当w>0.45时,威胁评估风险远小于辐射风险,这两种情况均会造成两种风险的失衡,无法兼顾评估结果的准确性和传感器的生存。当w=0.45时,二者十分接近,说明此时所制定的管理方案兼顾了两种风险的影响,使二者可以达到相对平衡,因此在接下来的仿真中选取w=0.45。
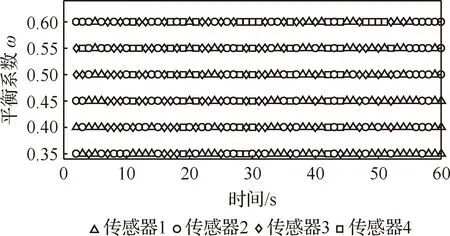
图3 不同平衡系数下传感器对目标1的分配方案Fig.3 Assignment scheme of sensors to target 1 under different equilibrium coefficients
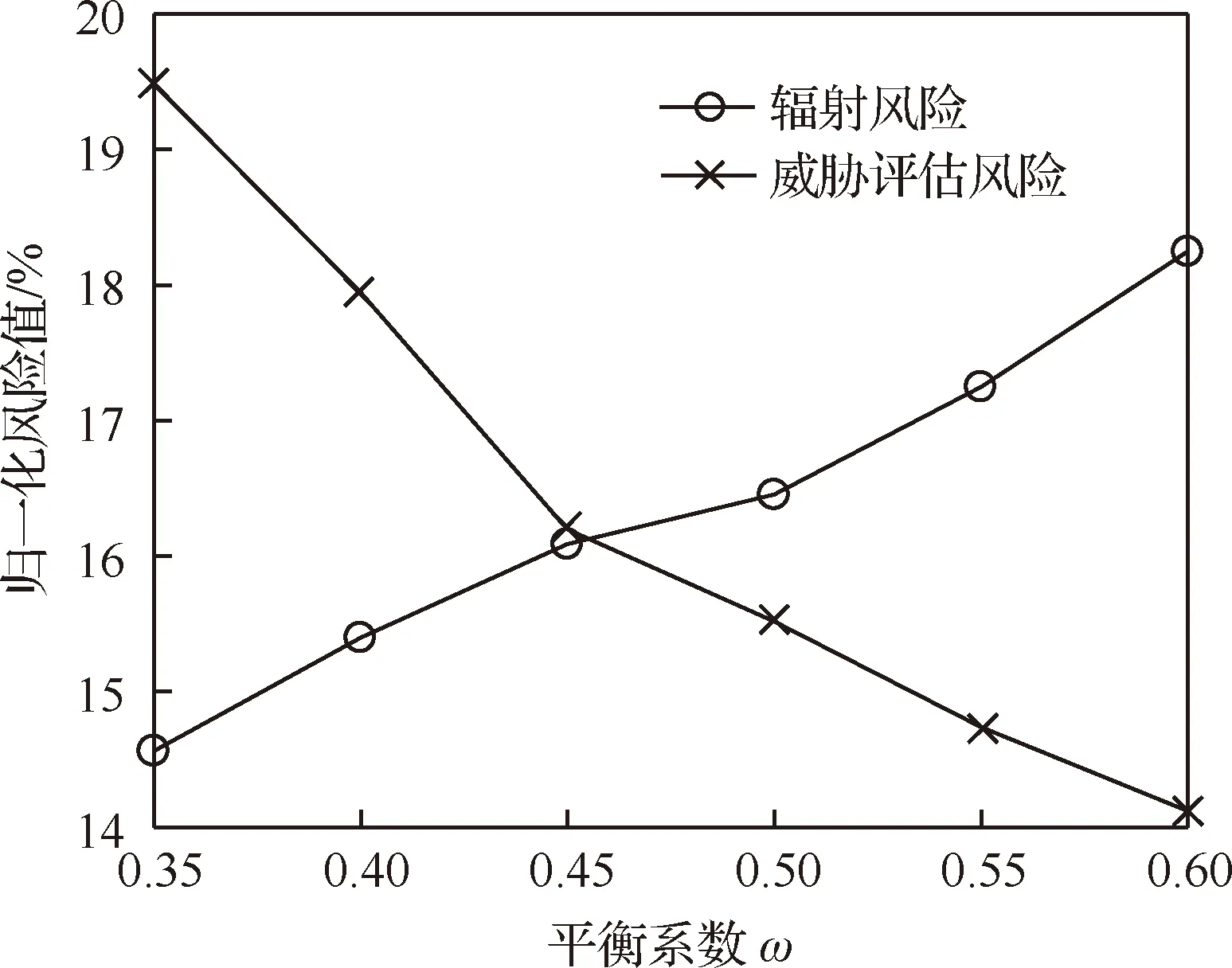
图4 不同平衡系数下的归一化风险值Fig.4 Normalized risk under different equilibrium coefficients
图5为当w=0.45时,不同决策步长下累积总风险值的对比图。可以看出,在H=2到H=6时,随着H的增加,累积总风险值越来越小,说明系统能够获得更优的管理方案。但当H=7时,累积风险值相较于H=6时不降反增,这是因为随着决策步长的增加,对于系统状态的预测变得越来越不准确,计算的误差就会越来越大,从而使总风险有所增加,因此,一味增大决策步长是没有意义的。同时,虽然在H=6时的累积风险值最小,但其与H=4时的风险值相差不多,且由于步长的增加会导致计算复杂度的大幅增长,为了兼顾风险控制效果和计算量,本文在接下来的仿真中选取决策步长H=4。
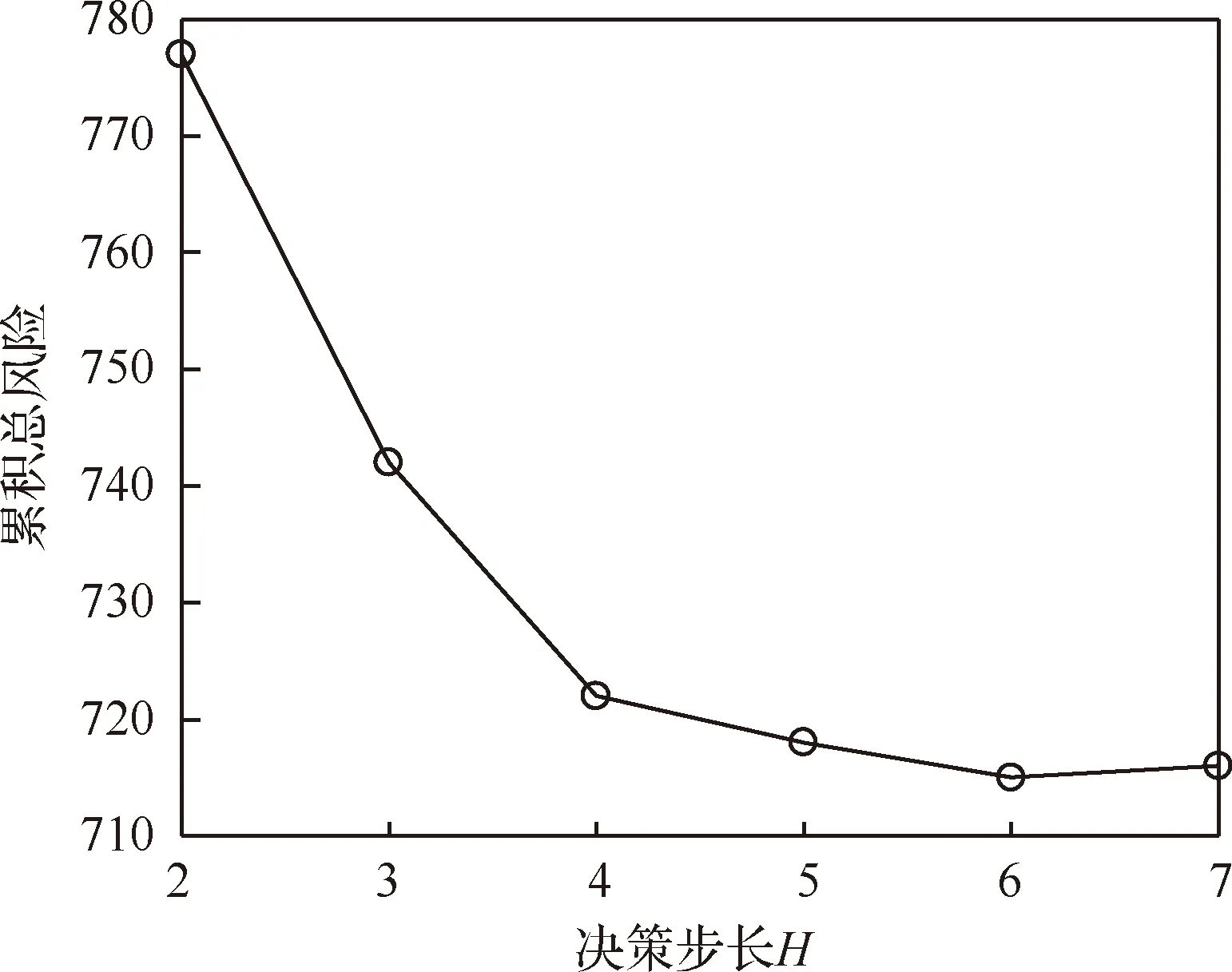
图5 不同决策步长下的累积总风险Fig.5 Cumulative total risk value under different decision time steps
4.2 算法性能对比
为了验证本文提出的基于分支定界的UCS算法(BB-UCS)的优势,采用穷举搜索(Enumerative Search, ES)和UCS算法进行对比。表2为不同算法的性能指标对比,其中,打开节点百分比数和最大存储节点数越小,代表算法的搜索时间和内存消耗越少[25],总风险值越小,代表算法的求解质量越高,图6为UCS和本文算法的节点打开百分比的对比图。
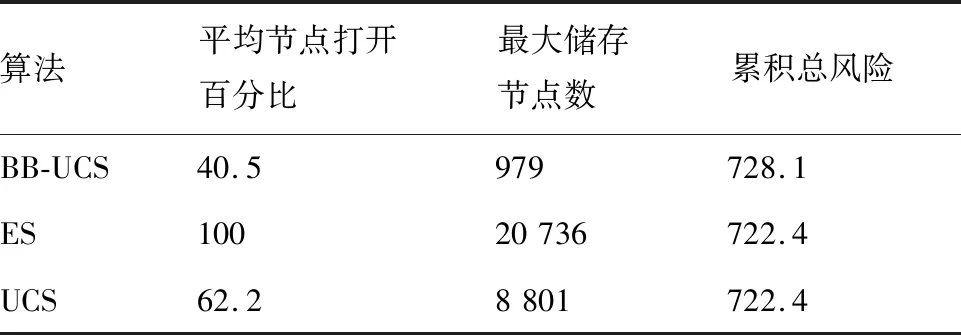
表2 不同算法搜索性能对比Table 2 Comparison of search performance under different algorithms
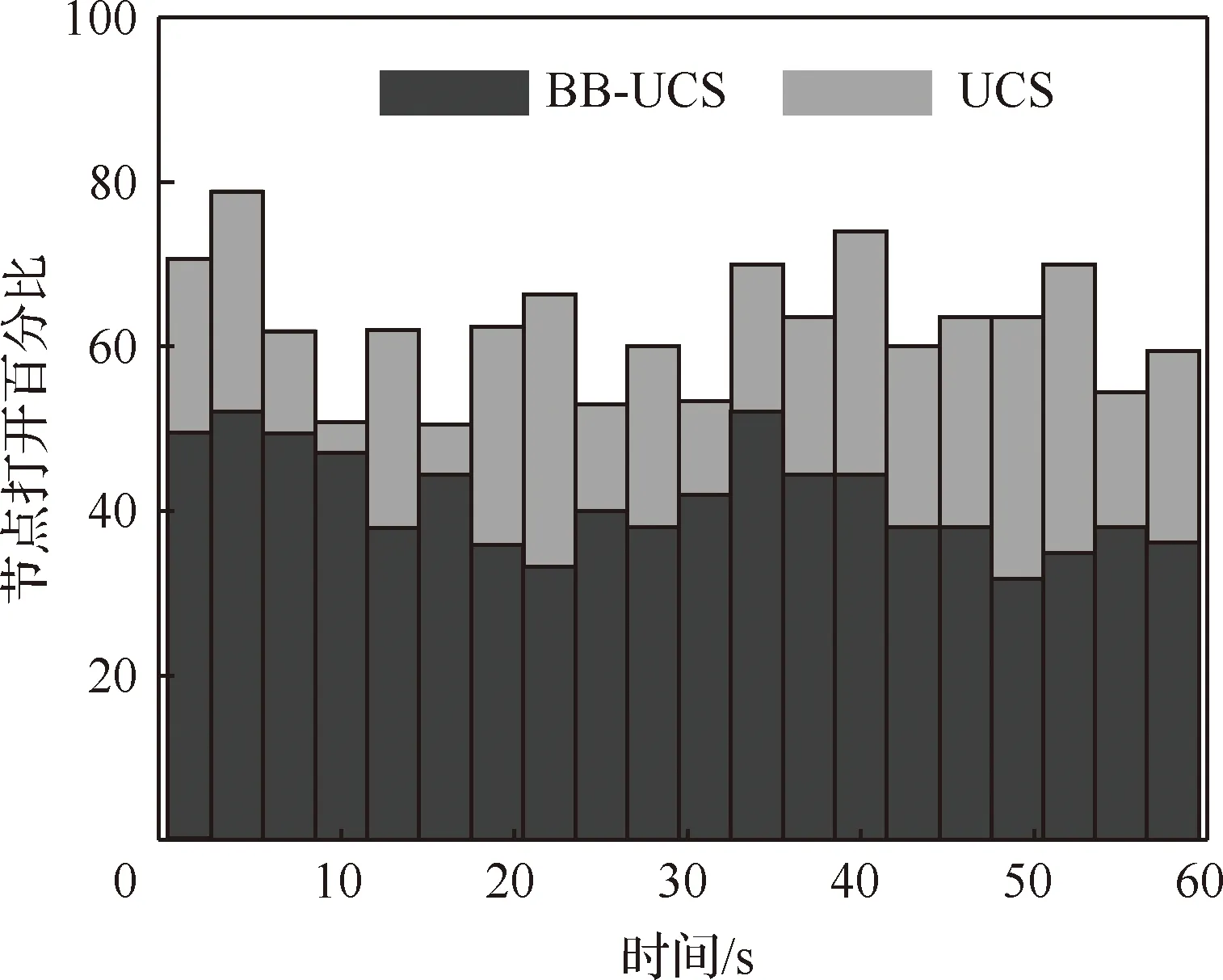
图6 不同算法下节点打开百分比Fig.6 Percentage of nodes opened under different algorithms
结合表2和图6可知,ES和UCS下的节点打开百分比和最大存储节点数较大,说明这两种算法在寻优时需要大量的时间和存储空间,实时性较差。相比之下,BB-UCS显著降低了节点打开百分比和最大存储节点,在搜索时间和内存消耗上优势明显,极大地提高了搜索效率。同时,虽然BB-UCS下的累积风险值较大,但与能获得最优解的ES和UCS的差距很小,故说明BB-UCS虽然仅能获得次优解,但依旧能够有效控制总风险以确保获得较高的作战收益。
4.3 传感器管理方法仿真
图7为总风险值随时间变化的曲线,图中,风险预测值为通过信息状态预测的未来时刻内的风险值,风险实际值为在执行分配方案后通过实际量测所计算出的风险值。可以看出在整个时间范围内,预测值与估计值大致相等,验证了本文在系统状态不可观测时利用信息状态预测未来时间内目标的运动状态和传感器的ELI状态是有效的,同时说明了以风险预测值为依据制定传感器管理方案是合理的。
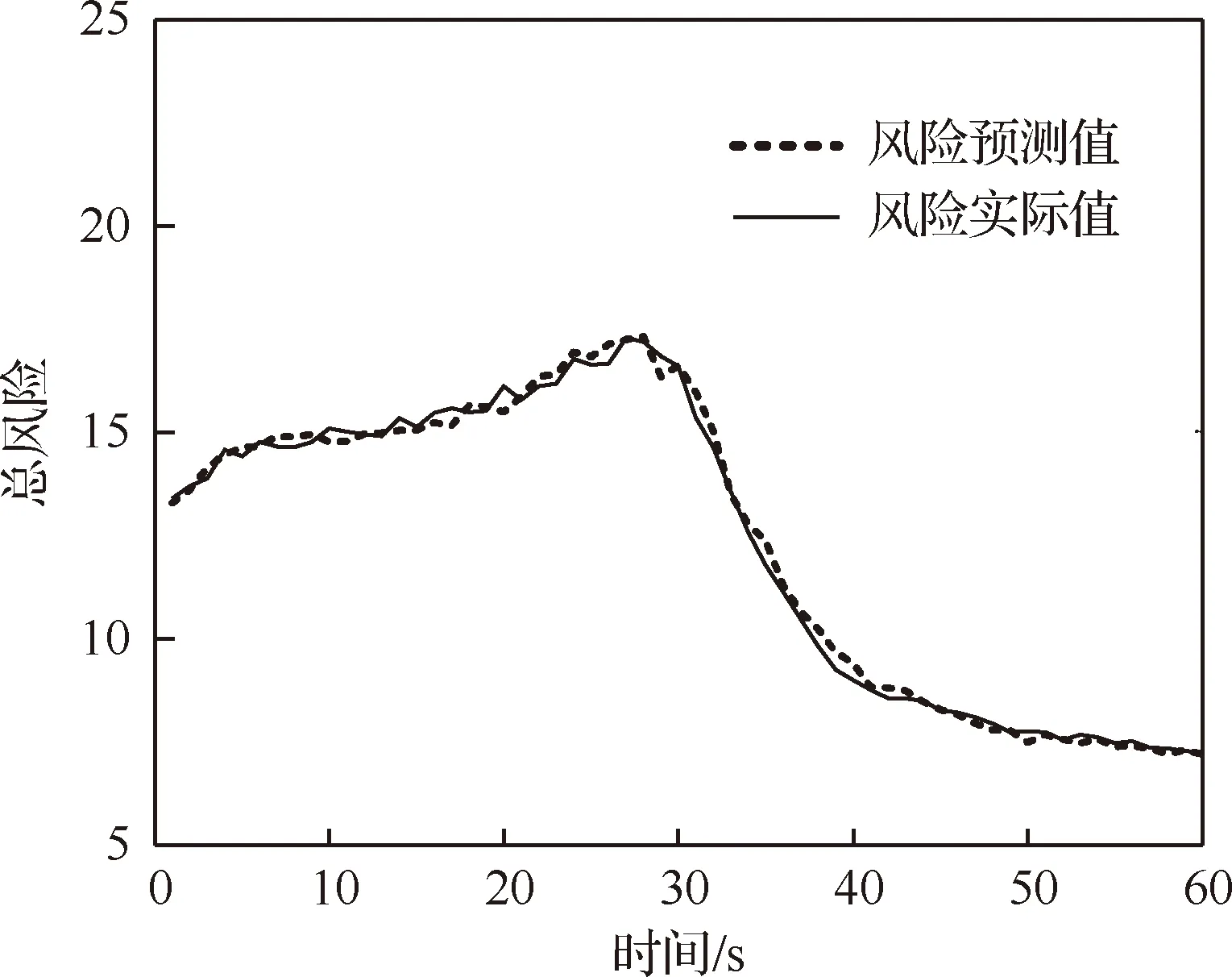
图7 总风险曲线Fig.7 Curves of total risk
图8给出了目标轨迹在x-y平面的投影和传感器的分配方案,图中目标航迹上的传感器序列代表着通过本文方法所得出的传感器最佳分配方案。图9给出了两个目标的威胁等级采样示意图。可以看出在威胁评估的过程中,目标状态的不确定性会传递到威胁度模型当中,从而在威胁等级评估时产生相应的风险。结合图7~图9可以看出,在20~30 s内,目标1和目标2的威胁度采样点在高和中两个威胁等级内均有大量分布,此时的威胁评估风险也最大,因此,图7中总风险曲线也在该时间段内逐渐上升到最大值。而在30 s后,随着目标1逐渐靠近防御中心(目标2逐渐远离防御中心),采样点的分布逐渐向高(中)威胁等级的范围内集中,落在不同区间内的采样点数量也越来越少,目标威胁评估的不确定性也随之越来越小,威胁评估风险也就越来越小,故图7中的总风险曲线也逐渐下降。在仿真时间的末段,两个目标的威胁度采样点几乎在一个威胁度区间内,此时的威胁评估风险已经非常小,影响系统决策的主要是传感器的辐射风险。当所有采样点均落在一个等级范围内时,目标威胁等级为该等级的概率为1,根据本文所提威胁评估风险计算方法可知,威胁评估风险此时为0,系统将仅需控制传感器的辐射风险。
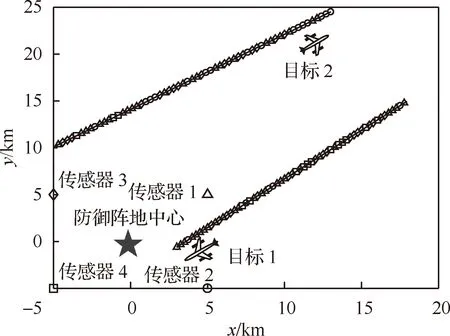
图8 目标航迹及传感器分配方案Fig.8 Target trajectory and sensor assignment scheme
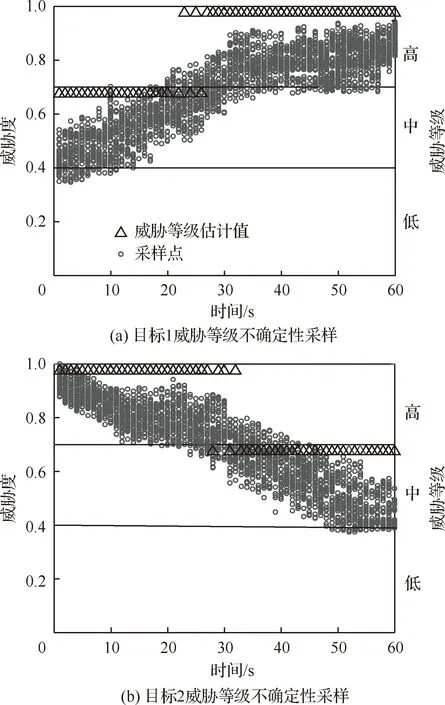
图9 威胁等级不确定性采样Fig.9 Sampling of target threat level uncertainty
为了充分说明本文所提出的管理方法(Proposed Management Approach,PMA)能够有效控制总风险,采用3种常用方法进行对比:
1) 短期管理方法(Myopic Management Approach,MMA),以一步风险预测值为依据执行传感器管理。
2) 随机管理方法(Random Management Approach,RMA)[8],每一时刻随机分配传感器评估目标的威胁等级,主要用于作战态势紧急,来不及解算目标函数的情况。
3) 最近邻管理方法(Closest Management Approach,CMA)[17],每一时刻选择与目标最近的传感器评估目标,此方法在理论上能获得较优的目标状态估计误差。
图10为不同方法下各时刻的总风险曲线对比图,图11为整个仿真时间内的累积总风险、威胁评估风险和辐射风险的对比图。可以看出,RMA不进行风险的预测,风险控制效果很差,故其3种风险均为最高;CMA在一定程度上可以保证对目标有较好的量测性能,故其威胁评估风险较低,但其实质上也不进行风险的预测,无法根据目标和传感器的实际情况制定管理方案,所以其总风险值和辐射风险较高,进一步说明了以风险预测值为决策依据的重要性。MMA通过预测未来一步内的风险值,相比于RMA和MMA,能够较大程度上改善风险控制效果,但相比于本文所提出的长期管理方法来说可视为一种贪婪搜索,无法得到最好的风险控制效果。而PMA通过对一定时域内的长期风险进行预测,使3类风险在整个仿真时间内的累积值均为所有方法中的最低,且在各个时刻也均能得到最低的总风险,说明本文方法能较好地权衡并降低威胁评估风险和辐射风险,从而控制总风险,既提高了威胁评估的准确性,又保障了传感器系统的生存性能。
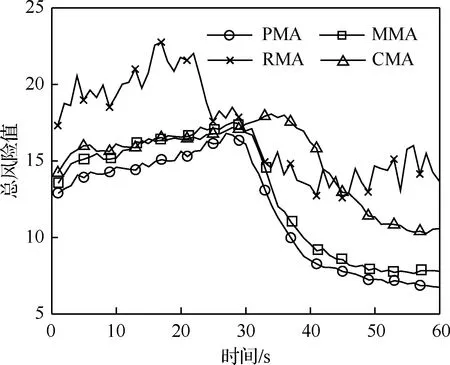
图10 不同方法下各时刻的总风险对比Fig.10 Comparison of total risk at each time under different methods
5 结 论
本文面向空中目标威胁评估任务,对多传感器管理方法进行了研究,提出了一种基于风险的传感器管理方法,主要结论如下:
1)相比于传统算法,本文所提出的基于分支定界的UCS算法能够快速搜索出质量高的解,且大大减低了搜索时间和内存消耗,保证了传感器管理的实时性要求。
2)通过与实际风险值的比较,验证了本文所提出的基于信息状态的风险预测方法能够准确预测风险值,也说明了本文以风险预测值为决策依据的思想是合理的。
3)与常用传感器管理方法相比,本文方法能有效权衡并降低威胁评估风险和辐射风险,从而提升威胁评估结果的准确性和传感器系统的战场生存能力。
