2.4 m跨声速风洞流场预测自抗扰控制
2019-12-09刘为杰何帆凌忠伟
刘为杰,何帆,凌忠伟
中国空气动力研究与发展中心 高速空气动力研究所,绵阳 621000
风洞流场的控制品质是影响风洞试验数据质量和试验效率的关键因素。风洞流场控制的主要对象是前室总压和试验段马赫数,而为了满足设备宽速域、高品质、低能耗的运行要求,大型暂冲式跨声速风洞往往设计有多种流场调节手段,因此风洞流场实际上是一个典型的多进多出系统。在跨声速条件下,气流总压和马赫数存在关联,具有强耦合性。风洞本身由于气流管路较长,具有较大的时滞特性。风洞运行过程中会受到各种扰动,上流气源的压力降低、试验过程中模型姿态改变也会引起系统控制特性的变化[1]。因此高品质的风洞流场控制技术具有一定的难度,对于更优化的流场控制方法的研究也在持续进行[2-5]。
中国空气动力研究与发展中心的2.4 m跨声速风洞(简称为2.4 m风洞)作为国内唯一的2 m量级大型跨声速风洞,是中国先进飞行器研制不可或缺的重要地面模拟试验平台。早期,该风洞流场控制系统主要采用PID控制,并且针对总压和马赫数的耦合性设计了相应的解耦器[2]。近年来,传统的PID控制已无法满足某些型号试验对风洞流场控制精度的高要求。为此,2.4 m风洞通过构建栅指、驻室流量调节阀、主排气阀以及模型攻角扰动的阶跃响应模型提出了前馈-反馈动态矩阵控制策略,提高了马赫数控制精度[3],但是仍然存在2个问题:① 针对不同的型号试验,需要重新通过试验获取攻角扰动的阶跃响应模型,增加了吹风车次;② 动态矩阵控制参数较多,且参数之间存在复杂的关联,不同参数的组合会极大地影响控制效果[6],因而给缺乏经验的设计人员带来了极大的困难和挑战。
本文旨在设计一种参数调整简单、具有较强抗扰能力的多变量控制系统,来实现2.4 m风洞试验调节阶段总压和马赫数的控制。为此,提出了自抗扰控制(Active Disturbance Rejection Control,ADRC)结合Smith预估器(Smith Predictor,SP)的控制方法,这里称为预测自抗扰控制(SPADRC)。自抗扰控制器中的扩张状态观测器(Extended State Observer,ESO)能够将总压和马赫数2个通道之间的耦合、系统的外部扰动以及系统内部参数的摄动视为总扰动估算出来,并补偿到误差反馈控制中,从而实现总压和马赫数的解耦控制,并且兼具良好的抗干扰能力。为了克服系统时滞,使用Smith预估器得到系统无时延输出并将其反馈至扩张状态观测器,加快扩张状态观测器收敛速度,从而提高控制系统的动态性能。SPADRC的研究起步较晚,至今不到10年的时间,目前在振动控制[7]、伺服控制[8]以及过程控制[9]等领域都有成功的应用。
本文主要介绍了2.4 m风洞流场模型、预测自抗扰控制原理、2.4 m风洞流场控制系统的设计与仿真,最后对全文工作进行了总结。
1 2.4 m风洞流场模型
2.4 m风洞是中国空气动力研究与发展中心的一座大尺寸空气动力试验设施,其马赫数范围为0.3~1.2,总压范围为(1.1~4.5)×105Pa。该风洞有2种典型的运转方式:① 定攻角阶梯变马赫数或定马赫数阶梯变攻角;② 连续变攻角或连续变马赫数。2.4 m风洞的运行过程分为充气启动和调节2个阶段。启动过程是指对风洞快速充压以尽快达到稳定流场。调节过程的目标则是提高流场稳态精度和抗干扰能力[10],本文研究的内容是调节过程流场控制系统设计。在调节过程中,低马赫数时(Ma≤0.85),2.4 m风洞通过主排气阀和栅指来调节总压和马赫数;高马赫数(Ma>0.85)时,该风洞则通过主排气阀和驻室流量阀来调节总压和马赫数。文献[2]给出了总压和马赫数的数学模型。
低马赫数时,模型表达式为
(1)
式中:p0为稳定段总压;Ma为试验段马赫数;u1为主排气阀行程;u2为栅指伸出量;s为Laplace算子。
高马赫数时,模型表达式为
(2)
式中:u1为主排气阀行程;u3为驻室流量阀行程。从式(1)和式(2)可以看出,低马赫数时,该系统交叉通道静态增益为0,为弱耦合系统;高马赫数时,该系统交叉通道静态增益不再为0,为强耦合系统。耦合的不利影响主要表现为:调节马赫数时会对总压造成干扰,反之亦然。耦合越强,干扰越大,这样会造成流场稳定时间变长,甚至是难以控制。此外,高马赫数时系统存在非最小相位环节,非最小相位环节对系统动态性能影响很大[11],增加了控制器设计难度。
风洞在调节过程中攻角的变化造成试验段堵塞度变化,从而会影响流场。文献[3]指出,攻角会影响静压,而对总压的影响可忽略不计,并且给出了攻角对静压的扰动模型:
1.86×10-2α2-8.06×10-4α3)
(3)
式中:Δps为静压变化量;α为攻角。而马赫数的计算表达式为
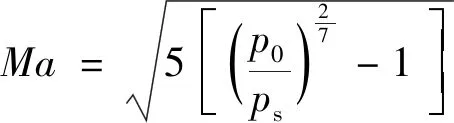
(4)
式中:ps为静压。联立式(3)和式(4)即可计算出攻角对马赫数的扰动。这里需要指出的是本文在设计SPADRC控制系统时并不需要攻角对静压的扰动模型,该模型只用于仿真分析。
2 预测自抗扰控制原理
ADRC是韩京清基于PID控制技术并吸取现代控制理论成就,提出的一种不依赖被控对象精确模型的新型控制技术[12-13]。为了减少整定参数、便于工程应用,高志强等提出了线性ADRC[14-16]。目前ADRC在许多工程领域获得了良好的控制效果[17-23]。下面简要介绍ADRC原理。
考虑一个n阶非线性、参数不确定系统:
(5)
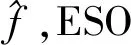
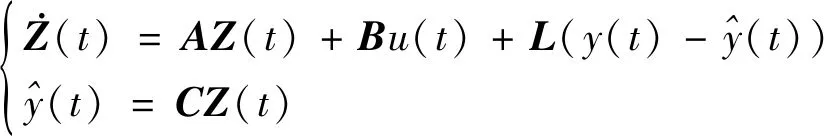
(6)
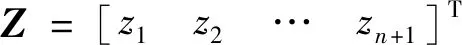

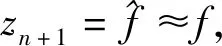
(7)
式中:u0为误差反馈控制量。将式(7)代入式(5),则原系统可转化为串联积分形式:
(8)
式(8)所表示的系统,可用如下简单的控制器律进行控制,即
u0=k1(yd-z1)-k2z2-…-knzn
(9)
式中:yd为系统输出期望值;k1,k2,…,kn为控制器的系数。文献[14]采用带宽的概念对L和k1,k2,…,kn进行整定,令ESO的带宽为ωo,控制器的带宽为ωc,则
(10)
(11)
式中:C为排列组合符号。因此,ADRC需要整定的参数有3个:b0、ωo和ωc。ADRC的结构十分简单,当系统阶数n为1时,其结构示意图如图1所示。当被控对象含有时滞环节,尤其时滞时间常数较大时,ADRC的稳定域将会减小。对于上述标准的ADRC而言,可增大b0或者减小ωo、ωc来使控制器稳定,但会牺牲系统的动态性能[24-25]。
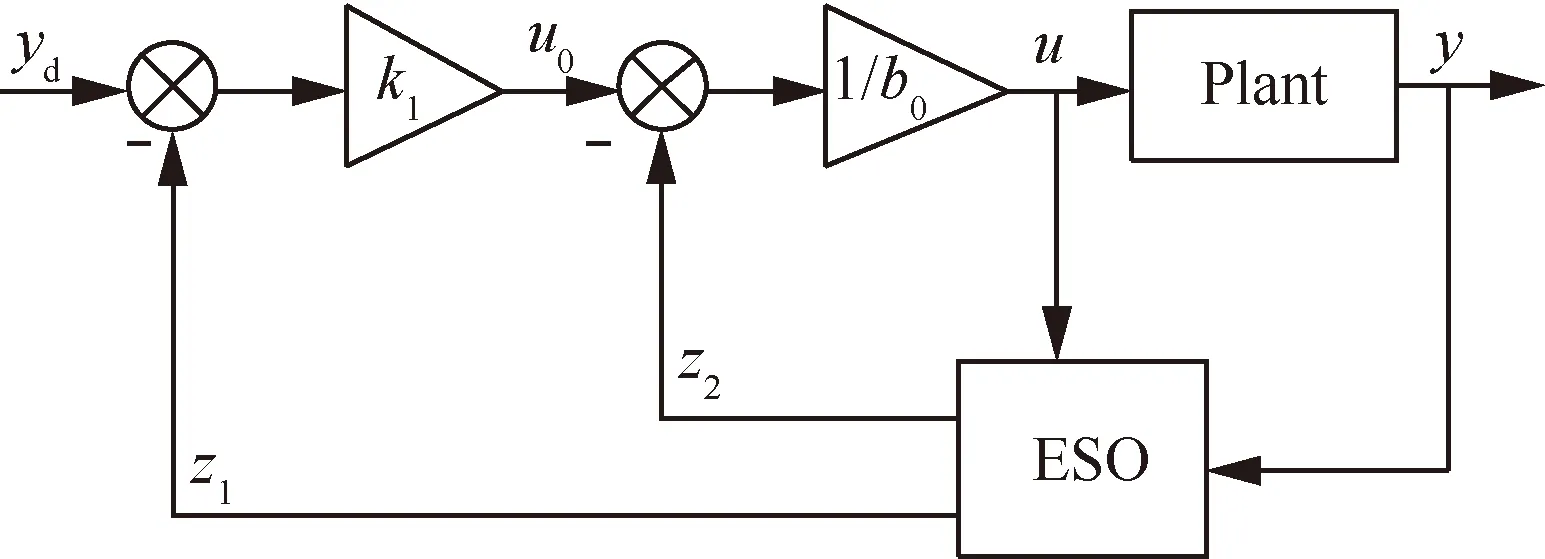
图1 ADRC结构示意图Fig.1 Structure diagram of ADRC
Smith预估器常被用于时滞系统的控制,其结构示意图见图2,通过Smith预估器可以得到系统无时延输出[26]。图2中G(s)为被控对象非时滞环节,e-τs为被控对象的时滞环节,G1(s)为被控对象非时滞环节的估计,e-τ0s为被控对象时滞环节的估计,yp为系统的预测输出。从图2中可以看出,Smith预估器的预估效果严重依赖于被控对象的精确模型,这给工程实际应用带来了一定的困难。
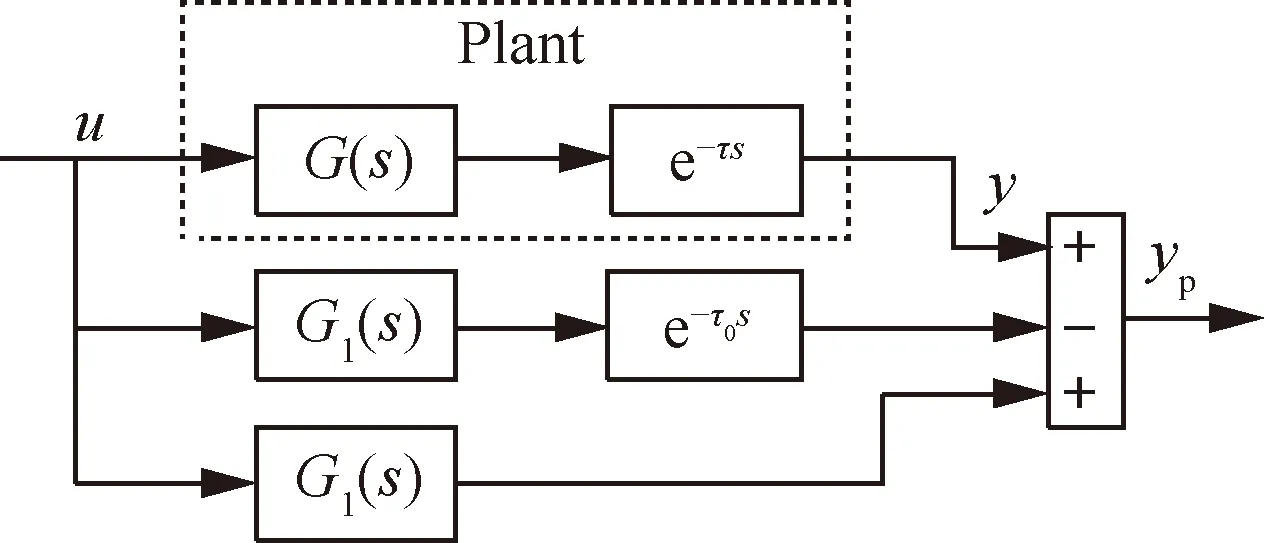
图2 Smith预估器结构示意图Fig.2 Structure diagram of Smith predictor
将Smith预估器的输出反馈至ESO中,即构成SPADRC,如图3所示。SPADRC综合了ADRC的抗干扰能力以及Smith预估器的预估能力,一方面,降低了Smith预估器对被控对象精确模型的依赖程度,另一方面削弱了时滞对ADRC的不利影响。
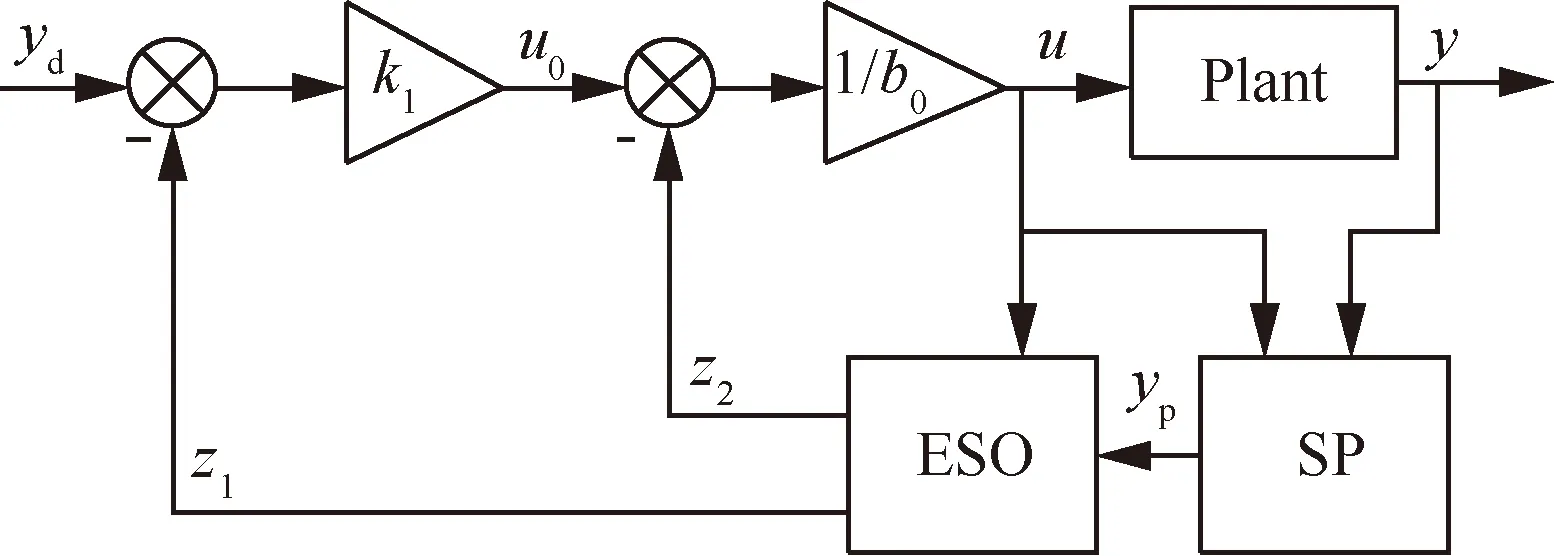
图3 一阶SPADRC结构示意图Fig.3 Structure diagram of SPADRC with first order
3 流场SPADRC控制系统设计
考虑两输入两输出(TITO)系统:
(12)
式中:u1和u2为系统输入;y1和y2为系统输出;b11、b12、b21、b22为系统参数;f1、f2为系统综合扰动。将u2对y1的影响,u1对y2的影响看成扰动,则该TITO系统可改写为
(13)
式中:f′1=f1+b12u2;f′2=f2+b21u1。设计2个分散的ESO将各自通道的扰动估计出来,然后分别在各自通道采用状态反馈进行控制,即可将TITO系统解耦成2个单输入单输出(SISO)系统。
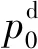
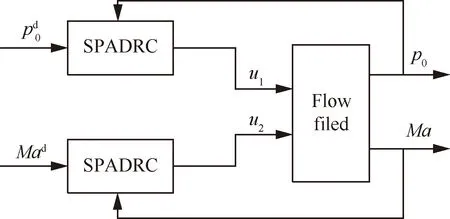
图4 流场SPADRC控制系统结构示意图Fig.4 Structure diagram of SPADRC control system for flow field
4 ESO收敛性和SPADRC抗扰特性分析
4.1 ESO收敛性分析
n取1,根据式(6)和式(10),可以计算出z1(t)和z2(t)的传递函数:
(14)
(15)
令ESO的跟踪误差e1(t)=y(t)-z1(t),e2(t)=f-z2(t),则其传递函数为
(17)
考虑典型性,y(t)和u(t)均取阶跃信号,则e1(t)和e2(t)的稳态值为
(18)
(19)
式(18)和式(19)表明: ESO具有很好的收敛性,能够实现系统状态变量和总扰动的零静差估计。
4.2 SPADRC抗扰特性分析
自抗扰控制的核心思想是通过估算并消除扰动,将被控对象近似转化为串联积分形式,转换后的被控对象越接近串联积分形式,则控制效果越好。根据式(6)、式(7)和式(10)可以推导出图3中u0至yp的传递函数为
(20)
式中:
Gp=G(s)e-τs+(1-e-τ0s)G1(s)
(21)
以式(2)中总压p0的传递函数为研究对象,并且不考虑耦合通道,即
(22)
ωo的值取7,绘制出Gu0yp的波特图如图5所示,图中Δτ和ΔTi分别表示系统时滞时间常数和惯性时间常数相对各自标称值的偏差。图5中幅频和相频响应各有6条曲线,其中黑色曲线表示采用标准的ADRC,即无Smith预估补偿时Gu0yp的幅频和相频响应曲线;其余5条曲线表示采用SPADRC,当被控对象模型中时滞时间常数和惯性时间常数存在不同偏差时Gu0yp的幅频和相频响应曲线。从图中可以看出,采用ADRC,在频率约小于1 rad/s时,可将Gu0yp近似转换成串联积分形式(传递函数为1/s);而采用SPADRC,若被控对象的模型精确已知,则在整个频段范围内都可将Gu0yp近似转换为串联积分形式,若被控对象的模型存在10%左右的偏差,则在频率小于约3 rad/s时,仍可将Gu0yp近似转换为串联积分形式。由此可见,对于时滞系统,SPADRC能够有效提高控制器的带宽,削弱了时滞带来的不利影响,同时对被控对象的建模误差具有一定的抗扰能力。
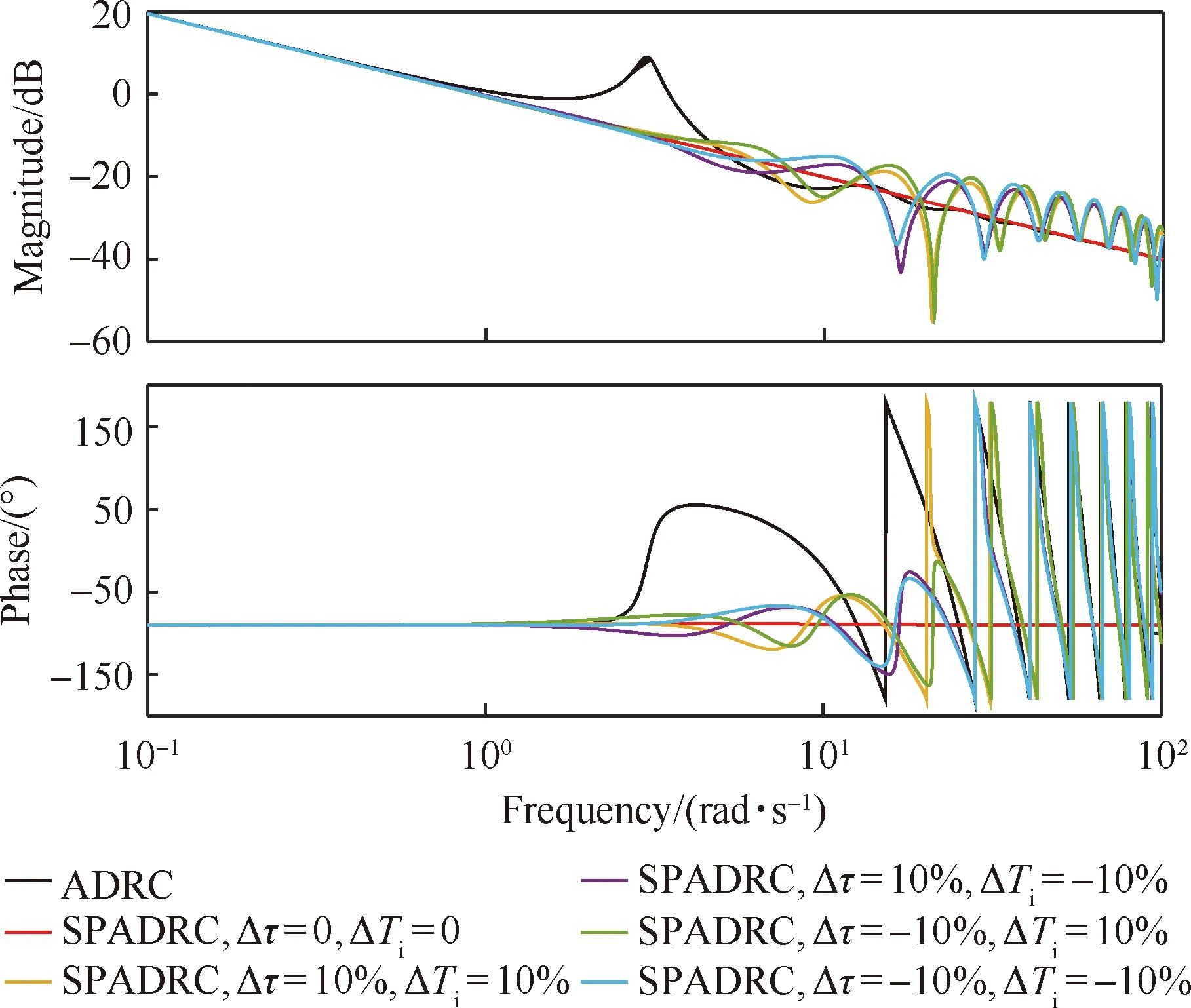
图5 传递函数波特图Fig.5 Transfer function baud diagram
5 仿真分析
在MATLAB/Simulink平台上搭建仿真模型对所提出的流场SPADRC控制系统进行仿真分析。为了与传统的流场控制方法进行对比,本文还设计了流场PI控制系统,这里对PI控制进行了改进,增加了Smith预估器以消除时滞影响。
在进行仿真之前需要设立2个前提条件:① 本文的研究内容是风洞调节过程流场的控制策略,因此假定仿真的初始时刻(0 s)风洞流场已经稳定(p0为200 kPa,Ma为0.9);② 控制系统的性能包含动态性能、稳态性能、抗干扰能力和解耦能力等多个方面,并受控制参数的影响。在对比分析2种控制算法时,需要设定一个基准,而本文选用动态性能作为基准。使用表1中的参数,使得SPADRC和PI的动态性能相接近。

表1 SPADRC和PI控制器参数Table 1 Parameters of SPADRC and PI controller
1) 设定值跟踪
t=1 s,总压设定值从200 kPa变为210 kPa,马赫数的设定值保持不变,系统的输出见图6(a);t=1 s,马赫数设定值从0.9变为1,总压设定值保持不变,系统的输出见图6(b)。从图6可以看出2种控制方法总压和马赫数的阶跃响应曲线几乎相同,但是SPADRC的解耦能力明显优于PI。
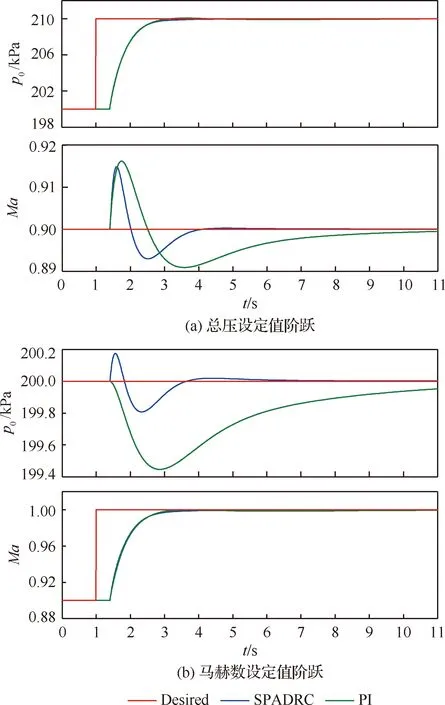
图6 阶跃响应曲线Fig.6 Step response curves
2) 连续变马赫数
保持总压设定值不变,马赫数设定值从0.9~1.2连续变化,变化率为0.25 s-1,系统输出见图7。可见,SPADRC和PI马赫数跟踪性能相同。而采用PI控制时,总压波动达到0.5 kPa;采用SPADRC时,总压波动小于0.1 kPa,进一步表明SPADRC较PI具有优良的解耦能力。
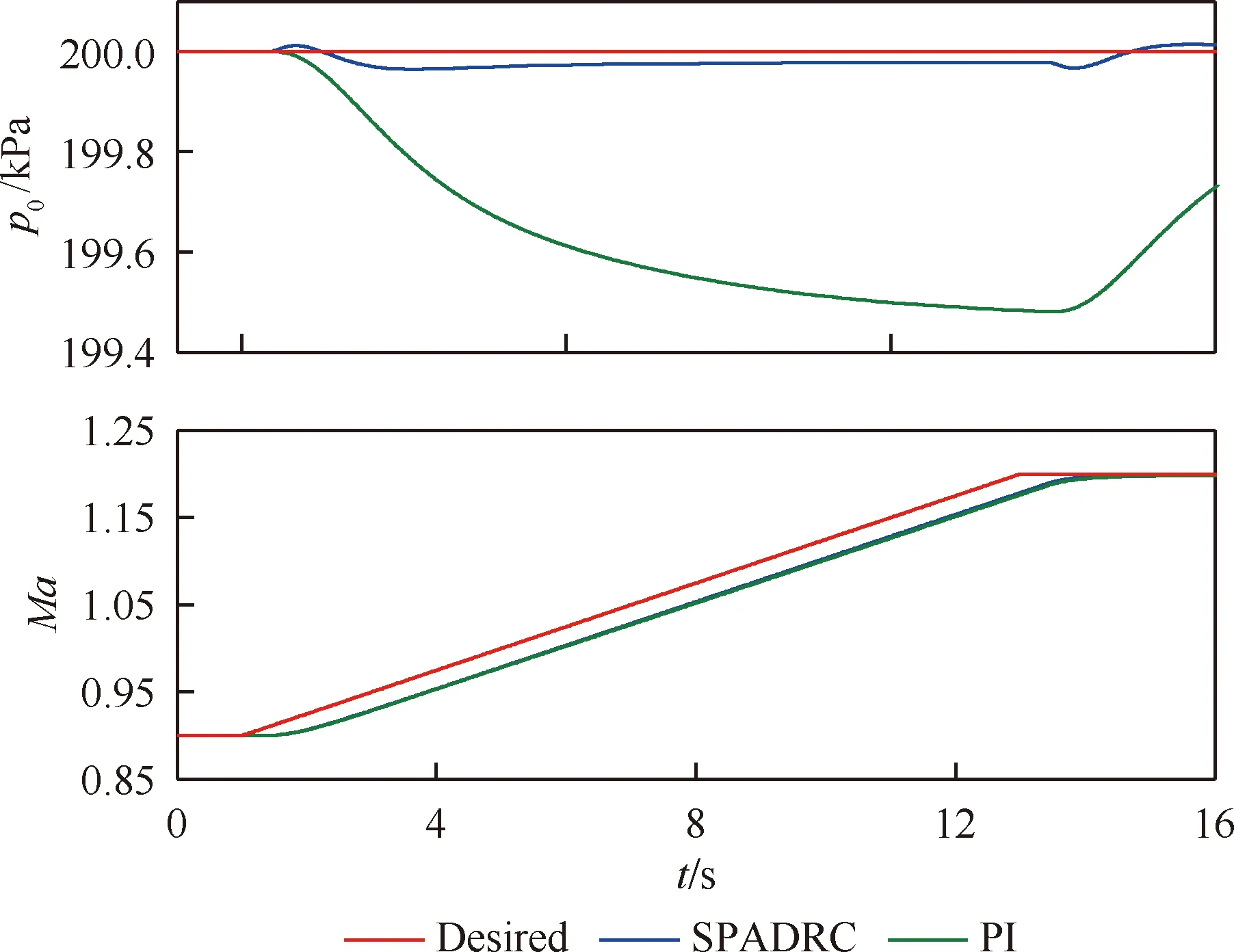
图7 连续变马赫数时系统输出曲线Fig.7 System output curves when Mach number changes continuously
3) 阶梯变马赫数
保持总压设定值不变,马赫数设定值从0.9~1.2阶梯变化,阶梯值为0.1,间隔时间为4 s,系统输出见图8。与图7类似,SPADRC和PI马赫数跟踪性能相同。而采用PI控制时,总压波动约为0.7 kPa;采用SPADRC时,总压波动小于0.2 kPa,同样证明了SPADRC优良的解耦能力。
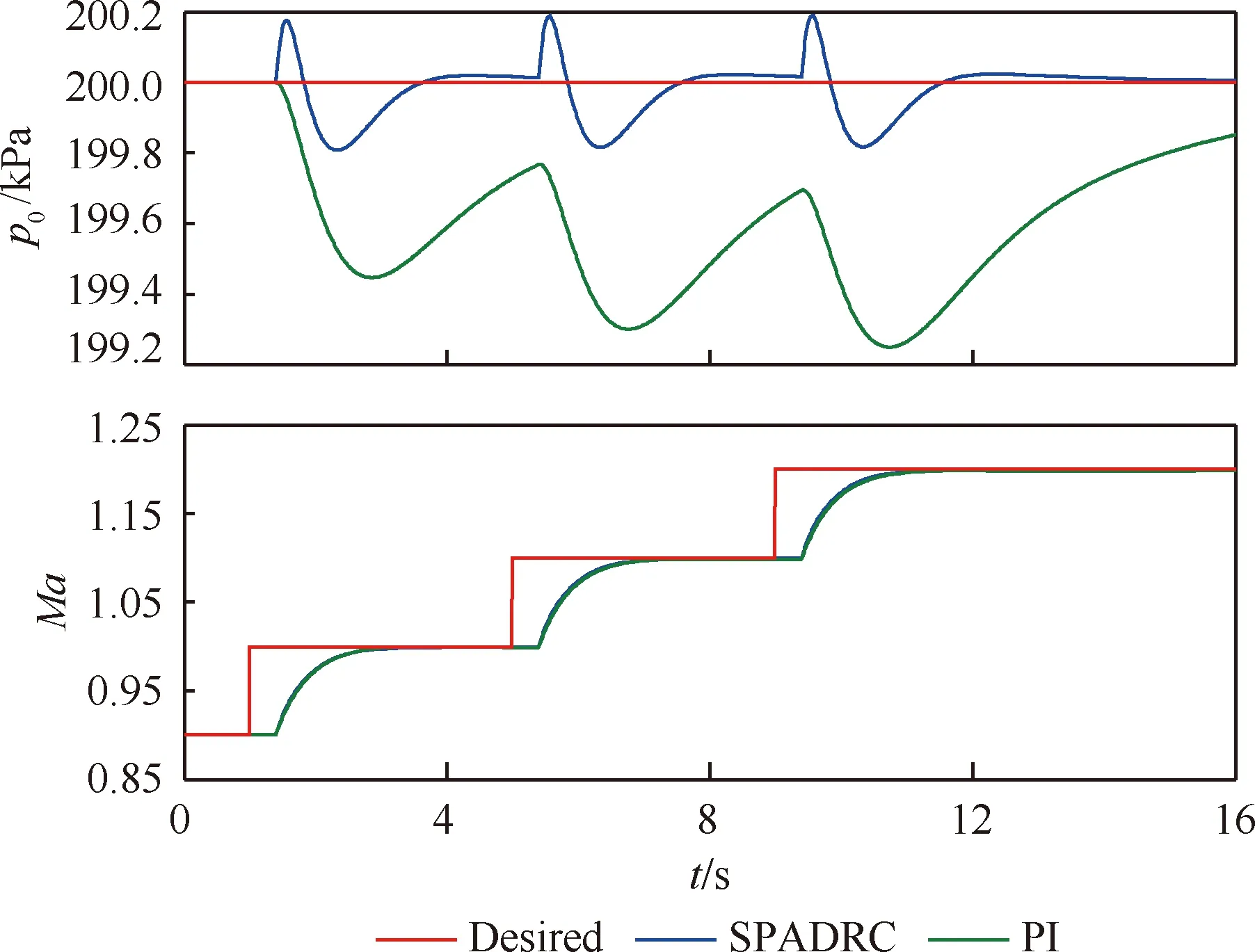
图8 阶梯变马赫数时系统输出曲线Fig.8 System output curves when Mach number changes by step way
4) 连续变攻角
保持马赫数的设定值不变,攻角α从-10°~20°连续变化,变化率为2 (°)/s,马赫数变化见图9。SPADRC对应的马赫数波动约为0.002,PI对应的马赫数波动约为0.007,表明SPADRC的抗干扰能力明显优于PI。
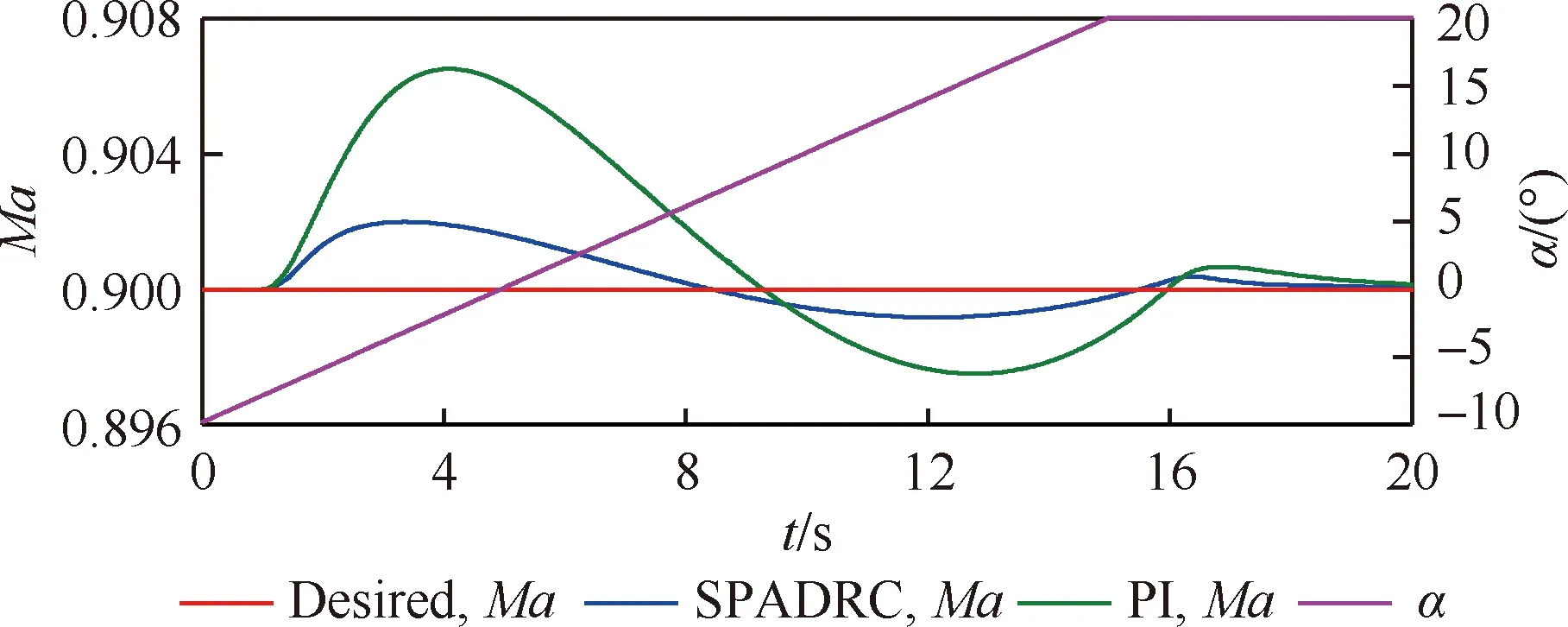
图9 连续变攻角时马赫数曲线Fig.9 Curves of Mach number when angle of attack changes continuously
5) 阶梯变攻角
保持马赫数的设定值不变,攻角从-10°~20°阶梯变化,阶梯值为2°,间隔时间为1 s,马赫数变化见图10。类似地,SPADRC对应的马赫数波动约为0.002,PI对应的马赫数波动约为0.007,同样证明了SPADRC的抗干扰能力明显优于PI。
6) 鲁棒性测试试验
将被控对象的时滞时间和惯性时间常数在各自标称值的基础上分别提高10%和降低10%,组合成4种情形,记录SPADRC输出曲线,并与标称值下SPADRC和PI输出曲线进行对比,如图11所示。可以看出在系统参数摄动时,SPADRC阶跃响应曲线基本保持不变,解耦能力略有变化,但是仍远优于PI,SPADRC表现出优良的鲁棒性。
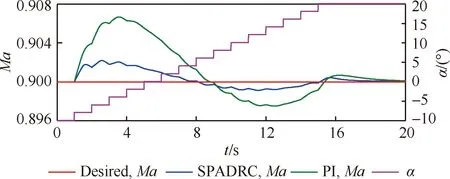
图10 阶梯变攻角时马赫数曲线Fig.10 Curves of Mach number when angle of attack changes by step way
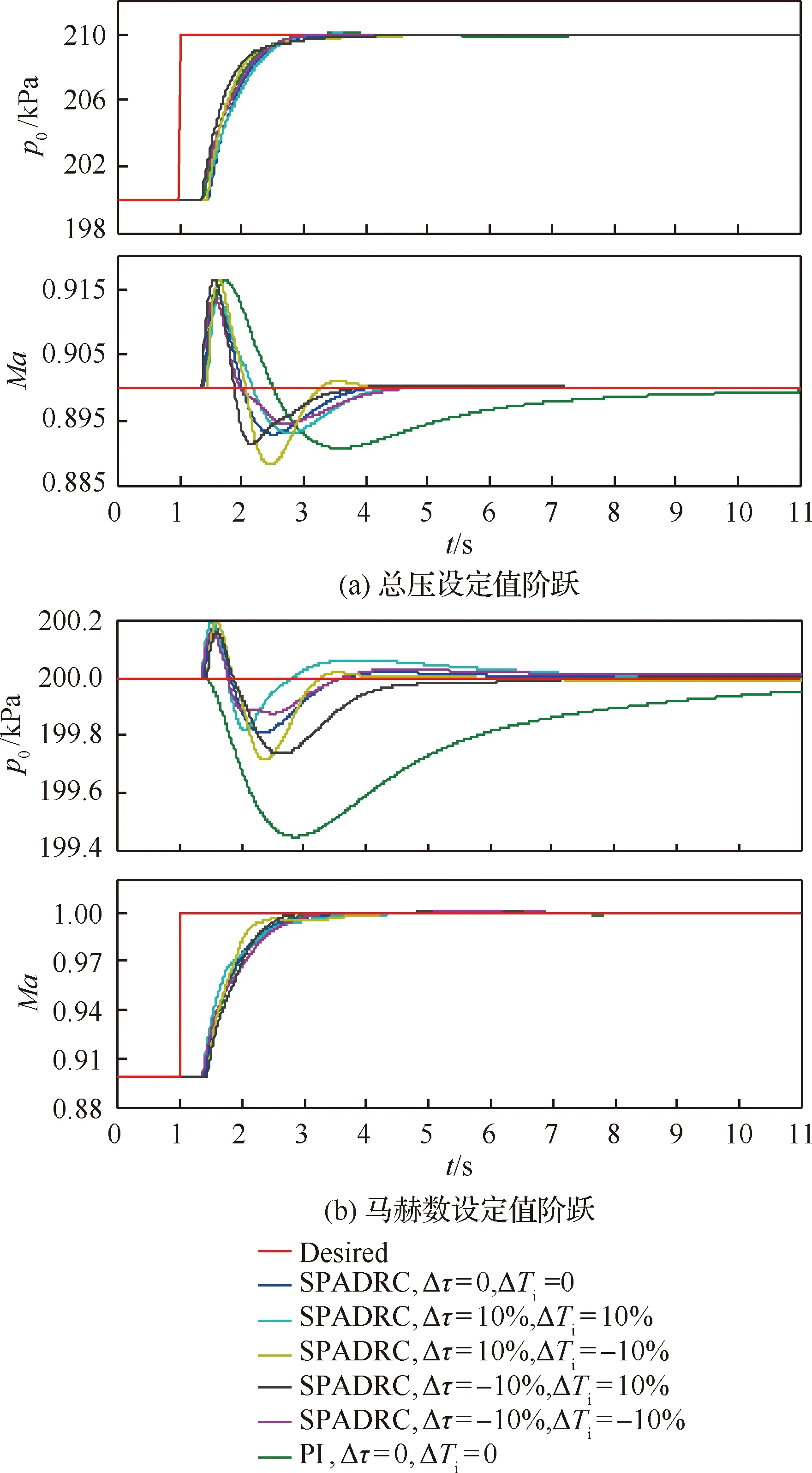
图11 鲁棒性测试系统输出曲线Fig.11 System output curves of robust test
6 结 论
1) 本文将SPADRC控制方法引入2.4 m风洞流场控制系统中,该方法无需额外设计解耦器,通过ESO将总压和马赫数2个通道之间的耦合以及其他扰动估计出来并补偿到误差反馈控制中,即可实现总压和马赫数的解耦控制。
2) 仿真研究中,对总压和马赫数2个回路分别做了设定值跟踪试验和鲁棒性能试验,并对2.4 m风洞2种典型的运行方式进行仿真,同时与PI控制器作了对比。结果表明SPADRC具有良好的解耦能力、抗干扰能力,鲁棒性强,不依赖系统精确模型,参数整定简单方便。
本文后续将在2.4 m风洞开展SPADRC流场控制算法试验研究,对该控制方法的性能进行进一步验证。
