HCKF性能评估及其在传递对准中的应用

苏炳志，穆荣军，龙 腾，程 超，崔乃刚

(1. 哈尔滨工业大学航天学院，哈尔滨 150001；2. 北京机电工程研究所，北京 100074)

0 引 言

传递对准是指在自然扰动或战术机动的动态环境下，利用已处于导航状态的高精度主惯导系统对子惯导系统进行初始对准的一种方法。1989年美国学者Kain等首次提出基于“速度+姿态”匹配的快速传递对准方法[1]，提高了对准收敛速度和减小了对运动平台的机动要求，在快速响应的舰载机和舰载武器系统中得到广泛的应用。舰载机着陆在舰船甲板上的位置是任意的，而舰船主惯导系统却安装在甲板下方的导航室内；此时，主子惯导之间的失准角可能很大，需要建立大失准角传递对准模型[2-3]。

基于贝叶斯框架的非线性滤波和估计为大失准角传递对准系统提供了最优的解决方案，特别是利用不同采样策略对非线性高斯系统状态的后验均值和方差进行近似的高斯滤波。其中，UKF(Unscented Kalman filter)通过使用一组sigma点经非线性函数传递后的加权和来逼近状态的概率密度函数，但只有3阶精度[4-6]；为了提高估计精度，Arasaratnam等[7]基于高斯厄米特积分(Gaussian-Hermite quadrature,GHQ)提出了GHQF(Gaussian-Hermite quadrature filter)，能够达到任意阶的估计精度，但由于多维GHQF是由单维GHQ准则通过张量积直接扩展得到的，因此GHQF的积分点随着状态维数的增加呈指数增长，即“维数灾难”；针对高维状态估计，Arasaratnam等[8]基于3阶球面-径向容积准则，提出了容积卡尔曼滤波(Cubature Kalman filter, CKF)，文献[9-10]基于Genz积分和矩匹配法推导了任意阶的球面积分和径向积分，从而建立了高阶容积卡尔曼滤波。HCKF(High-degree cubature Kalman filter)作为一种新兴的滤波算法被运用于对准系统中[11-12]。

针对非线性滤波算法的性能评估，国内外学者的研究重点主要在滤波估计精度分析[13-16]，较少有分析算法计算量的。运用泰勒级数展开精度分析法：文献[13-14]分析了UKF算法的估计精度，文献[15]比较分析了UKF和CKF的估计精度，文献[16]对UKF、CKF和GHQF三种滤波算法的精度进行了比较分析。文献[17]运用计算复杂度分析了传递对准滤波器的计算量，但仅适用于标准卡尔曼滤波。

本文以舰机大失准角传递对准为应用背景，建立非线性快速传递对准模型；基于高阶球面-径向容积准则建立HCKF算法模型；综合运用多变量函数泰勒级数展开和计算复杂度分析对HCKF的估计精度和计算量予以分析，并与GHQF和UKF进行比较，综合评估滤波算法性能；参照GHQF和UKF，分别通过舰机大失准角传递对准摇摆台试验中的对准精度统计和计算耗时加以验证，从而综合验证HCKF性能评估方法的有效性。

1 非线性快速传递对准模型

1.1 捷联式惯导系统误差传播模型

以“北-天-东”地理系为导航系，大失准角下的非线性快速传递对准误差模型为[1,18]：

(1)

(2)

(3)

1.2 非线性快速传递对准模型

考虑到对准时间短，对陀螺仪零偏和加速度计零偏没有估计效果，且高精度的器件误差对对准精度影响小，为了减小计算量，提高运行速度，因此未将其列入传递对准状态向量中；鉴于本文的研究重点是进行HCKF算法的性能评估，而非挠曲变形建模，因此在初始对准过程中，认为主、子惯导之间的位置是固定不变的。根据式(1)，构建9维非线性快速传递对准模型，采用“速度+姿态”匹配实现舰机之间的快速传递对准。

1.2.1非线性快速传递对准状态模型

选择量测失准角矢量ψm，速度误差矢量δV和安装偏差角矢量ψa为传递对准状态向量，即：

(4)

根据式(1)可得到状态模型微分方程：

(5)

1.2.2非线性快速传递对准量测模型

选择速度误差矢量δV和量测失准角矢量ψm为传递对准量测向量，即：

(6)

式中：Vm,Vs分别为主惯导和子惯导的速度矢量，g(·)表示从方向余弦矩阵求取欧拉角的函数，矩阵Cz的定义如下：

(7)

式(6)中：

2 高阶容积卡尔曼滤波算法

2.1 高阶球面-径向容积准则

考虑如下非线性离散系统状态空间模型：

(8)

其中，xk∈Rn是状态向量，zk∈Rm是量测向量，f(·)和h(·)是非线性向量函数，可分别由非线性快速传递对准状态模型和量测模型求得，wk-1和vk分别为过程和量测噪声，均方误差矩阵分别为Qk-1和Rk。

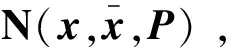
(9)

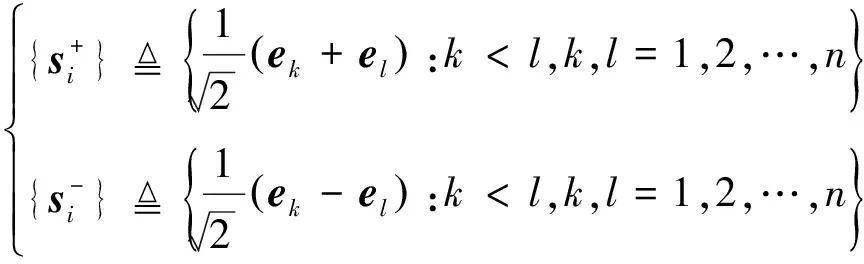
(10)

2.2 高阶容积卡尔曼滤波算法

根据式(8)和(9)并结合非线性高斯滤波递推公式[8]可得到高阶(5阶)容积卡尔曼滤波的具体计算步骤：

1) 时间更新

计算k-1时刻的容积点

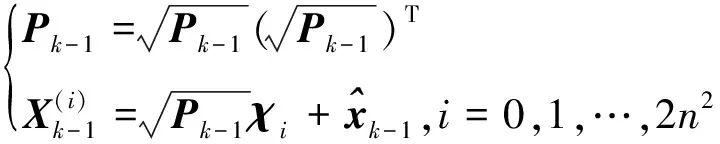
(11)

其中，n是状态向量维数，向量为：

χi=

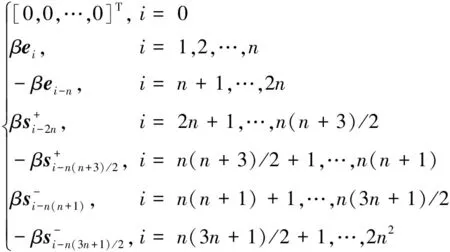
(12)

一步预测：

(13)

式中权值wi为：

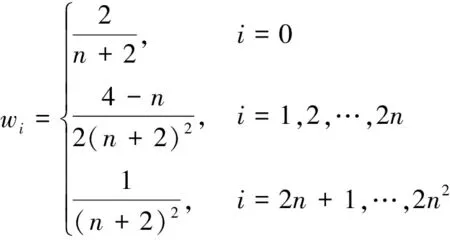
(14)

2) 量测更新

计算量测更新容积点：

(15)

经量测非线性变换的容积点：

(16)

计算滤波增益：

(17)

状态估计值及协方差阵计算：

(18)

3 高阶容积卡尔曼滤波算法性能评估

性能评估由算法的估计精度和计算量分析两部分组成。分别以滤波算法的泰勒级数展开精度和计算复杂度评估HCKF估计精度和计算量，并与GHQF和UKF进行比较。

3.1 高阶容积卡尔曼滤波算法精度分析

3.1.1多变量函数泰勒级数展开

(19)

3.1.2高阶容积卡尔曼滤波估计精度

(20)

其中，

δxi=

(21)

根据式(19)，并考虑到2n2+1个HCKF算法的容积点是对称的，奇数阶矩相互抵消，则映射后f(x)的均值为：

(22)

其中，二阶矩计算过程为：

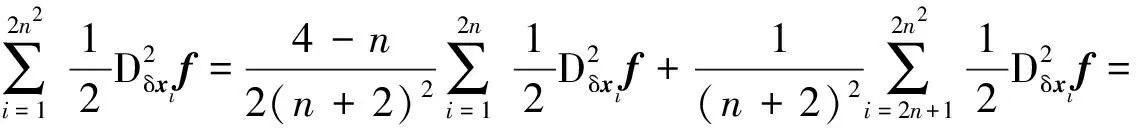
(23)

若考虑其他偶数阶泰勒级数展开项，i=1,2,…,2n时

(24)

同理，i=2n+1,2n+2,…,2n2时

(25)

根据式(24)和(25)可得：

(26)

由式(23)和(26)可得：

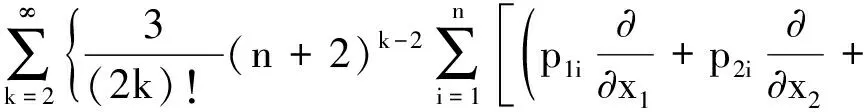
(27)

3.1.3GHQF和UKF估计精度

(28)

(29)

3.1.4估计精度比较

将式(27)～(29)分别与多变量函数泰勒级数展开式(19)比较可知，高阶(5阶)容积卡尔曼滤波能精确传播至5阶项，从6阶项开始出现截断误差，即有5阶泰勒级数展开精度；GHQF的估计精度由单维高斯厄米特积分点数q决定，qn个积分点的多维高斯厄米特积分滤波能够精确传播至2q-1阶项，从2q阶项开始出现截断误差。UKF能精确传播至3阶项，从4阶项开始出现截断误差，即有3阶泰勒级数展开精度。

3.2 高阶容积卡尔曼滤波计算量分析

对于一种滤波算法不仅需要考虑它的估计精度，而且还必须考虑它的计算量。本节将建立计算复杂度模型来评估HCKF算法的计算量，并与GHQF和UKF进行比较分析。

3.2.1三种滤波采样点数

HCKF、GHQF和UKF均属于确定性采样滤波方法[19]，下面将容积点、积分点和sigma点统称为采样点，三种滤波算法的采样点数与状态向量维数n的关系如式(30)和表1所示：

(30)

其中，为了更好地比较分析HCKF算法的性能，GHQF的估计精度也取5阶，即q=3。

表1 HCKF、GHQF和UKF采样点数Table 1 Number of sampling points for HCKF,GHQF and UKF

3.2.2计算复杂度建模

求取k-1时刻容积点式(11)的计算复杂度

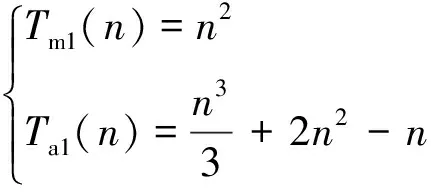
(31)

式中：Tm1(n)表示乘法个数，Ta1(n)表示加法个数，Cholesky分解(平方根法)的计算复杂度n3/3按加法计算。

一步预测式(13)的计算复杂度

(32)

式中：Mx和Ax分别表示非线性传递函数f(x)的乘法和加法运算个数，Nm为采样点数。

求取量测更新容积点式(15)的计算复杂度

(33)

求取经量测非线性变换容积点式(16)的计算复杂度

(34)

式中：Mz和Az分别表示非线性量测函数h(x)的乘法和加法运算个数。

滤波增益计算式(17)的计算复杂度

(35)

状态估计及方差矩阵更新式(18)的计算复杂度

(36)

由式(31)～(36)，算法的计算复杂度T(n)为：

(n2+nm+m2+n+3m)Nm+

(Mx+Mz)Nm+n2m+2n2+2nm2+nm

(37)

(n2+nm+m2+4n+4m)Nm+

(Ax+Az)Nm+m3+2/3n3+n2m+

nm2+5n2+m2-3nm-2n

(38)

T(n)=Tm(n)+Ta(m)

(39)

式中：Tm(n)表示乘法个数，Ta(n)表示加法个数，T(n)表示算法的计算复杂度。

3.2.3算法计算量分析

量测向量维数m一般小于状态向量维数n，因此HCKF的计算复杂度与状态维数n的四次方成正相关，即T(n)=O(n4)；而GHQF的计算复杂度随着状态维数n的增加呈指数增长趋势，即T(n)=O(n2×3n)[20]；UKF的计算复杂度与状态维数n的三次方成正相关，即T(n)=O(n3)[20]。

由于计算复杂度越大，算法的计算量越大，因此根据上述理论分析可知，在相同精度等级条件下HCKF的计算量比GHQF小。

3.3 性能评估在大失准角传递对准中的应用

将基于多变量函数泰勒级数展开和计算复杂度分析的性能评估方法运用到大失准角传递对准中。

根据第3.1.4节估计精度比较可知，HCKF与GHQF都具有5阶泰勒级数展开精度，高于UKF的3阶泰勒级数展开精度，在舰机大失准角传递对准等强非线性系统中更加能突显HCKF的精度优势。根据第3.2.3节算法计算量分析可知，对于大失准角传递对准模型(n=9)，此时HCKF的计算量比UKF的高1个数量级，但比GHQF的小2个数量级。

综合上述分析，HCKF能够有效提高舰机大失准角传递对准精度，同时又不会致使计算量急剧增大，综合性能更优，更加有望运用于工程实际中。

4 试验校验

为了校验高阶(5阶)容积卡尔曼滤波性能评估的理论分析结果，开展了快速传递对准摇摆台试验。为了尽量排除干扰，在相对比较理想的试验条件下进行试验验证，能更加精准的评估HCKF算法性能，因此试验主子惯导之间是刚性连接的。利用六自由度摇摆台模拟中等海况[3]：载体的俯仰角ϑ，横滚角γ，偏航角ψ的幅值和周期分别为5°和8 s，横荡、纵荡和垂荡引起的线速度幅值和周期分别为0.1 m和10 s。摇摆台试验系统组成及主子惯导器件指标如图1所示。

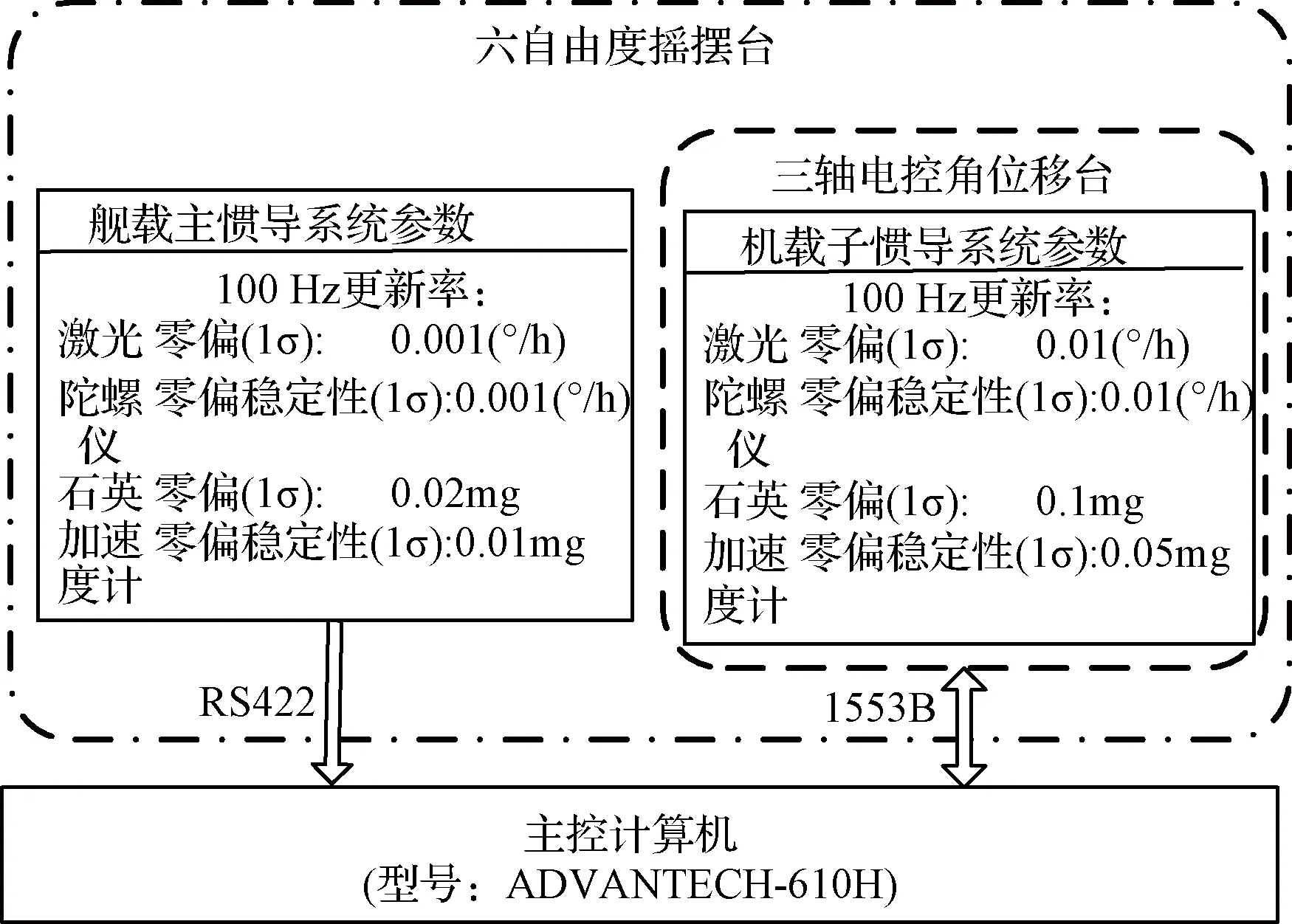
图1 快速传递对准摇摆台试验系统结构Fig.1 The rapid transfer alignment swing bench test system

为了全面考核与验证算法对安装偏差角估计的正确性，通过三轴电控角位移台改变主子惯导之间的安装偏差角，水平安装偏差角ψax=3°，ψaz=3°，航向安装偏差角可取ψay=±10°,±20°, ±30°,±40°,±50°，共10个试验工况。

基于三种非线性滤波算法的快速传递对准摇摆台试验安装偏差角估计误差曲线(航向安装偏差角20°工况)如图2～图4所示，10次摇摆台试验对准精度统计结果(安装偏差角估计值与光学瞄准获得的真值相比)如表2所示，三种滤波算法单次计算耗时(硬件配置：Core i7-4790 CPU，软件配置：Visual Studio 2005)如表3所示。

图3 Y轴安装偏差角估计误差Fig.3 Estimation error of installation deviation angle of Y axis

图4 Z轴安装偏差角估计误差Fig.4 Estimation error of installation deviation angle of Z axis

由图2～4和表2～3三种滤波算法在传递对准中的试验结果可知，从对准精度角度分析HCKF和GHQF的估计精度相当，比UKF高17%。从计算耗时角度分析，HCKF单次计算耗时为0.187 ms稍高于UKF的0.024 ms，但比GHQF的23.83 ms小2个数量级；UKF和HCKF计算耗时小于惯导的更新周期(10 ms)，而GHQF的计算耗时大于惯导的更新周期，不能满足实时计算需求。HCKF在有效提高对准精度的同时又能保证系统的实时性，综合性能更优，具有更加广阔的运用前景；传递对准精度统计和计算耗时结果与HCKF算法精度和计算量分析结果一致，校验了基于多变量函数泰勒级数展开和计算复杂度分析的性能评估方法的有效性。

表2 10次传递对准试验RMSE统计结果Table 2 Statistics results of transfer alignmentRMSE in 10 tests

表3 三种滤波算法计算耗时比较Table 3 Comparison of filtering computation times

5 结 论

本文以舰机大失准角传递对准为应用背景，建立了非线性快速传递对准模型；基于高阶球面-径向容积准则建立了HCKF算法模型，利用多变量泰勒级数展开和计算复杂度分析衡量HCKF的估计精度和计算量，从而综合评估HCKF的性能，并与GHQF和UKF进行比较。理论分析表明：HCKF和GHQF均具有5阶泰勒级数展开精度，高于UKF的3阶精度；HCKF的计算复杂度O(n4)比UKF的O(n3)高一个数量级(n=9)，但比GHQF的O(n2×3n)小2个数量级。舰机大失准角传递对准摇摆台试验校验表明：HCKF的估计精度与GHQF相当，比UKF高17%，计算量稍高于UKF，但比GHQF小2个数量级，满足实时计算需求；HCKF能够兼顾估计精度与计算量，综合性能更优，运用前景更加广阔；试验结果与HCKF的性能评估理论分析结果一致，校验了性能评估算法的有效性。