柔性航天器姿态机动轨迹设计及跟踪控制

张秀云，宗 群，朱婉婉，刘文静

(1. 天津大学电气自动化与信息工程学院，天津 370002；2. 北京控制工程研究所，北京 100190)

0 引 言

近年来，随着航天科技的飞速发展，一方面为降低发射成本，现代航天器广泛采用轻质柔性附件；另一方面随着航天需求的不断增加，航天器在轨时间要求越来越长，因此柔性太阳帆板等尺寸逐渐增大。在航天器完成大角度机动动作时，若机动速度过快，则会导致剧烈的柔性振动，影响系统稳定性；但若机动速度过慢，则不能满足机动快速性需求。因此，柔性航天器姿态机动存在“快速性”及“稳定性”的矛盾，如何保证既快又稳的姿态机动、并有效抑制柔性振动是目前研究的热点及难点问题。

为进行航天器姿态机动，快速有效的完成航天任务，首先需要设计姿态机动轨迹，若不对轨迹进行规划，直接由初始点机动至终止点，可能会难以满足机动时间要求，且带来极大的柔性振动。文献[1]针对柔性航天器姿态机动问题，利用控制力矩分配的优化策略设计了一种新型机动曲线，但其仅考虑了机动快速性，未考虑系统稳定性。文献[2]通过傅里叶分析Bang-Coast-Bang(BCB)路径谱以确定柔性航天器姿态机动轨迹，但其仅单纯考虑了系统稳定性。以上文献在姿态机动轨迹设计过程中，均单一考虑了机动的“快速性”或“稳定性”，未进行两者的综合考虑。

针对柔性航天器主动振动抑制问题，国内外学者进行了大量研究。输入成形器(Input shaper，IS)是一种有效抑制振动的前馈控制方法，得到了广泛的应用[3]。输入成形器是指具有一定作用幅值及作用时间的脉冲序列，利用合适的输入成形器与系统参考指令相卷积，改变系统输入的形状和作用位置点，达到抑制振动的目的[4]。近年来，输入成形器发展了多种形式[5]：Zero-Vibration(ZV)，Zero Vibration and Derivative (ZVD)，Extra-Insensitive (EI)等，但在作用时间及鲁棒性方面仍然是难点问题。

针对柔性航天器姿态控制问题[6]，输入成形器与控制方法的结合也被广泛应用[7-8]。文献[9-10]利用输入成形解决大型航天器柔性附件振动问题，取得了很好的抑制效果。文献[11-12]通过结合输入成形器及滑模控制方法，解决了干扰影响下的柔性航天器控制，但其仅能保证姿态的渐近收敛。为避免控制器设计过程中必须不确定上界已知的限制，自适应算法被广泛应用于滑模控制中[13-16]，如何设计能够避免增益过估计、且能保证跟踪误差有限时间收敛到零的自适应滑模控制器是研究的重点问题。

在上述研究基础上，本文针对柔性航天器大角度姿态机动问题，采用优化与控制综合方法，综合考虑机动快速性及稳定性，优化得到姿态机动轨迹，并设计新型输入成形器-无过估计的自适应有限时间控制器，有效减小输入成形器作用时间，抑制柔性振动，实现对优化轨迹的快速高精度跟踪控制。

1 航天器姿态模型建立

采用单位四元数描述航天器姿态，则航天器运动学模型描述为[17]：

(1)

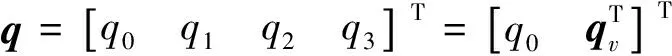
刚柔耦合航天器姿态动力学方程及柔性振动方程可描述为：

(2)

根据文献[18-19]，在柔性帆板的表面附着轻薄且均匀的压电致动器，其产生的压电输入up作用于柔性帆板，会改变柔性动力学方程：

(3)

式中：δ2为耦合矩阵，up将由输入成形器进行设计，从而保证加入up后所产生的系统振动响应能够相互抵消，从而达到抑制振动的效果。

(4)

(5)

(6)

其中，R为期望坐标系至本体坐标系的旋转矩阵：

(7)

由式(6)可以看出，若姿态机动速度过快，则会导致剧烈的柔性振动，进而严重影响系统的稳定性；但机动速度过慢，则不能满足任务需求，因此，姿态机动存在“快速性”与“稳定性”的矛盾。

本文所采用的控制策略如图1所示，主要包括姿态机动轨迹设计、输入成形器及自适应连续滑模控制器三部分，后续将进行详细介绍。

图1 综合控制策略设计框图Fig.1 Block of integrated control strategy

2 姿态机动优化轨迹设计

针对姿态机动过程中快与稳的矛盾，本节通过建立多目标多约束问题，利用高斯伪谱法求解，设计满足机动快速性基础上、最大限度降低柔性振动的姿态机动轨迹。

2.1 多目标多约束条件建立

卫星姿态机动轨迹优化的约束条件主要包括边值约束及路径约束，具体描述如下：

边值约束为卫星姿态机动的初始状态和末端状态，本文设定的机动任务为：卫星为完成定点拍照任务，需要进行25s/60°姿态机动，故边值约束表示为：

(8)

式中：ωi0,ωif分别为角速度状态的初值及终值，qj0,qjf分别为四元数状态初值及终值。

路径约束为卫星姿态机动过程中需满足的约束条件，以保证姿态机动过程能够满足任务要求，且减小柔性振动，具体包括卫星角速度、输出力矩和柔性振动三个约束条件，具体表示为：

1)角速度约束：卫星姿态机动过程中，若卫星角速度过大，会导致姿态传感器失效，无法准确获取卫星实时姿态，因此需要对角速度进行一定限制(rad/s)：

-0.07≤ωi≤0.07(i=1,2,3)

(9)

2)输出力矩约束：考虑到在轨运行的航天器自身执行机构物理条件上的限制，在姿态大角度机动过程中可能会出现超出执行能力上限的现象，因此需要建立执行机构控制输入约束(Nm)：

-10≤ui≤10(i=1,2,3)

(10)

3)柔性振动约束：为避免姿态大角度机动过程中引起剧烈柔性附件振动，考虑机动稳定性目标，确定振动约束，保证航天器不会因为过大的振动而发生失稳现象：

(11)

性能指标：包括机动时间及振动强度在内的多优化目标。其中，由于本文设定的任务为完成25 s/60°的姿态机动，故机动时间指标固定为25 s；在保证机动快速25 s基础上，最大限度减小柔性振动，保证系统稳定性，故另一个性能指标设定为：

(12)

2.2 姿态机动轨迹求解

基于式(8)～(12)建立的多目标多约束条件，需要进行姿态机动轨迹的优化求解。与其他数值优化方法相比，高斯伪谱法求解速度更快、精度更高。因此，本文将利用高斯伪谱法结合序列二次规划方法进行轨迹优化，得到兼顾快速性及稳定性的姿态机动轨迹。

Step1：利用高斯伪谱法完成对航天器姿态机动优化模型、性能指标和约束条件的离散化过程，从而将优化问题的求解转化为非线性规划问题的求解。

Step2：通过成熟的序列二次规划算法进行求解，得到期望的姿态机动轨迹，如图2所示，由图中可以看出，航天器可以完成25 s/60°的姿态机动。

注1. 高斯伪谱法求解速度快，精度高。近几年来，高斯伪谱法已在实际工程中进行多次应用[20-21]，用于完成如国际空间站大角度姿态调整等多次航天任务，具有十分重要的工程应用价值。

图2 姿态角速度机动优化轨迹Fig.2 Optimal maneuver trajectory of attitudeangular velocity

3 输入成形器

本节设计新型输入成形器FRIS，相比传统输入成形器，FRIS具有更短的作用时间，且对处理柔性实际频率变化的鲁棒性更强。

ZV输入成形器为最基本的输入成形器形式，当外界干扰等作用导致系统实际振动频率与固有频率不一致时，会影响ZV的作用效果，因此在ZV基础上，提出一系列具有鲁棒性的输入成形器形式，如：ZVD,EI等，其中，最常用的ZVD输入成形器由两个ZV输入成形器卷积得到，其数学表示形式为:

(13)

为缩短ZVD的作用时间，提出一种新型的输入成形器形式—FRIS如下：

(14)

(15)

考虑到

(16)

类似可得

(17)

将式(16)～(17)代入式(15)可得

(18)

(19)

由文献[23]可知，φ通常取为0.05。综合考虑振动抑制及作用时间的矛盾，选择ε=0.1，同时保证两者相对较优，从而得到FRIS与ZVD的振动抑制效果对比图，如图3所示，由此可知FRIS具有更强的鲁棒性。此外，由式(13)和式(14)可知，FRIS比ZVD作用时间更短。

图3 FRIS及ZVD的抑制效果对比图Fig.3 Comparison of suppression effects of FRIS and ZVD

考虑柔性动力学模型式(6)，基于获得的FRIS式(14)，设计压电致动器电压输入：

(20)

通过加入输入成形器作用，保证姿态机动过程中产生的柔性振动响应能够互相抵消，从而达到振动抑制的目的。

4 自适应连续终端滑模控制器设计

基于优化获得的姿态机动轨迹，考虑输入成形器对柔性振动抑制后的残余振动影响，本部分将设计一种自适应连续终端滑模控制器，有效处理外界干扰及残余振动对系统的影响，实现对姿态机动轨迹的高精度快速跟踪。

设计如下非奇异终端滑模面：

s=ωe+k1·β(qev)

(21)

(22)

基于式(5)及(21)，得到滑模动态表达式为：

(23)

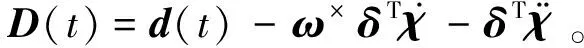
设计自适应连续终端滑模控制器：

(24)

式中：k(t)通过如下双层自适应律获得：

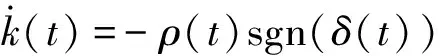
(25)

ρ(t)=r0+r(t)

(26)

(27)

(28)

e(t)=qa1/α-r(t)

(29)

定理1. 针对柔性航天器系统式(4)～(5)，若设计连续终端滑模控制器式(24)，采用如式(25)～(27)所示的自适应律，则可保证航天器姿态四元数跟踪误差qev及角速度跟踪误差ωe在有限时间内收敛至0。

证. 将式(24)代入式(23)可得：

(30)

令ν=z(t)+D(t)，则式(30)转化为：

(31)

Step1: 选取Lyapunov函数为

(32)

(33)

(34)

因此，基于式(34)，根据文献[24]中有限时间收敛定义，可得有限时间内δ=0，即

(35)

故系统状态将在有限时间收敛到滑模面s。

ωe=-k1·β(qev)

(36)

选取Lyapunov函数为：

(37)

对上式求导可得：

(38)

因此，系统姿态角跟踪误差qev及角速度跟踪误差ωe会在有限时间收敛到0。定理1得证。

5 仿真校验

为校验轨迹优化设计-输入成形器-有限时间控制器综合方法的有效性，进行有无IS情形下的对比仿真校验与分析，仿真过程中各参数选取如下：

所受到的干扰设置为：

d=

航天器姿态及角速度初值为：

考虑前两阶柔性振动模态，则耦合矩阵δ为：

柔性模态参数为：Λ1=0.7681 rad/s,Λ2=1.1038 rad/s,ξ1=0.0056，ξ2=0.0086。

FRIS设计为：

控制器参数选取如下：λ=10,r0=1,γ=0.2,q=1.5,α=0.5。

为校验本文所设计算法的有效性，对比了无输入成形器的ACTSMC及有输入成形器下的ACTSMC(ACTSCM-IS)的作用效果。仿真结果如图4～图7所示。图4及图5为姿态四元数与姿态角速度的跟踪曲线图，通过图4及图5可以看出不加IS时，所设计的ACTSMC可以实现对系统姿态的快速跟踪，但是由于柔性振动未主动抑制仍然存在，控制精度低，而加入IS后可以保证更高精度。

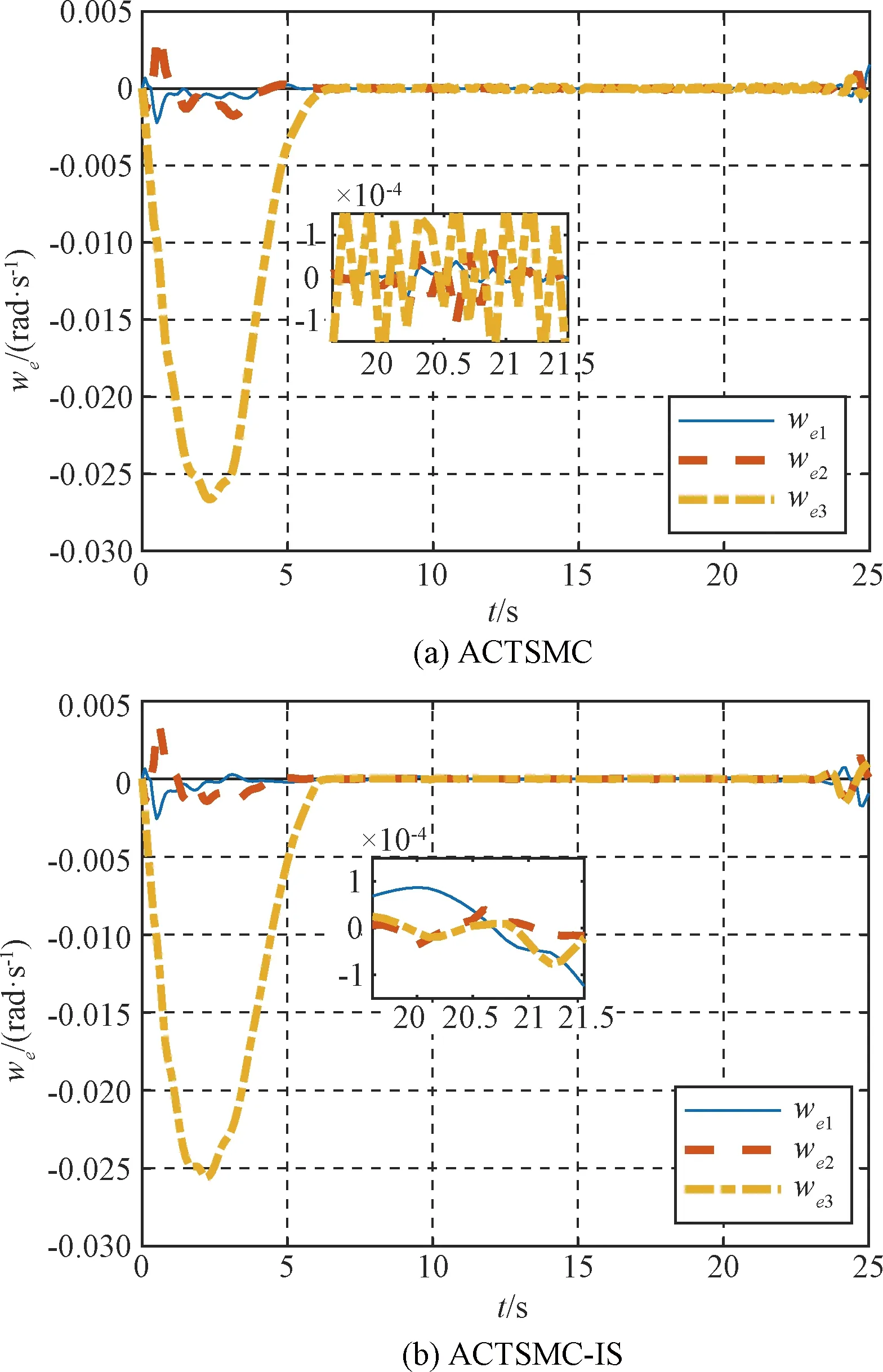
图5 姿态角速度跟踪曲线图Fig.5 Tracking of attitude angular velocity

图6为控制输入变化曲线图，从图中可以看出控制输入满足约束条件，未加输入成形器时，柔性振动会对刚体运动产生影响，从而导致控制输入出现大的波动；而在利用输入成形器对柔性振动进行有效抑制后，能够减小了柔性振动对刚体运动的耦合作用，且所设计的自适应算法避免了增益过估计问题，保证控制输入更光滑，更适合于工程实际。

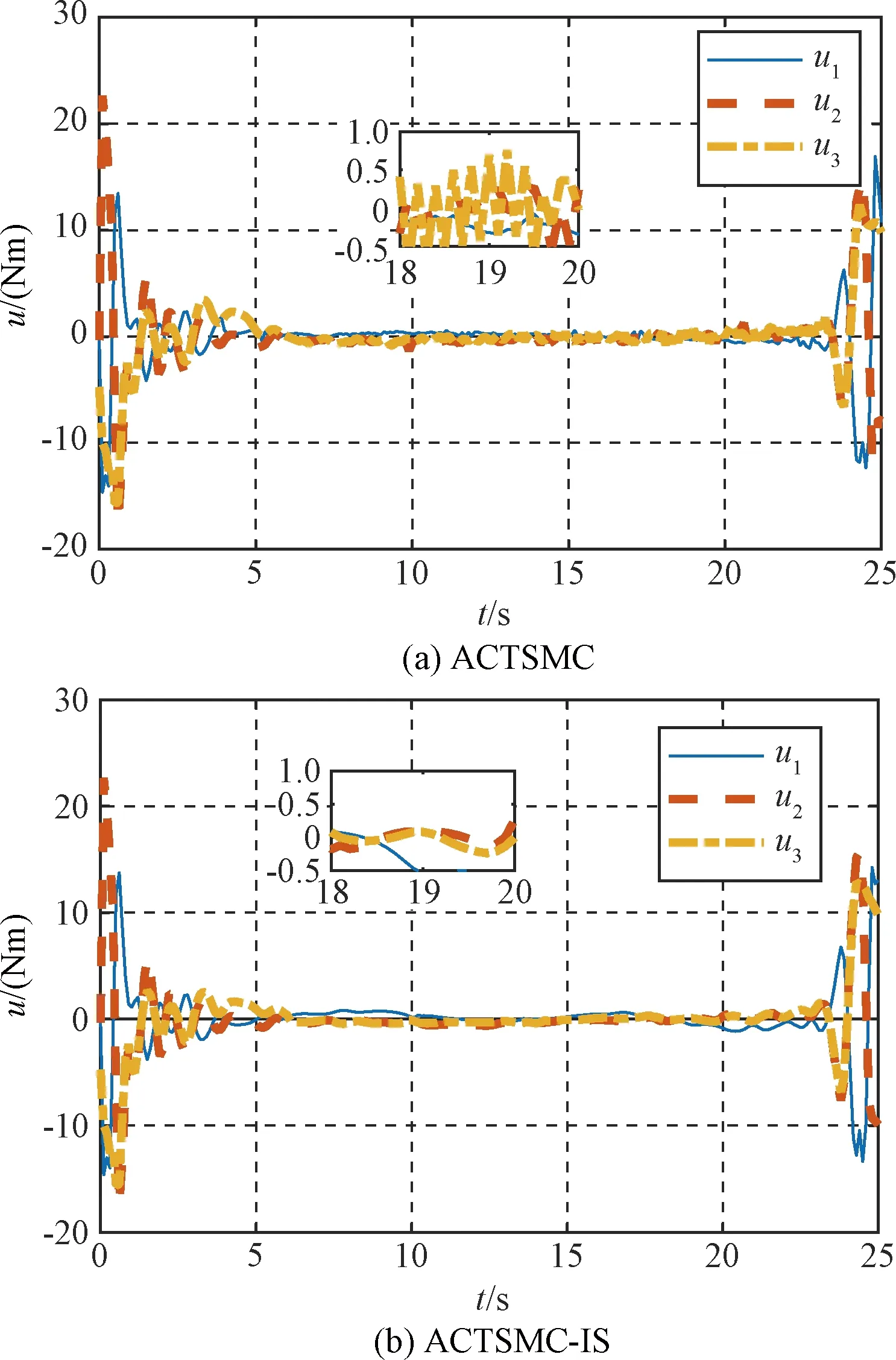
图6 航天器控制输入图Fig.6 Control inputs of spacecraft

考虑到第一阶柔性模态对航天器稳定的影响最大，故本文主要考虑利用IS对一阶柔性模态进行抑制，传统ZVD与FRIS对柔性振动抑制的对比曲线如图7所示，可以看出FRIS作用时间短，且具有更好的振动抑制效果。因此，通过仿真可以校验，本文所设计优化控制综合方法能够实现航天器姿态高精度、快速机动控制，且有效抑制柔性附件振动。

6 结 论

对于带有大型柔性附件的航天器系统，考虑到其大角度机动过程中“快速性”及“稳定性”矛盾，本文利用优化与控制综合方法，设计出兼顾快速性及稳定性的姿态机动轨迹，并提出一种既能减小作用时间、又能提高鲁棒性的新型输入成形器，结合双层自适应连续终端滑模控制器，可以保证柔性振动的主动抑制，实现对姿态优化轨迹的快速高精度跟踪。文中给出的仿真实例说明了该方法的有效性。