PCE方法在空间实验室轨道预报误差分析中的应用

欧阳琦，陈 明，李翠兰，李 勰

(北京航天飞行控制中心，北京 100094)

0 引 言

随着人类航天活动的日益频繁，在轨空间目标数量不断增加，对航天器的在轨管理以及后续的航天任务带来了新的挑战。航天器在轨运行管理期间，一方面需要协调测控资源对其进行跟踪，另一方面还需要计算与其他空间目标的相对位置关系以进行有效地碰撞预警，因此，对航天器轨道预报的误差进行分析至关重要。

航天器轨道预报是根据航天器初始时刻状态进行动力学积分的过程。在这个过程中，由于知识缺乏、航天器所处的环境客观可变，航天器初始时刻的状态、动力学模型等都存在不确定性。对这些不确定性的度量以及其在轨道预报中传播规律的研究是轨道预报误差分析的关键。传统的轨道预报误差分析方法大都基于线性模型或蒙特卡洛仿真方法(Monte Carlo simulation, MCS)[1-2]。基于线性模型的方法也称为线性传播方法，这种方法计算效率高，然而对于非线性程度较强的系统以及中长期预报来说，精度较差；MCS方法精度较高，然而需要大量的样本点才能计算得到高精度的计算结果，计算效率低。为克服上述方法的不足，近年来许多学者对轨道动力学中非线性不确定性传播方法进行了研究[3-4]。多项式混沌展开法(Polynomial chaos expansion，PCE)起源于Wiener和Ito对于无序运动的数学描述，属于随机展开法中的一种，实质上是对随机变量构建一个具有随机性的近似模型[5]。该方法在结构设计[6-7]、流体力学[8-9]等领域得到了广泛的应用。近年来，Jones等[10]将PCE方法应用于轨道预报误差分析之中，并对太阳同步轨道和闪电轨道的轨道误差传播进行了测试，验证了该方法的有效性。

2016年9月15日，天宫二号空间实验室及其搭载的空间应用系统发射升空，对我国未来空间站建设的关键技术进行了验证[11-12]。空间站质量体积大、空间构型复杂、组合体运行模式多变，对其在轨管理技术难度较大。本文将PCE方法应用于空间实验室轨道预报的误差分析，为我国未来空间站的建设和在轨管理提供有益参考。

1 PCE方法简介

本节对PCE方法进行简要介绍，包括PCE模型、PCE方法的应用形式、PCE系数的求解以及随机变量统计信息的求解几个部分[13]。

1.1 PCE模型

采用PCE，任意分布的随机变量u可以展开为：

(1)

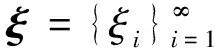
(2)

PCE方法均方收敛。当p≠q时，Γp与Γq正交，极大简化了均值及方差等信息的计算过程。为了实际应用的需要，通常截取到一定阶数。将ξ的个数定义为PCE的维数，Γ的个数即PCE的阶数，则d维p阶PCE模型涉及的系数个数P为：

(3)

在实际运用中，通常采用更加简洁的形式：

(4)

式中：bi与系数ai1,…,aip以及Ψi(ξ)与函数Γp(ξi1,…,ξip)之间是一一对应关系。

1.2 PCE方法的应用形式

PCE方法一般有侵入式与非侵入式两种应用形式。侵入式方法将系统模型中的不确定性变量进行随机展开，并将其代入系统分析模型中；非侵入式方法将系统模型作为黑箱处理，直接对系统的输出进行随机展开，建立系统输出对不确定性输入变量的显式表达式。对于轨道预报来说，若航天器初始位置速度存在不确定性，侵入式方法将位置速度近似成一系列随机变量的展开形式，轨道动力学方程也需要修改成一系列随机变量的方程；非侵入式方法则将轨道预报过程看作一个黑箱，不对轨道动力学方程进行修改，通过生成一系列样本点来构建预报时刻的航天器位置速度与初始时刻航天器位置速度的不确定性传播关系。由于非侵入式方法无需对轨道动力学方程进行修改，一方面在工程应用中不需要修改现有代码，另一方面也避免了方法研究与实际对象的耦合关联，与侵入式方式相比应用范围更广，因此本文采用非侵入式PCE方法。

1.3 PCE系数的求解

对于非侵入式PCE方法，其系数求解时需要生成一系列样本点，计算每个样本点处的输出变量值，从而构建待定系数的求解方程。常用的样本点生成方法有蒙特卡洛仿真法、正交试验设计法(Orthogonal array sampling, OAS)和拉丁超立方法(Latin hypercube design, LHD)等[13]。其中，拉丁超立方法是一种分层抽样法，可以生成分布较为均匀的样本点，通过较少的抽样次数就可以获得较好的精度。本文采用拉丁超立方法生成样本点。给定一组样本及其对应输出变量值，可以计算PCE模型中的待定系数。目前发展了多种求解待定系数的方法[14]，其中Galerkin投影法和回归法是两种主要求解方法。Galerkin投影法通过利用多项式的正交性，进行内积操作将函数分别投影到每个基函数项上，得到相应系数。回归法则是通过最小化某些样本点上PCE预测响应值和真实响应值间的误差平方和来求解PCE中的待定系数。本文采用回归法求解PCE中的待定系数。具体步骤如下：

(1)随机选取N个样本点{ξ1,ξ2，…,ξn};

(2)计算样本点对应的响应值{y1,y2…，yn}，其中，yi=u(ξi),i=1,…,n，从而构建如下方程:

Ab=Y

(5)

式中：

1.4 统计信息的求解

当PCE模型中的系数确定后，便可以方便快速地得到随机变量的均值、方差等统计信息，如下：

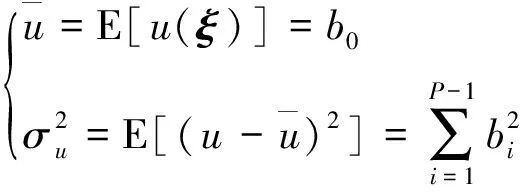
(6)

另外，若要计算随机变量的高阶矩或概率分布，可以通过蒙特卡洛仿真方法随机产生一系列样本点并计算PCE模型输出值，进而计算相应的统计信息。

2 基于二体模型的轨道预报误差传播

2.1 问题描述

本节将PCE方法应用于空间实验室轨道预报误差分析。PCE模型精度主要受PCE模型阶数、预报时长以及样本点的数目这几个因素的影响，因此本节针对以上因素展开讨论。考虑工程应用的需要，本节考察预报时长为1天和7天。表1给出了历元时刻2018- 03-17T08∶00∶00.000的初始位置和速度值。假设J2000坐标系下的初始位置和速度存在误差，标准差分别为10 m和1 m/s。为简化模型，本节的轨道预报模型基于二体假设。

表1 空间实验室初始位置速度Table 1 Initial state for the space laboratory

2.2 PCE模型阶数

为考察不同阶数PCE模型的精度，首先将样本点的数目设置为10000。各样本点对应的初始轨道根据其概率分布计算得到。由于仅位置和速度存在误差，因此PCE模型维数d=6。采用不同阶数的PCE模型进行预报，分别预报1天、7天，并统计均值和标准差。图1给出了不同阶数PCE模型计算结果的相对变化值。从图1可以看出，随着PCE阶数的增加，均值和标准差的计算结果相对变化逐渐减小。预报1天时7阶PCE模型相对于6阶PCE模型均值相对变化为10-14量级，标准差相对变化为10-11量级；预报7天时7阶PCE模型相对于6阶PCE模型均值相对变化为10-8量级，标准差相对变化为10-7量级。

图2给出了7阶PCE模型各项系数的归一化值|bi/b0|。若系数归一化值不收敛，说明需要更高阶的PCE模型才能够达到较好的近似效果。从图2可以看出，随着项数的增加PCE系数值逐渐减小，PCE方法趋于收敛。与预报7天相比，PCE系数收敛速度在预报1天时更快。在同样的精度指标要求下，预报时间越长，所需PCE模型阶数越高。实际工程应用中，越高阶的PCE模型项数越多，计算量越大，因此PCE阶数的选择需要综合考虑精度和计算效率的影响。

2.3 样本点数目

为考察样本点数目对PCE模型的精度影响，本节的样本点数目设置为可计算得到PCE模型系数的最少样本点数目。参照第2.1节，d维p阶PCE模型所需的最少样本点数目为(d+p)!/(d!p!)。与第2.2节中10000个样本点的结果进行比较，结果如图3所示。从图3可以看出，PCE模型阶数越低，采用最小样本点计算得到的相对误差越大。预报1天时4阶PCE模型的标准差相对误差达到10-5量级；预报7天时5阶PCE模型的标准差相对误差达到10-5量级。综合考虑精度和计算效率的影响，5阶PCE模型效果最佳。

图1 PCE模型计算结果相对变化值(基于二体模型)Fig.1 Relative difference in the PCE results (using the two-body model)

图2 7阶PCE模型各项系数归一化值(基于二体模型)Fig.2 Normalized coefficients for the seven order PCE model(using the two-body model)

2.4 与MCS方法的比较

工程应用中，MCS方法是轨道预报误差分析采用较为广泛的一种方法，该方法需要较多的样本点才能满足一定的精度要求，本节将最小样本点的5阶PCE方法与MCS方法进行比较，验证PCE方法的计算效率和精度。

图4给出了MCS方法计算结果相对于样本点数目的变化值。图5给出了PCE方法与MCS方法的比较结果(仅给出了标准差，均值结果类似)。可以看出，随着样本点数目的增加，MCS方法的计算结果趋于收敛至PCE方法的计算结果。MCS方法使用10000个样本点才能达到10-4量级的收敛精度，其收敛速度较慢。5阶PCE方法只需要462个样本点便可以达到10-5量级的收敛精度，PCE方法收敛所需的样本点明显少于MCS方法，PCE方法计算效率更高。

图3 PCE模型结果比较(基于二体模型)Fig.3 Comparison of the PCE results (using the two-body model)

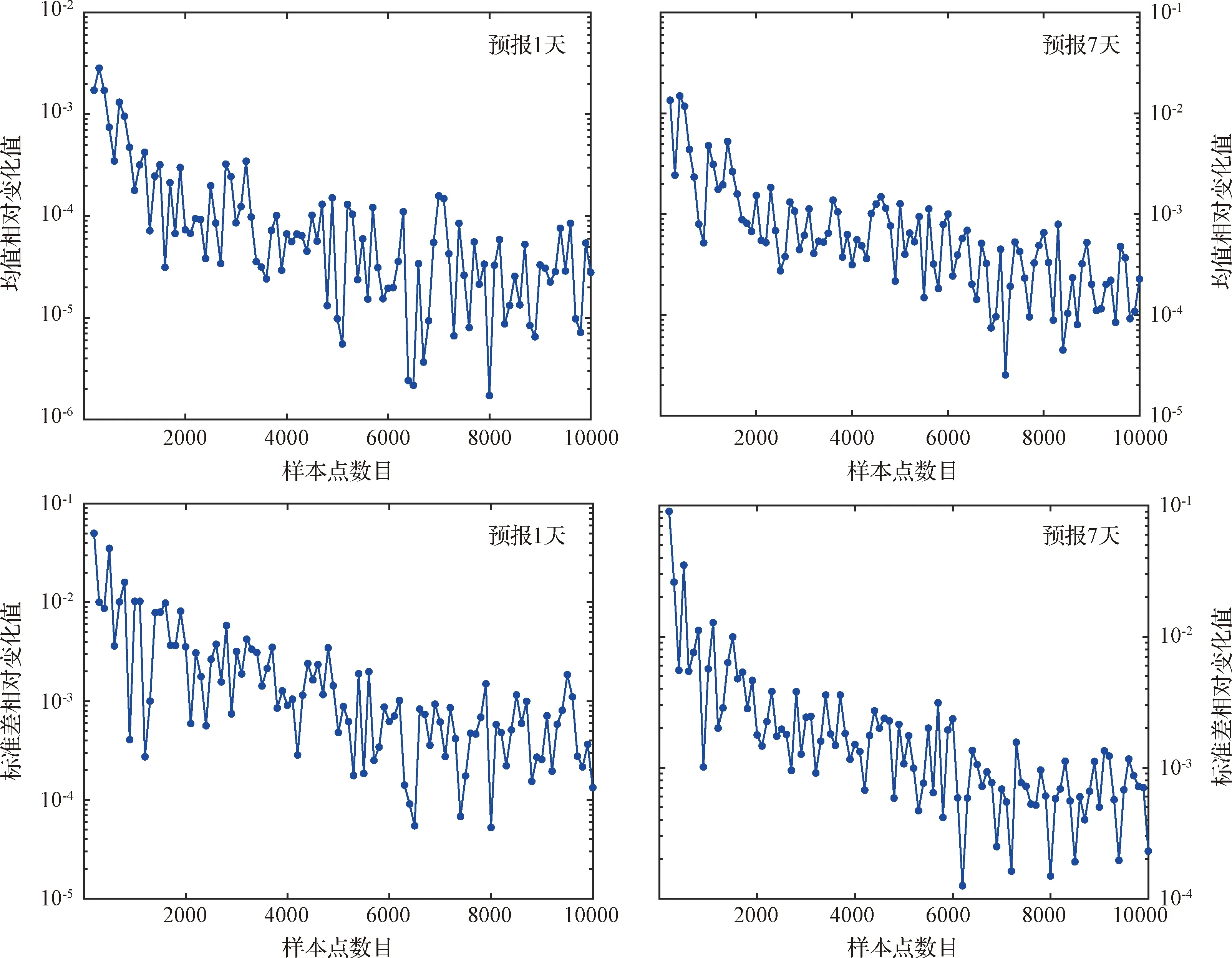
图4 MCS结果相对变化值(基于二体模型)Fig.4 Relative difference in the MCS results (using the two-body model)

2.5 与线性传播方法的比较

线性传播方法把不确定性传播模型近似为线性，因此当初始位置和速度服从正态分布时，通过轨道预报后的位置速度仍然服从正态分布。表2中比较了最小样本点的5阶PCE方法与线性传播方法的计算结果。预报1天时均值偏差较小，Y，Z和Vx的标准差偏差较大，Z的标准差尤为明显；预报7天时均值和标准差的偏差都较大。

第2.4节中采用MCS方法计算了10000个样本点预报1天和预报7天后的位置速度，其分布如图6所示。预报1天和7天后位置速度的分布都有一定程度的倾斜，预报1天后Z方向位置的分布较为明显。初始位置和速度误差在经过一段时间的传播之后，不再服从正态分布，因此，采用线性传播方法计算前两阶矩将会带来较大的误差。

图5 PCE与MCS的结果比较(基于二体模型)Fig.5 Comparison of the PCE and MCS results(using the two-body model)

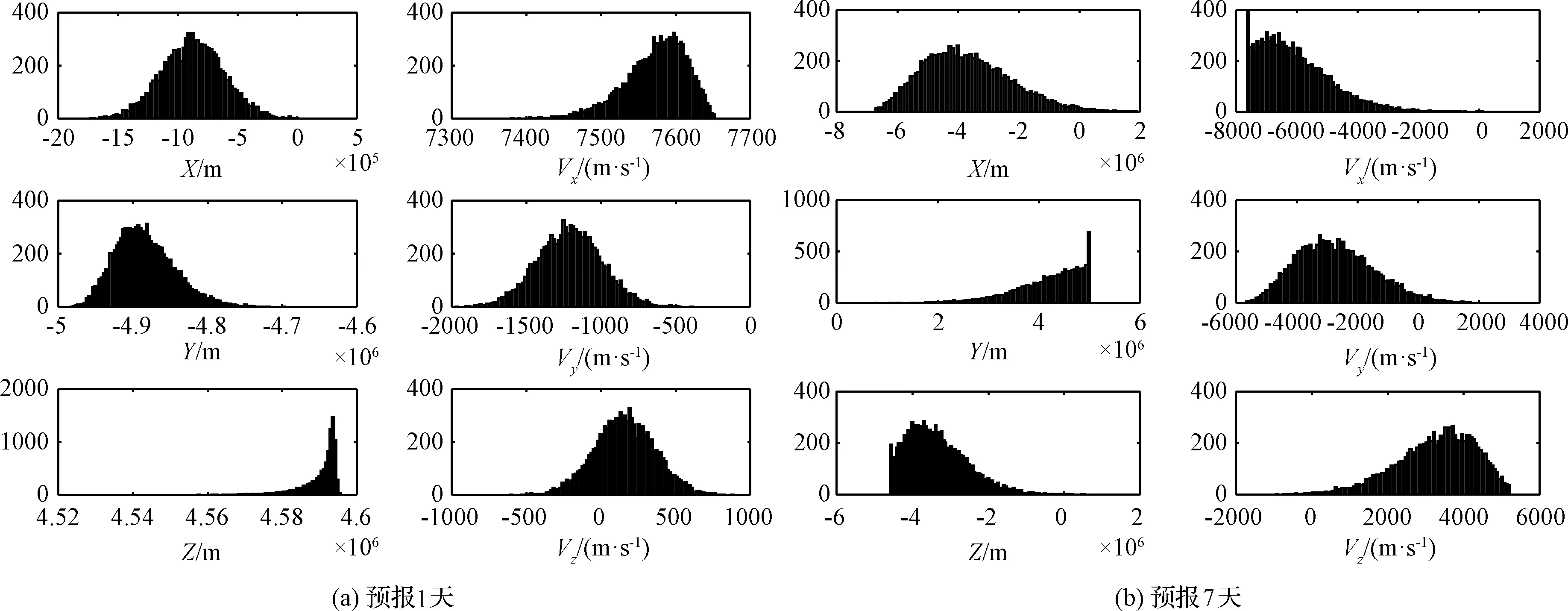
图6 位置速度分布Fig.6 Distribution of positions and velocities

表2 PCE方法与线性传播方法的比较(基于二体模型)Table 2 Comparison of PCE and linear propagation method(using the two-body model)

通过PCE方法构建了轨道预报不确定性传播的近似模型。该模型只是简单的多项式计算，相比于原本的轨道预报模型计算效率显著提高。通过构建好的PCE模型，不仅能够计算得到位置速度的前两阶矩，还能够快速给出位置速度的分布。采用PCE模型计算第2.4节中10000个样本点预报1天和预报7天后的位置速度，并与MCS的计算结果进行对比。图7为轨道坐标系(RTN坐标系)下的散点密度图。采用PCE模型计算得到的概率分布几乎和MCS方法得到的概率分布一致，PCE方法构建的不确定性传播模型能够很好地近似轨道预报中的不确定性传播，验证了PCE方法的有效性。工程中通常用线性传播方法计算得到的标准差构建3σ概率椭圆来描述轨道位置的不确定性[15]，因此图7也给出了3σ概率椭圆的结果。从图7可以看出，采用3σ概率椭圆来描述轨道预报后的位置分布并不精确，径向(R方向)误差相对较大。

图7 PCE和MCS结果分布图，以及3σ概率椭圆(基于二体模型)Fig.7 Distribution of PCE and MCS solutions, along with 3σ probability ellipsoids (using the two-body model)

3 基于高精度模型的轨道预报误差传播

本节进一步采用高精度轨道预报模型对PCE方法的近似效果进行考察。初始位置和速度与第2节相同，见表1。考虑初始位置、速度以及大气阻力系数CD存在误差，标准差分别为10 m、0.01 m/s和0.1，CD均值设为2.0。考察预报1天和7天。PCE模型维数d=7。

与第2节类似，本节使用10000个样本点和最小样本点构建了不同阶数的PCE模型，并进行了比较。图8给出了10000个样本点下5阶PCE模型系数各项系数归一化值，可以看出，在100项之后，系数值的量级都在10-10左右波动，增加PCE模型的阶数并不能显著提高近似效果。3阶PCE模型总项数为120项，综合考虑精度和计算效率的影响，选取3阶PCE模型。通过对比最小样本点下不同阶数PCE模型的计算结果得到，预报1天时3阶PCE模型相对于2阶PCE模型均值相对变化为10-11量级，标准差相对变化为10-8量级；预报7天时3阶PCE模型相对于2阶PCE模型均值相对变化为10-10量级，标准差相对变化为10-7量级。

图9给出了PCE方法与MCS方法的比较结果(仅给出了标准差，均值结果类似)，随着样本点的增加，MCS方法计算结果逐渐趋于PCE方法的计算结果，且MCS方法的收敛速度较慢，所需样本点数目较多。

图9 PCE与MCS的比较(基于高精度模型)Fig.9 Comparison of the PCE and MCS (using the higher fidelity model)

图10对比了轨道坐标系(RTN坐标系)下PCE、MCS以及线性传播方法得到的结果。PCE模型计算得到的概率分布几乎和MCS方法得到的结果一致。本节中初始速度误差比第二节中小两个量级，预报1天时采用线性传播方法得到的3σ概率椭圆也能够较好地描述位置速度的概率分布，但在预报7天时误差相对较大。通过与MCS方法及线性传播方法的对比可知，PCE方法能够很好地解决基于高精度模型轨道预报误差传播的问题，验证了PCE方法的有效性。

4 结 论

本文以空间实验室为研究背景，将PCE方法应用于轨道预报误差分析。通过构建PCE模型对轨道预报的不确定性传播过程进行近似，进而对轨道预报后航天器位置和速度的误差进行分析。针对二体模型和高精度模型，分析了不同PCE模型阶数、预报时长以及样本点的数目对构建PCE模型的影响。将PCE方法与MCS方法和线性传播方法进行了对比，结果表明PCE方法有较好的非线性近似能力，且计算效率要明显高于MCS方法，验证了PCE方法应用于空间实验室轨道预报的有效性。

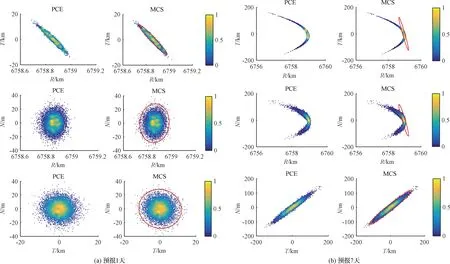
图10 PCE和MCS结果分布图，以及3σ概率椭圆(基于高精度模型)Fig.10 Distribution of PCE and MCS solutions, along with 3σ probability ellipsoids (using the higher fidelity model)

本文的轨道预报只考虑了初始时刻位置速度、以及大气阻力系数的不确定性。在本文的研究基础上可以进一步细化不确定性模型，考虑例如重力场、光压、空间环境等模型参数存在不确定性时对构建PCE模型所带来的影响。另外，本文在样本点的选取上使用了最小样本数目的方式，还可以进一步研究根据轨道动力学中不确定性的传播规律序贯添加样本点以达到更好的近似效果和计算效率。本文的研究工作为这些问题的研究提供了较好的基础。