低轨Walker星座构型演化及维持策略分析
2019-12-03赵灵峰刘会杰
陈 雨,赵灵峰,刘会杰,李 立,刘 洁
(上海微小卫星工程中心,上海 201210)
0 引 言
高覆盖率、超短重访间隔等使用需求使新的卫星项目中从数十颗到数百颗的卫星星座被提出,得到了学者们的广泛研究[1-3]。其中,Walker星座以其在全球范围内纬度带覆盖、均匀的重访特性而被广泛应用,例如美国的GPS全球导航定位系统、俄罗斯的Glonass导航系统以及北斗导航定位系统等[4]。理论上Walker星座中卫星之间的相对位置关系保持不变,但是由于卫星的入轨偏差及摄动力的不同,导致星座构型发散,从而影响星座的覆盖特性及任务实现,针对这种大型卫星星座的构型演化规律分析及维持策略成了制约卫星星座发展的关键技术[5-7]。目前国内对卫星星座构型的研究主要针对中高轨星座的理论分析,文献[8]分析了中高轨卫星由地球扁率和入轨偏差引起的星座几何构型演化过程,文献[9]建立了中高轨卫星星座轨道摄动补偿控制的绝对和相对控制方程,对中高轨卫星星座的构型维持具有良好效果,但对卫星入轨精度有较高要求,在低轨卫星中难以实现;文献[10]针对主从式卫星集群系统的空间构型长期保持问题设计了具有较强适应性的控制逻辑与基于李雅普诺夫稳定性理论的控制器;文献[11]考虑J2项摄动的影响,设计了具有鲁棒性的环绕星相对轨道及相对轨道控制方法。国外文献中,文献[12]提出了选取卫星相对以“平均星座”作为标称相位的圆轨道星座维持方法;文献[13]利用线性二次控制器来实现星座的位置保持;文献[14]研究了星座控制的结构和算法,将燃料和时间均衡作为目标来进行优化设计,研究都尚处于理论阶段,且计算复杂,不利于工程应用实现。
本文结合国内某首例低轨Walker卫星星座在轨轨道实测数据,对低轨Walker星座的构型演化规律进行理论分析及仿真,并采取一种基于基准卫星的相对相位维持策略对星座构型进行维持。经过工程应用验证,相比于星座绝对构型维持,基于基准星的相对相位维持策略降低星座构型维持的复杂度,大大减少需要维持的卫星的数量及维持频次,对目标卫星仅实施一次轨道高度控制,实现卫星间相对相位的调整,不仅节约燃料,且缩短轨控时间。
1 轨道摄动及星座构型演化分析
Walker-δ星座的概念最早由英国皇家飞行研究中心的沃克提出[15]。Walker-δ星座构型用参考码T/P/F表示,其中,T表示星座中卫星的总数目,P表示卫星分布的轨道面数,F是用来确定相邻轨道面卫星相对相位的因子。Walker-δ星座中所有卫星呈均匀对称分布,同一个轨道面内卫星分布均匀,不同轨道面间卫星的相位(即纬度幅角)保持一定的相对关系,相邻轨道面对应序号卫星的相位差为Δu=360°·F/T,其中F=0,1,…P-1。
1.1 卫星轨道摄动分析
卫星在空间除了受到地球引力外,还受到各种摄动力的作用,其在空间的运动可以用式(1)常微分方程表达[16]。
(1)
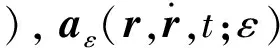
针对低轨卫星,受到的摄动力影响较大的主要是地球扁率摄动和大气阻力摄动,其它摄动为小量,可以忽略。仅考虑地球中心引力和扁率项摄动时,卫星轨道平均根数长期变化率如式(2)所示。
(2)
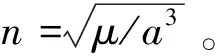
面质比为S/m的航天器受到大气阻力的阻尼加速度为[17]:
(3)
其中,CD为阻尼系数,ρ为航天器所在位置处的大气密度,V为航天器相对大气的速度,V为其大小。大气阻力主要引起卫星半长轴和偏心率摄动,其长期变化率如式(4)所示。

(4)
式中:Fρ=CD(S/m)ρ,f为卫星真近点角。
大气阻力摄动引起的半长轴和偏心率变化取决于大气密度和卫星面质比,高层大气密度一般随卫星轨道高度的升高而减低,同时也受季节、太阳活动、时间以及地磁活动的影响。
1.2 LEO卫星星座构型演化
由式(2)可知,低轨卫星在只考虑地球扁率J2项摄动时,对于轨道高度、倾角以及偏心率三个参数完全一致的Walker星座的一组卫星,升交点赤经和相位的长期变化率相同,此时Walker星座中的卫星在空间内的相对位置关系即星座空间构型维持不变。但由于发射时入轨偏差及星座组网相位捕获误差的影响,卫星之间的轨道参数存在初始误差,且轨道高度偏差将导致卫星所受大气阻力摄动的差异,引起卫星间相对升交点赤经和相位的变化。
设两颗卫星的入轨轨道参数偏差为(Δa1,Δe1,Δi1,ΔΩ1,Δλ1),由于卫星入轨轨道高度不同引起卫星所受大气阻力摄动的差异使得卫星间轨道衰减偏差为Δa2,对于小偏心率的圆轨道卫星,忽略偏心率的影响,由入轨偏差和衰减偏差引起的卫星间升交点赤经和相位相对变化率如下所示:
(5)

(6)
式(5)~(6)中,升交点赤经和相对相位变化率的大小除了受初始轨道参数偏差影响外,还与卫星标称半长轴ai相关。设定轨道倾角偏差为0,仿真不同轨道高度卫星在不同半长轴偏差下的升交点赤经和相位角一年时间的漂移量如图1、图2所示。通过仿真可知,随着卫星轨道高度的增高,半长轴偏差对升交点赤经和相位漂移量的影响逐渐降低,对于低轨卫星,十米量级的半长轴偏差在一年时间会引起4°的相位漂移。
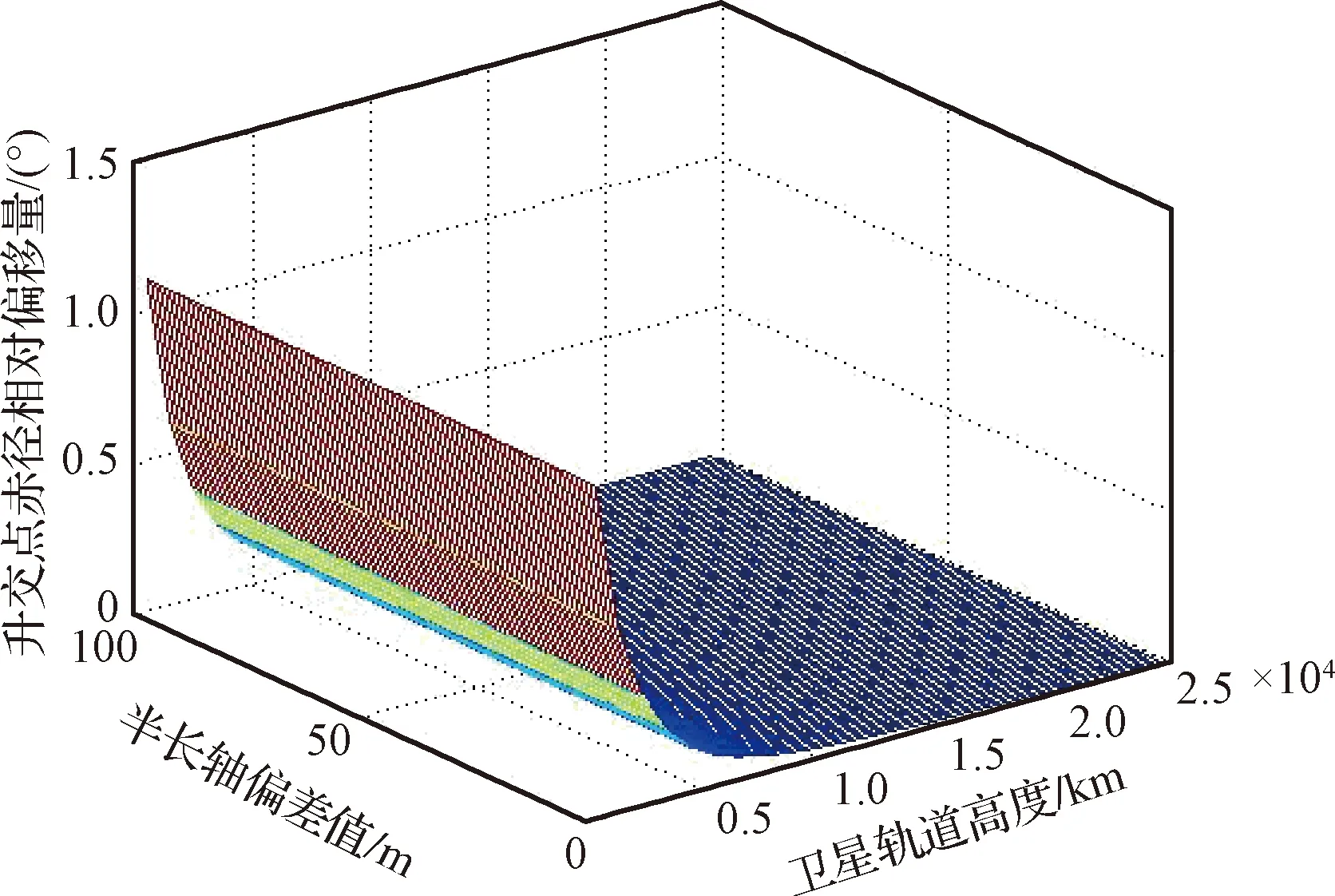
图1 升交点赤经漂移情况Fig.1 Drift value of RAAN
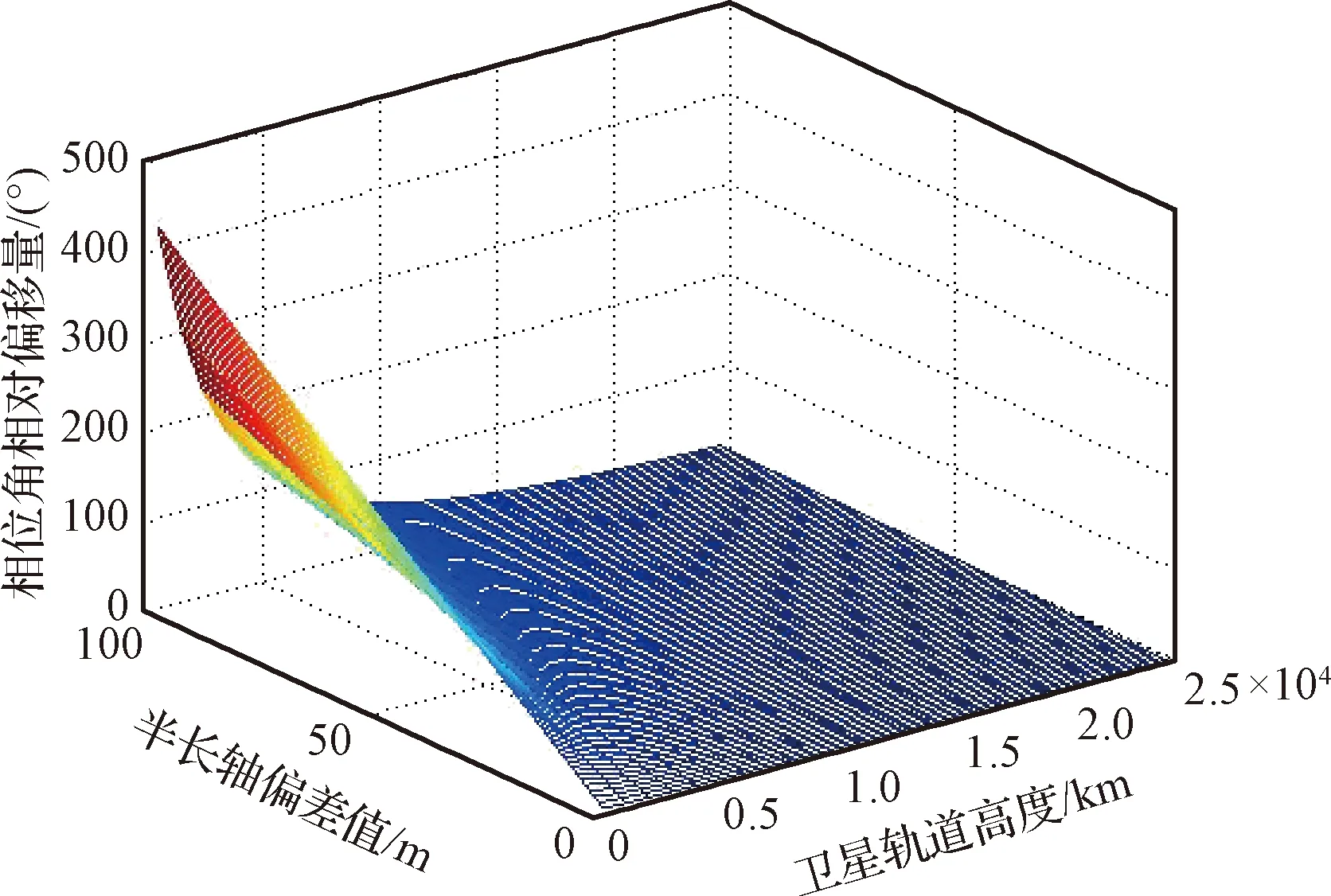
图2 卫星相位角漂移情况Fig.2 Drift value of relative phase
Δt时间后,卫星之间的相对升交点赤经和相位的变化量为:

(7)
式(7)表征了在地球扁率和大气摄动下由入轨偏差引起的卫星间相对相位漂移累积情况,卫星间相对位置发生变化,星座构型发散,整体服务性能恶化。
2 在轨实测数据分析
国内某低轨Walker星座于2018年初完成三批次9颗卫星发射入轨,实现星座组网。9颗卫星状态完全一致,在三个轨道面上均匀分布,形成标准Walker星座,实现对全球的均匀覆盖。本节整理了星座组网至今的实测定轨数据,分析低轨卫星轨道参数变化趋势及星座构型的演化情况。星座中卫星在八个月时间的轨道参数(平根数)累积漂移量如表1所示。表中卫星编号中“-”前的序号表示轨道面号,“-”后的序号表示此轨道面内的卫星序号。此星座卫星为圆轨道,表1中偏心率长期漂移量在10-5量级,近似于0,其影响可以忽略。
由于大气阻力摄动,卫星平半长轴随时间逐渐减小,以1-1卫星为例,轨道平半长轴在轨期间实际演化过程以及利用STK软件高精度轨道预报(High-precision orbit propagator,HPOP)模型仿真情况如图3所示,卫星半长轴衰减情况近似为线性,STK仿真中考虑了地球扁率与大气阻力,结果与实测数据吻合。卫星入轨后通过相位调整完成星座组网,相位捕获误差导致各卫星初始轨道半长轴存在差异,其中2-2卫星与3-3卫星半长轴相差最大,达到33 m。由表1可知,9颗卫星在轨期间半长轴衰减程度有所不同,其中3-3卫星初始半长轴最小,受到大气阻力摄动较高,其半长轴衰减量也略高于其它卫星,说明在同一时间段内星座中卫星所受大气阻力的大小主要受轨道高度影响。根据仿真外推结果,所有卫星在一年半的寿命期内半长轴衰减量预计不超过1 km。

图3 1-1卫星平半长轴变化与仿真情况Fig.3 Variation and simulation of 1-1 satellite semi-axes

表1 卫星轨道参数累积漂移量Table 1 Cumulative drift of satellites orbit parameters
卫星轨道倾角与升交点赤经在轨期间累计漂移量都较小,对星座构型的影响基本可以忽略。地球扁率摄动引起倾角的短周期变化,振幅0.1°,周期为60 d,当升交点赤经介于60°~240°之间时,倾角增大,当升交点赤经介于-120°~60°之间时,倾角减小。由于同一轨道面(即同一批次发射)卫星初始轨道倾角相同,不同轨道面初始倾角相差最大为0.08°,且相邻轨道面之间升交点赤经相差120°,导致相邻轨道面卫星的轨道倾角之差也随时间周期性变化,最大差值达到0.176°,如图4所示。
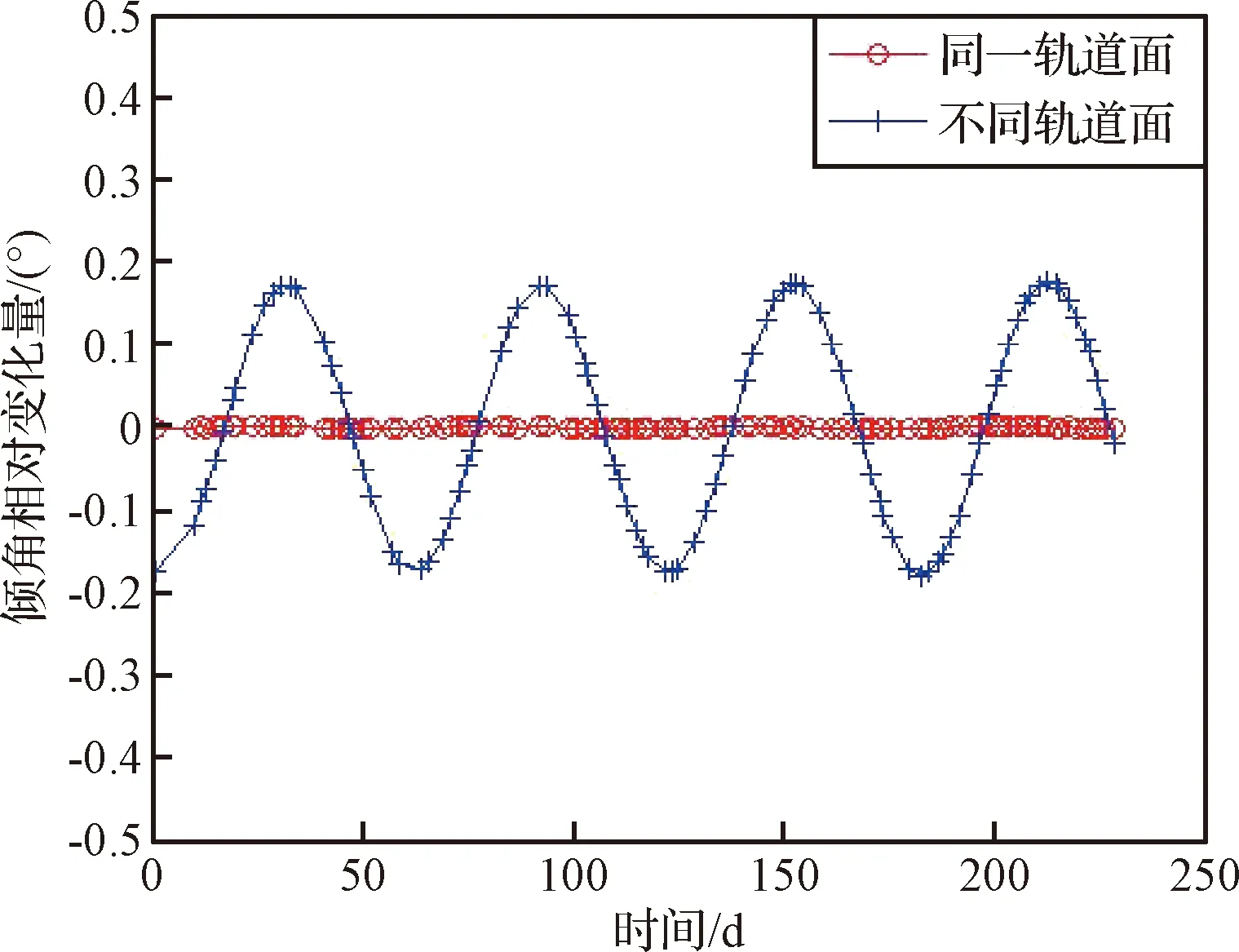
图4 卫星倾角差变化情况Fig.4 Variation of satellite inclination difference
卫星升交点赤经平均每天西退量较大,如表2所示,与地球扁率J2项摄动引起的升交点赤经西退理论计算值5.9621((°)/d)基本一致,不同轨道面的微小差异由三体引力和太阳光压引起。
卫星轨道参数中,相位角偏差不断累加,绝对漂移量接近40°,卫星位置远远偏离标称值。根据第1.2节星座构型演化规律分析,考虑卫星空间相对位置关系,取9颗卫星的平均轨道为参考轨道。得到各卫星相对相位角漂移量如图5所示。

表2 卫星升交点赤经西退情况Table 2 Variation of satellite RAAN
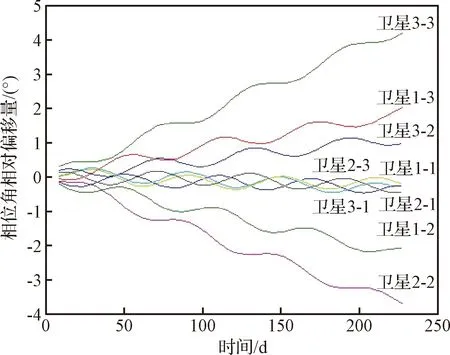
图5 相位角相对漂移量Fig.5 Drift value of relative phase
图5中相位角漂移同时受到轨道倾角和半长轴两个因素的影响:初始轨道半长轴与9颗卫星平均半长轴相近时,相位角相对变化主要体现为由倾角变化引起的周期项,周期为60 d,长期漂移量较小,如卫星1-1、卫星2-1和卫星3-1;初始半长轴与平均半长轴偏差较大时,相位角相对变化最终体现为长期漂移项,同时由于轨道倾角周期性变化的作用,相位角相对漂移量并非随时间线性增长,如卫星2-2与卫星3-3。由于初始轨道半长轴相对平均半长轴偏差的高度方向相反,卫星2-2与3-3相位角相对漂移方向也相反,累积漂移量分别为-3.8°和4.2°,平均相位角漂移率0.0165(°)/d、0.0183(°)/d,与理论计算结果基本一致。根据上文分析的轨道倾角变化规律,同一轨道面内卫星之间的倾角变化相同,相对相位角变化只由半长轴偏差引起,表现为线性的长期变化,而相邻的轨道面卫星间的相对相位角变化由半长轴差和周期变化的倾角差共同作用,长期演化过程为非线性,如图6所示。

图6 卫星间相对相位差漂移情况Fig.6 Drift value of relative phase difference
3 构型维持策略
通过对Walker星座构型的理论和在轨实测数据分析,卫星间初始轨道参数的偏差导致星座构型发散,影响星座的服务性能,需对卫星进行控制以维持星座构型的稳定。星座构型保持可分为绝对构型维持和相对构型维持两种方法[18],绝对构型维持将卫星控制在某一确定坐标系下的标称位置,通常需要补偿轨道半长轴和相位漂移,相对构型维持只维持所有卫星之间的相对位置关系,控制星间相位差在最大容许偏差范围内。
根据第二章轨道实测数据分析,卫星星座组网后轨道倾角及升交点赤经漂移均为小量,大气耗散力导致的半长轴衰减在寿命期内的衰减对卫星的覆盖性能并无影响,卫星绝对相位漂移量远远大于相对相位漂移量,绝对构型维持将计算复杂、维持频次多且耗费燃料,因此,对该卫星星座考虑相对构型维持方法,且只需对卫星相位角进行调整。基于前文数据分析,采取一种基于基准卫星的相对相位维持策略:选取一颗卫星作为基准卫星,使星座中其它所有卫星相对于基准卫星的相位漂移量累加值最小,以达到最低轨控频次的目的,具体步骤如下:
1)分别以1~9号卫星作为基准卫星,计算其余8颗卫星相对基准星的相位角漂移量:
(8)

2)分别计算以i号卫星为基准卫星时其余卫星相位角漂移量的累加值:
(9)

4)在卫星i相对基准卫星k的相位差临近阈值时,根据相位角漂移方向,对卫星i实施轨控,以基准卫星为标准,抬升或降低轨道高度,通过改变轨道半长轴改变卫星间相位漂移方向,实现相对相位的调整。根据式(6),忽略星间倾角差,卫星的半长轴调整量如式(10)所示。
(10)
式中:ξλ为相位差最大容许漂移量,ΔT为预期的相位漂移时间。
根据上述相位维持策略步骤,分别以某星座中1~9号卫星作为基准卫星,计算其它卫星的相对相位漂移量,如表3所示。

表3 卫星相对基准星相位漂移情况Table 3 Drift value of relative phase difference
根据表3,分别以1-1卫星和2-3卫星为基准卫星时,累计相位差相对漂移量较小。但以2-3星为基准卫星时,有三颗卫星相位差临界阈值,因此选择以1-1卫星作为基准卫星,只需对2-2卫星和3-3卫星实施轨控,根据式(10),并考虑一定轨控余量,计算得到分别将2-2星降低轨道高度40 m、3-3星升高轨道高度38 m。由于此次轨控对卫星半长轴的改变在几十米,对轨道偏心率的改变非常小,可以忽略,因此可以采取单脉冲变轨(若轨控量很大或对偏心率要求比较高,则根据霍曼转移定理需要两个脉冲完成变轨),在轨道面内卫星飞行方向施加正向或负向速度增量,如式(11)所示。轨道实际控制参数如表4所示。
(11)

表4 轨道控制参数Table 4 Parameters of orbit control
在轨控时,卫星的定轨精度、执行机构的控制精度都会使半长轴控制产生误差,例如2-2卫星,半长轴控制存在5%的误差,卫星轨道高度实际控制降低量小于预期值,但仍满足星座构型维持需求。轨控后两星相对1-1卫星相位角差随时间逐渐减小,如图7所示,相位差变化率分别为0.016(°)/d和0.014(°)/d,轨道偏心率小于0.001,符合预期。根据轨道外推仿真和曲线拟合,星间相对相位差在未来的寿命期(一年)内可维持在±5°阈值内,不需要再进行相位维持,如图8所示,且星座中其他卫星在寿命期内相对基准卫星的相位漂移量也将维持在±5°阈值,不需要进行轨道维持。相对于星座绝对构型维持,卫星绝对相位角30 d就会漂移至5°阈值,即每个月要实施一次相位保持,大大降低了星座维持频次,提高卫星服务效率。
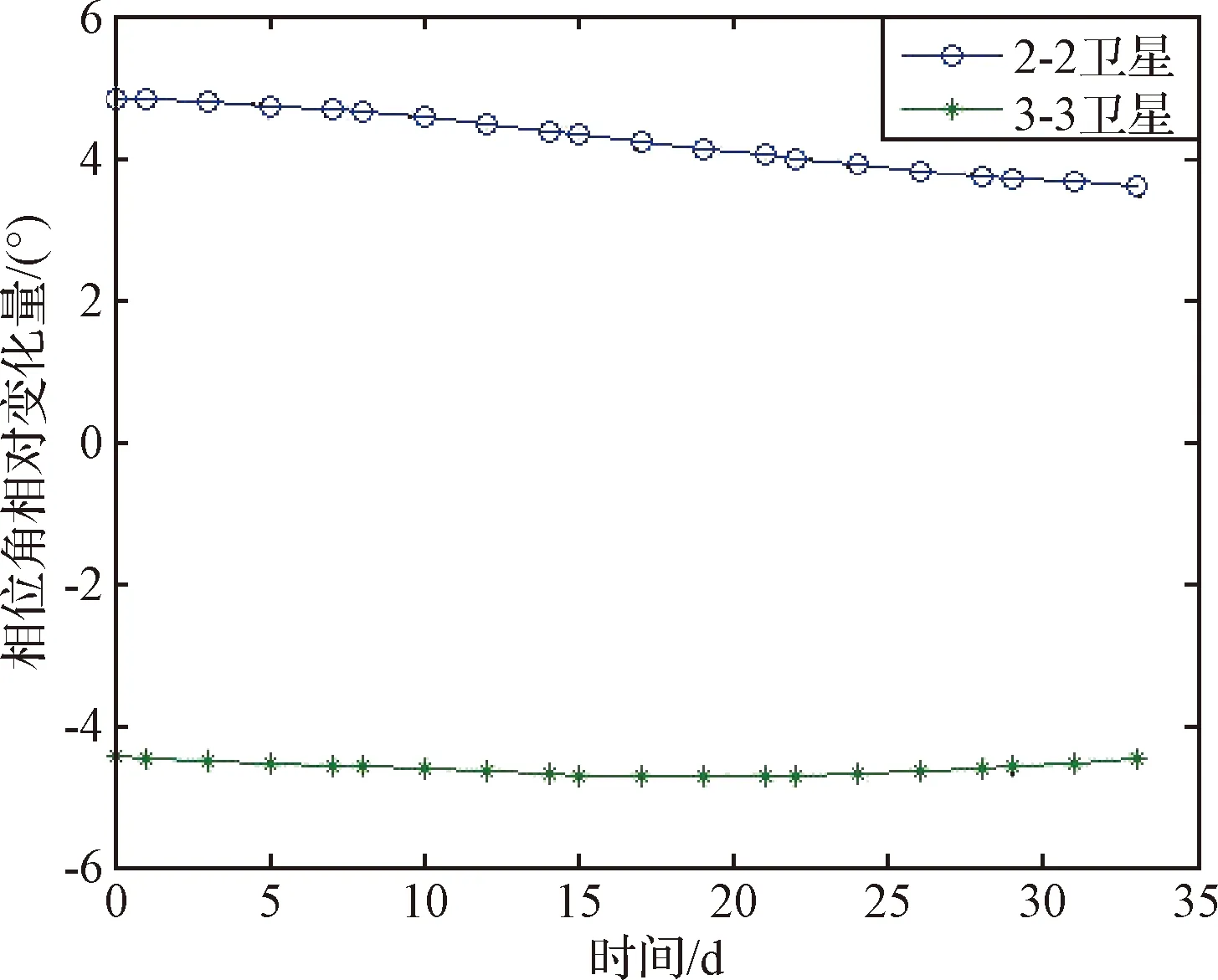
图7 轨控后相对基准星相位差变化情况Fig.7 Variation of relative phase after control
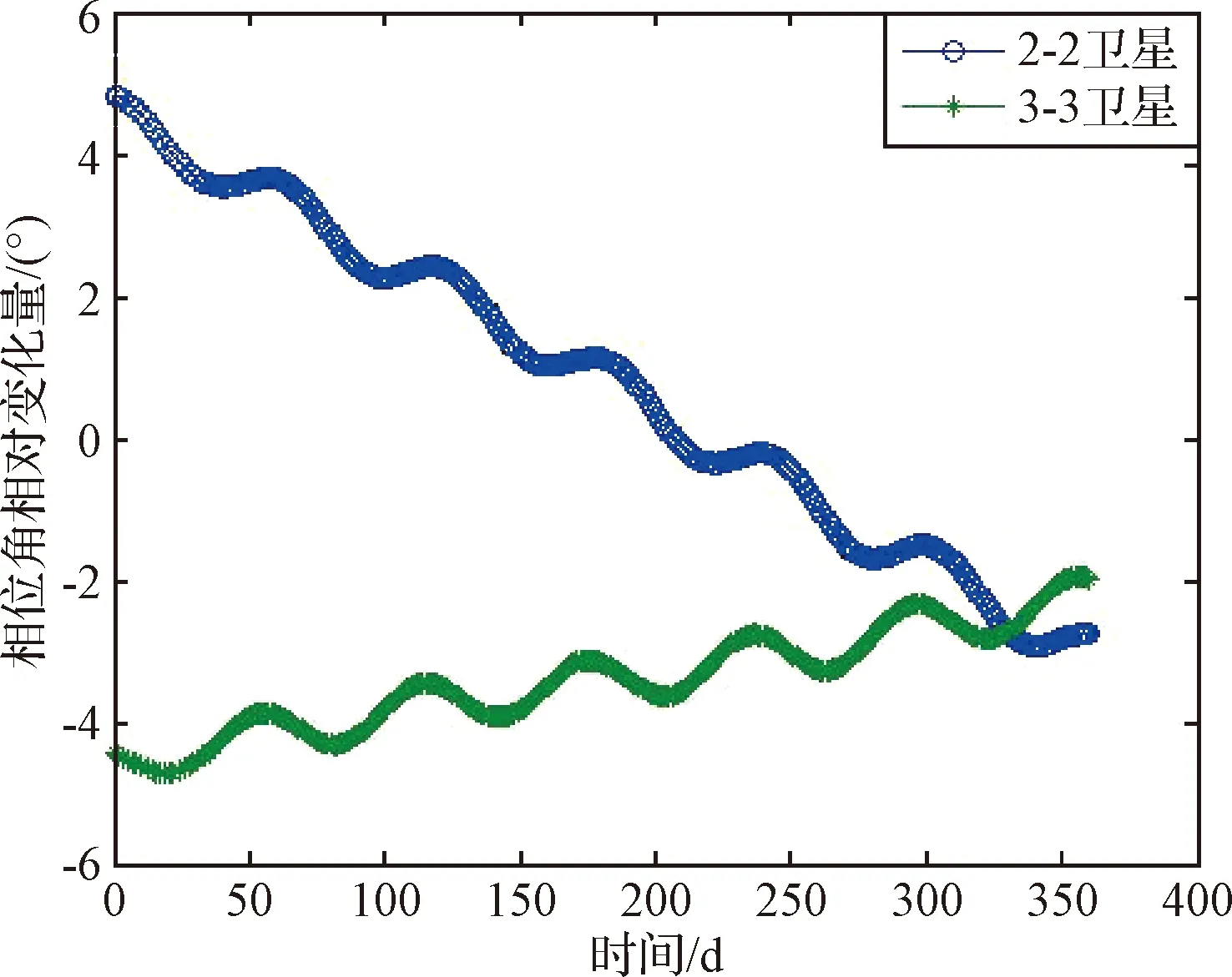
图8 卫星相对基准星相位角一年内变化量仿真值Fig.8 Simulation of relative phase in a year
本策略在进行相位调整时未将卫星相位调整至与标称相位差完全一致,而是通过一次轨道高度的抬升/降低使卫星的相位漂移方向相反,减小相位偏差,这样做不仅可以省略一次升轨/降轨控制,节约燃料,缩短轨控时长,减少因相位维持导致的任务中断时间,同时使卫星相位角在要求阈值范围内漂移,满足星座覆盖特性指标。
4 结 论
本文结合卫星星座实测轨道数据,分析了低轨卫星所受摄动力及其组成的Walker星座构型演化特点。结果表明:低轨Walker星座构型发散主要是由卫星初始轨道参数不一致引起,其中,轨道半长轴是星座构型漂移的最关键因素;半长轴偏差在20 m量级以内时,倾角的偏差及周期性变化使不同轨道面卫星的升交点赤经及相位角变化非线性,存在周期项;对于低轨卫星,初始轨道参数偏差对升交点赤经长期摄动影响很小,在星座构型维持时仅需考虑对卫星相位角的维持;某星座卫星由于受大气耗散力的作用使轨道半长轴发生衰减,但衰减量并不会影响星座的覆盖性能指标,因此,本文采用基于基准卫星的相对相位维持策略,只进行一次相对于基准星的轨道高度抬升或降低,改变卫星相对相位角的漂移方向,实现对星座构型的维持,经过实际工程应用验证,基于基准卫星的相对相位维持策略在星座的寿命期内只需进行两次轨道维持,消耗燃料0.0034 kg,相对于绝对构型维持,不仅大大降低构型维持频次,且缩短轨控时长,节约燃料,提升星座的服务性能。
