基于深度学习的组合体航天器模型预测控制

康国华，金晨迪，郭玉洁，乔思元

(南京航空航天大学航天学院，南京 210016)

0 引 言

近年来随着航天任务复杂度的提高，航天任务已经不再局限于单星或多星组网的对地观测、通信、导航等常规领域，空间维修、在轨加注、捕获等复杂操控技术等日益受到关注。国外已有航天公司计划未来运用卫星进行小行星捕获探测任务[1-2]。比如NASA的ARM任务计划捕获一颗近地轨道的小行星或者从一些较大的小行星上获取碎片，并将其运送至地月系统中。这类任务中新组合体的姿态控制问题是目前亟待解决的问题。

组合体在形成过程中，由于服务航天器和目标航天器之间角速度等状态的不匹配、惯量估计误差等会在组合瞬间带来未知大小的姿态扰动，组合体姿态紊乱，按照原有控制方式将无法稳定组合体姿态，甚至无法进行后续操作，需要寻求新的控制方式在模型精度存在误差下，使得组合体重新回到三轴稳定状态。

国内外学者针对组合体航天器的姿态控制已开展了较长时间的研究。文献[3]提出了一种基于动力学模型的自适应线性反馈控制方法，但其在仿真中只考虑了平面情况。文献[4]提出了一种非合作附着体的自适应控制，对多种附着情形下的稳定控制进行了仿真校验。文献[5]提出了两种基于角动量守恒的关节阻尼控制和关节函数参数化协调控制，但在仿真中假设条件比较理想：抓捕机构和目标航天器间的相对速度为零，目标相对于抓捕航天器的质量体积小，不考虑飞轮饱和等。文献[6]提出了一种自适应变结构控制算法，算法简单，辨识精度相对较高。文献[7]提出了一种基于机械臂耦合力矩评估的组合航天器姿态协调控制方法，文献[8-9]采用滑模变结构控制实现组合体姿态稳定，文献[10]提出了一种基于干扰观测器的有限时间控制策略，文献[11-13]对推力受限情况下的空间机器人与目标航天器形成的组合体的姿控进行研究。

上述算法虽都解决了一定场景下的组合体控制问题，但都是通过控制反馈(先控制再看结果)的模式，未能实现对多种控制目标的快速响应，即没有记忆性，难以满足未来复杂航天任务的要求。针对这一需求，本文将能有效处理耦合约束[14]的模型预测控制算法引入，该算法能够有效克服控制过程中的不确定性和非线性，方便操纵变量中的各种约束，已在工业生产中广泛应用[15-16]。但其二次规划求解过程需要较多的计算资源，在航天领域应用还需改进。鉴于深度学习算法在多参数寻优上的优势，可以将两者结合起来。通过前期的场景训练，实现在实际应用中的快速响应。随着航天器在轨操作次数增加，每次操作过程都会产生大量数据并遥测下传，该数据可为深度学习技术的在轨实现提供样本信息。目前工业生产中已对两种算法的结合进行了一定研究，如Ph中和过程预测，加热炉炉温预测等。

结合上述两种算法特性，本文提出了一种基于深度学习的模型预测算法，该方法通过模型预测控制对深度学习算法进行在线训练，完成当前场景训练后，可利用深度学习算法代替模型预测算法进行航天器姿态控制，从而实现低硬件需求下的智能控制。

1 航天器模型预测控制建模

模型预测控制是基于当前时刻的状态，通过计算接下来几个预测周期内的控制力矩，进而获取接下来几个周期内的预测值，其计算过程和时间关联紧密，需要对传统的航天器姿态动力学模型进行离散化修改，使控制力矩参与到角度更新。假设组合体为刚性连接，整个组合体为刚体对其动力学与运动学进行建模。

1.1 模型预测下的姿态动力学建模

假设组合体航天器的惯量参数已辨识。则航天器连续姿态动力学方程可写为：

(1)

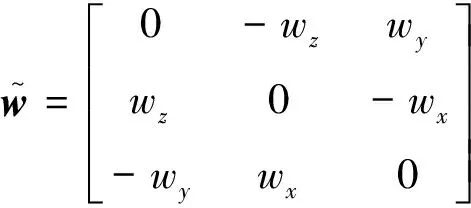
式(1)通过移项可得到关于角速度的微分方程：

(2)

式(2)即为常用的航天姿态动力学模型。对此模型进一步线性化，对式(2)右边项在任意(wr,Tr)处进行泰勒展开，只保留一次项，得到：

(3)

简化式(3)在(0,0)处展开：

(4)

式(4)仍是连续方程，上述方程时间量体现在角速度的变化，需要对其进行离散化处理，采用近似离散化，即：

(5)

式中：E为单位矩阵，t为航天器姿态控制周期。

结合式(5)，可将式(4)离散化为：

(6)

式(6)即为离散化后的航天器姿态动力学方程，可用于模型预测控制。

1.2 模型预测下的姿态运动学建模

以四元数方式表示航天器姿态运动，考虑存在角加速度：

(7)

I-1为航天器惯性张量的逆，T为控制力矩。

将式(7)进一步写为以下形式：

(8)

将式(8)中的A，B近似离散化：

(9)

式中：E为4×4单位矩阵，t为控制周期。

将式(9)代入式(8)可得离散化后用于模型预测的航天器姿态运动学模型：

I-1T(k))

(10)

式中：姿态四元数q可由姿态敏感器测量得到的航天器姿态角经公式转换获得。

2 基于深度学习的模型预测控制算法设计

2.1 控制算法总体设计

基于深度学习的模型预测算法以模型预测算法为前期控制算法，通过控制结果来在线训练深度学习网络。当完成该场景下的训练后，深度学习将完全代替模型预测算法实现对航天器姿态控制的接管。通过对场景库的不断丰富，可实现多场景下的快速姿态控制，算法整体流程图如图1所示。相比于传统智能算法，本方案加入深度学习网络场景库以增加算法的记忆性，即在对当前场景训练完成之后，将训练权值与目标存入对应数据库中，每次更新控制目标之后，优先通过查询数据库中已有场景进行匹配，加强算法对航天器的控制效率。

图1 基于深度学习的模型预测算法整体流程图Fig.1 Overall flow chart of model prediction algorithm based on deep learning

2.2 模型预测控制器设计

2.2.1模型预测方程

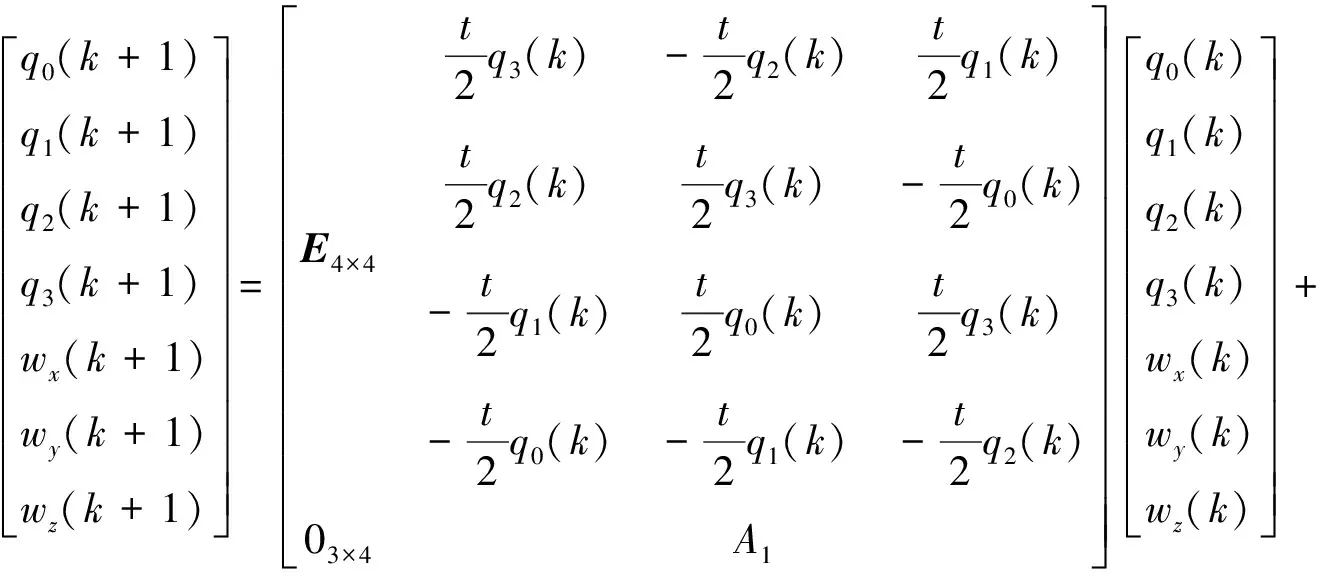
(11)

式中：k表示当前时刻，k+1为下一时刻，当前时刻的四元数和三轴角速度都可通过传感器测量得到，惯性张量I为已辨识完成的量，A1为3×4矩阵，计算公式同式(5)第一项。

为了简化公式表达，如无特殊说明，式(11)都将以如下形式出现：

x(k+1)=A(k,t)x(k)+B(k,t)T(k)

(12)

设定预测时域为N，预测时域内系统的状态量可由式(13)计算获得：

x(k+N|k)=AN(k,t|k)x(k|k)+

AN-1(k,t|k)B(k,t|k)T(k|k)+…+

A(k,t|k)B(k,t|k)T(k+N-2|k)+

B(k,t|k)T(k+N-1|k)

(13)

为了明确各量之间的关系，对系统未来时刻的输出状态量以矩阵的形式表达：

Y(k)=αx(k|k)+βμ(k)

(14)

式中：

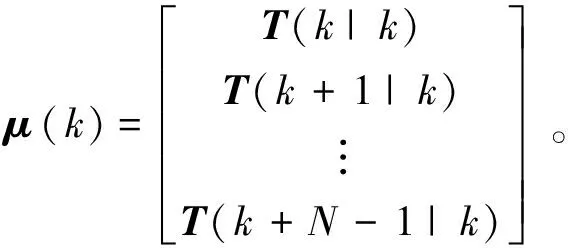
通过式(14)即可预测出时域N内每个控制周期的控制力矩和姿态。

2.2.2滚动优化

为了求解符合要求的最优控制量，需要设定合适的优化目标，论文采用如下目标函数：

ρ(k)=[Y(k)-Yref(k)]TQ[Y(k)-Yref(k)]+

uT(k)Ru(k)

(15)

式中：Yref为参考输出轨迹，Y(k)，u(k)定义与式(14)相同，Q为状态量权重对角矩阵，R为控制量权重对角矩阵。

整个目标函数的功能是使系统能够尽快且平稳的达到期望值，即希望控制时间最优，并且将控制量引入到目标函数，避免控制量跳变对系统性能的影响。

由式(14)可得：

(16)

将式(16)代入式(15)：

ρ(k)=[α(x(k|k)-xref(k|k))+βμ(k)]TQ·

[α(x(k|k)-xref(k|k))+βμ(k)]+

uT(k)Ru(k)

(17)

将式(17)经过矩阵运算，可写成二次规划形式：

(18)

式中：H(k)=2(βTQβ+R)，f(k)=2βTQα·[x(k|k)-xref(k|k)]，σ(k)={α[x(k|k)-xref(k|k)]}TQα[x(k|k)-xref(k|k)]。

对式(18)进行求解，即可解得在预测时域内一系列系统状态量与控制量，模型预测取第一个控制量作为实际控制量作用于系统输入，下一控制周期开始，预测时间同时向前推移，通过这种滚动优化实现最优时间的航天器姿态控制。

2.3 深度学习网络设计

针对不同控制目标和场景需要不同的控制参数，但在同一控制目标下，如果航天器模型参数未发生变化，其控制参数不变，所以论文采用卷积神经网络，利用其权值共享的优点，设计深度学习网络。

2.3.1卷积神经网络结构设计

(19)

式中：各四元数结构定义与式(7)相同。

qe0，qe1，qe2分别对应三轴方向矢量与旋转角度的正弦值的乘积，数值中已包含三轴方向和旋转角度信息，所以仅需对其控制参数进行训练，qe2为旋转角度余弦值，不需要额外加入至训练中。卷积神经网络结构如图2所示，针对三轴稳定控制需要用同一组误差四元数与三轴角速度计算出三轴控制力矩，所以卷积神经网络采用三组卷积核，分别对应计算三轴控制力矩。为了利用梯度下降法对卷积神经网络进行训练，需要对计算的三轴控制力矩需要进行激活，这里采用tanh函数，保留数据的正负特性。

图2 卷积神经网络结构Fig.2 Convolution neural network structure

2.3.2深度学习网络控制

利用第2.2节中的模型预测控制在每个控制周期中所计算的控制力矩作为输出样本，当前时刻组合航天器的姿态四元数与三轴角速度作为输入样本，进行在线训练。

当卷积神经网络的输出误差小于10-9可认为在该场景下完成卷积神经网络的训练。将该场景下的控制参数数据存入场景库，数据格式如表1所示。

表1 深度学习网络场景库格式Table 1 Library format of deep learning network

后续控制将优先查询场景库中的数据，如查询到当前场景已在前期进行训练完成并入库，则直接选用该组数据，利用卷积神经网络进行组合体姿态控制。如该场景并未入库，则匹配与期望目标最相近的场景作为训练输入，加快训练速度。

3 仿真校验和分析

3.1 仿真环境设置

为了对所提出的方法进行仿真分析校验，利用Matlab构建模型预测控制和深度学习神经网络，整个仿真运行环境如表2，3所示。

表2 仿真软硬件环境参数Table 2 Software and hardware environment for simulation

表3 组合航天器惯性参数Table 3 Inertial parameters of combined spacecraft

3.2 模型预测控制仿真分析

3.3 基于深度学习模型预测控制仿真分析

航天器初始状态设定、预期目标设定和模型预测控制程序设定与3.2节相同。设置卷积神经网络训练学习率为10，每次模型预测控制周期内都对该网络进行训练，设定当输出误差小于10-9时，网络训练已完成。当卷积神经网络在控制过程中误差大于10-4时，需重新启用模型预测控制，修正卷积神经网络的控制参数。

表4 姿态仿真结果统计表Table 4 Statistical results of attitude simulation

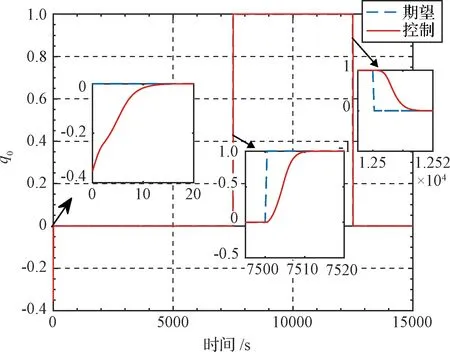
图3 四元数q0变化曲线Fig.3 The q0 curve

图4 四元数q3变化曲线Fig.4 The q3 curve

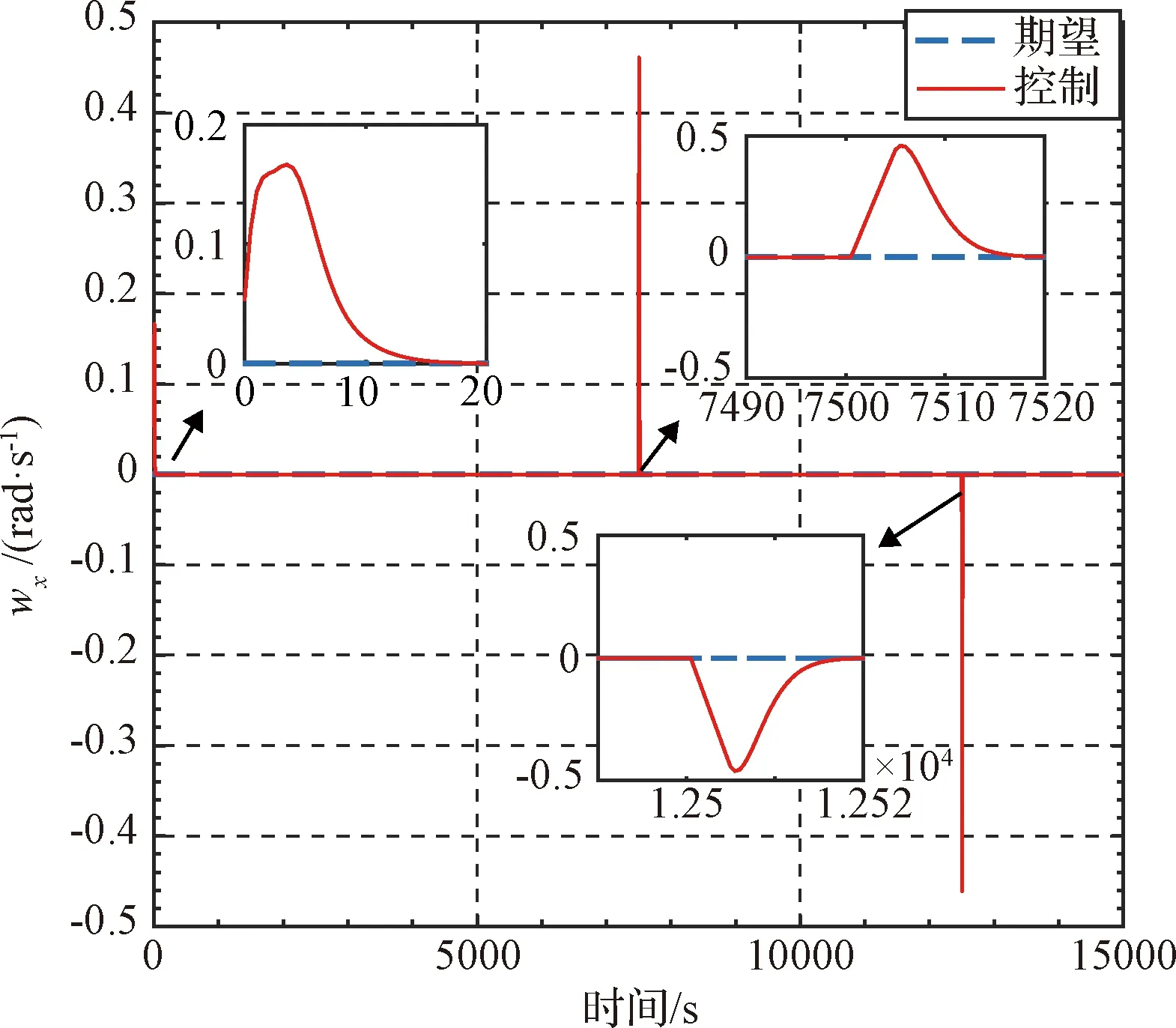
图5 x轴角速度变化曲线Fig.5 x axis angular velocity

图6 y轴角速度变化曲线Fig.6 y axis angular velocity

图7 z轴角速度变化曲线Fig.7 z axis angular velocity

表5 姿态仿真结果统计表Table 5 Statistical results of attitude simulation

图8 四元数q0变化曲线Fig.8 The q0 curve

图10 x轴角速度变化曲线Fig.10 x axis angular velocity

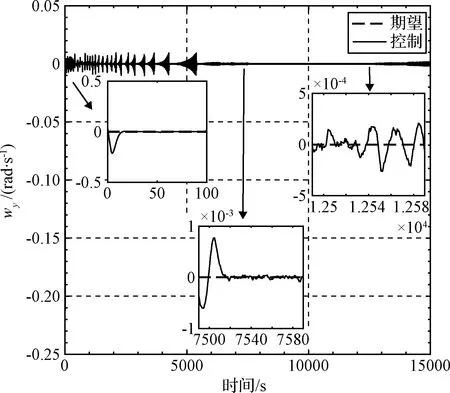
图11 y轴角速度变化曲线Fig.11 y axis angular velocity

图12 z轴角速度变化曲线Fig.12 z axis angular velocity

图13～15给出了深度学习网络在训练过程中的力矩输出量，实线部分为模型预测算法给出的控制力矩用于对深度学习网络训练，虚线部分为深度学习网络输出的控制力矩，从图中可以看出单次训练在20 s之内都可跟随上模型预测控制输出。对整体15000 s的仿真分析可知，在初次对深度学习网络进行训练后，当输出误差小于设定值时，实际深度学习网络控制参数并未训练至最优，需要后续多次模式切换来进一步训练深度学习网络，使深度学习网络达到一个收敛值。

上述整个控制过程的硬件计算时长为71.4 s，相比3.2节的仿真时长393.8 s缩短了约5倍。在算法上降低了对计算硬件的需求，节省了计算资源。

图13 x轴控制力矩曲线Fig.13 x axis control torque curve

图14 y轴控制力矩曲线Fig.14 y axis control torque curve

图15 z轴控制力矩变化曲线Fig.15 z axis control torque curve

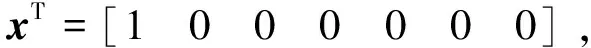
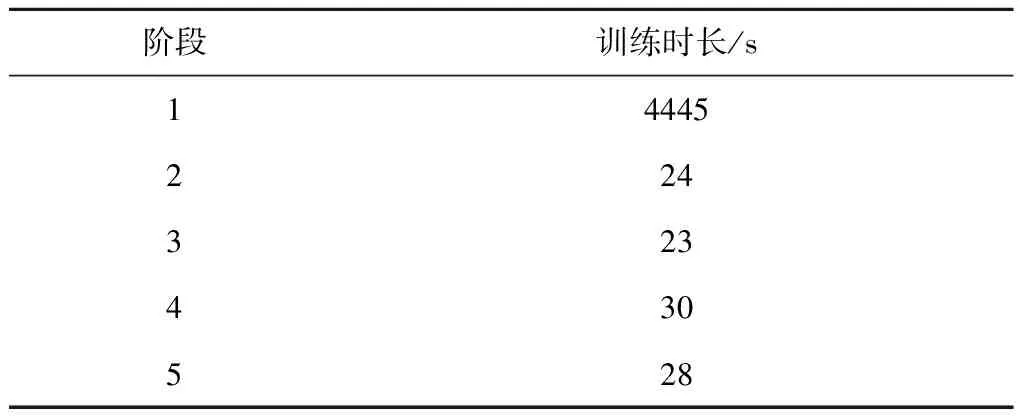
表6 场景切换深度学习网络训练用时统计表Table 6 Statistics time of deep learning network training

图16 多次期望四元数变化控制结果图Fig.16 Control results after changing desired quaternion

4 结 论

论文针对组合航天器在组合瞬间存在姿态扰动且组合后需要重新设计姿态控制率的问题，提出了一种基于深度学习的航天器模型预测控制方案。仿真分析表明，该方案在20 s内实现了对组合航天器姿态稳定的控制，控制精度在10-4量级。相比只依靠模型预测进行姿态控制，系统硬件消耗时间经统计由393.8 s降低至71.4 s，算法效率提高约5倍，表明该算法降低了对硬件要求，为依赖大量计算资源的模型预测控制运用于航天奠定了一定基础。此外，相比于传统的姿态控制算法和自适应等智能算法，论文提出的算法能够在大角度和角速度偏差下实现不同目标场景下的控制参数自主调节。通过建立场景数据库，控制参数能自主匹配，缩短了多任务场景下姿态稳定所需要的时间，在30 s内实现控制精度为10-4量级的控制效果。未来可通过丰富训练结果场景库，实现不同目标组合的快速姿态稳定控制。