《钉子板上的多边形》教学设计及思考

胡彩云

【教学内容】

苏教版五年级上册第108、109页。

【教学过程】

板块一、分类：钉子与图形

师：同学们，玩过钉子板吗？今天我们学习的是钉子板上的多边形，看来，研究的多边形要和钉子有关系呢。

师：一年级时我们就学过了分一分，明白分类可以按照不同的标准。（出示在钉子板上围好的多边形）它们可以怎么分类呢？四人小组里讨论一下。

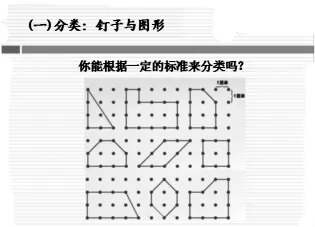
生：可以根据多边形的名称、轴对称图形、规则与不规则的图形、多边形边上的钉子数和内部的钉子数这些标准来分……

小结：同学们真爱动脑筋，想出了这么多的分类方法。我们先选取你们其中的一种标准，就按钉子板上多边形内部的钉子数来分类，抓住这样的要点来分类，对于我们探索活动或许会有帮助呢！

【设计意图：此板块中让学生将多边形分类，分类的标准不一样，方法就有很多，旨在打开学生的思路。分类后，又将视角直接指向根据“图形内部的钉子数”去分类，激发学生探索其中奥秘的兴趣。】

板块二、寻找：钉子与面积

选取内部钉子数是2的这类多边形来研究。

1.寻找规律。

师：（出示4个内部钉子数是2的多边形）这些钉子板上的多边形内部都有2个钉子，它们有什么不同呢？

生：边上的钉子数不同、面积不同、周长也不同。

师：多边形的面积和边上的钉子数之间有没有关系？又有怎样的关系？

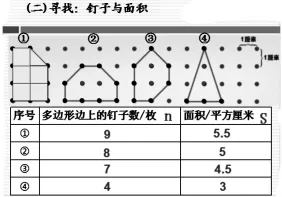
总结：钉子板上多边形的面积可以用算一算的方法，也可以用数一数的方法。

师：观察表格中的数据，面积数和边上的钉子数之间有没有关系呢？又有怎样的关系呢？把你的想法和小组内的同学交流一下。

生：我们小组发现面积数减去1，再乘2，正好是多边形边上的钉子数。

生：我们小组通过研究发现，当多边形的内部有两个钉子，多边形的面积数等于它边上的钉子数除以2加1。

总结：钉子数与面积数之间的关系。用S表示面积，用n表示多边形边上的钉子数，S=n÷2+1。

2.推理验证。

（1）教师举例。

师：我们再找几个例子来观察，多边形的面积数和钉子数符合这样的关系吗？

（2）学生自己举例子。

师：内部钉子数是2的多边形的例子举得完吗？能不能找到一个反例，证明这个规律不存在呢？同学们动手找一找，每人在点子图上画一个多边形，看看它的面积符合这样的规律吗？

【设计意图：教材是把“内部钉子数是1”的多边形作为例子开始研究的，我们慎重思考后，挖掘了教材的内涵，选择从“内部钉子数是2”的出发，思考有三：第一，这个规律比“内部钉子数是1”的稍难一些，教师引导、学生集思广益，更具有探讨价值。第二，内部钉子数是2的规律是S=n÷2+1，别小看了这个小尾巴“1”，它的规律形式更容易借鉴、归纳、推广。第三，我们的课堂只有40分钟，选择的事例要具有典型性、普适性和推广性。】

板块三、验证：钉子与发现

小组合作，开展探究活动。

师：内部钉子数不是2的多边形，它的面积数和边上的钉子数又具有怎样的关系呢？我们先来了解活动的要求。

看：观察多边形内部钉子数是几个。

数：数多边形边上的钉子数，算面积，并记录。

想：组长汇总数据，全组共同探索、寻找规律。

小组合作，学生分组活动。汇报。

总结：钉子板上围出的多边形的面积不仅和多边形边上的钉子数有关，还和多边形内的钉子数有关。

引导学生归纳，总结规律。

师：内部的钉子数是8，规律是什么？内部的钉子数是100呢？一个一个地写，写得完吗？

师：当内部的钉子数是a时，面积数和边上的钉子数关系是什么呢？

生：当内部的钉子数是a时，我们发现了规律：S=n÷2+（a-1）。

师：如果图形的内部没有钉子，面积数和边上的钉子数还符合这样的规律吗？你打算怎样验证呢？

师：每人画一个多边形，内部没有钉子，数一数边上的钉子数和面积数，看看符合规律吗？

总结：多边形边上的钉子数除以2加内部的钉子数减1的差，就是这个多边形的面积。这么复杂的关系我们用一个含有字母的式子清晰地表达出来了。

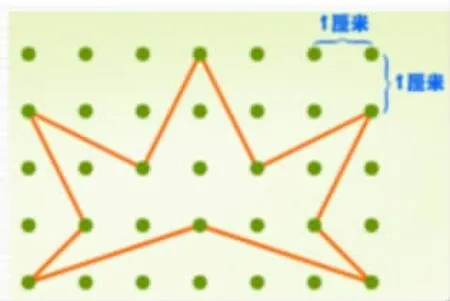
师：同学们看看这幅图，它的面积你能很快地告诉我们吗？

生：S=10÷2+（6-1）=10，它的面积是10平方厘米。

【设计意图：此板块我们做了三点尝试：一是准备已经画好了多边形的作业纸，把时间集中于探究规律的活动中。二是小组间探究内部钉子数不同的多边形的规律，交流展示发现的规律，提高了课堂探究的效率。三是学生通过不完全归纳法，发现规律，学生的探究不局限在知识层面，而是活动经验的积累、推广和应用，数学思想方法的渗透，学生在此过程中获得了多方面的提高。】

板块四、再猜：钉子与其他

师：刚刚我们研究的都是面积数和钉子数之间的关系，难道钉子数仅仅和面积数有关系吗？如果不止这些，还有什么呢？和小组里的同学交流一下你的想法。

生：我觉得钉子数可能与边数有关系。

生：我觉得钉子数可能与周长有关系。

生：我觉得当钉子数一定时，多边形面积最大是多少，最小是多少，会不会有规律呢……

小结：提出问题往往比解决问题更重要。再猜，为我们打开了思维的天窗。

【设计意图：跳出钉子数与面积的局限，留给学生足够的思考空间，触发学生用智慧去创新。】

【教学思考】

这节课以前怎么教

很多教师在设计《钉子板上的多边形》这节课时，往往都是直接出示点子图，提出猜想：钉子板上多边形的面积和什么有关系？进而提出问题：钉子板上多边形的面积和边上的钉子数以及内部的钉子数存在怎样的关系？接着从最简单的“内部钉子数是1”的多边形开始研究，用S表示面积，n表示多边形边上的钉子数，得到S=n÷2的规律；然后出示不符合此规律的多边形，明确钉子板上多边形的面积还和内部的钉子数有关系。先同桌合作，探究内部钉子数是2的规律；再采取小组合作模式，每人画一个内部钉子数是3或是4的规律；最后，用含有字母的式子表示规律。

按照这样的模式上课，会存在以下弊端：一是教师引导痕迹过重，学生探究活动比较被动。二是先探究内部钉子数是1，接着探究内部钉子数是2，再到其他，这样琐碎且重复的环节设计造成课堂模式的单一和时间的紧张。三是对于学生数学思想方法的指导和创新意识的培养有所欠缺。

智慧数学课堂的思考

“智慧数学”的课堂，我们把教学内容分为四个板块，板块一：“分类：钉子与图形”，通过问题迅速聚焦研究的角度，激发学生探索奥秘的兴趣。板块二：“寻找：钉子与面积”，直接从内部钉子数是2的开始研究，小组合作探究内部钉子数是 1、3、4、5 的情况，调整了研究的顺序，整合了课堂探究的环节，充足的合作时间保障了学生活动经验的累积。板块三：“验证：钉子与发现”，凭借推理，学生发现、归纳、总结了规律，掌握了不完全归纳法在探究规律时的运用。板块四：“再猜：钉子与其他”跳出了钉子数与面积的局限，开阔了学生的思路，促进学生的思维发展。