爆轰与聚能射流下射孔枪和套管的应力强度耦合仿真分析
2019-11-28曹银萍李明飞窦益华于洋
曹银萍 李明飞 窦益华 于洋
西安石油大学
0 引言
大孔径、高孔密、深穿透射孔是目前射孔工艺的发展方向,它将增加射孔弹的装药密度、装药量与爆轰能量,加剧对套管和射孔枪的损伤。国内西部油田和美国 Fort Worth 盆地[1]、Arkoma 盆地[2]以及墨西哥湾[3]等油田都曾遇到过射孔事故。射孔是包含能量、质量、速度及其变形转化的复杂动态过程,如何查明之间复杂的转换、转化和相互影响规律,如何实现真正意义的爆轰冲击下液固相变转化和流固耦合,为射孔枪和套管强度安全性分析提供依据是亟待解决的关键问题。
针对聚能射流对射孔枪的动态伤害,部分文献给出了数值分析结果,文献[4]应用开孔弹塑性力学理论,建立了射孔套管单孔应力分布模型,推导了应力集中系数,得到了整个圆孔周围应力分布规律。文献[5]采用ALE (Arbitrary Lagrange-Euler)法,模拟了射流形成过程及其对混凝土靶板的侵彻,分析了药型罩锥角对射流形成和侵彻的影响,未考虑对套管、射孔枪毛刺及其应力和强度的影响。文献[6-7]应用二维有限元法,分析了爆轰波叠加及干扰对偏转角的影响。文献[8-9]研究了ALE 算法在相关领域的应用,给出了研究方法和技巧,为进一步研究提供了借鉴和参考。文献[10]研究了非稳态喷射流通过射孔孔眼对套管强度的影响。文献[11]通过炸药做功和猛度实验,验证了爆轰波碰撞的聚能效果。文献[12]采用有限元和自适应网格技术,分析了射流和碎片撞击射孔枪壁的过程,分析了药型罩上附金属对胀枪高度的影响。
目前针对爆轰波冲击、叠加对能量和射流速度及套管强度的影响研究较少。文献[13]结合室内材料试验及有限元法,分析了承受非均匀载荷套管的力学性能。文献[14]应用SPH(Smoothed Particle Hydrodynamics)法,建立了不同药型罩射流模型,考察了不同药型罩材料形成金属射流的过程、速度、性质等。文献[15]利用LS-DYNA 软件,模拟了不同装药类型的聚能射流成型及侵彻过程,分析了对均质装甲钢的侵彻。文献[16]采用AUTODYNA 软件,模拟了Y1201 射孔弹压垮药型罩和侵彻套管的过程。文献[17]基于Hamilton 原理,建立一个包含射流强度、应变率效应、剪切、表面张力、动力学黏性和速度梯度等多耦合的金属射流运动方程。文献[18]应用ALE 法,对聚能装药在不同起爆方式下的射流形成过程进行了三维数值分析。
综上所述,目前针对爆轰波冲击、叠加对射孔枪和套管强度的影响研究较少。常用高速柱状体代替金属射流,未模拟爆炸和射流过程。侵彻是具有长度的一段金属射流,具有连续和持续性,简单用柱状体代替射流存在差异,影响分析精度。部分研究为二维建模,往往忽略射孔枪和盲孔的存在,而射孔枪盲孔将消耗掉一部分射流能量,并且二维模型无法模拟射孔弹间的互相干扰和影响。还有部分研究直接给出爆轰过程的关键参数,没有模拟真实爆轰,参数与实际情况匹配性差,同时也无法分析爆轰瞬间各部分间的能量分配。军工和火工主要针对武器和矿、煤开采等方面,工况、初始和边界条件与本次研究的初始高温和高压存在很大区别。为了分析爆轰波叠加对能量和射流速度及套管和射孔枪强度的影响规律,研究应用ALE 方法,建立射孔弹-射孔枪(盲孔)-套管三维有限元模型,实现爆轰过程、药型罩固流转化、射流侵彻套管的大变形和流固耦合仿真,提高分析精度,为射孔枪安全优化设计和爆轰冲击下套管的力学性能分析提供思路。
1 有限元建模及动态仿真过程
应用LS-DYNA 软件的ALE 方法,建立射孔弹-射孔枪-套管三维有限元模型,具体参数见表1。模型中炸药和药型罩之间,药型罩、射孔枪、套管与气体之间的接触采用Surface to Surf 和Eroding (ESTS),即侵彻接触类型。由于药型罩在炸药作用下形成聚能射流,在侵彻射孔枪和套管的过程中存在大变形和高速流动,采用Lagrange 算法会出现单元畸变的现象,而Euler 算法为了精确捕捉固体材料的变形响应需要很精细的网络,极大增加了数值分析的成本。ALE 算法(Arbitrary Lagrange-Euler)则可以很好地解决大变形和流固耦合问题。因此,空气、炸药、药型罩的单元算法为ALE 算法,空腔、套管、射孔枪采用Lagrange 单元算法。
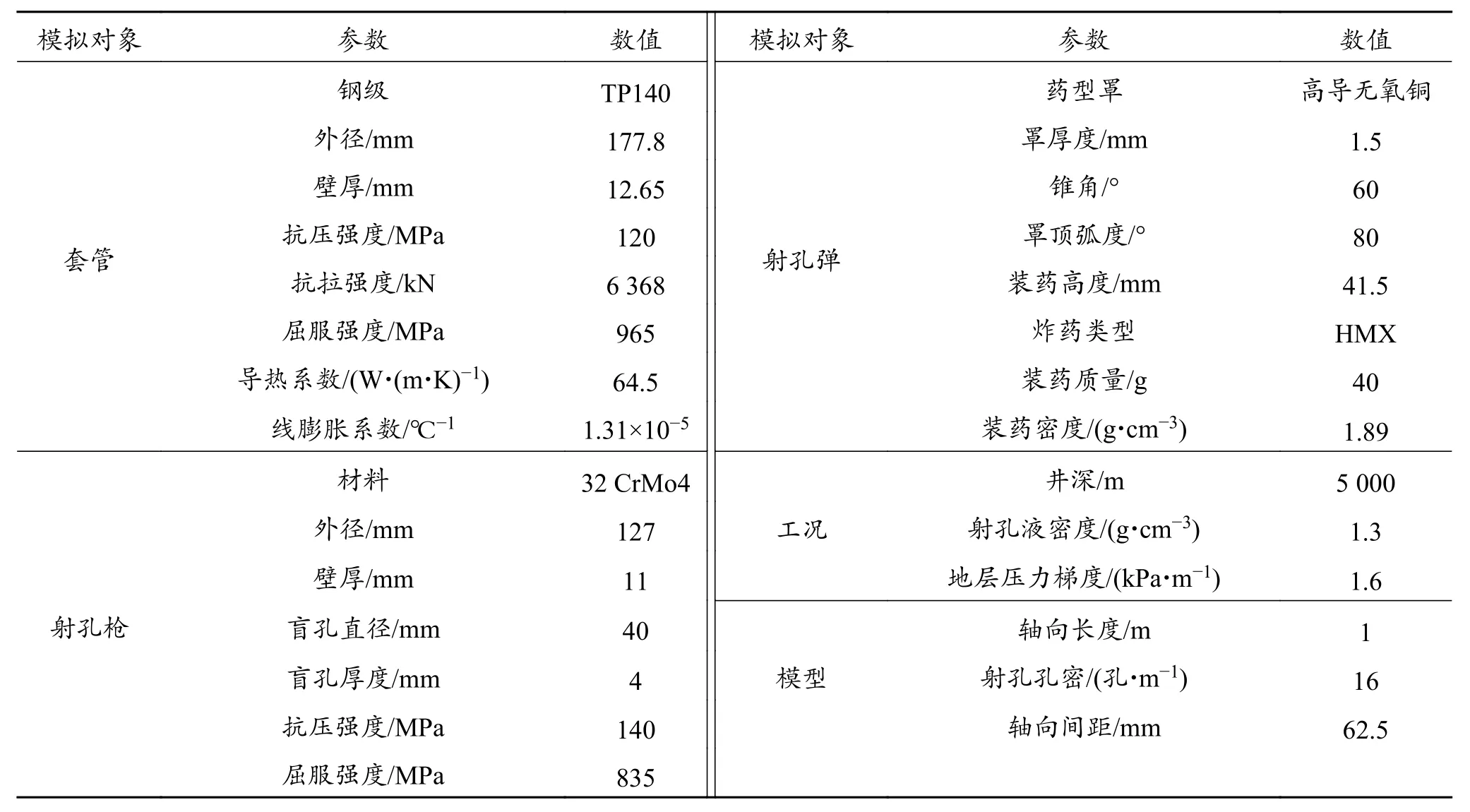
表1 有限元建模关键参数Table 1 Key parameters of finite element modeling
为了在确保得到准确模拟结果的同时尽量缩短计算时间,需要控制单元大小和总数。为此,细化了射孔弹及其周围的模型。首先,在粗网格上采用Oseen 迭代法求解非线性问题;然后,在细网格上分别并行求解Oseen、Newton、Stokes 线性问题以校正粗网格解,对于空间变量采用有限元离散,时间变量采用向后Euler 格式离散。所建单枚射孔弹系统有限元模型中共有1 545 678 个节点,1 465 987 个单元。如图1 和图2 所示为单枚和3 枚射孔弹起爆、压垮、射流、侵彻射孔枪和套管的全过程。爆轰给药型罩施加高温高压,形成抛掷,在轴线上激烈碰撞,形成细束金属射流和密实完整的杵体,速度梯度使得射流被拉长,最终断裂成局部杵体。LS-DYNA软件的ALE 方法是近期分析爆轰和超高速撞击、侵彻的一个新方法,文献[5-7]已经初步验证了该方法的可行性,笔者目前在进行2 级氢气炮加速药型罩弹丸至7 000 m/s 的侵彻套管、水泥环、围岩板靶实验,将进一步验证该方法的可行性和可靠性。

图1 单枚射孔弹射孔动态过程Fig.1 Perforating behavior process of one perforating charge
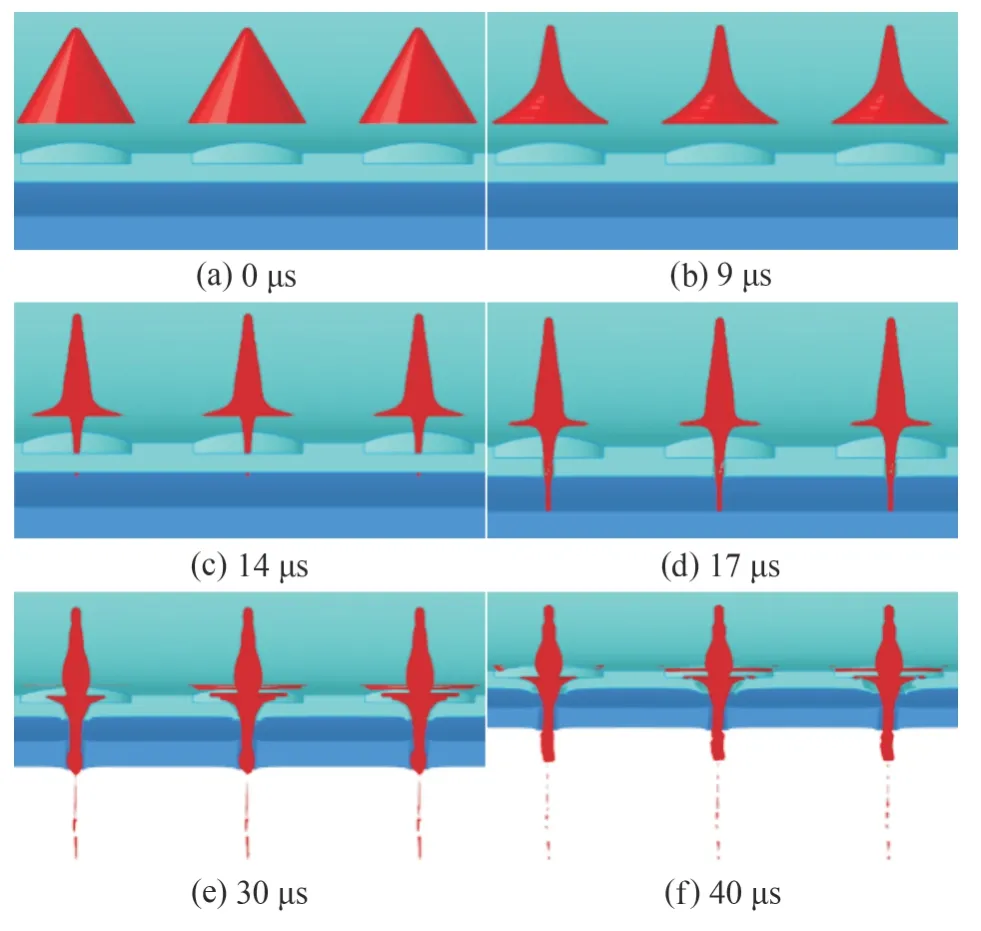
图2 3 枚射孔弹射孔动态过程Fig.2 Perforating behavior process of three perforating charges
2 ALE 描述下聚能射流和流固耦合动力学方程的建立
基于ALE 聚能射流和流体化的射孔枪盲孔材料动力学方程,可在Euler 描述下流体动力学方程基础上推导得到。ALE 描述与Euler 描述的本质区别是材料时间导数项的不一致。
2.1 连续性方程
在Euler 描述中,聚能射流和流体化的射孔枪盲孔材料连续性方程,即质量守恒方程为
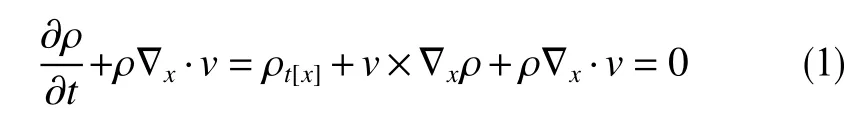
式中, ρ为流体密度,kg/m3;x为 Euler 坐标系下流体的坐标,m; ∇x·为 空间散度;v为流体速度,m/s; ρt[x]为流体坐标x固定时,对材料密度求时间的导数; ∇x为空间梯度。
将流体时间导数表达为固定坐标下ALE 对时间的偏导数和空间梯度的形式为
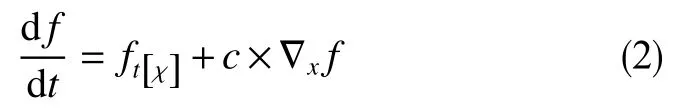
式中,f为场函数;t[χ]为 流体时间,s; χ为ALE 坐标系下流体的坐标,m;c为爆炸产物中的声速,m/s。
应用ALE 材料时间导数(2)式替换(1)式中的材料时间导数项,可得ALE 下的连续性方程为

2.2 动量守恒方程
Euler 描述中,流体化的射孔枪盲孔材料动量守恒方程为

式中,vt[x]为流体坐标x固定时,对流体速度求时间的导数; σ为应力张量;b为单位质量体力向量。同理,用(2)式替换(4)式中的材料时间导数项,可得ALE 描述下的动量守恒方程为
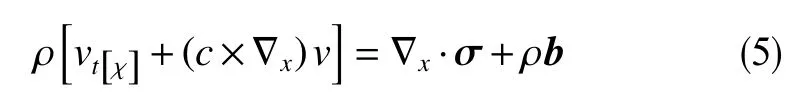
2.3 能量守恒方程
Euler 描述中,流体化的射孔枪材料能量守恒方程为

式中,e为单位质量内能,J/kg;et[x]为流体坐标x固定时,对单位质量内能求时间的导数;D为变形率;q为单位面积热流矢量,W/m2;ρs为单位体积内的热源,W/m3。
应用(2)式替换(6)式中的材料时间导数项,可得ALE 描述下的能量守恒方程为

2.4 ALE 描述下流固耦合动力学方程
网格运动是通过控制网格运动的速度v1或控制参考流体运动的速度w来实现。参考材料速度为

式中,v1为网格运动速度,m/s;w为流体运动速度,m/s;X为Lagrange 坐标系下流体的坐标; χ(X,t)为某时刻流体坐标X固定情况下的流体坐标; χt[X]为流体坐标X固定时,对流体坐标求时间的导数。
由式(8)、(9),可得到ALE 描述下流固耦合动力学方程为

所以通过控制w可以达到控制v1的目的。应用LS-DYNA 软件,结合ALE 算法的内核,即可实现爆轰过程、药型罩固流转化、射流高速侵彻射孔枪和套管的大变形和流固耦合仿真。
3 射孔枪与套管的开坑、扩孔过程及孔径变化规律
在数值分析过程中,记录了不同时刻射孔枪与套管的开坑、扩孔过程,孔径变化过程,并分析了孔径变化的规律。
3.1 射孔枪开坑、扩孔过程及孔径变化规律
如图3 所示,13 μs 时金属射流头部接触射孔枪盲孔内壁,14 μs 时射流头部到达盲孔外壁。14~16 μs处于开坑阶段,孔眼直径为3.2 mm。射穿射孔枪后,后继射流持续侵彻射孔枪,35 μs 时,尾部通过射孔枪外壁。16~35 μs 处于扩孔阶段,孔眼直径由4 mm迅速增大到13 mm。因杵体尾部扫过射孔枪内壁,孔径由17.1 mm 增大到24.4 mm,平均孔径为18.7 mm。
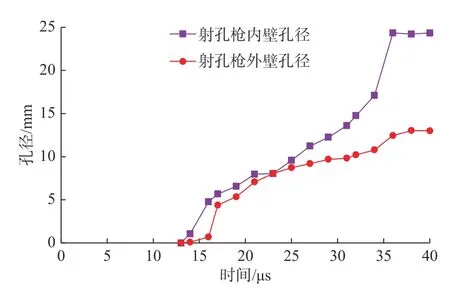
图3 射孔枪内外壁孔径变化规律Fig.3 Variation law of the perforation diameter in the inner and outer wall of perforating gun
3.2 套管开坑、扩孔过程及孔径变化规律
如图4 所示,15 μs 时射流开始接触套管内壁,23 μs 时射流到达套管外壁并穿透套管。15~23 μs为开坑阶段,孔眼直径达到3 mm。后续射流持续侵彻套管,30 μs 时尾部通过套管外壁,侵彻结束。23~30 μs 为扩孔阶段,套管外壁孔径由 3 mm 迅速增到7.8 mm,内壁孔径7.6 mm,平均孔径7.7 mm。对比图3 和图4 可知,杵体对套管孔径和孔道形态影响较大,造成内壁孔径增大,形成凹坑。射流穿透射孔枪后能量衰减明显,使套管较射孔枪孔眼直径小11 mm。
4 爆轰波叠加对射孔枪动态应力影响规律
4.1 单枚射孔弹射孔时射孔枪应力变化规律
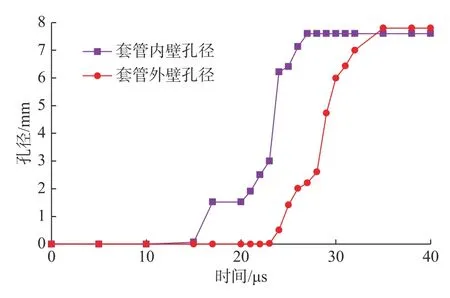
图4 套管内外壁孔径变化规律Fig.4 Variation law of the perforation diameter in inner and outer wall of casing
如图5(a)所示,13 μs 时射流头部接触射孔枪,射孔枪最大应力达到1.055 GPa;如图5(b)所示,14 μs时射流头部到达射孔枪外壁,应力最大值1.084 GPa;40 μs 时射流完全侵彻射孔枪,孔眼的周围有圆环状应力等值分布,最大应力不变。
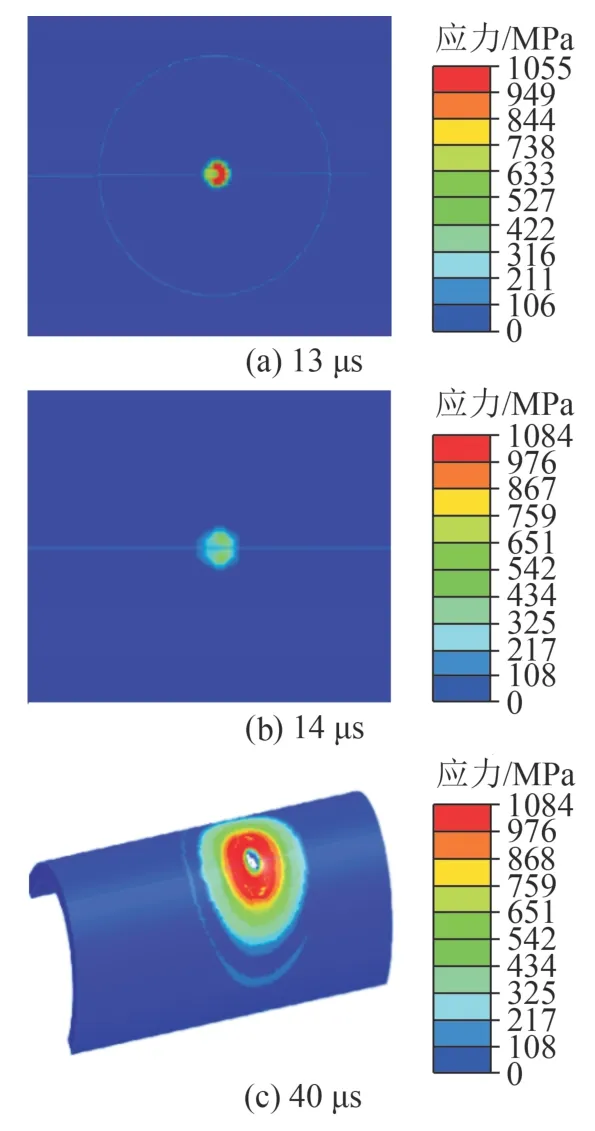
图5 单颗射孔弹射孔时射孔枪应力云图Fig.5 Stress cloud map of the perforating gun during the perforation of one perforating charge
图6 记录了射孔枪孔眼近似径向8 个点的应力值,距孔边距离22 mm 内点的应力均超过了材料屈服极限835 MPa,距离30 mm 内点的应力值也达到500 MPa,距离58 mm 内点的应力值接近0。距孔边距离0~22 mm 范围内射孔枪的材料类似于产生了“冷作硬化”现象,该区域内的材料不再符合原材料的应力应变规则,材料强度会略有提高,但韧性降低,材料变脆,沿着卸载曲线变化。

图6 单颗射孔弹射孔时射孔枪最大应力变化规律Fig.6 Variation law of the maximum stress of the perforating gun during the perforation of one perforating charge
4.2 3 枚弹爆轰波冲击和叠加对射孔枪动态应力影响规律
如图7(a)所示,13 μs 时射流侵彻射孔枪,应力瞬间增大。如图7(b)所示,14 μs 时射流头部到达射孔枪外壁,应力最大值达到1 084 MPa;截至此时,应力变化与单枚射孔弹时一致。如图7(c)所示,21 μs 时孔眼附近的高应力区持续扩展,还未叠加。如图7(d)所示,40 μs 时高应力区范围叠加、重合,应力增大;在三孔相连的长200 mm,宽125 mm 的宽带范围内,其最小应力也达到了774 MPa,接近材料的屈服强度;在高爆轰压力的作用下,该宽带会产生向外的鼓胀,即会发生所谓的“胀枪”。
如图8 所示,3 枚射孔弹射孔时,孔边最大应力达到1 076 MPa,与单枚时基本相符;距离孔边15 mm以外,单枚射孔的射孔枪应力急剧降低;3 枚射孔的射孔枪应力增加,在爆轰重叠中心,射孔枪应力达到996 MPa,较单枚时的878 MPa 提高了118 MPa。
5 套管应力变化规律分析
射孔弹爆轰瞬间,高温高压高速的金属射流会侵彻、损伤套管,影响后续工况射孔段套管的强度安全。
5.1 单枚射孔弹时套管的应力变化规律分析
如图9(a)所示,17 μs 时射流开始侵彻套管,套管内壁与射流接触区瞬间产生1.04 GPa 应力。如图9(b)所示,17 μs 时套管外壁和除接触点外的大部区域应力为0;继续侵彻、开孔,30 μs 时射穿套管。如图9(c)所示,30~40 μs 之间属于射穿套管后的扩孔阶段。套管外壁受射流影响区域进一步扩展,直至如图9(d)所示,侵彻套管结束时,距孔边缘10 mm范围内环形区域内应力可以达到1.27 GPa,其边缘应力也达到了965 MPa,超过了TP140 套管的屈服极限,相当于产生了“冷作硬化”,射孔结束后该区域内的材料不再遵循原材料的应力应变规则,屈服强度将略有提高,对套管强度的影响有待进一步研究。
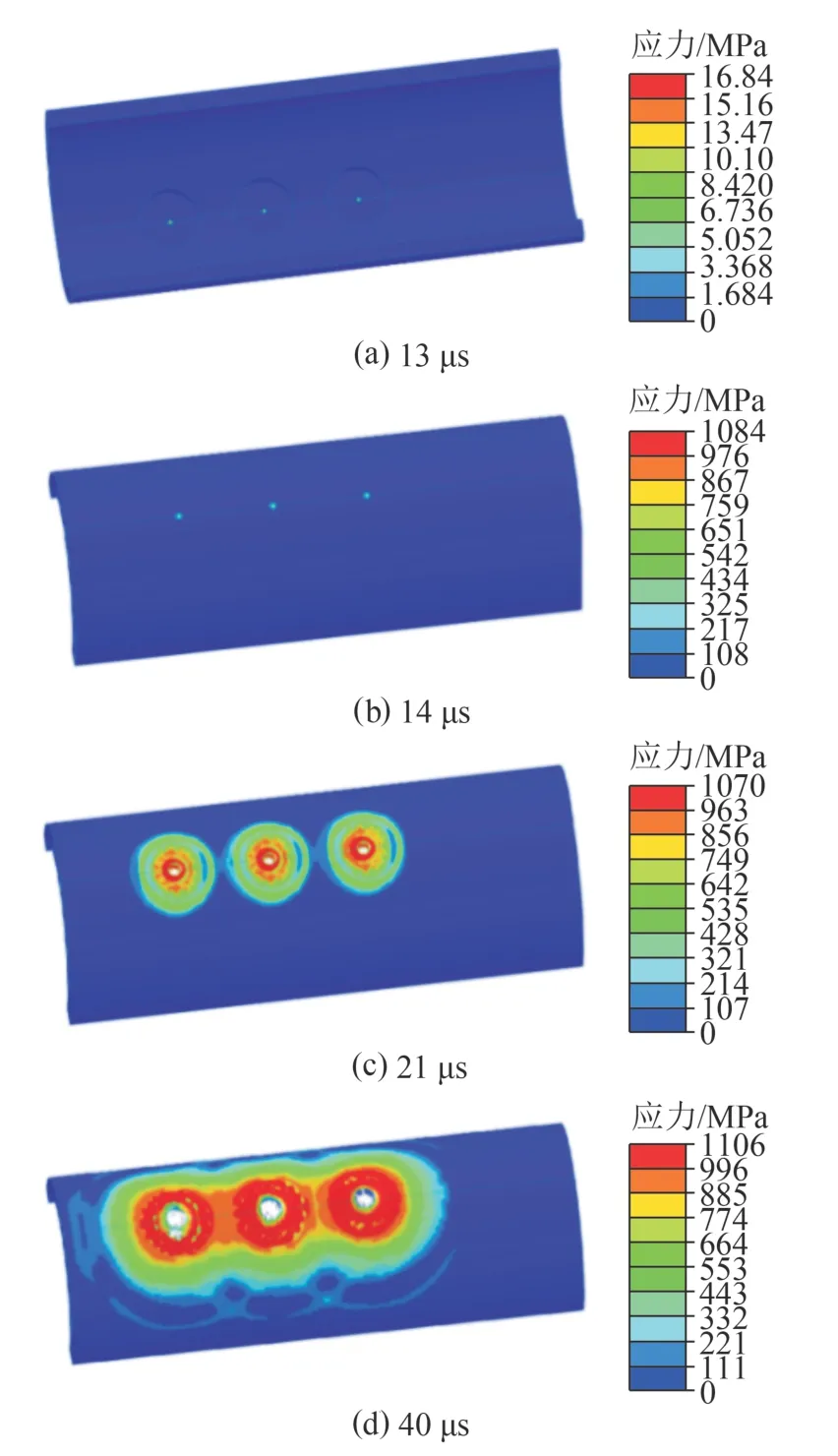
图7 3 颗射孔弹射孔时射孔枪应力云图Fig.7 Stress cloud map of the perforating gun during the perforation of three perforating charges

图8 单枚和3 枚射孔弹射孔时套管应力变化曲线Fig.8 Variation of the casing stress during the perforation of one perforating charge and three perforating charges
由图9(d)可知,40 μs 时套管上仍然存在应力超过965 MPa 的危险区域,因此记录并考察了套管孔眼径向上与孔眼不同距离的12 个点的应力变化情况。如图10 所示,距孔边10 mm 内所有点的应力均超过套管材料的屈服强度;在距离孔眼0~8.3 mm范围内,计算点的最大应力降低相对缓慢,但是在8.3 mm 以后,测量点的应力迅速下降;距离孔边越近,其应力值落在屈服极限上方的范围越大。
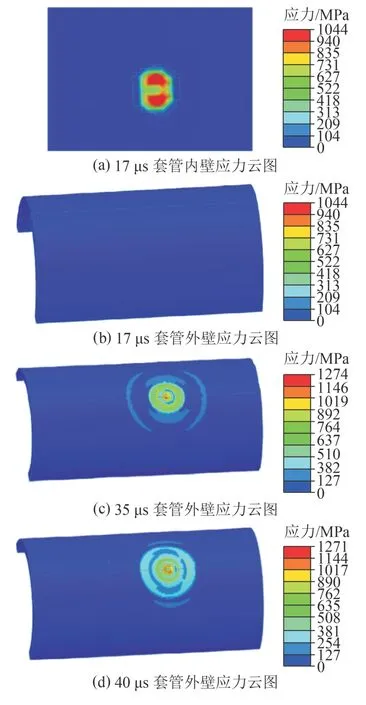
图9 单枚射孔弹套管应力云图Fig.9 Stress cloud map of the casing during the perforation of one perforating charge
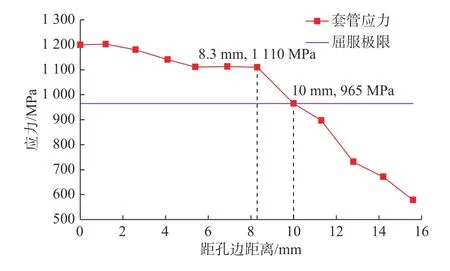
图10 套管最大应力变化规律Fig.10 Variation law of the maximum casing stress
5.2 弹间相互作用对套管应力变化的影响
如图11 所示,3 枚射孔弹爆轰不同时段套管的应力云图。16 μs 时金属射流接触套管内壁,较单枚射孔弹提前了 1 μs;22 μs 时射穿套管,较单枚射孔弹提前了8 μs,此时孔眼处最大应力达到1.30 GPa,较单枚射孔弹增加了 0.26 Gpa;27 μs 时,应力变化区域的圆环开始相切,说明此时应力变化范围边缘距孔边距离为21.3 mm。随后应力变化区域继续扩展、互相重叠,如图11(d)所示,重叠区域的应力值较非重叠部分有所提高。
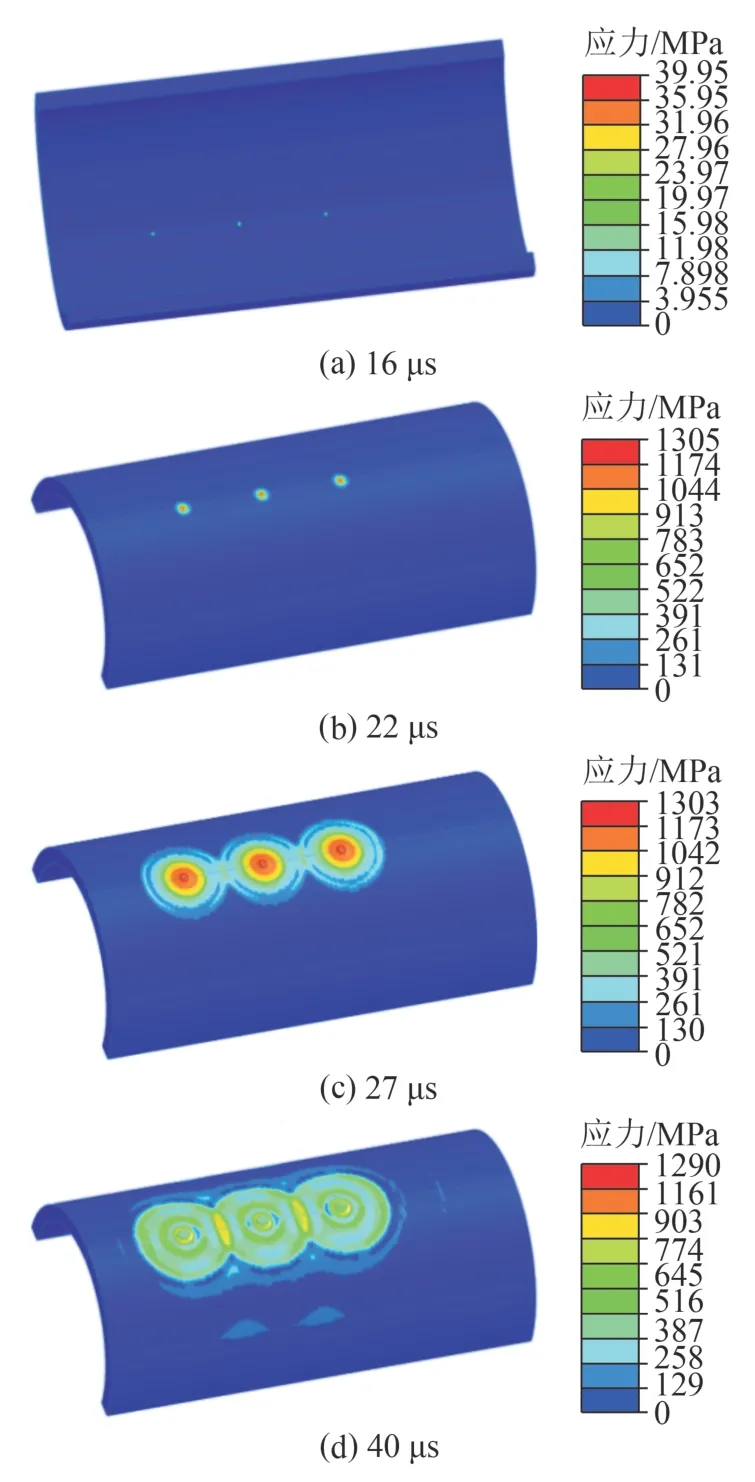
图11 3 枚射孔弹射孔时套管应力变化云图Fig.11 Stress cloud map of the casing during the perforation of three perforating charges
为考察两孔间套管应力的变化规律,针对两孔间连线上的13 个点的应力值开展研究。如图12 所示,孔距(两孔连线中点)在12.5 mm 范围内,其应力值均超过材料屈服强度965 MPa,较单枚射孔弹的范围扩大了2.5 mm 宽度的圆环;孔距在12.5~15.3 mm 之间,套管应力随孔距增加迅速降低。因射孔弹间干扰导致应力变化区重叠,孔距在15.3~21.3 mm 范围内,套管应力呈增加趋势,最大应力达965 MPa。因应力增加又泄压,15.3~21.3 mm 的重叠区域的力学属性将发生变化,强度会略有提高,但韧性降低,材料变脆,将影响套管的强度安全。

图12 套管相邻两孔间应力变化曲线Fig.12 Variation curve of the stress between two adjacent perforations in the casing
如图13 所示单枚和3 枚射孔弹射孔时套管应力变化对比曲线。3 枚射孔弹射孔套管的最大应力为1 273 MPa,比单枚时的1 207 MPa 略高;距离孔边大于8 mm,单枚射孔弹射孔的套管应力衰减速度明显大于3 枚时套管应力衰减速度;单枚射孔弹射孔套管应力持续减少,3 枚时套管在距离孔边超过15.3 mm 以上时,套管应力增加。在爆轰重叠区域中心,套管应力为965 MPa,较单枚时的226 MPa提高了737 MPa。
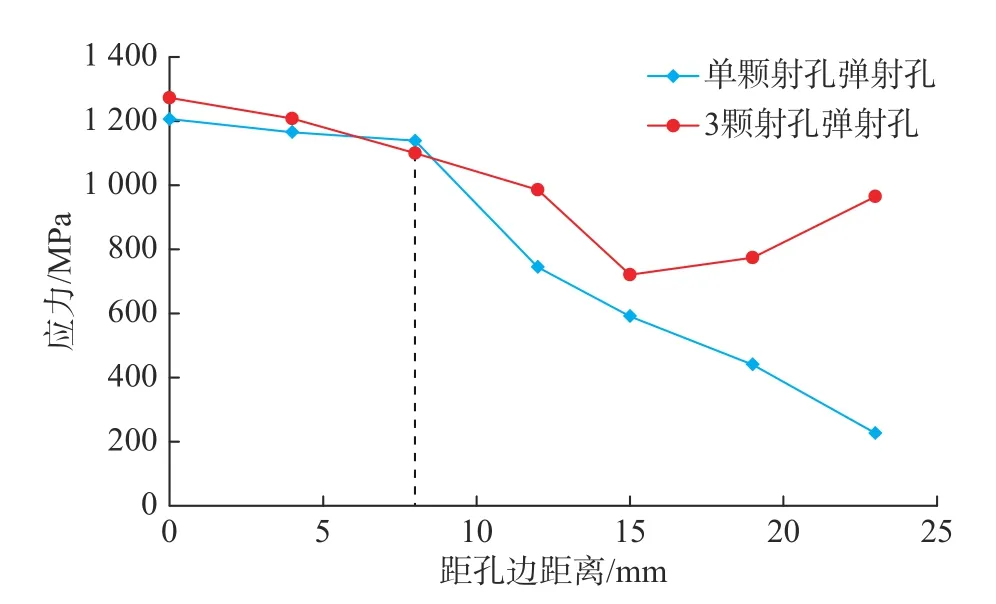
图13 单枚和3 枚射孔弹射孔时套管应力变化曲线Fig.13 Variation of the casing stress during the perforation of one perforating charge and three perforating charges
6 结论与建议
(1)应用LS-DYNA 软件,建立了射孔弹-射孔枪(含盲孔)-套管的三维有限元模型,采用ALE 算子分离算法,实现了爆轰过程、射流高速侵彻套管、药型罩固流转化的大变形和流固耦合仿真,分析了射孔枪和套管的强度安全性。
(2)射孔枪内外壁孔眼直径分别为24.4 mm 和13 mm,平均孔径为18.7 mm。套管内外壁孔眼直径分别为7.6 mm 和7.8 mm,平均孔径为7.7 mm,相差11 mm,说明穿透射孔枪盲孔过程消耗了大量能量,应合理设计盲孔壁厚。
(3)射孔枪的高应力区叠加、重合,使得此区域内材料应力增大,在射孔枪各孔相连的长250 mm、宽125 mm 的宽带内,其最小应力也达到了774 MPa,这一条宽带应力值均超过其屈服强度,在高爆轰压力的作用下,会产生向外的鼓胀。
(4)爆轰波叠加作用区域和孔边以20 mm 为半径的圆环应力变化区为射孔爆轰引起的套管应力加强区,相当于材料产生了“冷作硬化”,射孔结束后该区域范围内的材料不再符合原材料的应力应变曲线规则,材料力学属性会发生变化,强度会略有提高,但韧性降低,材料变脆,影响套管的强度安全。
