基于鱼群优化BP神经网络的切削温度建模*

王 晔，马廉洁,2，左宇辰，刘 涛，白 威，常 昊

(1.东北大学 机械工程与自动化学院，沈阳 110819；2.东北大学秦皇岛分校 控制工程学院，河北 秦皇岛 066004)

0 引言

陶瓷因为导热性差，切削加工过程中产生的热量容易局部积累，造成较大的热量梯度和热应力，进而引起刀具崩刃或者工件崩碎，降低刀具使用寿命，影响工件加工精度和表面加工质量[1-4]。研究和利用陶瓷切削热变化规律可以尽量避免加工事故，提高加工质量，节约加工成本[5-6]。但由于陶瓷材料具有电绝缘、热导率低、脆性大等特点，切削温度测量难度很大，因而针对陶瓷等脆性材料切削温度的研究较少[7]。Ma等[7]在断裂力学的基础上建立了切削温度模型，但对陶瓷材料切削温度模型的研究主要集中在理论模型上，而对切削温度算法模型方面的研究几乎未涉及。

BP神经网络是迄今为止应用最广泛的神经网络。但BP神经网络具有收敛速度慢和易陷入局部极值等缺点，而鱼群算法全局寻优能力强，能够快速找到全局最优值[8-11]。本文以鱼群算法优化后的BP神经网络，建立三个切削温度的一元预测模型。根据一元模型提出多元模型，并使用遗传算法进行多元模型的求解，从而获得陶瓷材料切削温度的算法多元模型，并进行了试验验证。

1 切削氟金云母试验

在CAK5085D型车床上，选用YG硬质合金刀具车削氟金云母，工件直径为30mm，采用数字式辐射温度传感器在线采集温度，分别进行了单因素试验和正交试验，试验条件如表1和表2所示。

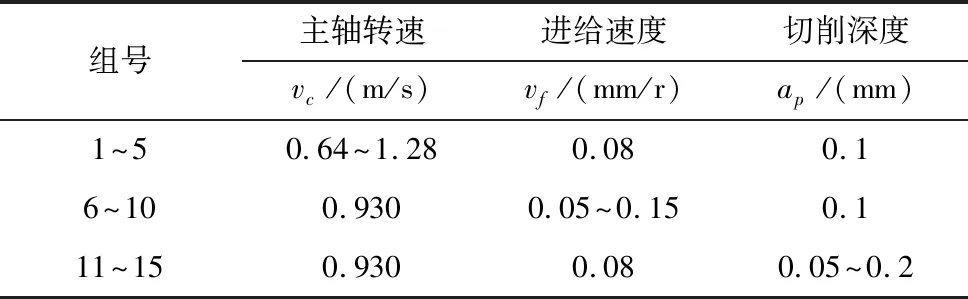
表1 单因素试验表

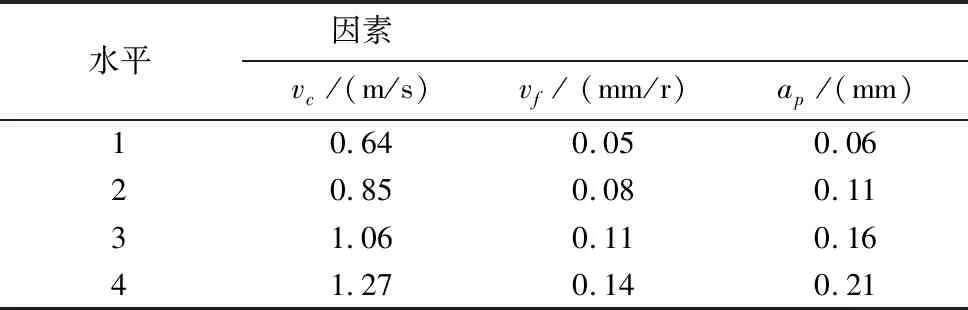
表2 正交试验因素水平表

2 鱼群优化BP神经网络

BP神经网络是前馈网络，学习过程包括信息的正向传播和误差的反向传播。BP神经网络的误差函数是非线性的，具有许多局部极小点，且BP网络是沿误差函数梯度下降方向来寻找最优点，如果初始权值阈值值选择不当，网络很容易陷入局部极小值[12-13]。

人工鱼算法是仿照鱼的运动规律，利用其个体模拟觅食、群聚和追尾行为，通过个体的局部寻优来实现全局寻优[14]。人工鱼通过探索周边环境和伙伴状态后，汇集在几个局部最优的位置处，其值越优，聚集的人工鱼数目越多，这有助于判断并获取全局最优值[15]。

人工鱼群优化BP神经网络的权值和阈值能很好的克服BP神经网络易陷入局部极值的缺点。设置输入神经元为3，隐含层神经元为5，输出层神经元为1的三层神经网络，隐含层传递函数为tansig函数，输出层传递函数为purelin函数。每条人工鱼由15个数据组成，代表即将优化的15个权值和阈值，开始进入鱼群寻优过程，评价函数为经BP神经网络训练过的输出数据与试验结果的均方根误差，流程图见图1。鱼群最终寻得的最优解就是BP神经网络15个最优的权值阈值。

图1 人工鱼群优化BP神经网络

3 单因素建模及机理分析

3.1 切削速度-切削温度建模

图2所示为切削温度随着切削速度vc变化曲线，陶瓷切削过程中，主要有两个热量来源，一个是后刀面和工件摩擦生热，另一个是化学键形成和断裂的能量差转化的热能，称之为化学热。陶瓷因为导热性较差，切削过程产生的化学热大部分依附在切屑表面，随着切屑脱离。

切削开始时，切削速度较小，摩擦热较小，化学热占主要部分主导切削热的变化，随着切削速度增加，切屑表面依附的热量未来得及向刀具传导，快速流失，所以切削温度随着切削速度增加而下降。随着切削速度的增加，转动频率渐渐接近材料固有频率，工件振动加剧，开始出现崩碎，且工件已加工表面粗糙度增加，后刀面和工件间摩擦力骤增，温度开始随着切削速度增加，而后主轴转动频率渐渐远离材料固有频率，工件振动减小，切削温度下降。随着切削速度增大，摩擦热逐渐占主要地位，随着切削速度增加，摩擦热增加，切削温度上升。

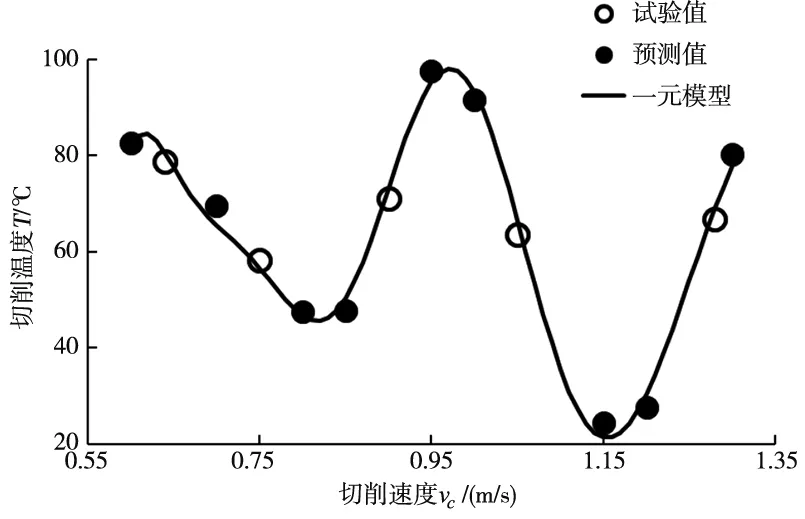
图2 切削速度对切削温度的影响

根据图2中数据点的变化趋势，提出一元模型：

T=a(bvc2+cvc+d)egvc+hsin(kvc2+lvc+m)+n

根据最小二乘拟合法求得模型：

T=17.9869(340.8082vc2-477.3235vc+168.7438)·
e-4.7591vc+2.0373sin(-6.7148vc2+30.6455vc-15.4653)+
62.0333

模型相关系数R=0.9934。

3.2 进给速度-切削温度建模

图3所示随着进给速度增加，陶瓷对刀具的反作用增大，后刀面磨损加快，后刀面和已加工表面接触体积减少，摩擦力下降，切削温度下降；随着进给速度增大，单位时间内去除材料增加，产生的化学热增加，使温度略有回升但是摩擦热仍占很大比例，随进给速度增加，刀具磨损加剧，切削温度再次下降；随着进给速度增大，刀具磨损趋于稳定，化学热增加，切削温度上升。

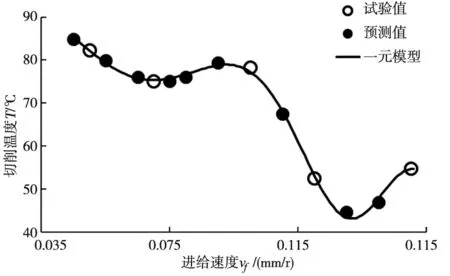
图3 进给速度对切削温度的影响

根据图3中数据点的变化趋势，提出一元模型：

T=a(bvf2+cvf+d)sin(gvf2+hvf+k)+l

根据最小二乘拟合法求得模型：

T=-2.2470(-1006.8074vf2+60.0508vf+14.6172)·
sin(853.6908vf2-113.9551vf+1.4154)+53.7730

模型相关系数R=0.9988。

3.3 切削深度-切削温度建模

图4所示切深较小时，车刀刃磨与工件接触面积小，后刀面与工件接触面积小，化学热占主要地位，切深增大，释放的化学能增多，切削温度升高；随着切深增加，切屑轻崩碎，切屑产生表面释放的热量减少，刀具和工件摩擦减少，切削温度轻微下降；随切削深度增加，工件和刀具均有崩碎现象，产生不平整的工件和刀具表面，摩擦力急增，切削温度快速上升。

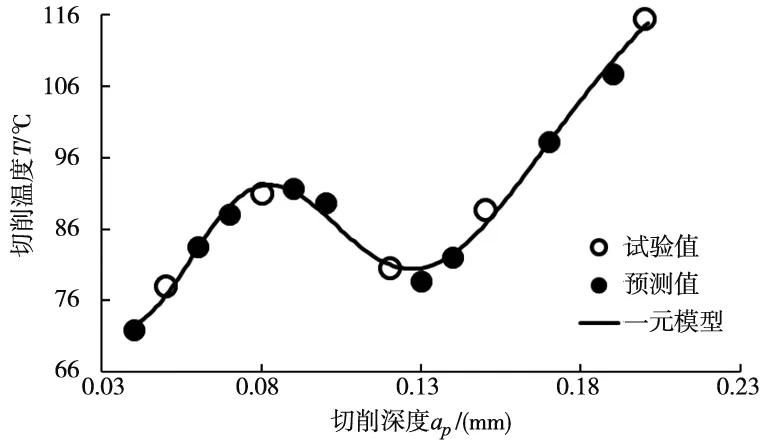
图4 切削深度对切削温度的影响

根据图4中数据点的变化趋势，提出一元模型：

T=a(bap2+cap+d)sin(gap2+hap+k)+l

根据最小二乘拟合法求得模型：

T=4.2090(-673.2706ap2+92.3455ap-0.3340)
sin(163.7046ap2-77.9516ap+0.7466)+80.9318

模型相关系数R=0.9944。

4 多元建模及验证

根据提出的切削速度-切削温度、进给速度-切削温度、切削深度-切削温度3个一元模型，提出多元模型形式：

T=

a(bvc2vf2ap2+cvcvfap+d)egvc+hsin(kvc2vf2ap2+lvcvfap+m)+n

根据遗传算法，结合表2前13组正交实验数据求解出多元模型：

取表2前13组正交试验温度值与多元模型值进行对比，如图5所示。将正交试验后3组对应的切削参数代入模型计算。所得模型值和试验值对比，验证模型精度。误差分别为0.9907%，3.5765%，9.3284%。

图5 试验值与模型计算值对比

5 结论

采用鱼群优化BP神经网络结合最小二乘拟合法得到了切削温度的一元预测模型，采用遗传算法得出了切削温度的多元模型，验证实验表明了模型具有较高的准确性。因通过观察切削温度随三个切削工艺参数变化趋势进而提出切削温度多元模型的难度较高，所以提出通过观察切削温度分别随3个切削工艺参数的变化趋势建立3个一元模型进而提出一个切削温度多元模型的可靠性较高。切削温度多元模型的提出可为切削加工过程中切削温度的变化提供预测，对工件加工精度以及刀具寿命提供了理论基础，同时对切削参数的合理选择提供了依据。