基于VMD和PCT的旋转机械故障诊断方法研究*

徐 飞，蒋占四，余 鼐, 黄惠中，杨庆勇

(桂林电子科技大学 机电工程学院,广西 桂林 541004)

0 引言

作为机械装备的重要组成部分，旋转机械的可靠性有利于保障设备运营的稳定和安全。旋转机械的失效主要由构成其旋转部件导致的，主要为齿轮和轴承的故障及失效[1]。基于振动信号分析和处理的方法是故障诊断的常见方法。齿轮故障的振动信号大多呈现以啮合频率为主要中心频率[2]，以故障齿轮所在轴转频为主要调制频率的边频带的特征。同样，轴承出现故障时，多呈现以轴承部件的共振频率为载波频率，以故障频率为调制频率的特征[3]。因此，可以通过对调制频率的分析得到故障信息。

时频分析方法通过对信号特征的拟合而适用于调频信号的分析和处理。YU等[4]采用自适应高斯调频小波提取振动信号的时频特征信息，使用独立成分分析方法精简特征并结合自组织神经网络来实现滚动轴承故障的诊断。皮维等[5]使用线调频广义解调方法和频谱分析方法并将其应用到齿轮的故障诊断中。以上方法表明调频小波方法对于提取轴承、齿轮调制特征的有效性。作为一种参数化时频方法，多项式调频小波变换(PCT)具有优良的时频聚集性，其不仅能够用于线性调频信号的处理，同样也能适用于非线性调频信号[6]。但和其他参数化时频分析方法一样不适用于分析多频率组分信号[7]。变分模态分解(VMD)能够将原始信号分解成若干离散的子频带，并且在信号模态分离方面克服了经验模态分解存在模态混叠和端点效应的缺点[8]。ZHANG等[9]使用VMD方法将轴承信号分解并检测主模态特征，通过分析包络谱实现轴承故障的诊断。程军圣等[10]将主模态分析用于带宽限制的本征模态函数排序，使用萤火虫算法优化VMD参数，实现了齿轮的故障诊断。

本文融合VMD对多分量信号分解和PCT对调频信号特征提取的各自的优势，将VMD算法作为PCT算法的前处理算法，选取VMD分解后周期性特征最明显的模态分量作为PCT算法的输入得到时频图，对时频图进行分析从而实现齿轮和轴承的故障诊断。并通过实验验证了该方法能够对旋转机械中的齿轮和轴承进行有效的故障诊断。

1 算法原理介绍

1.1 VMD算法原理

变分模态分解能够将信号分解成若干离散的子频带，即模态uk。模态具有稀疏性且紧紧围绕中心频率ωk脉动。解调信号的脉动带宽可以通过H1高斯平滑来估计，算法如下：

(1)

通过引入拉格朗日乘子λ重建约束，将式(1)转变为无约束问题。引入拉格朗日乘子的问题构造如下：

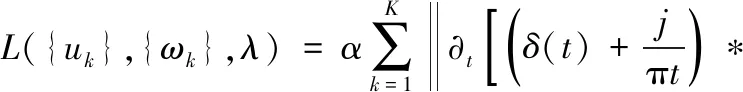
(2)

式(2)可以通过交替乘子方向法(ADMM)来求解。

估计模态uk(t)和中心频率ωk的更新算法如下：

(3)

(4)

VMD算法可以分为4个主要步骤：

(2)根据公式(3)和公式(4)更新uk和ωk；

(3)对于所有的ω≥0,拉格朗日乘子λn+1通过以下公式更新。

(5)

(4)对于一个给定的迭代精度ε,迭代过程按照以下公式终止。

(6)

1.2 PCT算法原理

传统调频小波变换(CT)在信号的瞬时频率轨迹为时间的线性函数情况下，通过选择合适的调频比率就能够获得优良聚集性的时频分布。但一旦瞬时频率变为动态非线性时，CT的线性近似就不再适合表示瞬时频率轨迹。多项式调频小波变换(PCT)是为了克服CT的不足而被提出，具体公式如下：

(7)

其中，

(8)

(9)

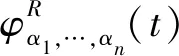
PCT算法的原理如图1所示，该算法主要分为3个步骤：

(3)以ω(σ)为窗函数，对平移后的信号进行短时傅里叶变换(STFT)。

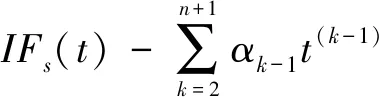
图1 PCT算法原理图

2 实验验证2.1 齿轮故障实验验证

2.1.1 齿轮实验装置

风力涡轮机动力传动故障诊断综合实验台(WTDS)，其动力转动系统主要由一个二级传动平行轴齿轮箱，行星齿轮箱及磁力制动器组成。

该平台的驱动电机为3马力，实验齿轮z1位于与电机相连的输入轴，压电传感器安装在平行轴齿轮箱上，通过VQ数据采集系统采集振动数据。

齿轮箱内部结构如图2中a所示，实验齿轮分为断齿故障和齿根裂纹故障，如图2中b和c所示。两种不同类型的故障齿轮试验时，输入轴转频均为29.81Hz，采样频率为25.6kHz。

实验齿轮z1的啮合频率(一级传动啮合频率)为864.49Hz，二级传动啮合频率为313.2Hz。

图2 齿轮箱内部结构图及故障齿轮

2.1.2 齿轮断齿故障分析

数据采集系统采集到的齿轮断齿故障振动信号如图3所示，受系统噪声干扰及信号调制作用，在时域图和频域图上不能判断出齿轮的状态。对振动信号进行PCT，结果如图4所示，同样不能判断出该齿轮的状态。

(a) 时域图

(b) 频域图 图3 齿轮断齿故障振动信号

图4 齿轮断齿故障PCT变换

对齿轮的振动信号进行VMD，通过VMD方法使振动信号的模态得到了分离，选择具有最明显周期性成分的模态对其进行PCT，结果如图5所示。

图5 齿轮断齿故障特征模态的PCT变换

通过时频图可以得到故障频带和循环周期，由循环周期求倒数可以计算出循环频率。由图5可知，故障频带在一级啮合频率附近波动，从而诊断出齿轮箱的第一级传动出现了故障，但第一级传动有两个齿轮，分别是齿数为29的小齿轮和齿数为100的大齿轮。此时还无法诊断出哪一个齿轮出现了故障。通过时频图上周期性的循环，得到循环周期为0.03406s，即循环频率为29.36Hz。这与输入轴转动频率29.81Hz很接近，综上可以判定输入轴上的小齿轮z1出现了故障。

2.1.3 齿轮齿根裂纹故障分析

数据采集系统采集到的齿轮齿根裂纹故障振动信号如图6所示，受系统噪声干扰及信号调制作用，在振动时域图和振动频域图上不能判断出齿轮的状态。对振动信号进行PCT，结果如图7所示，同样不能判断出该齿轮的状态。

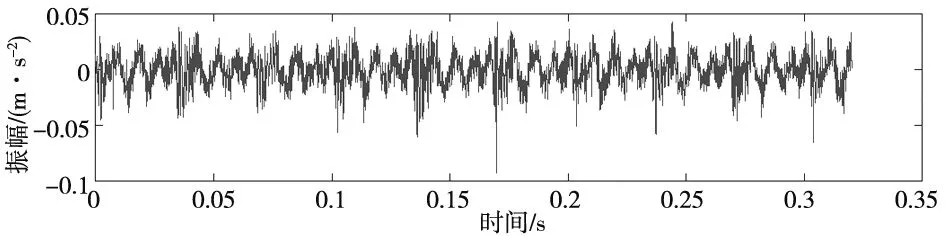
(a) 时域图

(b) 频域图 图6 齿轮齿根裂纹故障振动信号

图7 齿轮齿根裂纹故障PCT变换

对齿轮的振动信号进行VMD，通过VMD方法使振动信号的模态得到了分离，并选取具有最明显周期性成分的模态分量。对其进行PCT，结果如图8所示。

通过时频图可以得到故障频带和循环周期，再由循环周期求倒数可以得到循环频率。由图8可知，故障频带在一级啮合频率附近波动从而判断出齿轮箱的第一级传动出现了故障。由于第一级传动有两个齿轮，同样要通过时频图上周期性的循环，得到循环周期为0.0337s，即循环频率为29.67Hz。这与输入轴转动频率很接近，综上可以判定输入轴上的小齿轮z1出现了故障。

图8 齿轮齿根裂纹故障特征模态的PCT变换

2.2 轴承故障实验验证

2.2.1 轴承实验装置

轴承故障所使用的机械故障综合模拟实验平台(MFS-MG)，其主要由信号采集和调速软件系统，驱动电机，转速计，加速度传感器及故障轴承组成。

该平台的驱动电机为1马力，故障轴承的型号为ER-12K，滚动体直径为7.9375mm，节圆直径为33.4772mm，滚动体数目为8，接触角为0°。采样频率为12.8kHz，内圈故障轴承的转动频率为29.87Hz，外圈故障轴承的转动频率为29.84Hz。经过计算得到内圈故障轴承的特征频率为147.8Hz、外圈故障轴承的特征频率为91.1Hz。

2.2.2 轴承内圈故障分析

数据采集系统采集到的轴承内圈故障振动信号如图9所示。对振动信号进行PCT，结果如图10所示，由图10不能推断出轴承是否出现了故障。

(a) 时域图

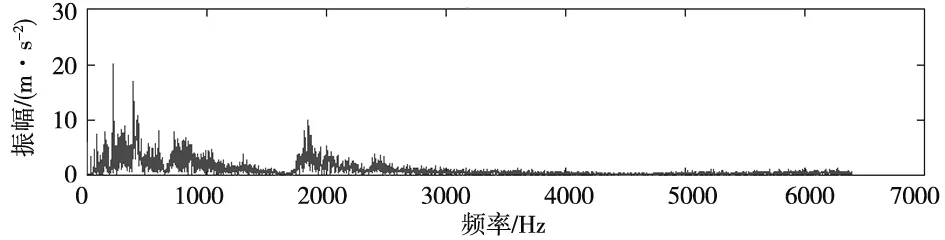
(b) 频域图 图9 轴承内圈故障振动信号

图10 轴承内圈故障PCT变换

对轴承的振动信号进行VMD，通过VMD方法使振动信号的模态得到了分离，选择周期性特征最明显的模态进行PCT，结果如图11所示。通过时频图可以得到循环周期，对循环周期求倒数得到循环频率。由图11得到循环频率为149.3Hz。其与内圈故障轴承的特征频率147.8Hz很接近，可以判定轴承内圈出现了故障。

图11 轴承内圈故障特征模态的PCT变换

2.2.3 轴承外圈故障分析

数据采集系统采集到的轴承外圈故障振动信号如图12所示。对振动信号进行PCT，结果如图13所示，由图13不能推断出轴承是否出现了故障。

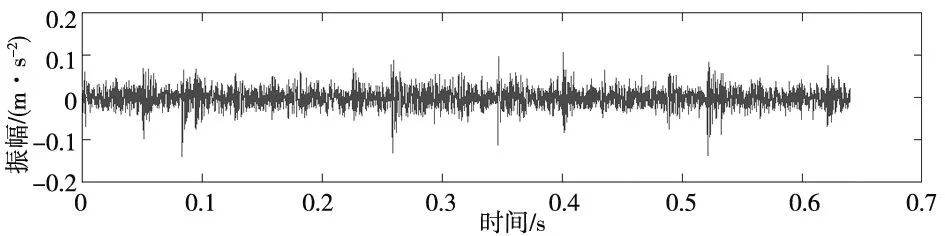
(a) 时域图

(b) 频域图 图12 轴承外圈故障振动信号

图13 轴承外圈故障PCT变换

同样，对轴承的振动信号进行VMD，通过VMD方法使振动信号的模态得到了分离。选择周期性特征最明显的成分对其进行PCT，结果如图14所示。通过时频图可以得到循环周期，对循环周期求倒数得到循环频率。由图14得到循环频率为90.9Hz。其与外圈故障轴承的特征频率91.1Hz很接近，可以判定轴承外圈出现了故障。

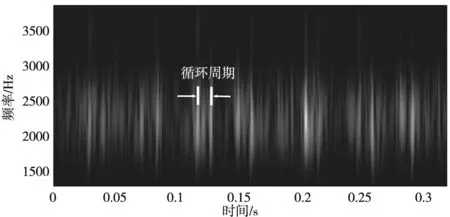
图14 轴承外圈故障特征模态的PCT变换

3 结束语

本文所提出的基于VMD和PCT的旋转机械故障诊断方法，将VMD在多分量信号分解和PCT对于调频信号特征提取的优势相融合，得到聚集性高的时频图。通过分析齿轮时频图上的故障频带和循环周期从而诊断出齿轮故障，分析轴承时频图上的循环周期从而诊断出轴承故障。所提出的方法比单一的PCT方法效果明显具有优势。最后通过齿轮及轴承实验平台验证了该方法的有效性。