基于CEEMD和小波核极限学习机的轴承故障诊断

邹剑晖，敖银辉

(广东工业大学 机电工程学院，广州 510006)

0 引言

在轴承的故障诊断领域中，基于振动信号分析的方法是目前最有效的方法。其中，利用适用的信号处理方法从振动信号中有效提取故障特征是实现轴承故障诊断的关键[1]。Huang等[2]提出了自适应信号处理方法，即经验模态分解(EMD)和集合经验模态分解(EEMD)，但这两种方法都会受到模态混叠效应的影响。Yeh等[3]提出了补充集合经验模态分解(Complementary Ensemble Empirical Mode Decomposition，CEEMD)，该方法完全解决了模态混叠的问题。熵可以反映信号的复杂程度，通常被用作故障信息的特征参数。Pincus提出了近似熵，Richman等人提出了样本熵[4]，但是这样的单尺度熵算法在数据处理时经常会得到相互矛盾的结果，后来Costa等[5]提出了多尺度熵(Multiscale Entropy，MSE)的概念。极限学习机(Extreme Learning Machine，ELM)是一类针对单层前馈神经网络(Single Layer Feedforward neuron Network，SLFN)设计的机器学习算法[6]，具有学习能力快，泛化能力强等优点[7]。

大量机械零件故障诊断研究领域的文献使用EEMD和支持向量机或者神经网络的结合模型。文献[8]结合EEMD和ELM进行齿轮诊断；文献[9]提出一种基于EEMD和SVM的识别滚动轴承退化状态的方法；文献[10]利用多尺度熵提取特征。由于SVM在大规模训练样本中的局限性和传统BP神经网络易陷入局部极小化等问题，本文提出一种CEEMD多尺度熵和小波核极限学习机(Wavelet Kernel ELM，WKELM)结合的故障诊断方法。

本文将以滚动轴承作为研究对象，针对几种典型的工作模式如滚动轴承正常工况、外圈故障、内圈故障和滚动体故障，分析相关振动信号数据，利用CEEMD多尺度熵提取特征，采用WKELM模型来对滚动轴承进行故障诊断，相对于传统的神经网络等方法提高了诊断准确率。

1 基于CEEMD多尺度熵的特征向量提取

EMD算法从原信号中提取出若干个固有模态分量IMF，但会产生模态混叠。EEMD将白噪声加入到原始信号当中，有效抑制了模态混叠，但添加的白噪声会使得IMF分量重构时产生误差。

为了解决上述白噪声干扰且无法完全被中和的问题，CEEMD算法通过给原始信号添加符号相反的白噪声，分别对两组信号进行EMD分解，重构误差得到了明显减少，添加的白噪声得到了最大限度地中和。

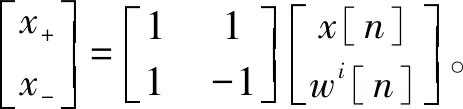
(3)通过多组分量组合的方式得到分解结果，即CEEMD分解最终得到的IMF分量：

(1)

多尺度熵的实质就是在不同尺度因子下计算给定数据的样本熵，设原始数据长度为X={x1,x2,…,xN}，预先给定相似容量r和嵌入维数m，计算过程如下：

(1)对原始数据X进行粗粒化处理，建立新的粗粒化向量yj(τ)。

(2)求N个粗粒向量的样本熵，由在尺度τ下的粗粒化序列组成m维数矢量Y(i)。

(4)当重构m维数据时，求样本的平均值相似度Bm。

(5)重复步骤(2)～步骤(4)得到Bm+1(r)，则原始信号序列的样本熵为：

(2)

(6)计算每一个尺度因子序列的样本熵，则可得到MSE，即MSE(x,τ,m,r)=SampEn(yτ,m,r) 。

结合CEEMD和多尺度熵进行滚动轴承故障特征提取，首先用CEEMD将滚动轴承振动信号分解为多个IMF分量，然后根据相关系数法筛选出5个包含有效信息最多的分量，再计算5个IMF分量的多尺度熵值，构造出五维故障特征向量。多尺度熵值的计算与尺度因子τ、相似容量r和嵌入维数m有关，依据本文数据和以往经验，尺度因子τ取10，相似容量r取原始信号数据标准差的0.2倍，嵌入维数m取2。

2 小波核极限学习机建模

极限学习机是一种单隐层前馈神经网络SLFN学习算法，相对于传统神经网络具有学习速度快，泛化性能好的优点。该算法只用设置网络的隐含层节点个数和核函数，不需要设置输入层与隐含层间的连接权值和隐含层神经元的阈值，便可以得到唯一的最优解。

极限学习机的数学模型可以表述为：给定任意Q个不同样本(xi,ti)，其中xi∈Rn为输入样本，ti∈Rm为输出样本，设隐含层神经元个数为L，核函数为g(x)，则输出可表示为：

(3)

上式可简化成：

Hβ=T′

(4)

其中，wi为输入层与隐含层的连接权值，bi为隐含层神经元的偏置，βi为输出权值。

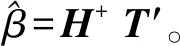
综上，ELM的学习算法如下：

(1)确定隐含层神经元的数量，随机设置输入层神经元和隐含层神经元间的连接权值w和隐含层神经元的偏置b；

(2)选取适当的函数作为隐含层神经元的核函数，并计算出隐含层的输出矩阵H；

为进一步提高ELM的分类能力，将小波核函数引入ELM。一般的ELM使用的核函数为′sig′(默认)、′sin′和′hardlim′，而基于Morlet小波在数据处理方面的优越性，小波核函数可以实现逼近任意函数，泛化能力更强且在非线性分类平面上的效果更佳。

核极限学习机的核函数需要满足平移不变性定理和Mercer条件，因此本文选用Morlet小波函数h(x)=cos 1.75x·exp (-x2/2)，其相应的小波核函数表达式为：

(5)

式中：a为尺度因子。

3 轴承故障模式分析和诊断

轴承是重要的旋转运动部件，其状态直接关系着设备的稳定运行。轴承失效模式多种多样，简单分类有内圈故障、外圈故障和滚动体故障，任何一种故障都会影响轴承正常运转，进而导致机械设备产生故障，因此制定一种高效的故障诊断方法具有实际意义，基于振动信号的测试分析是轴承故障诊断的主要方法。

本文使用的轴承振动实验数据来自美国凯斯西储大学电气工程实验室的滚动轴承故障模拟实验台所测得的数据，实验时电机转速1797 r/min，采样频率为12kHz，数据采自驱动端电机上型号为6205 2RS JEM SKF的深沟球轴承，其结构参数如表1 所示。

表1 轴承结构参数

本文首先利用CEEMD分解原始信号，根据包络谱分析得到故障特征频率，验证CEEMD的优越性能。然后，利用多尺度熵进行特征向量提取，输入到小波核极限学习机中训练和测试。该数据处理过程如图1所示。

图1 数据处理过程

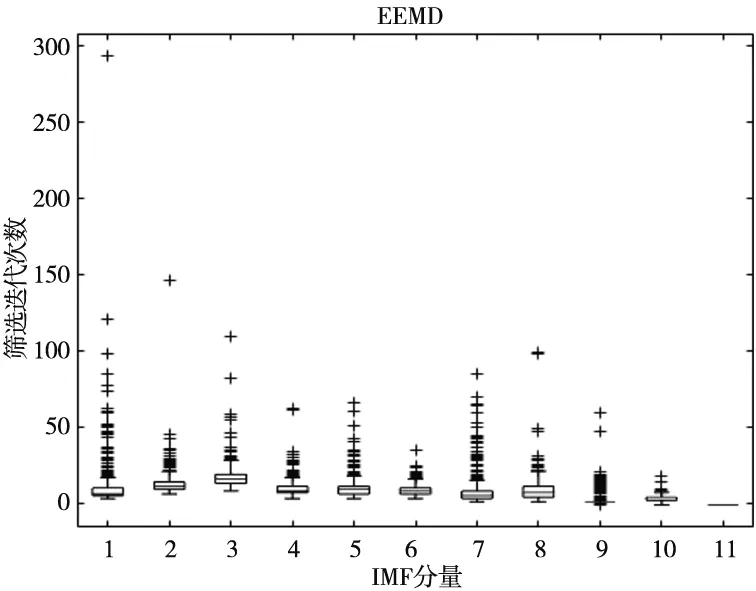
以驱动端轴承外圈故障数据为例，截取一段信号进行CEEMD分解，信号分解产生的IMF分量如图2所示，再对这一段截取信号进行EEMD分解，对比两次分解过程的箱型图，如图3所示。

(a) 原始信号、IMF1和IMF2

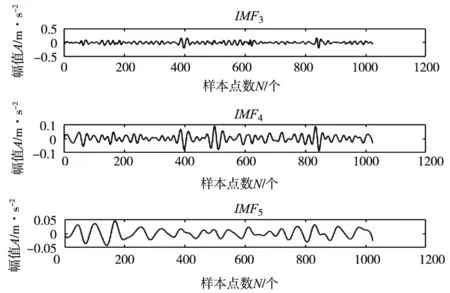
(b) IMF3、IMF4和IMF5

(c) IMF6、IMF7和IMF8

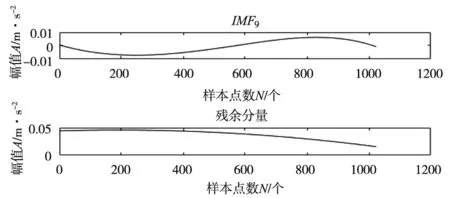
(d) IMF9和残余分量 图2 轴承外圈故障振动信号及其CEEMD分解结果

(a) EEMD筛选迭代次数

(b) CEEMD筛选迭代次数 图3 EEMD和CEEMD的筛选迭代次数对比

由图2可知，CEEMD分解后的IMF按频率高低排列，振幅依次减弱，各IMF平稳且没有模态混叠现象。由图3可知，CEEMD算法迭代的次数仅为EEMD的58.6%，降低了计算成本。

CEEMD分解后利用相关系数法筛选出与原始信号相关性大、包含最多有效信息的IMF分量，重构后做傅里叶变换得到的包络谱如图4所示。

图4 重构信号的包络谱

由图4可知，该发生外圈故障的滚动轴承的特征故障振动频率为105.5Hz，与理论特征故障振动频率一致。同时，在图4中还可以找到它的二倍频210.9Hz和三倍频316.4Hz，并且频率突出，没有受到噪声干扰埋没，因此该CEEMD算法在本次处理的轴承信号数据中是有效的。

根据第1节理论，输入到小波核极限学习机的特征向量可以由多尺度熵来构造。因此，首先要选取出可用的特征向量，通过计算各分量与原始信号的相关系数即可筛选出有效IMF分量。

对于该次实验，本文为4种工况分别构造了115组样本，每组样本数据的长度是1024，组合成460×1024的矩阵样本进行处理。

本文拟在每组数据中筛选出5个最能反映原始信号特点的特征向量，选取第一组样本数据进行处理，计算4种工况数据的IMF相关系数，如表2所示，列出了前7个IMF的计算结果。

表2 各工况数据的前7个IMF分量的相关系数

由表2可知，正常工况和故障工况数据经过CEEMD分解后，得到的IMF分量与原始信号的相关性由高到低排列，其中前5个IMF与原始信号相关系数较大，可以用来构造特征向量。计算前5个IMF分量的多尺度熵值，如表3所示。

表3 各工况数据的前5个IMF分量的多尺度熵值

根据表3中4种工况数据分解后的IMF分量多尺度熵值，结合经验可知，各工况下的多尺度熵值基本反映了对应工况的振动特点。

为验证表3的结果不存在偶然性，每种工况选取32组样本，各取前3个IMF分量的多尺度熵值，构造CEEMD-多尺度熵特征向量，可视化特征提取结果如图5所示，图中不同工况构造的特征向量之间界限清晰，类内聚集性良好，其中正常工况的特征向量与3种故障工况的特征向量分离明显，因此本方法构造的4种特征向量能够真实反映其对应工况的信号特点。

图5 CEEMD-多尺度熵故障特征向量

将得到的特征向量作为输入特征输入小波核极限学习机进行分类，从而达到识别输入特征所属信号归于哪类工况的目标。

本文采用交叉实验的方法，对构造的样本进行了6次分类识别。其中，样本总数为340，包括250个训练集样本，90个测试集样本，根据多次实验总结，设置隐含层神经元个数为100。首先，将正常工况样本与3种故障工况样本进行分类识别，每次实验中，训练集样本由170个正常工况样本和80个故障工况样本组成，测试集由60个正常工况样本和30个故障工况样本组成，其结果如表4所示。

然后，对3种故障工况样本之间进行相互识别，共3组实验，结果如表5所示。此次识别中的前两组实验用外圈故障样本取代了表4实验中正常工况样本，样本数目保持不变，命名为主样本，训练集和测试集中的少数部分样本则由内圈故障样本和滚动体样本取代，命名为副样本。表中第3组实验的主样本和副样本则分别是内圈故障样本和滚动体样本。

表4 正常工况和故障工况的分类结果

表5 3种故障工况的相互分类结果

根据表4和表5可知，小波核极限学习机在分类准确率上表现优异，本文还利用支持向量机和BP神经网络进行识别，最终效果与本文所用方法对比如表6所示。

表6 小波核极限学习机与其他分类方法的结果比较

4 结论

本文利用CEEMD多尺度熵和小波核极限学习机结合的诊断方法，对滚动轴承进行故障诊断，具有良好效果。其中，CEEMD算法解决了模态混叠问题，多尺度熵提取出的特征很好地反映出原始信号的特点，结合小波核极限学习机实现了精确诊断。与SVM和BP神经网络相比，本文所提出的方法的诊断精度最高，达到97.96%，可以运用在实际滚动轴承故障信号诊断上。