张量Z-特征值的新包含域定理

何 军, 唐 兰, 刘衍民

(遵义师范学院 数学学院, 贵州 遵义 563006)

1 引言与预备知识

张量特征值是矩阵特征值的推广,并广泛应用到医学成像、图像分割和量子计算等问题中[1-7].令A=(ai1i2…im),ai1i2…im∈R,Qi[1]给出了如下的张量Z-特征值的定义.

定义 1[1]设A∈R[m,n](m阶n维),若存在非零向量x∈Rn和数λ∈R使得

Axm-1=λx,xTx=1,

其中

则称λ为张量A的Z-特征值,x为属于λ的Z-特征向量.

令

N={1,2,…,n},为了对张量Z-特征值的性质做进一步的研究,Wang等[8]给出了如下的张量Z-特征值包含域定理.

引理 1[8]设A∈R[m,n],则

(1)

其中σ(A)表示张量A的谱,

Nij(A)={z∈C:(|z|-

(Ri(A)-Pii(A)))|z|≤Pii(A)Rj(A)},

若关于张量A的多项式满足Axm=mAxm-1,则称张量A为弱对称的.令张量A的Z-谱半径

ρ(A)=sup{|λ|:λ∈σ(A)},

Chang等[9]给出了如下的非负张量Z-特征值Perron-Frobenius定理.

引理 2[9]设A∈R[m,n]是非负不可约且弱对称的张量,则ρ(A)是张量A的正Z-特征值,并且ρ(A)对应的Z-特征向量是正向量.

基于引理1和引理2,Wang等[8]给出了如下的非负张量Z-谱半径上界.

引理 3[8]设A∈R[m,n]是非负弱对称不可约的张量,则

本文考虑阶数大于3的张量,给出了张量Z-特征值的新包含域定理,并通过张量Z-特征值的新包含域定理,给出了非负张量Z-谱半径的新上界.数值例子说明本文结果优于文献[8]中的结果.

2 主要结果

对任意p,k∈N,令

Δk={(i2,…,im):i2,…,im中至少有2个等于k},

Δpk={(i2,…,im):i2,…,im

中至少有1个等于p,2个等于k},

中至少有1个等于p,最多有1个等于k},

中没有1个等于p,至少2个等于k},

中没有1个等于p,最多有1个等于k}.

定理 1设A∈R[m,n],m≥4,则

(2)

其中

Kij(A)={z∈C:(|z|-αΔiki(A)-

证明设非零向量x∈Rn是张量A的Z-特征值λ对应的Z-特征向量,即

Axm-1=λx.

(3)

令|xp|≥|xs|≥max{|xk|:k∈N,k≠s,k≠t},由(3)式可得

(4)

在(4)式两边同时取绝对值有

当m≥4时有

(5)

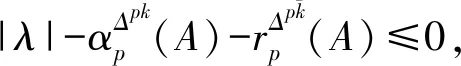
如果|xs|>0,由(3)式可得

(6)

由(5)和(6)式可得

证毕.

注 1由定理1的证明可得

|z|-(Ri(A)-Pii(A))≤

则若

成立,则有

(|z|-(Ri(A)-Pii(A)))|z|≤Pii(A)Rj(A),

即L(A)⊆K(A).基于定理1可得如下非负弱对称不可约张量的Z-谱半径的新上界.

定理 2设A∈R[m,n]是非负弱对称不可约的张量,则

证明由引理2,设正向量x∈Rn是非负弱对称不可约张量A的Z-谱ρ(A)对应的Z-特征向量,即

Axm-1=ρ(A)x.

由定理1可知,存在p,s∈N使得

即

证毕.

注 2由注1的可得L(A)⊆K(A),即定理2所得非负弱对称不可约张量的Z-谱半径的新上界始终比引理3(文献[8]的定理3.4)的上界好.

3 数值例子

本节用数值例子来说明结果的有效性.

例 1设A=(aijkl)∈R[4,3]且

a1111=1,a1122=1,a1133=1,

a2211=2,a2222=3,a2233=2,

a3311=-2,a3322=-2,a3333=-3,

且其余的aijkl=0,则张量对A的Z-谱σ(A)={-3,1,3}.

图1为结果比较.由引理1可得

L(A)={z∈C:|z|≤7},

由定理1可得

K(A)={z∈C:|z|≤3}.

图1 L(A)与K(A)比较

由图1可以看出,定理1的结果比文献[8]中定理3.4的结果好.

例 2设A=(aijkl)∈R[4,2]且

a1111=1,a2222=2

且其余的aijkl=1,则张量对A的Z-谱σ(A)={0.077 8,4.285 6}.

由引理3(文献[8]中定理4.7)可得ρ(A)≤8.515 6.由定理2可得ρ(A)≤5.524 9.由例2可以看出,定理2的结果比文献[8]中定理4.7的结果好.

致谢遵义师范学院博士基金(遵师BS[2015]09)对本文给予了资助，谨致谢意.