短脉冲方程的周期波的波长

孙 旻, 张克磊

(桂林电子科技大学 数学与计算科学学院, 广西 桂林 541004)

非线性波动方程及其行波解的研究在物理学的许多领域中有非常重要的作用.本文研究短脉冲方程行波解的波长,其一般形式如下

(1)

将方程(1)写成如下形式

(2)

本文研究下列形式的行波解

u(x,t)=φ(x+ct),

(3)

其中c为波的传播速度.将方程(3)代入方程(2),可以得到对应的方程

cφ″-βφ2φ″-2βφ(φ′)2-αφ=0.

(4)

关于平面多项式微分系统的周期函数的研究已有诸多成果[5-12].然而,关于非线性波动方程的周期波的周期函数的研究成果甚少[13-15].众所周知,非线性微分方程的周期解的研究在许多物理领域有着非常重要的作用.Chen等[13]研究了φ6模型的周期波解的周期函数的临界周期,Geyer等[14]研究了Camassa-Holm方程的周期行波解的波长,郭丽娜等[15]研究了Vakhnenko方程的光滑周期波的波长;而本文主要研究方程(1)在α<0,β>0或β<0时,短脉冲方程的周期函数单调性.

1 短脉冲方程的行波解

方程(4)的对应行波系统，由下式给出

(5)

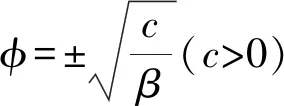
(6)

图 1 当α<0,β>0时,系统(5)的相图

图 2 当α<0,β<0时,系统(5)的相图

系统(6)的首次积分为

令

B(φ)=(c-βφ2)2,

因此,将首次积分(7)可写成以下形式

H(φ,y)=A(φ)+B(φ)y2.

(8)

令H(φ,y)=h，这里的h是一个积分常数,

h0=H(0,0)=0，

根据动力系统的理论,二阶微分方程(4)的每一个光滑周期解φ相当于系统的一个周期轨道.而每一个周期轨道γh都被包含在能量层{(φ,y):H(φ,y)=h}中并且周期轨道为

(9)

函数T(h)就是本文中的周期函数.所以如果计算出周期T关于h的导数,便可以得到周期函数的单调性和临界点的个数.

2 光滑周期波的波长

下面研究短脉冲方程(1)的光滑周期行波解的周期T对能量水平h的依赖性.由文献[14-15]知,在流体力学中,周期波解的周期对应的周期波的波长,即相邻2个波峰之间的距离,一般记为λ.另一方面,波峰与波谷之间的距离称为波高,记为a,见图3.下面给出理论与数值分析周期函数T(h)与波长函数λ(a)的性质.

图 3 波长为λ和波高为a的光滑周期波

命题 2.1若c>0并且β>0,则周期函数

(10)

是严格单调递减的，并且满足

(11)

证明因为

是沿着轨道γh的常数,因此

(12)

为了得到周期T关于h的导数,可以首先对(12)式的第二个积分做一个变换.由于周期轨道γh属于能量层{(φ,y):H(φ,y)=h},因此

(13)

(14)

令

(15)

(16)

此时，被积函数在拐点处不再是奇异的,轨线γh与水平轴相交.因此对(12)式关于h进行求导可以得到

其中

(18)

通过(17)式,得到

(19)

将

B(φ)=(c-βφ2)2

代入(19)式,做进一步计算便可得到

(20)

由于向量场关于水平轴对称,再根据首次积分,可以得到

(21)

而当β<0时,φ∈(-∞,+∞),其单调性的证明过程与上述内容一致,由于c-βφ2>0,依然可以得到(21)式,此时T′(h)>0.

(22)

并且

(23)

证明利用(7)式,可以把(9)式化为如下形式

(24)

其中拐点φ±是A(φ±)=h的根.为了证明(22)式,使用伸缩变换

把它代入到(24)式中立即得到一个新的积分

注意到,当h→0时,μ→0,y±→±1,根据勒贝格控制收敛定理,可以得到

μ→0.

即(22)式得证.

如果h→hs,那么

根据勒贝格控制收敛定理,可以得到

即(23)式得证,且所证2条极限曲线如图4所示.

图 4 光滑周期波在参数平面(T,c)中的2条极限曲线的存在区间

参考文献[14-15]可知二阶微分方程(4)的光滑周期解的波长相当于系统的周期轨道的周期.因此结合命题2.1和2.2,可以给出周期函数T(h)与对应波长函数λ(a)的图形,见图5～8.

图 5 当α<0,β>0时,周期函数T(h)的图形

图 6 当α<0,β>0时,波长函数λ(a)的图形

图 7 当α<0,β<0时,周期函数T(h)的图形

图 8 当α<0,β<0时,波长函数λ(a)的图形

3 结束语

本文研究了短脉冲方程的周期波的波长.由于文中短脉冲方程是含参数，其波长受参数影响.通过变量变换,短脉冲方程可以转化为一个平面多项式微分系统.当参数α<0时,短脉冲方程具有光滑的周期波,本文利用动力系统的定性理论和分析的方法研究这个多项式微分系统,其主要结果是给出了周期函数T(h)的单调性质.结果表明,周期函数T(h)的单调性受参数β符号的影响,β>0时,周期函数单调递减.β<0时,周期函数单调递增.此外β>0时,利用勒贝格控制收敛定理给出了周期在平衡点附近的极限值.