分次投射盖和交换分次完全环

谢雅静, 王芳贵, 吴小英

(四川师范大学 数学科学学院, 四川 成都 610066)

1 引言与预备知识

完全环的研究可以追溯到1957年Eilenberg等[1]的工作,他们引入了“极小满同态”的概念.Eilenberg[2]称一个模范畴为“完全的”,如果每个模都存在极小满同态.极小满同态也是Bass讨论的所谓投射盖[3].模范畴的完全性也就是后来学者所说的完全环.Bass证明了环R为左完全环当且仅当每一个左R-模的平坦维数与投射维数相等,等价于R/J(R)是半单环,且J(R)是左T-幂零理想,也等价于R有关于右主理想的降链条件.完全环的研究引发了许多环类的研究.例如,文献[4-5]把任意非零R-模都有极大子模的环R称为Bass环,并给出了系统的刻画.

分次环起源于代数几何学的研究发展,分次环的研究与群环、交叉积、不动子环等理论有密切联系.20世纪80年代以来,很多学者将一些重要的环类与模类的研究应用于分次环上,产生了对应的分次环类与模类，例如,分次投射模、分次半单模与分次半单环等分次模类和分次环类的基本概念,参见文献[6-7].其他分次模类与分次环类例如:文献[8]刻画了分次Gorenstein平坦模的性质,继而文献[9]讨论了Gorenstein分次投射盖的存在性.文献[10]定义(左)分次Bass环为每个非零分次(左)R-模都有极大分次子模的分次环,也给出了相应的刻画.

交换的完全环还有一些更精细的结构.例如,文献[14]得到交换完全环可以表示为有限个局部完全环的直积.本文也通过类比未分次完全环的刻画,展开对分次多余子模、分次投射盖与分次半完全环的讨论,在交换条件下给出了分次完全环的其他等价刻画.尽管未分次模范畴的许多命题在分次模范畴都有一条对应的命题,但这些对应命题的实现仍需要做好细致的转换工作.文献[15]沿用未分次情形的多余子模和投射盖的研究路线,引入和成功刻画了分次半完全环.从文献[15]的研究中可以看到该文命题2.4的证明就是一个细致转换的例子.本文为了给出分次完全环的一些等价刻画,需要改造Bass的T-幂零方法,更明确地,即改造文献[16]的定理3.10.19,使之适合于分次情形.最后也给出了是分次完全环,但不是完全环的例子.

设σ,τ∈G,令M(σ)τ=Mτσ,则

是分次模,称为M的σ-平移.

给定分次同态f:M→N,σ∈G,则f诱导同态fσ:M(σ)→N(σ),使得fσ(x)=f(x),x∈M(σ)τ,τ∈G.因此有fσ是单分次同态(或满分次同态,分次同构)当且仅当f是单分次同态(或满分次同态,分次同构).容易看到,若0→A→B→C→0是分次正合列,则诱导序列0→A(σ)→B(σ)→C(σ)→0也是分次正合列.

用Homgr(M,N)表示从M到N的分次同态的集合.尽管假设R是交换环,但Homgr(M,N)只是一个Re-模.

令HomR(M,N)σ=Homgr(M,N(σ)),则

是分次模.

用Extngr(-,-)表示Homgr(-,-)的右导出函子,令ExtnR(M,N)σ=Extngr(M,N(σ)),以及

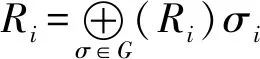
以下用R-gr表示分次R-模范畴,gr-pdRM表示分次模M的分次投射维数.相关的概念和符号,函子Hom、Ext的诸多性质,均参见文献[6-7].未分次模范畴的相关概念和符号是常规的,可参见文献[16-17].

2 分次多余子模

分次多余子模对分次投射盖的刻画极为重要,本节讨论分次多余子模的相关性质.在文献[7]中,设M是分次模,N是M的分次子模.称N为M的分次多余子模,是指对于M的分次子模U,由N+U=M能推出U=M.显然分次多余子模的分次子模仍然是分次多余子模.为了确定分次多余子模的范围,需要模的分次Jacobson根概念(参见文献[7]).设M是分次模,M的全部极大分次子模的交叫做M的分次Jacobson根,用Jg(M)表示,即

Jg(M)=∩{A|A是M的极大分次子模}.

若M无极大分次子模,则规定Jg(M)=M.

引理 2.1设M是分次模.1) 设A是M的分次子模,则A是M的极大分次子模当且仅当对任何齐次元素x∈M-A,有Rx+A=M.

2) 设x∈h(M),则Rx不是分次多余子模当且仅当存在M的极大分次子模A,使得x∉A.

证明1) 类似于未分次情形的证明.

2) 设Rx不是M的分次多余子模.令Γ是使得Rx+B=M的真分次子模B的集合.显然,当B∈Γ时,x∉B.由条件,Γ非空.由Zorn引理,Γ中有极大元A.若B是M的分次子模,且A⊂B.由于Rx+A=M,故Rx+B=M.由A的极大性,有B=M.故A是M的极大分次子模.

反之,设A是M的极大分次子模,且x∉A,则Rx+A=M,从而有A≠M.故Rx不是M的分次多余子模.

引理 2.21) 设M是分次单模,a∈Jg(R),则aM=0.

2) 设M是分次模,A是M的极大分次子模,则Jg(R)M⊆A.

证明1) 由文献[6]的引理1.7.2,存在R的极大分次理想m,以及σ∈G,使得M≅(R/m)(σ).于是M也是分次R/m-模.由于a∈m,故有aM=0.

2) 对任何a∈Jg(R),由于M/A是分次单模[6],故由1)有a(M/A)=0,从而有aM⊆A.由此得到Jg(R)M⊆A.

命题 2.3设M是分次模,N是M的分次子模.

1)Jg(R)M⊆Jg(M).

2)Jg(N)⊆Jg(M).

证明不失一般性,设M有极大分次子模.

1) 设A是M的极大分次子模,由引理2.2,Jg(R)M⊆A,由此得到Jg(R)M⊆Jg(M).

2) 设A是M的极大分次子模,若N∩A,则Jg(N)⊆A.若NA,则对任何齐次元素x∈N-N∩A,有Rx+A=M.故N=N∩M=Rx+N∩A.由引理2.1,从而有N∩A是N的极大分次子模.因此Jg(N)⊆N∩A⊆A,即有Jg(N)⊆Jg(M).

分次模范畴的自由对象称为分次自由模,即基底为齐次元素的自由模[7].

命题 2.4设{Mi}是一簇分次模,则

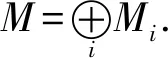
命题 2.5设M是分次模,N是M的分次子模.

1) 若N是M的分次多余子模,则N⊆Jg(M).

2) 若M的每个分次真子模包含在一个极大分次子模中,则N是M的分次多余子模当且仅当N⊆Jg(M).特别地,Jg(M)是M的分次多余子模.

证明1) 设齐次元素x∈N,则Rx是分次多余子模.若x∉Jg(M),则存在M的极大分次子模A,使得x∉A.由引理2.1,Rx不是分次多余子模,矛盾.

2) 必要性由1)即得.反之,设N⊆Jg(M).设U是M的分次子模,且N+U=M.若U≠M,由条件,存在M的包含U的极大分次子模A.由于N⊆Jg(M)⊆A,得到N+U⊆A≠M,矛盾.故N是M的分次多余子模.

推论 2.6设M是有限生成分次模,则有:

1)M一定有极大分次子模;

2) 设N是M的分次子模,则N是M的分次多余子模当且仅当N⊆Jg(M).

例 2.71) 设M是有限生成分次模.由文献[7]的定理6.3.10,当G是有限群时,有Jg(M)⊆J(M),其中J(M)是M的Jacobson根,即M的极大子模的交.特别地,当G是有限群时,Jg(R)⊆J(R),其中J(R)是环R的Jacobson根.

2) 一般来说,未必有Jg(R)⊆J(R).例如,设K是域,多项式环R=K[x]视为Z-分次环,即当n≥0时,Rn=Kxn,当n<0时,Rn=0,则J(R)=0.但(x)是R的分次多余子模,故Jg(R)≠0.这也说明了分次多余子模未必是多余子模.

命题 2.8[15]记J=Jg(R).设P是非零的分次投射模,则Jg(P)=JP≠P,从而P有极大分次子模.

3 分次投射盖

分次模M的分次投射盖在文献中常常表述为R-gr中的投射盖(参见文献[7]的推论6.3.11),即存在分次投射模P,与分次满同态φ:P→M,使得Ker(φ)是P的分次多余子模.

引理 3.1设M是分次模,P是分次投射模,φ:P→M是满分次同态,且Ker(φ)是P的分次多余子模,则有:

1) 设P1是分次投射模,g:P1→M是满分次同态,h:P1→P是分次同态,且φh=g,则h是满分次同态.

2) 若M是分次投射模,则φ是分次同构.

证明1) 设x∈P.由于g是满分次同态,故存在y∈P1,使得g(y)=φ(x)=φh(y).于是u:=x-h(y)∈Ker(φ).从而有Ker(φ)+h(P1)=P.由Ker(φ)是P的分次多余子模,有h(P1)=P,即h是满分次同态.

2) 由条件,Ker(φ)是P的直和加项,又Ker(φ)是P的分次多余子模,故Ker(φ)=0.因此φ是分次同构.

定理 3.21) 设J=Jg(R).

2) 设I是R的分次理想,且I⊆J,P是有限生成分次投射模.设π:P→P/IP是自然分次同态,则(P,π)是P/IP的分次投射盖.

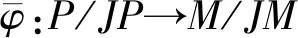
证明1) 由命题2.5,Ker(π)=IP是P的分次多余子模,故(P,π)是P/IP的分次投射盖.

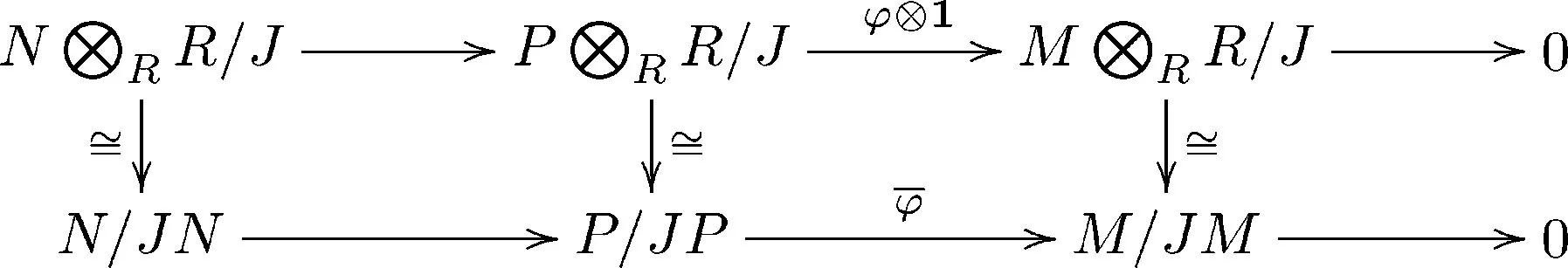
其中顶行是分次正合列,从而底行也是分次正合列.由命题2.5与命题2.8,N⊆JP,故

Im(N/JN→P/JP)=(N+JP)/JP=0,

定理 3.3设I是R的分次理想,且I⊆Jg(R).设P是有限生成分次投射模,F是有限生成分次模.

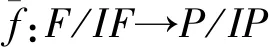
2) 若F分次投射模,且F/IF≅P/IP,则F≅P.

证明1) 由条件有下面的两行是分次正合列的交换图:

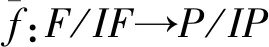
2) 设g:F/IF→P/IP是分次同构.由于F是分次投射模,故存在分次同态f:F→P,使得下图可交换:

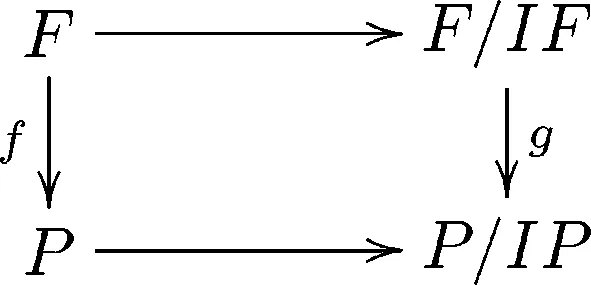
由1)有f是分次同构的.

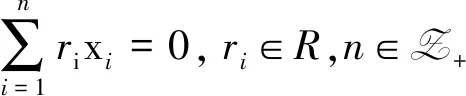
引理 3.4设I是R的分次理想,M是分次模,x,z1,…,zn∈M是一组齐次元.

1) 若有不全为零的a1,…,an∈I,使得

a1z1+…+anzn=0,

则有不全为零的齐次元b1,…,bn∈I,使得

b1z1+…+bnzn=0.

2) 若有a1,…,an∈I,使得

x=a1z1+…+anzn,

则有齐次元b1,…,bn∈I,使得

x=b1z1+…+bnzn,

且deg(bi)deg(zi)=deg(x),i=1,2,…,n.

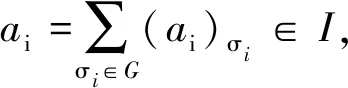
从而对任何μ∈G,只要σiτi=μ,就有

(a1)σ1z1+…+(an)σnzn=0.

因为a1,…,an不全为0,不妨设a1≠0.故存在σ1∈G,使得(a1)σ1≠0.令μ=σ1τ1,σi=μτi-1,i=2,3,…,n.再令bi=(ai)σi,i=1,2,…,n,则b1,…,bn即为所求.

2) 证明方法与1)类似的.

引理 3.5设K是分次域,M是分次K-模,则M是分次自由模.

证明不妨设M≠0.欲证M是分次自由模,只要证明M有一个由齐次元素构成的基底即可.

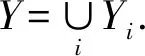
下面证明X就是M的生成系,从而M是以X为基底的分次自由模.设F是M的由X生成的分次子模,则F是M的分次自由子模.下证M=F.若不然,则存在x∈h(M),x∉F.于是x不可由X中的有限个元素线性表示.令X1=X∪{x},则对任何有限个元素x1,x2,…,xn∈X,x,x1,…,xn是线性无关的,即X1是分次线性无关的子集.事实上,若有不全为零的k,k1,…,kn∈K,使得

kx+k1x1+…+knxn=0.

由引理3.4,不妨设k,k1,…,kn都是齐次元.若k=0,则由x1,…,xn是分次线性无关得到k1=…=kn=0,这是不可能的,故k≠0,于是k是可逆元,因此有

x=-k-1(k1x1+…+knxn)∈F.

这与x∉F矛盾.于是X1是分次线性无关子集,这又与X的极大性矛盾.故M=F是分次自由模.

设M是有限生成分次模,则M的生成元可取作齐次元.

设x1,…,xn是齐次元且生成M,则称X={x1,…,xn}为M的齐次生成系.若X中删除任何一个齐次元素后都不再是M的齐次生成系,则X称为M的齐次极小生成系.回顾分次环R称为分次局部环,是指R只有一个极大的分次理想.若该唯一极大理想记作m,则也常用(R,m)来表达R是以m为唯一极大分次理想的分次局部环,此时有Jg(R)=m,且R/m是分次域(参见文献[18]的定义2.1和定理2.2).由引理3.5,每个分次R/m-模是分次自由模.

引理 3.7设(R,m)是分次局部环,M是有限生成分次模.设x1,…,xn是M的齐次极小生成系,F是以齐次元e1,…,en为基底的分次自由模.设分次同态φ:F→M,使得φ(ei)=xi,i=1,…,n,则(F,φ)是M的分次投射盖.从而分次局部环上任何有限生成分次模有分次投射盖.

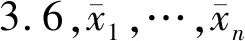
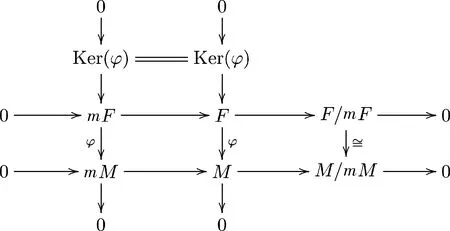
故有Ker(φ)⊆mF.由推论2.6,Ker(φ)是F的分次多余子模.从而(F,φ)是M的分次投射盖.

推论 3.8设(R,m)是分次局部环,P是有限生成分次投射模,则P是分次自由模.

证明设φ:F→P是P的分次投射盖.从定理3.7的证明过程看到,F是有限生成分次自由模.由引理3.1,φ是分次同构.因此P是分次自由模.

例 3.9由文献[7]的推论6.3.11,若G是有限群,则分次投射盖一定是投射盖.但一般来说,分次投射盖未必有投射盖.仍沿用例2.7之分次环R=K[x],则R→R/(x)是分次投射盖,但不是投射盖.

4 分次完全环

由文献[15]引入的分次半完全环的定义:若R/Jg(R)是分次半单环,且次数为e的幂等元ε模Jg(R)可以提升到R,则R称为分次半完全环.可以用齐次幂等元来代替次数为e的幂等元的说法.

引理 4.1设ε∈R是齐次幂等元,则ε∈Re.

证明设ε∈Rσ,不妨设ε≠0.由于ε=ε2∈Rσ2,有σ2=σ,故σ=e.

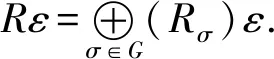
引理 4.31)R=I⊕J,其中I和J是R的分次理想,则I=Rε,J=R(1-ε),其中ε是齐次幂等元.

2) 若上面的I是分次单理想(亦称分次极小理想),则I是以ε为单位元的分次域.

证明1) 由于R=I⊕J,则可设I=Rε,J=Rε′,其中ε∈I,ε′∈J,ε和ε′是幂等元,且1=ε+ε′.记

2) 令J=R(1-ε),则J是R的分次理想,且R=I⊕J.考虑投影映射p:R→I,使得p(a+b)=a,其中a∈I,b∈J.则显然有p是分次环的满分次同态.由于I是R的分次单理想,以及I≅R/J,则J是R的极大分次理想[6].由文献[18]的定义2.1与定理2.2,因此有I≅R/J是分次域.

回顾非零的分次模M称为分次单模,是指M只有平凡的分次子模.M称为分次半单模,是指M可表示为分次单子模的直和.分次环R称为分次半单环,是指R作为R-模是分次半单模.在文献[6]中指出分次环R是分次半单环当且仅当R=L1⊕…⊕Ln,其中每个Li是R的分次单理想.若R为分次半单环,则Re是半单环[6].分次半单环也有所谓的分次版本的Weddenburn定理如下.

命题 4.4设R为分次半单环,则R≅K1×…×Kn,其中每个Ki是分次域.

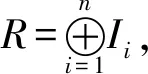
定理 4.5对于分次环R,以下各条等价:

1)R是分次半完全环;

2)R/Jg(R)是分次半单环,且R/Jg(R)中的齐次幂等元可以提升到R;

3)R有一个齐次幂等元的完全正交系ε1,…εn,使得每个εiR是分次局部环;

4)R是有限个分次局部环的直积,即R≅R1×…×Rn,其中每个Ri是分次局部环;

5) 每个分次循环模都有分次投射盖.

证明记J=Jg(R).

1)⟺2) 由引理4.1即得.

1)⟹3) 由于R/J是分次半单环,由命题4.4,可设R/J=K1×…×Kn,其中Ki是分次域.设1i表示Ki的单位元,则xi=(0,…,0,1i,0,…,0)是R/J的齐次幂等元.故存在R的齐次幂等元εi,使得εi=xi,i=1,…,n.由于i≠j时,xixj=0,故εiεj∈J∩Re=J(Re).注意J(Re)中的幂等元只有0,故εiεj=0.由此可得ε1+…+εn=1,即{ε1,…,εn}是R的齐次幂等元的完全正交系.于是R=ε1R⊕…⊕εnR.由于J=ε1J⊕…⊕εnJ,故R/J=(ε1R/ε1J)⊕…⊕(εnR/εnJ).由命题2.4,εiJ=Jg(εiR).由于εiR/εiJ≅Ki是分次域,故εiR是分次局部环.

3)⟹4)⟹2) 显然.

1)⟹5) 由文献[15]的定理3.5可得.

5)⟹1) 设x∈R/J是齐次幂等元,由假设,分次模Rx有分次投射盖.设φ:P→Rx是分次投射盖.设g:R→Rx是自然分次同态,即g(r)=rx,其中r∈R.由于x∈(R/J)e,故g是满分次同态.由引理3.1,存在满分次同态h:R→P,使得下图

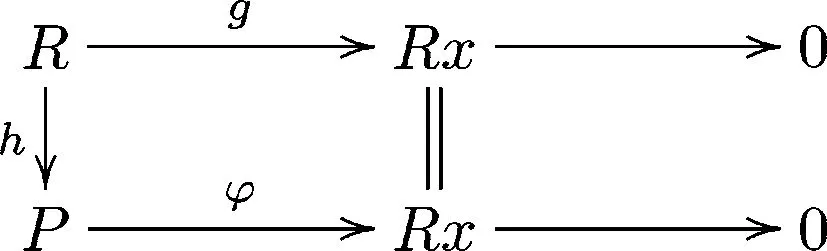
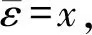
设J⊆A⊆R,则R/A是分次循环模.上面证明过程已经说明,存在齐次幂等元ε∈R,及分次同态φ:εR→R/A,使得φ:εR→R/A是分次投射盖.记I=Ker(φ),则I是εR的分次多余子模,从而I⊆Jg(εR)⊆J.于是I=εI,且

R/A≅εR/εI,Jg(εR/εI)=Jg(εR)/εI=εJ/εI.

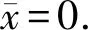
推论 4.61) 设R是分次半完全环,I是R的分次理想,则R/I也是分次半完全环.

2) 分次半单环和分次局部环都是分次半完全环.

命题 4.71) 设P是分次投射模,则对任何σ∈G,P(σ)也是分次投射模.

2) 设F是分次自由模,则对任何σ∈G,F(σ)也是分次自由模.

3) 设τ1,τ2,…,τn,…是G中的元素序列,则存在分次自由模F,其基底为x1,x2,…,xn,…,使得xn∈Fτn,n=1,2,….

证明1) 设0→A→B→C→0是分次正合列,则

0→A(σ-1)→B(σ-1)→C(σ-1)→0

也是分次正合列.于是有下面的交换图:

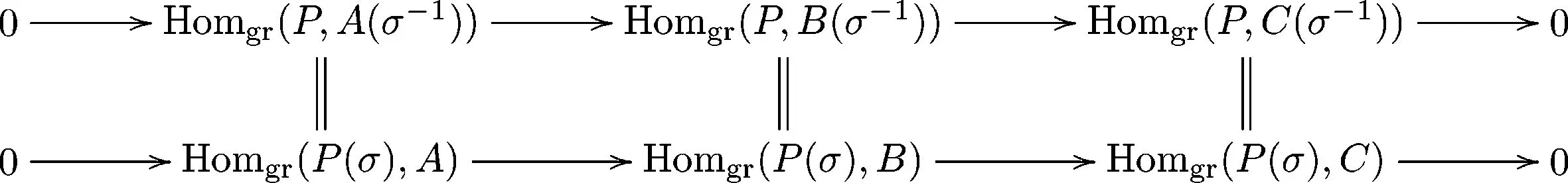
由于P是分次投射模,故顶行是正合列,因此底行也是正合列.于是有P(σ)是分次投射模.

2) 对F=R证明即可.由于R是以x:=1∈Re为基底的分次自由模,则容易看到R(σ)是以xσ:=x∈R(σ)σ-1为基底的分次自由模.

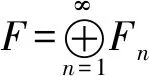
引理 4.8设a1,…,an,…是R中的齐次元素序列,deg(an)=τn.由命题4.7,存在分次自由模F,其基底为齐次元x1,…,xn,…,其次数为

令

yn=xn-anxn+1,n=1,2,…,

则y1,…,yn,…是齐次元.设K是F的由y1,…,yn,…生成的分次子模,则有:

1)K是以y1,…,yn,…为基底的分次自由模;

2) 对任何n,y1,…,yn,xn+1,xn+2,…也是F的基底;

3)K=F当且仅当对任何正整数k,存在一个n>k,使得ak…an=0;

4) 若K是F的直和项,则分次主理想降链

(a1)⊇(a1a2)⊇…⊇(a1…an)⊇…

是稳定的.

证明由引理3.4得

故yn是齐次元,且deg(yn)=deg(xn).其余部分引用文献[16]的定理3.10.19即得.

定理 4.9设J是R的分次理想,则以下各条等价:

1)J是T-幂零理想;

2)J是分次T-幂零理想,即如果a1,…,an,…是J中的任何齐次元素序列,则存在正整数m,使得a1…am=0;

3) 对任何非零分次模M,JM≠M;

4) 对任何非零分次模M,JM是M的分次多余子模;

5) 对任何分次模M,N(M):={x∈M|Jx=0}是M的分次本性子模.

证明1)⟺2) 见文献[12]的引理1.1.

1)⟹3)⟹4) 由文献[16]的定理3.10.20即得.

4)⟹2) 设a1,…,an,…∈h(J).由引理4.8,存在分次自由模F,其基底为齐次元素x1,…,xn,…,且yn=xn-anxn+1还是齐次元,n=1,2,….令K是由齐次元素y1,…,yn,…生成的分次子模.于是有F=K+JF.由假设有K=F.由引理4.8的3),J是分次T-幂零理想.

1)⟹5) 由文献[16]的定理3.10.20即得.

5)⟹2) 类似于未分次情形(参见文献[16]的定理3.10.20)的证明.

Rafael把满足分次平坦(左)R-模是(分次)投射模的条件的分次环叫做左(分)次完全环[11].定义如果每个分次R-模有分次投射盖,则称R是分次完全环.由定理4.5,显然有分次完全环是分次半完全环.在文献[12]中,设R是完全分次环(完全环又是分次环),则有R/Jg(R)是分次半单环,且Jg(R)是T-幂零理想;与每个分次平坦模是(分次)投射模是等价的.其就是分次完全环的两条等价刻画.下面为了证明分次完全环的其他等价刻画,先证明分次环R中的齐次幂等元模分次理想可以提升到R.

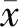
1=(x+(1-x))2n=

令

则有

于是可把e与1-e分别表示为

e=xng(x), 1-e=(1-x)nh(x).

因此

e(1-e)=xn(1-x)ng(x)h(x)=0,

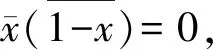
定理 4.11(分次版本的Bass定理) 对分次环R,以下各条等价:

1)R是分次完全环;

2)R/Jg(R)是分次半单环,且每个非零分次模都有极大分次子模;

3)R≅R1×…×Rn,其中每个Ri是分次局部环,且每个Jg(Ri)是T-幂零理想;

4) 对任何分次模M,有gr-pdRM=gr-fdRM;

5)R有关于分次主理想的降链条件;

6) 每个分次模有关于分次循环子模的降链条件;

7)R/Jg(R)是分次半单环,且任何非零分次模有分次单子模.

证明令J=Jg(R).

1)⟹2) 设R是分次完全环.由定理4.5,R/J是分次半单环.设M是非零分次模,f:P→M是分次投射盖,记K=Ker(f).由命题2.8,P有极大分次子模A.由于K是P的分次多余子模,故K⊆A,因此f(A)就是M的极大分次子模.

2)⟹3) 设M是非零分次模.由条件,M有极大分次子模,因此有JM≠M.由定理4.9,J是T-幂零理想.又R是交换环,则J也是诣零理想.由引理4.10,齐次幂等元关于J可以提升,因此R是分次半完全环.于是有R≅R1×…×Rn,其中每个Ri是分次局部环.从而每个Jg(Ri)是T-幂零理想.

3)⟹1) 由条件,可设R是分次局部环,且J是T-幂零理想,也是R的唯一的极大分次理想.设M是非零分次模,由引理3.5,M/JM是分次域R/J上的分次自由模.故存在分次自由模F,使得F/JF≅M/JM.因此存在分次同态g:F→M,使得下图可交换:

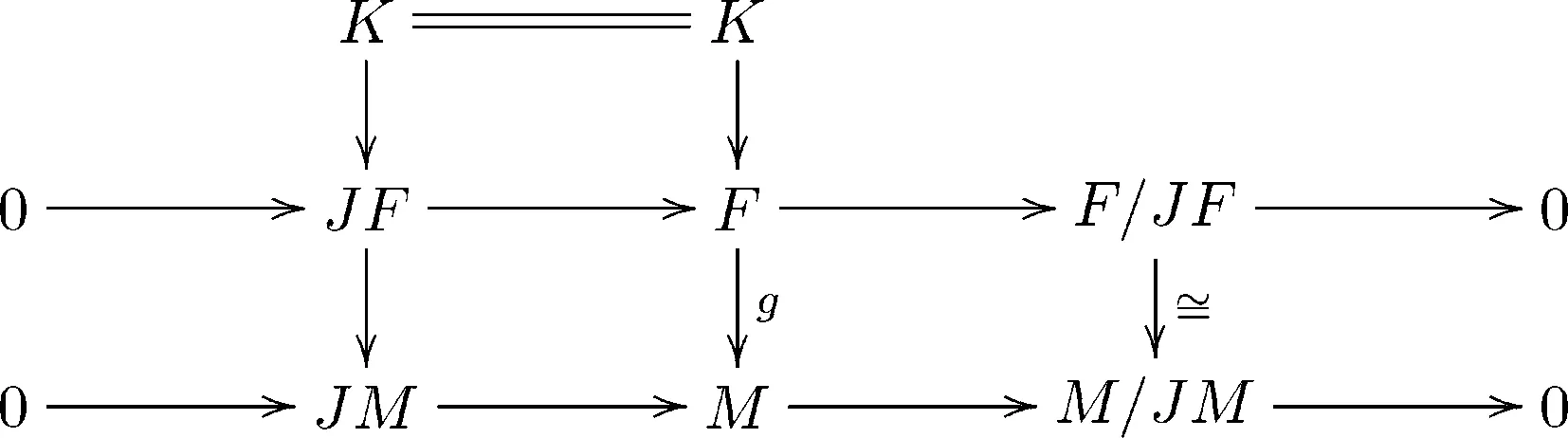
于是有g(F)+JM=M.由于J是T-分次幂零理想,由定理4.9,JM是M的分次多余子模.从而有g(F)=M,即g是满分次同态.由于K:=Ker(g)⊆JF,从而K是F的分次多余子模,故F→M是M的分次投射盖.于是得到R是分次完全环.

1)⟺4) 由文献[12]的引理1.2易得.

4)⟹5) 由条件,显然有分次平坦模是分次投射模.R的分次主理想降链可以表示为

(a1)⊇(a1a2)⊇…⊇(a1…an)⊇…,

其中a1,…,an∈h(R),构造分次模F与K如同引理4.8,证M=F/K是分次平坦模,从而M是分次投射模,K是F的直和项.再次引用引理4.8,得到该降链是稳定的.

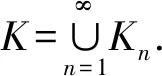
5)⟹6) 设M=Rx是分次模.则x是齐次元素.若M有不稳定的分次子模降链Rx⊃Ra1x⊃Ra1a2x⊃…,则每个ai是齐次元.由于对应有R的不稳定的分次主理想降链R⊃Ra1⊃Ra1a2⊃…,这与假设矛盾.

6)⟹7) 先证明任何非零分次模有分次单子模,不妨设M=Rx是分次循环模.如果M无分次单子模,则M有一个非零的分次真子模Ra1x.由于Ra1x也没有分次单子模,故Ra1x也有一个非零的分次真子模Ra1a2x.如此下去,得到M的分次子模降链Rx⊃Ra1x⊃Ra1a2x⊃…,这与假设矛盾.因此,M有分次单子模.

欲证R/J是分次半单环,由于R/J也有给定的性质,于是不妨设J=0.由条件,R有分次单子模I1.记I1=Rx,x∈h(R),令m1=ann(x),则m1是R的极大分次理想.由于Jg(R)=0,故m1∩I1=0,因此有R=I1⊕m1.若m1≠0,则m1有分次单子模I2,对应又得到R=I2⊕m2,以及R=I1⊕I2⊕(m1∩m2).若m1∩m2≠0,则继续前面的做法,如此下去.由于每次得到的m1∩…∩mk都是R的直和加项,从而是R的分次主理想.于是有R的分次主理想降链m1⊃m1∩m2⊃…⊃m1∩…∩mk⊃….由条件此过程不能无限进行下去,故存在n,使得m1∩…∩mn=0,从而R=I1⊕…⊕In是分次半单环.

7)⟹1) 设M是非零分次模,令N=N(M)如定理4.9.说N包含了M的全部分次单子模.事实上,设H是M的分次单子模,由文献[6]的引理I.7.2,存在σ∈G,使得H≅(R/m)(σ),其中m是R的极大分次理想.因此JH=0,故H⊆N.设X是M的任何非零分次子模,由条件,X有分次单子模,因此N∩X≠0.故N是M的分次本性子模.由定理4.9,J是T-分次幂零理想.

文献[13]证明了若R是有有限支集的分次环,则R是(左)分次完全环当且仅当Re是(左)完全环.下面给出R是强分次环的条件下R与Re的关系.

证明由于R是分次完全环,则R/Jg(R)是分次半单环,因此(R/Jg(R))e为半单环.由文献[6]的推论2.9.3,Jg(R)∩Re=J(Re),从而

(R/Jg(R))e=(Re+Jg(R))/Jg(R)≅

Re/Jg(R)∩Re=Re/J(Re)

为半单环.

由Jg(R)是T-幂零理想,以及J(Re)⊆Jg(R),所以J(Re)是T-幂零理想.从而Re为完全环.

当G是有限群时,文献[19]的引理2.1证明了M是分次投射R-模当且仅当Me是投射Re-模.其实,这一结论对任何群G都是成立的.

引理 4.13设R是强分次环,M是分次模,则有:

1)M是分次投射R-模当且仅当Me是投射Re-模;

2)M是分次平坦R-模当且仅当Me是平坦Re-模.

证明1) 设N是分次模,由Dade定理(见文献[7]的定理3.1.1),则有自然同构

故若Me是投射Re-模,必有Extngr(N,M)=0,从而M是分次投射R-模.

反之,设M是分次投射R-模.对任何Re-模I,令N=R⊗ReI,则Ne=I.因此有

故Me是投射Re-模.

2) 设M是分次平坦R-模.设Q是任何有限表现Re-模,f:Q→Me是Re-同态,则P=R⊗ReQ是有限表现分次R-模,g=1⊗f:P→M是分次同态,且Pe=Q.由文献[8]的命题2.1,存在有限生成分次投射R-模F,使得g=αh,其中α:F→M与h:P→F是分次同态.于是Fe是有限生成投射Re-模,且αe:Fe→Me与he:Pe→Fe满足αehe=f.由文献[20]的定理4.32,Me是平坦Re-模.

反之,设Me是平坦Re-模.设P是有限表现分次模,g:P→M是分次同态:则ge:Pe→Me是同态.仍由文献[20]的定理4.32,存在有限生成投射Re-模Q,以及Re-同态h0:Pe→Q,f0:Q→Me,使得ge=f0h0.令F=R⊗ReQ,则F是有限生成分次投射R-模,且Fe=Q.由Dade定理,有Homgr(P,F)=HomRe(Pe,Fe),且

Homgr(F,M)=HomRe(Fe,Me).

故存在h∈Homgr(P,F)与f∈Homgr(F,M),使得h|Pe=h0,且f|Fe=f0.由于

Homgr(P,M)=HomRe(Pe,Me),

故有g=fh.仍由文献[8]的命题2.1,M是分次平坦R-模.

定理 4.14设R是强分次环,则R是分次完全环当且仅当Re是完全环.

证明必要性由定理4.12即得,下证充分性.

设M是分次平坦模,由引理4.13的2),Me是平坦Re-模.由于Re是完全环,故Me是投射Re-模.由引理4.13的1),M是分次投射R-模.由定理4.11,R是分次完全环.

例 4.15分次完全环未必是完全环.例如,设F是域,罗朗多项式环R=F[x,x-1]为强Z-分次环.由定理4.14,R为分次完全环.注意完全环的Krull维数为0(参见文献[16]的推论3.10.23),而dim(R)=1,故R不是完全环.