泊松比对低温点火下装药结构完整性分析*

孙俊丽，龙达峰，王志军，李照勇

(1 中北大学机电工程学院，太原 030051； 2 惠州学院，广东惠州 516007；3 晋西工业集团有限责任公司防务装备研究院，太原 030027)

0 引言

端羟基聚丁二烯(HTPB)复合推进剂是目前大口径固体火箭发动机中应用最多的复合推进剂，通常采用贴壁浇注、高温固化的方式装入发动机壳体内，需要有固化降温过程。由于发动机燃烧室、包覆层、药柱之间热膨胀系数不同，大幅温度的变化会造成药柱内部及粘结界面形成热应力及热应变，壳体的变形也会引起药柱的应变，从而使内孔表面产生拉应力，在各粘接面上产生剪切应力[1]。因此装药结构完整性主要受温度载荷及点火升压载荷的影响，特别是低温环境下的装药结构完整性尤为严酷。在进行发动机装药结构完整性分析时，泊松比是药柱材料本构方程和应力应变分析的重要参数。由于推进剂在生产中会有不同的批次差异以及测量误差，造成不同批次装药的性能参数具有一定的散布范围[2]，泊松比范围在0.49～0.50之间，先前的文献表明当泊松比分别取值为0.49和0.50时，药柱的等效应变会差别到7倍以上[3-4]。泊松比的微小变化对于药柱内危险部位的应力应变会有十分明显的影响[5-6]。在工程应用中，受测量技术水平限制，粘弹性泊松比试验大多采用了弹性材料的测量方法[7]，比如常用的固体推进剂等粘弹性材料泊松比的测量标准采用GJB770B—2005[7]和QJ3228—2005[8]。粘弹性泊松比试验获取通常结合测试结果和经验综合选定[9]。文中针对采用新型四组元HTPB复合推进剂的某固体火箭发动机装药进行完整性分析，由于该装药参数泊松比是在装药固化后很短的时间内用方坯加工试样进行测量所得，但装药经固化降温到成型后，经过几个月的贮存后进行样机低温鉴定试验，分析发现随松弛载荷时间的增加，泊松比会逐渐增大，存在测量误差的泊松比并不能准确表征低温工作环境条件下的药柱实际性能，对发动机的完整性分析结果产生很大影响。因此研究在低温环境条件下泊松比的如何合理选取，在此基础上进行泊松比对低温点火下该装药结构完整性的影响分析。

1 发动机装药本构模型推导

1.1 粘弹性材料本构方程

HTPB复合推进剂是一种粘弹性材料，其单轴本构关系可以用松弛积分形式来表示：

(1)

式中E(t)为单轴松弛模量，其可用Prony级数形式表示：

(2)

对于三轴应力状态，材料内部应变主要由弹性应变{εe}和粘性应变{εc}组成，可以表示为[10]：

{ε}={εe}+{εc}

(3)

若假设推进剂是均匀和各向同性的粘弹性材料，其应力可以表示为：

(4)

需要说明的是，式(4)中{σ}与{εe}+{εc}体现为松弛积分型线粘弹性本构关系，需要其转为结构静力学的增量型本构关系，为方便有限元法求解。

在各个离散时间的每个时刻t0,t1,…，tm，若时间间隔划分得充分小，可以由公式(4)得到tm时刻的应力公式为：

(5)

式(5)中{Δεe}k={Δεe(tk)}-{Δεe(tk-1)}，{Δεc}k={Δεc(tk)}-{Δεc(tk-1)}。因此，在充分小Δtk+1=tk+1-tk的时间内，其总应力增量为：

{Δσ}k+1={σ}k+1-{σ}k

(6)

弹性应力增量为：

{Δσ}k+1=E0[ED]-1{Δεe}k+1

(7)

因此，由式(5)得到其松弛应力增量为：

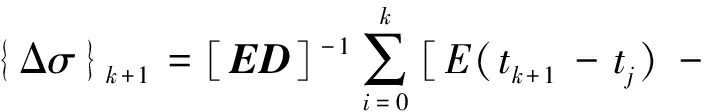
(8)

再由式(3)和式(7)可整理得到结构静力学的增量型本构方程为：

[Δσ]k+1=E({Δε}k+1-{Δεe}k+1)

(9)

式中E=E0[ED]-1为弹性矩阵。

因此，我们可推导得到在tk+1时刻的材料总应力{σ}k+1和总应变{ε}k+1分别为：

(10)

1.2 发动机装药热传导模型

考虑到固体推进剂为各向同性热流变简单材料，在分析发动机装药从固化降温直至保低温的温度传导时，将HTPB复合推进剂承受热载荷的过程视为一个没有内部热源的瞬态热传导方式，其热传导方程可以表示为[11]：

(11)

式中：T、ρ、c、λij分别表示温度、质量密度、比热容和导热系数。

采用ABAQUS软件有限元法进行热传导分析时，需要在空间域中对单元内温度场进行离散处理：

(12)

式中：Te为单元温度；Ti为节点温度；Ni为插值形函数。

采用两点差分格式在时间域内进行离散处理：

(13)

式中：Δt为离散时间间隔；α为松弛因子。

将单元内温度场离散公式(12)代入式(11)等价的泛函表达式，可得到单元的温度场离散化后的热传导平衡方程为：

(14)

将式(13)代入式(14)，由此可以整理得到HTPB复合推进剂热传导方程为：

(C+σΔtK){T}t=(C-(1-σ)ΔtK){T}t-Δt

(15)

式中：C为整体的热容矩阵；K为整体的热传导刚度矩阵。文中采用式(15)来描述发动机装药的热传导模型。

2 发动机有限元模型

2.1 装药模型

对某远程固体火箭发动机圆孔药柱进行结构完整性分析，药柱长2 000 mm，长径比为5.8，装药内孔为φ93 mm，装药剖面图如图1所示。

图1 装药剖面图

2.2 材料参数与本构模型

该模型中主要涉及到5种材料，其中发动机壳体、绝热层、释放罩和包覆层为弹性材料，HTPB复合推进剂为各向同性粘弹性材料，各材料具体参数如表1所示。

考虑到HTPB推进剂的泊松比(0.49～0.50)会随贮存时间发生明显变化，其泊松比并不能准确表征低温工作环境条件下的药柱实际性能，实际泊松比的微小变化会对HTPB推进剂装药完整性分析结果产生很大影响。因此，根据测试结果和经验取不同泊松比进行仿真分析，研究在低温环境条件下泊松比的如何合理选取，在此基础上进行了泊松比对低温点火下该装药结构完整性的影响分析。HTPB推进剂采用粘弹性本构模型，按计算公式(2)，基于实测装药参数拟合得到8阶Prony级数松弛模量为：

(16)

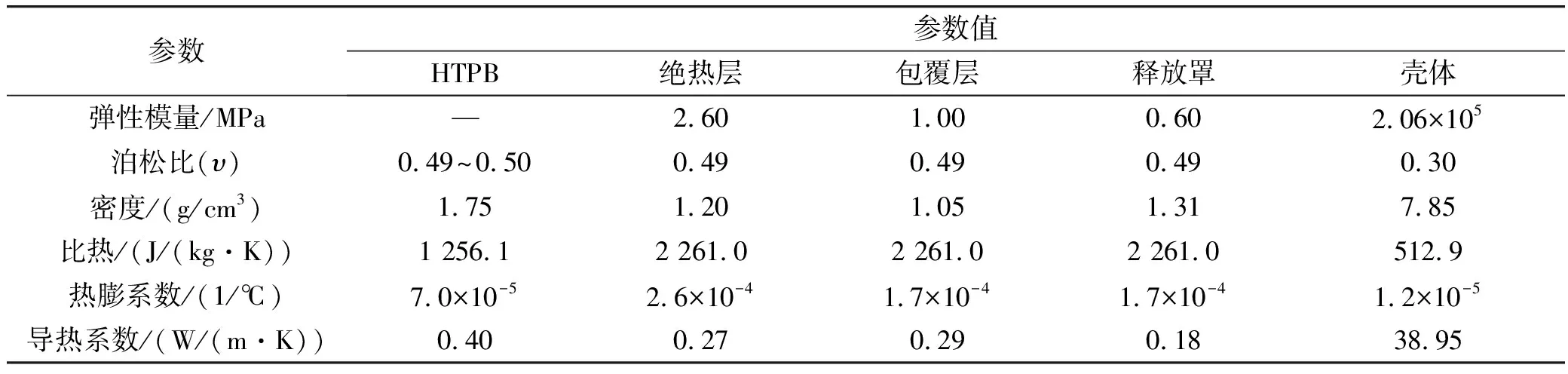
表1 材料参数

由实测数据拟合得到其时温等效模型为：

(17)

式中：C1=5.058 52，C2=172.107 62，T0=20 ℃。从而计算可得T=50 ℃时，αT=0.177 4；T=20 ℃时，αT=1；T=-45 ℃时，αT=117 4.48。

2.3 网格与载荷设置

为简化计算，根据药柱对称特征选取其1/2模型作为研究对象，模型划分采用六面体结构化网格，生成的网格模型如图2所示，共划分165 296个单元。药柱的温度与压力载荷设置：

1)固化降温：模拟装药的固化降温过程，装药固化温度为50 ℃，零应力温度为58 ℃，经10 h自然冷却到常温20 ℃，继续保持恒温20 ℃以确保发动机内温度基本平衡，经40 h后完成装药固化。

2)常温点火：模拟发动机的常温工作，装药低温20 ℃保持48 h，然后发动机内部施加0～14 MPa压强载荷，呈线性变化，作用时间为0.1 s。

3)低温点火：模拟发动机的低温工作，装药低温-45 ℃保持48 h，然后发动机内部施加0～13 MPa压强载荷，呈线性变化，作用时间为0.1 s。

图2 网格模型

3 计算结果分析

按上述推导所得发动机装药本构模型、仿真方法和载荷条件等进行泊松比(υ)对发动机装药结构完整性分析。针对在低温和常温环境两种不同的条件下，选取不同的泊松比(0.49～0.50)进行了该发动机装药结构完整性的影响分析。在进行完整性仿真时，首先按2.3所述的1)固化降温和3)低温点火条件进行温度载荷设置，用来模拟发动机最为恶劣的低温工作环境。图3所示为经过固化降温到保低温最终时刻的装药温度云图，图中左侧颜色图例表征为温度值。

图3 降温至-45 ℃时装药温度云图

从结果来看，药柱的最终温度稳定在-44.74～-44.99 ℃之间，达到低温工作环境。然后，选取泊松比为0.491，对该发动机装药结构先后分别施加温度和压强载荷进行装药结构完整性分析，仿真结果如图4和图5所示，其中图4所示为装药结构施加温度载荷所得响应结果，图5所示为装药结构施加压力载荷所得响应结果，图中左侧颜色图例表征其等效应变值。

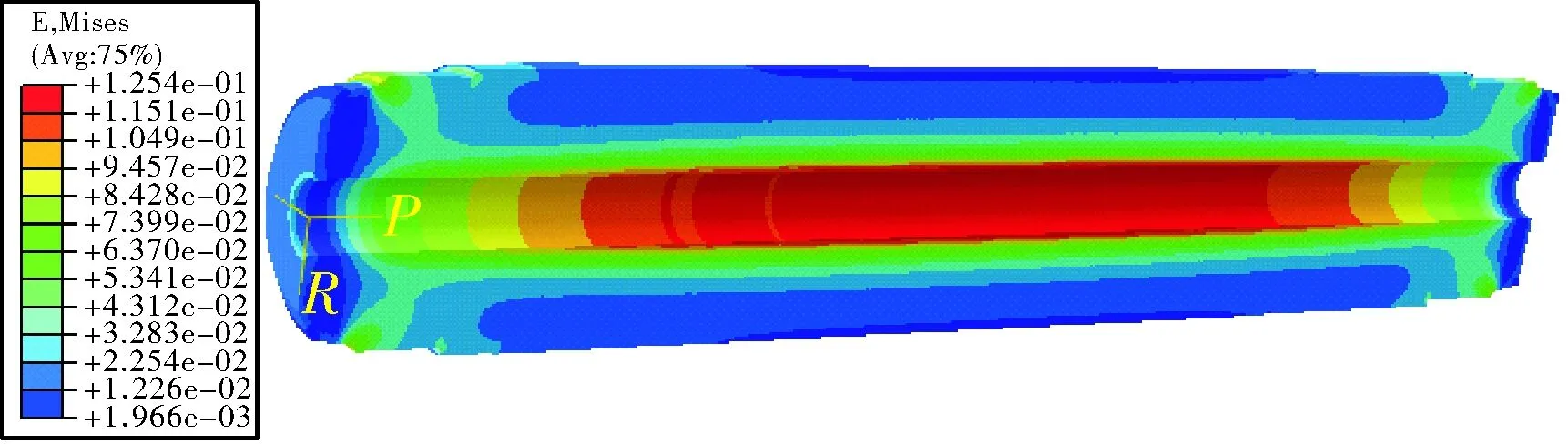
图4 温度载荷等效应变云图(υ=0.491)

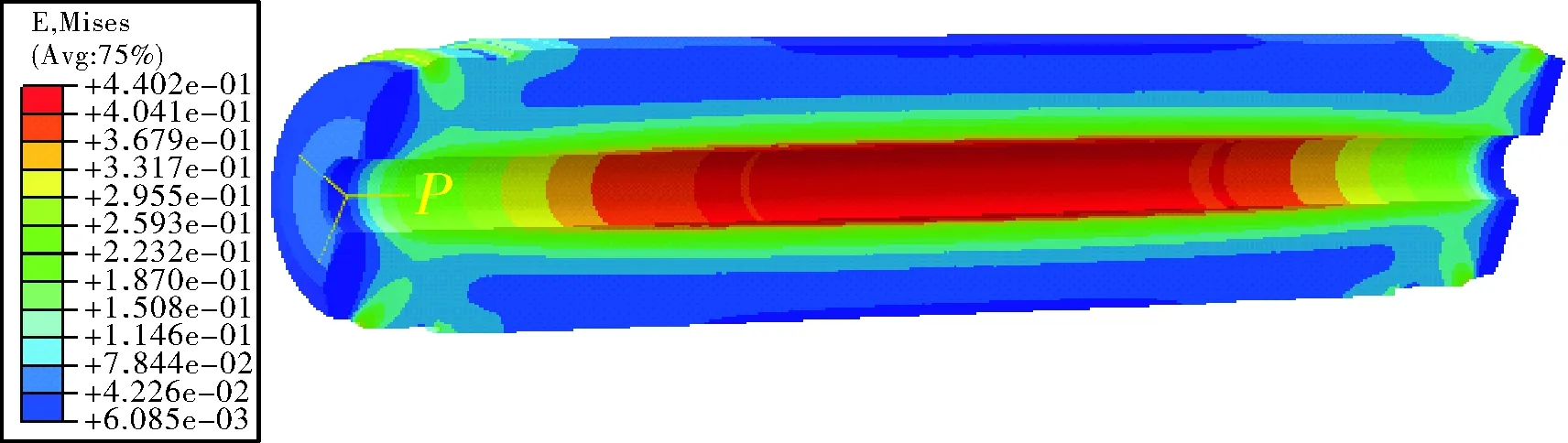
图5 压强载荷等效应变云图(υ=0.491)

图4所示可知其温度载荷最大等效应变为12.54%，从图5所示可知，受压强载荷后的最大等效应变位置出现在药柱中段，最大值为44.02%，等效应变从内孔中间到两端逐渐递减为0.61%，为了便于观察内孔等效应变情况，在药柱内孔处规划路径path-1如图6所示，可以清楚看到内孔等效应变变化曲线；如图7所示，药柱的最大等效应变出现在药柱中段，药柱两端粘接应力释放罩端的等效应变较大。

图6 药柱内孔处规划路径path-1

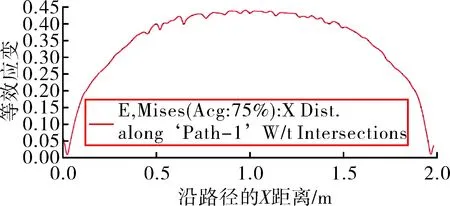
图7 规划路径path-1的等效应变

可计算得到该发动机低温安全系数为0.92，在工程上看该装药结构为不完整。图8～图13所示为泊松比分别取值为0.495、0.497和0.499时该发动机装药结构完整性分析结果。

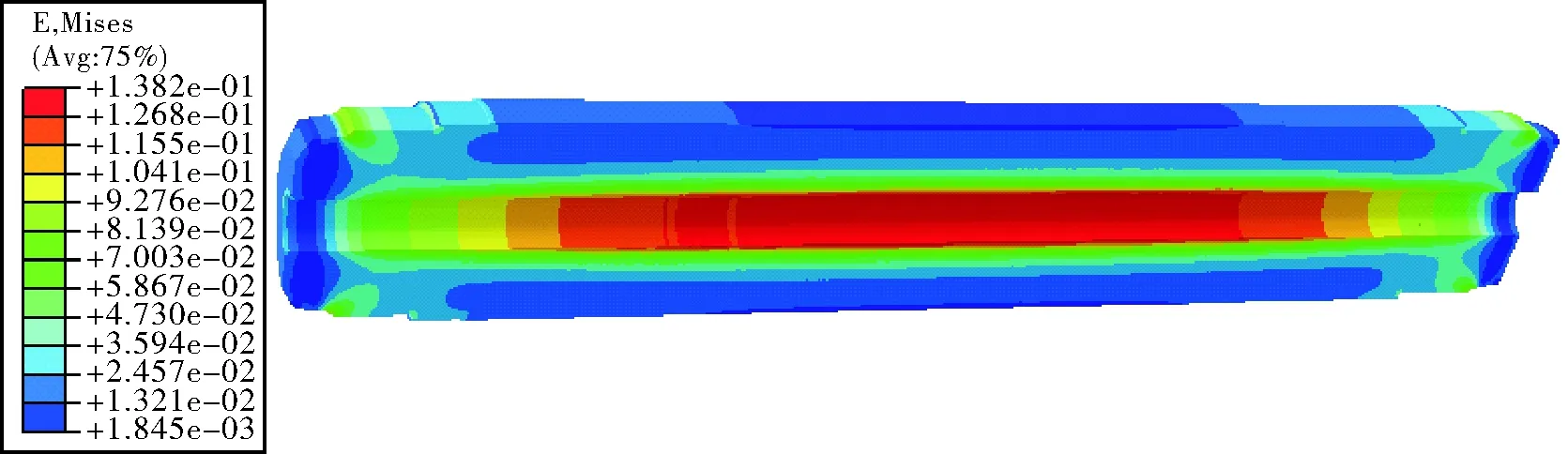
图8 温度载荷等效应变云图(υ=0.495)

图9 温度载荷等效应变云图(υ=0.497)

图10 温度载荷等效应变云图(υ=0.499)

图11 压强载荷等效应变云图(υ=0.495)

图12 压强载荷等效应变云图(υ=0.497)

从上述结果可知，低温点火下泊松比分别为0.495、0.497和0.499时该装药结构承受温度载荷后的最大等效应变分别为13.82%、14.56%和15.37%，而受压强载荷后的最大等效应变分别为35.44%、30.47%和24.96%，由此计算得到各安全系数分别为1.14、1.33和1.62。此外，为了对比常温工作状态，还进行常温下不同泊松比对装药结构完整性分析，因篇幅所限不再罗列云图，两种情况下的仿真结果对比如表2所示。

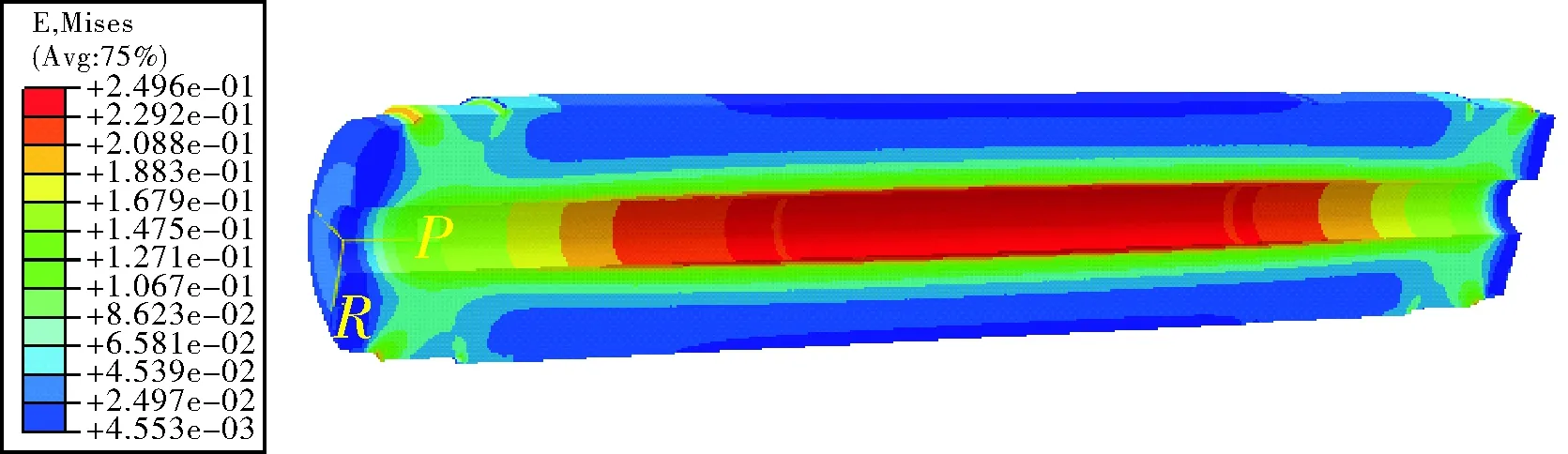
图13 压强载荷等效应变云图(υ=0.499)

υ常温环境低温环境εm,T/%εm,P/%εm,T/%εm,T/%n0.4915.1239.0012.5444.020.920.4925.2336.6512.8442.030.960.4935.3634.1813.1539.931.010.4945.4931.6013.4837.741.070.4955.6228.8813.8235.441.140.4965.7726.0314.1833.021.220.4975.9223.0314.5630.471.330.4986.0719.8714.9627.791.450.4996.2416.5415.3724.961.62

注：υ为泊松比，εm,T为受温度影响的最大等效应变，εm,P为受压强影响的最大等效应变，n为安全系数。

根据表2仿真计算所得数据，可以得到受温度和压强载荷作用下药柱最大等效应变随泊松比变化的关系曲线分别如图14和图15所示。

图14 温度载荷最大等效应变与随泊松比的变化曲线

从图14结果来看，该发动机装药温度载荷等效应变在低温环境下影响较大；从图15所示曲线中可知，泊松比也在低温下的装药结构完整性分析结果影响较为明显，压强载荷最大等效应变随泊松比增大而减小，整体上是呈线性反比例关系。实际上，对该装药方坯加工试样进行测量所得低温延伸率为40.5%。从仿真结果来看，当泊松比取值为0.493时，计算所得到压强载荷最大等效应变为39.93%，其所对应装药延伸率近似40.5%，由此可知在低温环境下该装药结构泊松比选取为0.493最为合理，此时该装药的低温安全系数为1.01，表明该发动机装药结构也基本完整。

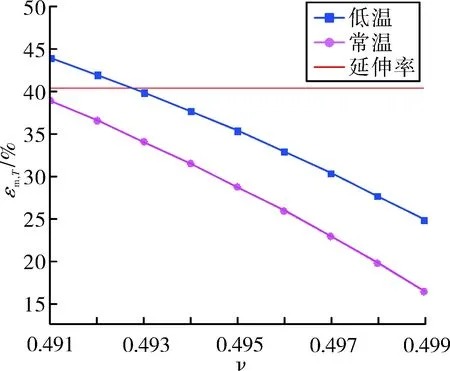
图15 压强载荷最大等效应变与随泊松比的变化曲线

4 结论

文中对某固体火箭发动机药柱进行了泊松比对低温点火下装药结构完整性的影响分析。针对该装药结构重点分析在温度和压强载荷下的等效应变、低温环境条件下泊松比的如何合理选取以及发动机的低温安全系数问题。分析结果表明，该发动机装药的温度和压强载荷等效应变在低温环境下影响较大，温度载荷等效应变随泊松比的增大而增大，而压强载荷最大等效应变随泊松比增大而减小，整体上是呈线性比例关系。通过分析发现，该装药结构在低温点火环境下泊松比选取为0.493最为合理，此时发动机低温安全系数为1.01，该发动机装药结构基本完整。很明显在分析大口径、大长径比发动机装药结构完整性时，应根据测试及经验对参数泊松比在不同温度下分别取不同的值，整体上泊松比随着温度升高的趋势，取值应逐渐微小增加。