基于霍普金森压杆的高g值加速度发生器的改进*
2019-11-13高嘉诚范锦彪
高嘉诚,范锦彪,王 燕
(中北大学仪器科学与动态测试教育部重点实验室,太原 030051)
0 引言
在现代战争中,火炮和战斗部的最大毁伤已经成为全世界的研究热点,在火工品和侵彻等研究领域,高g值加速度发生器已经成为了主要的研究器件。
随着近年来国防技术的不断发展,战斗部和火工品的毁伤效果逐渐增强,量程在几万个g的过载已经不能满足现在的实验需求,各种改进的高g值加速度发生器应运而生。高g值加速度发生器主要是利用自由式霍普金森杆装置实现[1-2],最近几年国内外科研人员采用霍普金森压杆技术来标定高g值加速度传感器[3-4],在标定加速度传感器时需要理想的加速度峰值和脉宽,周广宇等在研究基于自由式霍普金森杆的高g值加速度发生器的子弹和整形器方面有很大进展[5],所研究的梭形子弹在不减小加速度峰值的情况下可以获得更理想的加速度脉宽。西北工业大大学袁康博等人利用双炮管发射装置和自由式霍普金森杆来实现对加速度峰值和脉宽的控制[6],从而更好的模拟火工品和战斗部的实测环境,霍普金森压杆的波形整形技术是控制加速度峰值和脉宽的根本,加速度的峰值和脉宽又决定了火工品的安全性能和高g值加速度发生器的标定精度。
文中针对自由式霍普金森压杆的高g值加速度发生器的波形整形做出改进,针对火工品试件的安全要求,通过数值模拟仿真技术,将传统发生装置圆柱形子弹形状改为双锥形子弹,研究子弹对加载波形的影响。
1 试验装置
采用自由式霍普金森压杆作为高g值加速度发生器的试验装置,如图1所示。
由图1可知双锥形子弹撞击霍普金森压杆[7],应力波沿压杆轴向传播至试件,试件用黄油紧密吸附压杆末端,试件通过红外激光测速装置,穿过两道平行回路光束,测速装置测得试件的加速度信号转换为电压信号存储在存储示波器中,最后试件被回收箱回收。
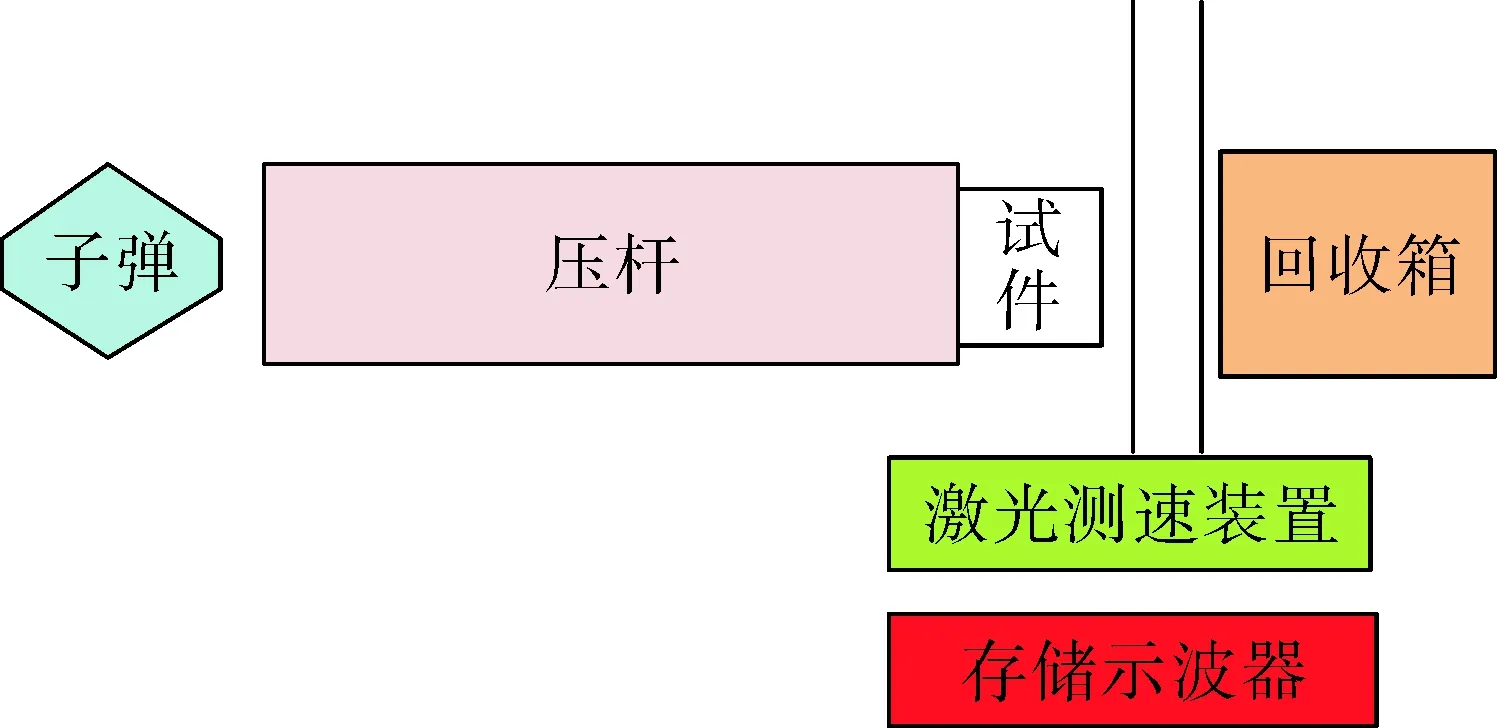
图1 高g值加速度装置示意图
2 仿真模拟
2.1 仿真模型
文中主要采用ANSYS-DYNA有限元分析软件对高g值加速度发生器进行建模仿真[8]。因为实验装置都是关于轴对称,所以采取四分之一建模方式建模。如图2、图3所示分别为双锥形子弹撞击压杆的1/4横截面示意图和仿真模型图。

图2 双锥形子弹撞击压杆1/4横截面示意图

图3 仿真模型图
图2中红色部分为双锥形子弹,绿色部分为压杆,蓝色部分为待测试件,子弹、压杆、试件均采用sweep网格划分方式划分,因为子弹沿x轴负方向以30 m/s速度撞击压杆,有限元分析最好将网格划分成长宽高相同的正方体,这样在不考虑弥散效应的前提下,压杆中的应力传播方向是水平的。图3所示仿真模型,蓝色端为子弹,紫色部分是压杆,压杆末端为试件。
2.2 材料的本构模型和参数
压杆子弹和试件均采用线性弹性材料模型[9],具体参数如表1所示。

表1 压杆子弹试件材料参数
表1是子弹压杆试件的材料模型参数,选用弹性钢材作为材料。
3 仿真结果与分析
选择直径为29 mm,长1.5 m的细长杆作为压杆,试件直径20 mm,长10 mm,子弹采用双锥形子弹,子弹几何图形如图4所示。

图4 双锥形子弹几何图形
仿真实验给双锥形子弹施加水平方向-30 m/s的初始速度撞击直径为29 mm、长为1.5 m的压杆,试件获得加速度。选取不同尺寸的双锥形子弹,得到试件的加速度-时间曲线进行比较分析。
3.1 双锥形子弹中间段直径D2对试件加速度-时间曲线的影响
改变双锥形子弹中间段直径的大小,分别选取中间段直径D2为29 mm、35 mm、40 mm,撞击端面直径D1和末端直径D3都为29 mm,子弹长度L为60 mm的子弹外形,均以-30 m/s速度撞击压杆,得到试件的加速度脉冲如图5所示。

图5 使用不同双锥形子弹中间段直径得到试件的加速度-时间曲线
由图5可以看出:不同中间段直径的双锥形子弹以相同速度撞击压杆,中间段直径最大的C形双锥形子弹获得的加速度峰值最高约为3.3×105g,中间段直径最小的圆柱形子弹A撞击,试件获得的加速度最小为2.78×105g,B形双锥形子弹直径介于A形和C形之间,B形双锥形子弹撞击后试件的加速度为3.1×106g[4],试件的加速度脉宽相同。
3.2 双锥形子弹撞击端面直径D1对试件加速度-时间曲线的影响
选取3种撞击端面直径D1分别为23 mm、26 mm、29 mm,中间段直径D2均为20 mm,末端直径为29 mm双锥形子弹,得到试件的加速度-时间曲线如图6所示。

图6 使用3种不同撞击端面直径的双锥形子弹的试件加速度-时间曲线
由图6可知使用撞击端面直径为29 mm的双锥形子弹F,试件的加速度峰值最高约为3.3×105g,使用撞击端面直径最小为23 mm的双锥形子弹D,试件得到的加速度峰值最小为2.9×105g,根据图6所示可以得到结论:以相同速度-30 m/s射出子弹,随着子弹撞击端面直径的增加,试件获得的加速度峰值越高,试件的加速度脉宽不变。
3.3 双锥形子弹长度L对试件加速度-时间曲线的影响
选取3种不同弹长L的双锥形子弹,分别取弹长为40 mm、50 mm、60 mm,撞击端面直径D1和末端直径D3均为29 mm,中间段直径D2为20 mm,均以-30 m/s撞击压杆,得到试件在3种不同弹长的双锥形子弹的作用下的加速度-时间曲线如图7所示。
由图7可知G形双锥形子弹弹长60 mm时,得到试件的加速度峰值为3.3×105g,当采用50 mm弹长的I形双锥形子弹时,试件的加速度峰值约为3.233×105g,采用40 mm弹长的H形双锥形子弹时,试件的加速度峰值为3.1×105g。
3.4 双锥形子弹末端直径D3对试件加速度-时间曲线的影响
选取3种末端直径D3分别为29 mm、26 mm、23 mm的双锥形子弹,得到试件的加速度-时间曲线如图8所示。
由图8可知,选择末端直径29 mm的L形双锥形子弹时,试件的加速度峰值最高达到3.29×105g。选择末端直径26 mm的K形双锥形子弹时,试件获得的加速度峰值为3.25×105g。选择末端直径23 mm的J形双锥形子弹时,试件的加速度峰值为3.225×105g,随着双锥形子弹末端直径的增加,试件获得的加速度峰值略有增加,试件的加速度脉宽不变。
3.5 不同几何形状的双锥形子弹以相同速度撞击,试件获得的加速度峰值比较
12种不同外形子弹撞击压杆,试件加速度峰值如表2所示。
由表2可知,1组仿真实验3种几何尺寸的双锥形子弹A、B、C,通过改变中间段直径,试件的最大加速度峰值为3 302 238 m/s2,1组的增值比算法为:(最大值-最小值)/最小值×100%,1组的增值比为18.3%。2组仿真实验采取改变撞击端面直径的方式改变试件的加速度峰值,2组试件的加速度峰值为3 293 665 m/s2,增值比为14.5%。3组改变双锥形子弹长度,3种双锥形子弹作用下试件的加速度峰值最大为3 309 701 m/s2,3组增值比为7.7%。4组选择3种不同尾部直径的双锥形子弹,试件最大加速度峰值为3 293 532 m/s2,4组的加速度峰值增值比为2.12%。由表2得到结论,通过改变双锥形子弹撞击端面直径和中间段直径对试件加速度峰值的改变很大,改变双锥形子弹的弹长和尾端直径对试件加速度峰值的改变较小。
4 理论验证
对以上2、3、4组仿真数据进行拟合分析,用Matlab将2组的撞击端面直径,3组弹长,4组尾段直径和相对应的试件的加速度峰值进行拟合。如图9~图11所示。
上述3组数据的仿真和拟合对比发现,仿真数据和拟合数据基本吻合,图9、图10、图11的拟合公式分别为式(1)、式(2)、式(3)。
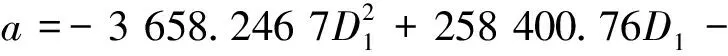
(1)
a=-464.917 9L2+58 011.765L+
1 486 830.88
(2)
a=69.132D3+7 806.63D3+
3 009 001.74
(3)
根据拟合式(1)、式(2)、式(3)可知通过改变双锥形子弹弹长和撞击端面直径可以有效提高试件加速度的峰值,试件的加速度峰值基本可以达到3.3×106g,而改变双锥形尾端直径对试件加速度峰值改变不明显。
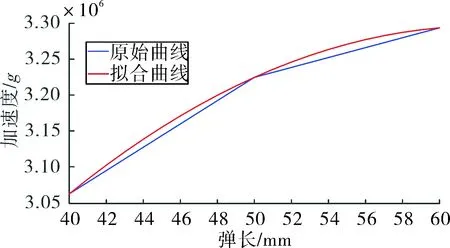
图10 子弹不同弹长试件加速度峰值的仿真和拟合对比

图11 子弹不同末端直径试件加速度峰值的仿真和拟合对比
5 结论
1)采取双锥形子弹以相同速度撞击压杆,通过改变撞击端面的直径和双锥形子弹中间段直径,可以有效提高试件的加速度峰值。
2)改变双锥形子弹的弹长和尾段直径对试件加速度峰值的影响较低,相似外形的双锥形子弹改变弹长的最大增值比为7.7%,改变双锥形子弹尾端直径的最大增值比为2.12%。
3)改进的双锥形子弹在提升试件加速度峰值上有明显的效果,但是具体实验中子弹在气仓内需要增设子弹拖,这样能保持双锥形子弹在气仓内水平运动不发生偏移。
