航天器轨道仿真中的一种实时变轨仿真策略*
2019-11-13勾国斌闫月晖
吕 卓,张 旭,勾国斌,闫月晖
(1 北京理工大学, 北京 100081; 2 北京航天长征飞行器研究所, 北京 100076)
0 引言
轨道设计是航天器方案设计中的重要内容[1],包括轨道模型建立、制导率设计等。在轨道设计方案论证阶段,设计人员往往会面临大量的理论计算公式、符号和图表等,数据量庞大且抽象,导致理解困难,评审效率低。采用三维可视化仿真技术对航天器轨道进行仿真,可直观的展示航天器飞行和变轨效果,为设计工作带来便利;在此基础上实现实时变轨,即设计人员在仿真进程中根据航天器飞行情况适时发出变轨指令,控制航天器变轨飞行,便可在一次仿真中控制航天器完成多次变轨,观察航天器在轨道不同位置上的变轨效果,以及经多次变轨调整后航天器的轨道变化情况,进而验证设计方案可行性,降低试验成本,提高设计效率。
国内外学者对于航天器的三维可视化仿真进行了大量研究。文献[2]基于OpenGL设计了一种小卫星在轨运行可视化仿真系统,实现对小卫星的实时监测仿真;文献[3]利用Direct3D和3D MAX完成了探空火箭任务可视化仿真设计,帮助科研人员直观的了解探空火箭的飞行状况,并理解从探测任务或试验中获取的抽象数据;文献[4]开发了一种基于OpenGL的导弹飞行可视化仿真系统,能够实现导弹的实时飞行仿真,实时观测飞行仿真数据和弹体、舵面、喷管等部件的动态变化。此外还有航天器姿态跟踪控制[5]、导弹攻防视景仿真[6]和导弹攻击过程[7]等方面的仿真研究。上述研究借助不同的工具实现了航天器多种设计方案的三维可视化仿真,但对于航天器实时变轨仿真问题仍然考虑不足。对此,文中提出一种实时变轨仿真策略,重点研究通过合理配置弹道点计算与发送方式,在STK与MATLAB联合搭建的仿真系统中实现航天器实时变轨仿真。
1 轨道仿真原理
在导弹实际飞行任务中,为应对突发情况或调整导弹预期落点,设计人员会通过制导控制系统向导弹发送变轨指令,随后操纵机构作出主动调整,改变导弹受力状况,进而按照预期变轨。在模型计算层面即反映为制导变量的改变。因此,为实现导弹变轨仿真,首先要对某一特定的弹道模型选取制导变量,为其设置默认值,根据弹道模型进行弹道计算。在实施变轨时,通过程序控制接口向弹道计算引擎发送变轨指令,制导变量随即被更新,继而计算出新弹道数据。新弹道数据被发送至STK经处理生成新弹道曲线,导弹沿着新弹道曲线飞行,从而完成变轨。文中基于MATLAB与STK搭建实时变轨仿真环境,即通过MATLAB构建弹道计算引擎来计算和发送弹道数据,使用STK接收弹道数据并生成仿真动画。
导弹实时变轨仿真效果可归纳为两个基本要求,即实时性和对照性。实时性是指发出变轨指令后,窗口中的导弹能够根据控制系统特性和导弹气动特性等,按照规定的时间准确响应,生成新的弹道曲线并沿新的弹道飞行;对照性是指在变轨时,导弹飞行前方需保留一段变轨前提前生成的原有弹道曲线,与新生成的弹道曲线对照,以更好的观察到变轨效果。满足以上两个要求是实现实时变轨的难点和关键。
2 实时变轨仿真策略
2.1 定义
弹道点:根据弹道模型计算出来的一组数值解即为一个弹道点,STK接收弹道点后可生成弹道曲线,导弹沿弹道曲线飞行。弹道点(ballistic point, BP)具有以下形式:
BP={t,(x,y,z,vx,vy,vz)}
式中:t为弹道点对应的时刻;x、y、z为导弹在发射坐标系中的位置;vx、vy、vz为发射坐标系中沿x、y、z轴的速度。
实时对象:当导弹的仿真飞行速度无限接近于仿真窗口中弹道曲线生成速度时,则该导弹为实时对象。实时对象在视觉上会呈现在所过之处留下轨迹曲线的效果,如图1所示。其特点在于能够快速准确地响应变轨指令,生成新弹道曲线并沿该弹道继续飞行,原理在下文中详细叙述。
弹道辅助显示对象:为满足对照性,变轨时需在导弹飞行前方保留一段变轨前提前生成的弹道曲线,而这段曲线就需要弹道辅助显示对象来辅助生成。弹道辅助显示对象本质上是STK中的导弹对象,可通过设置使其模型不显示,只显示弹道曲线。弹道辅助显示对象作用下的仿真效果如图1所示,其作用原理在下文中详细叙述。
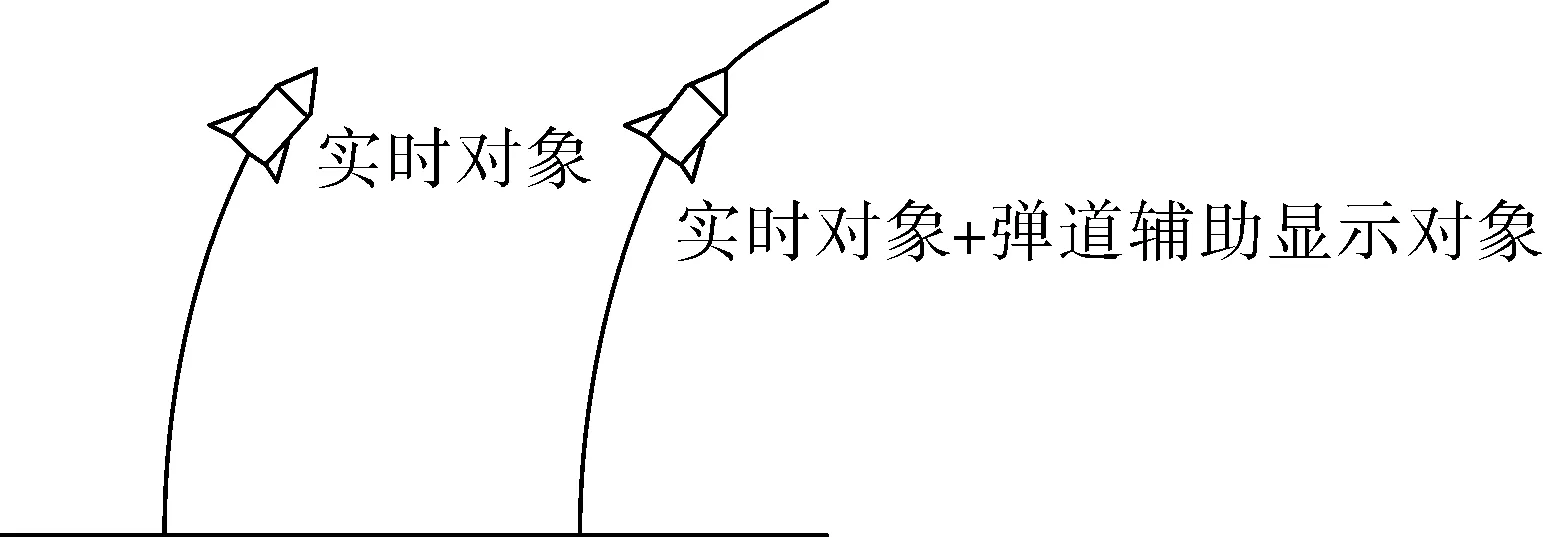
图1 实时对象与弹道辅助显示对象
主对象:将仿真显示的飞行中的导弹定义为主对象,主对象是仿真的主体。
2.2 实时性要求的分析与实现
导弹变轨实时性包括新弹道曲线立即生成与导弹立即沿新弹道曲线飞行两个方面,即可能存在着新弹道曲线已经生成而导弹仍沿着原有弹道曲线飞行的情况。
首先考虑变轨时新弹道曲线生成的实时性。仿真中弹道曲线生成需满足的基本条件是,所发送的弹道点对应时刻应提前于当前仿真时刻,即弹道曲线生成速度应快于导弹仿真飞行速度,这样下一点处的弹道曲线才会在导弹到达之前提前生成,确保仿真继续进行。在满足这一条件的基础上,考虑弹道点的计算与发送,共存在1次计算若干弹道点后逐个发送和计算出1个弹道点后随即发送两种方式。若采用第一种方式,则发布变轨指令时,上一轮计算所得若干弹道点可能仍处于发送阶段,新弹道点要等发送完毕后才开始计算,这在仿真中表现为变轨后所生成的弹道曲线依然是原有弹道曲线,一段时间后才生成新弹道曲线,造成变轨时新弹道曲线生成的滞后;若采用第二种方式,则发布变轨指令后将不存在多个弹道点逐个发送造成变轨滞后的问题,系统接下来计算出的弹道点即为新弹道点,新弹道点随即被发送至STK生成新弹道曲线,实现变轨,解决了新弹道曲线生成实时性的问题。
接下来考虑导弹飞行变轨的实时性。如果弹道点发送速度较快,则最新发送的弹道点对应时刻将大幅提前于当前仿真时刻,经系统处理提前显示的一段弹道曲线可能过长,发布变轨指令后虽然会立即生成新导弹曲线,但导弹仍沿提前显示的原有弹道曲线飞行,一段时间后才飞行至新弹道曲线,造成导弹飞行变轨的滞后;如果控制弹道点发送速度,使最新发送弹道点对应时刻尽可能小的提前于当前仿真时刻,则提前显示的弹道曲线会尽可能的短,此时导弹仿真飞行速度接近弹道曲线生成速度。一旦变轨,新弹道曲线会立即生成,导弹也会随即沿着新弹道曲线继续飞行,解决了导弹飞行变轨实时性的问题。
因此,为实现变轨实时性,在弹道点的计算与发送上应采用“计算即发送”的方式,同时控制弹道点计算速度,使所发送弹道点对应时刻尽可能小的提前于当前仿真时刻,此时的导弹即为实时对象。
2.3 对照性要求的分析与实现
导弹作为实时对象,在视觉上能够呈现如图1所示的效果。但根据对照性要求,需要在导弹飞行前方提前生成一段弹道曲线,以便在变轨时与新弹道曲线对照来观察变轨效果。这段提前生成的曲线就需要弹道辅助显示对象来帮助实现。仿真运行时,先计算出若干个弹道点,然后再开始发送,之后每发送一次则计算一次。新计算出来的弹道点发送至弹道辅助显示对象,而对于主对象,发送则从第一个弹道点开始。这样仿真中弹道辅助显示对象总比主对象提前若干弹道点显示,在仿真窗口中就可以呈现在主对象飞行前方提前显示一段弹道曲线的显示效果。弹道辅助显示对象比主对象提前的弹道点数越多,提前显示的弹道曲线就越长。变轨时,向主对象发送新弹道点的同时向弹道辅助显示对象发送其在变轨时刻对应的弹道点,使之停留在原地以保持原有弹道曲线显示,这样就可以在变轨后仍显示一段原有弹道曲线,以供对照。
2.4 一次变轨与多次变轨策略
2.4.1 一次变轨策略
基于以上分析提出一次变轨策略。仿真开始时新建主对象和弹道辅助显示对象,均作为实时对象。仿真窗口中主对象沿着弹道飞行,在弹道辅助显示对象的作用下其飞行前方提前显示一段弹道曲线。发布变轨指令后,主对象的新弹道曲线立即生成,主对象沿新弹道曲线飞行;与此同时,获取弹道辅助显示对象变轨时刻的弹道点,在每次发送数据时都将该弹道点发送至弹道辅助显示对象,保留一段变轨前的弹道曲线。变轨后主对象沿着新弹道飞行,可明显的观察出变轨效果。图2为上述策略的实现原理图。
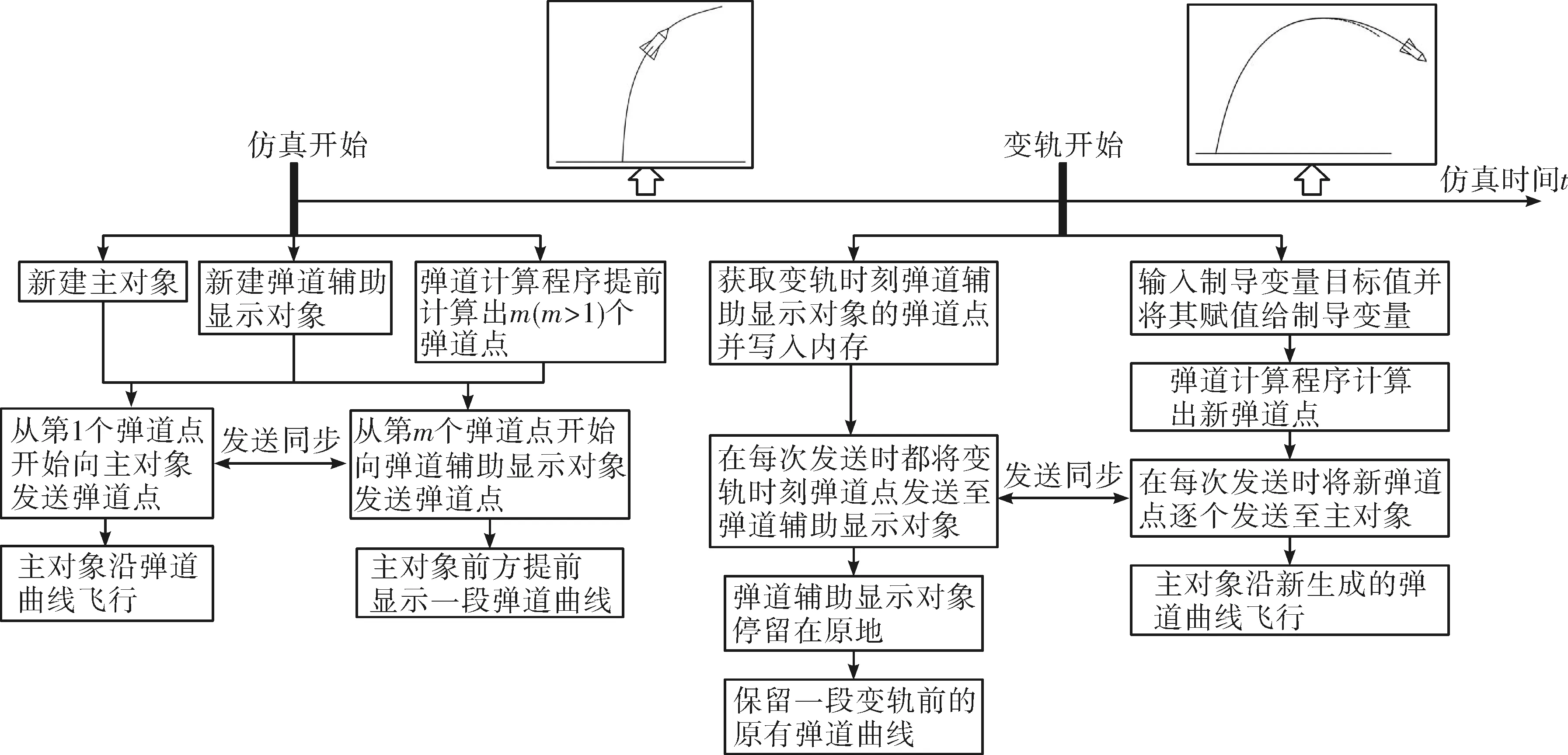
图2 一次变轨策略
2.4.2 多次变轨策略
在实现一次变轨仿真的基础上,需要实现对多次变轨的仿真。完成一次变轨后,原有的弹道辅助显示对象一直停留在原地,主对象没有了弹道辅助显示对象的配合,在飞行前方无法提前显示一段弹道曲线,若再次变轨,导弹会沿着新弹道曲线飞行,但无法保留一段原有的弹道曲线加以对照,进而无法满足仿真效果的对照性要求,这就需要新的弹道辅助显示对象来辅助显示。所以为实现多次变轨,在一次变轨时,除了原有的弹道辅助显示对象停留在原地以及主对象沿新弹道飞行以外,同时还要新建弹道辅助显示对象,并以变轨时刻主对象的弹道点为初值,经多次迭代计算出若干新弹道点,以覆盖原有的弹道辅助显示对象提前于主对象的若干个弹道点,之后再开始新一轮的发送和计算。继续读取下一个弹道点发送至主对象,将最新计算出来的弹道点发送至新建的弹道辅助显示对象,这样主对象就会沿着新弹道飞行,并且在前方提前生成了一段新弹道曲线,同时又保留了一段变轨前的弹道曲线。二次变轨、三次变轨等多次变轨均按照上述流程实现。图3即为上述策略的实现原理图。
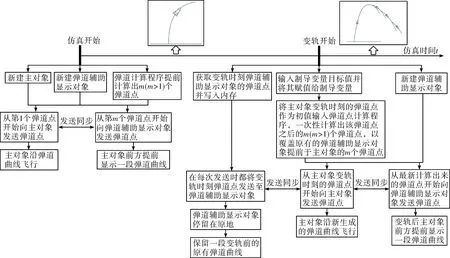
图3 多次变轨策略
3 实时变轨仿真试验
选取文献[8]中所述的标准弹道模型为弹道实例,同时选取攻角为制导变量构建导引操纵方程,基于STK与MATLAB搭建实时变轨仿真试验平台,以验证文中策略的可行性。仿真开始后,适时向导弹发送变轨指令,完成仿真试验。试验发现:
1)弹道计算引擎计算弹道点并发送至STK生成预期弹道曲线,如图4所示,主对象沿该弹道飞行,在飞行过程中顺利变轨,效果显著。

图4 试验弹道

图5 变轨过程
2)当导弹越过最高点开始滑翔时,输入目标攻角值发布变轨指令,导弹随即做出反应,生成新弹道曲线并沿着新弹道飞行,实时性较高。同时保留了一段原有的弹道曲线,原有弹道曲线和新弹道曲线同时存在,形成明显的对照,如图5所示。
3)仿真不仅完成了一次变轨,而且在飞行的不同时刻顺利完成了多次变轨。攻角从0°依次变为3°、6°、9°,导弹迅速做出变轨反应,射程与攻击地点均发生变化,效果如图5所示,图中标记点表示变轨地点。
4 结论
文中研究的实时变轨策略满足了实时性和对照性要求,在仿真过程中可根据需要实时变轨并获得明显的变轨效果,仿真结束后利用回放功能可进一步观察仿真细节,获得导弹射程、射高等弹道信息,并根据变轨情况评估制导率设计合理性,具有较高的有效性和可行性,为基于复杂模型的弹道设计方案的定量评估做了必要的技术准备。未来进一步研究将该策略应用于航天器三维可视化仿真平台,并在此基础上考虑变轨时航天器模型自身的位姿变换和机构的动态调整,构建功能更为完善的航天器飞行可视化仿真系统。
