《圆率考真图解》注记——曾纪鸿有没有计算出π的百位真值？

高红成

(天津师范大学数学科学学院，天津 300387)

《圆率考真图解》一卷是研究圆周率的专著，首版(1874)收入《白芙堂算学丛书》，卷首题“湘乡曾纪鸿(栗諴)、湘阴左潜(壬叟)、新化黄宗宪(玉屏)同述”[1]。1874年冬丁取忠(1810—1877)作序，称该书是“曾君栗諴所作也”，但又称：

曾君锐于思而勇于进，创立新法，以月余之力，推得圆率百位，并周求径率，亦以除法补至百位。而黄君玉屏又析圆率为半周、为象限、及度、分、秒、微、纤、忽、芒、尘，皆列为表，以备求八线之用。又与左君壬叟共为图解，使学者循序可知其立法之源。洵可谓难能而可贵矣。

曾纪鸿(1848—1881)的跋文(1874秋)称：

果臣先生嘱纪鸿等凝心构思，幸得创兹巧法，敛级甚速，按等推求，瞭如指掌。迩日深于算者，穷理之功多，演数之功少，反觉不切于日用。今左君壬叟、黄君玉屏竟用此术推得各弧背真数，至百位之多。庶几息诸家之聚讼，而为古之困于圆率者，置一左券也。

可见，该书中的主要方法和创见是曾纪鸿提出的，左潜和黄宗宪参与了计算和证明。该书的核心内容是，通过π/4(四十五度弧)的二分公式或五分公式结合反正切函数的幂级数展开式(格雷戈里级数)计算出π的100位真值(1)这里的“百位真值”指的是整数位和小数点后99位共100位与π的真值前100位数字均相同。。全书大致分为五部分。(一)写作缘起；(二)差角正切公式的几何证明；(三)计算π值的两种算法；(四)给出π/4，π，1/π等13个数值的100位真值，每个数值均为102位(包括整数位)，前100位是真值；(五)依据二分公式，给出π/4的15位真值算草示例；依据五分公式，给出π/4的24位真值算草示例。

曾氏所给圆周率的百位真值在19世纪70年代虽说不是最先进的成果，但已属难能可贵，在我国数学史上可谓是一个飞跃，之前最好的成果是1808年浙江秀水(现属嘉兴县)的朱鸿计算到40位，但25位之后与真值不合。后世史家，如李俨[2]、汤浅光朝[3]、李迪[4]对曾氏的成果给予了肯定。不过，书中示例有些错误，引发“曾纪鸿有没有算出π的百位真值”的疑问，给后学留下了继续探索的方向。本文发现《圆率考真图解》的一个新版本，对曾氏算法、数据的进行数理分析，结合一些佐证史料和前人的研究，试图消除疑问，对曾氏成果和计算予以肯定。

1 曾氏算法与圆周率简析

1.1 曾氏求圆周率的两种算法

按曾氏自述，他发现《代微积拾级》(1859)卷三第六款中“有大弧(α)正切、小弧(β)正切求较弧(α-β)正切”公式(即差角正切公式)

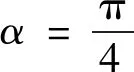
(1)

此式与反正切函数的幂级数展开式

(2)

结合就可以得到π/4的值，进而可求得π值。

曾氏在书中给出了这个正切公式的几何证明，并称式(1)为“自创”。他称式(2)为“徐君青术”，即徐有壬《测圆密率》卷二第六术，“君青”为徐氏的字。此式在欧洲称为格雷戈里级数，是英国数学家格雷戈里(James Gregory，1638—1675)1671年首先发现的。

紧接着，曾纪鸿认为，公式(1)(2)配合求π/4，因为2和3数值较小，计算时收敛速度较慢，他说“右草取数较旧术为简，惟前草以四为除法，遇首位为四以上之数，必除二次始降一位，犹嫌敛级略迟。”于是他“又推得一法，将四十五度弧背分作五分求之，敛级更速。”

他先运用差角正切公式得到π/4的五分公式

(3)

可以想见，在当时通过人工笔算，百位真值的计算量会更大，耗时会更长，曾纪鸿称三人“以月余之力”，才“推得圆率百位”。

1.2 曾氏所得到的圆周率百位真值

依据前文算法示例，曾氏“以百位为限”，求得“四十五度弧背(π/4)真数”为

依次乘以4，2，8后得到π(半周率)、π/2(象限弧)、2π(全周率)等3个数值，然后在这3个数值的基础上得到其它9个数值：π/18(十度弧)、十分弧、十秒弧、十微弧、十纤弧、十忽弧、十芒弧、十尘弧、1/π(圆径率)。最受关注的圆周率为

需要注意的是，这13个数值虽“以百位为限”，实有102位，“百位”指的是前100位为真值，最后两位尾数原文用双行夹注字号小写区别出来，意为误差数字，我们姑且称它们为“存疑数字”。依据这个结果，曾氏指出朱鸿所求的40位π值第25位之后与真值不合。

2 钱老的校证与疑问

钱宝琮先生(1892—1974)很早就对中国传统数学中圆周率的计算进行了研究，1923年他在《中国算书中之周率研究》一文中对曾氏的成果予以肯定[5]。但1927年钱老在南京拜访前辈崔朝庆(1860—1943)时曾得崔氏的提醒，“曾氏推算周率，其二十四位细草已有疏桀，决不能准至百位”，开始对曾纪鸿是否计算出百位真值有了怀疑[6]。1939年钱老经过仔细校对，发现《圆率考真图解》白芙堂本中π/4的24位真值细草有4处错误([6]，页335)：

1964年，钱老主编《中国数学史》时引用前面的论述，并且比较两种方法的计算量，指出法二不比法一高明，“π/4的二十四位数字是偶合”，“曾纪鸿有没有算出π的一百位有效数字是可以怀疑的”[8]。钱老治学严谨、质疑谨慎可见一斑，校正了曾氏算草的错误，同时也为后学留下继续探讨的问题。

1982年，杨中和《π的历史》一文注意到钱老的疑问，惜“至今未见新的辩解文章”[7]。

1988年，许康先生在一篇纪念曾氏的文章中对钱老的疑问进行了回应，他认为“曾纪鸿这项成果的价值主要在于得到了新的公式(3)，而不在于是否实施了计算”，并猜测“书中几处字误，很可能是抄写或者刻书时产生的”[9]。但这些不能解决钱老的疑问。实际上，曾氏是否实施了计算是这个疑问的关键。

3 几个发现

3.1 《圆率考真图解》的一个新版本

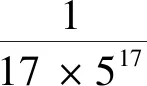
实际上，π/4的24位真值细草还有一处错误(v)，就是最后五个数值和(π/4)应为0.78539 81633 97448 30961 56604，而不是两个版本中的0.78539 81633 97448 30961 56600，但这个错误不影响最后得到π的24位真值误(尾数04或00乘以4后不涉及进位)，所以24位真值得以“偶合”。

由此可见，白芙堂本中π/4的24位真值细草确有错误，不过，与曾氏同时代的人能发现并校算出这些的错误，白芙堂本的失误很有可能是校对或者刊刻时造成的。

3.2 π/4、π/2、π、2π等四个数值的存疑数字以及算法分析

从1.1节对π/4的24位真值细草分析来看，曾氏实际上是把级数各项计算到小数点后25位，然后求和取前24位为π/4的真值，最后两个数字作为“存疑数字”。15位真值细草情况类似，只不过取最后一位为存疑数字。π/4的计算很重要，是计算其它数值的基础数据。

书中虽没有给出π/4的百位真值的细草，但我们注意到，曾氏给出102位的π/4、π/2、π、2π等4个数值的最后两位存疑数字，依次是“99”“98”“97”“94”(如表1)。验算可知，99依次乘以2，4，8后，不能同时得到后面三个两位存疑数字。曾氏所给的数据存在“玄机”，应该是经过优化的。

表1 曾氏所给π/4、π/2、π、2π等4个数值的尾数

一般来说，要保证一定的精度，将展开式(2)中各项计算到小数点后若干位，将最后几位尾数作为存疑数字，其余数字作为真值的做法是一个经验算法。对于π/4的真值而言，式(1)是两个数值和，留取最后一位作为存疑数字；式(3)是五个数值的和，留取最后两位尾数作为存疑数字。但要乘以4后求π的真值，两种方法则需留取最后3位尾数作为存疑数字。因此要得到π的百位真值，需将π/4最少计算到小数点后102位(共103位)。

进一步分析可知，π/4最后的存疑尾数需是三位，而且只有是990—999十个数中的“993”时，依次乘以2，4，8后，末尾三位数依次是986，976，944，舍去最后一位，才能与所给π/2、π、2π的末尾两位存疑数字同时相符。

表2 两种算法所得π/4的尾数

3.3 曾氏所给π值实际上有101位真值

经过比对，曾氏给出的102位π值(见1.2节)实际上前101位与真值相符，以前的研究都未曾注意到这一点。因为计算方法和误差估计，他们自己认为只是得到“百位真值”。如果有更好的结果作为参考，他可以说得到“101位真值”。

3.4 黄宗宪的记载佐证

1876年黄宗宪随郭嵩焘出使欧洲，1877年在伦敦一家博物馆发现一本数学书上记载了π的158位真值，他说

于博物馆天算书中觅得圆率真数一百五十八位，即翻行篋，检昔日与曾、左两君所推得百位者校之，一一吻合，何快如之!不但能证旧刻无布算之讹，且从此确知圆率真数已成铁案矣。谨录一纸寄归中华，想果师(指丁取忠)与栗兄(指曾纪鸿)见之当亦欣喜。(4)此条史料李俨先生最先发现([2]，页290)。汤浅光朝《解说科学文化史年表》“中国近代科学史”录有“1877年，左潜和曾纪鸿把圆周率计算到100位”([3]，页238)。“1877年”应该是黄宗宪的记载年代，记为《圆率考真图解》首版年“1874年”更为确切。[11]

这条史料可以作为曾氏计算出百位圆周率真值的一个佐证。

4 结语

综上，我们认为曾纪鸿的确是计算出圆周率的百位真值，他在文中所给的值是由其发现的π/4五分公式(3)结合反正切函数的幂级数展开式计算得到。5个级数各项均计算到小数点后102位，求和得到π/4的103位数值(包括整数位)，依次乘以2，4，8之后得到π/2、π、2π的数值，取前100位作为各量的真值，最后一位舍去，剩余2位数作为存疑数字，双行夹注字号书写区别。曾氏所给π值实际上有101位真值，式(3)是一个梅钦类公式。

致 谢感谢王彩华副教授、赵志学博士、硕士研究生张静同学等几位同事帮助分析数据。