射流动力学边界条件的研究*

曹建明，王德超，舒 力，张凯妹

（长安大学 汽车学院，西安 710064）

0 前 言

线性稳定性理论仅研究第一级波，因此仅应用第一级波的动力学边界条件[1]。但线性稳定性理论能够研究三维扰动的瑞利-泰勒波，因此本文将推导出三维扰动的第一级瑞利波和瑞利-泰勒波的线性动力学边界条件。非线性稳定性理论能够研究三级波，因此要应用第一级波、第二级波和第三级波的动力学边界条件[2]。但非线性稳定性理论仅研究一维扰动的瑞利波，因此本文将推导出一维扰动三级瑞利波的非线性动力学边界条件。

目前，对于线性稳定性理论，平面液膜、圆射流和环状液膜二维扰动的第一级瑞利波的动力学边界条件以及平面液膜二维扰动的第一级瑞利-泰勒波的动力学边界条件已有定论[3-18]。对于非线性稳定性理论，平面液膜一维扰动三级瑞利波的动力学边界条件和圆射流在特殊条件下（如：喷嘴出口液体流速为零，韦伯数等于 1）一维扰动三级瑞利波的动力学边界条件已有研究[19-20]。上述研究鲜有对于详细推导过程的论述。本文的推导结果与上述研究结果完全一致，创新点在于：从动力学边界条件的普适性原始表达式入手，经过细致全面的推导，将得到平面液膜、圆射流和环状液膜三维扰动瑞利波的线性动力学边界条件，以及平面液膜、圆射流和环状液膜三维扰动瑞利-泰勒波的线性动力学边界条件，得到圆射流和环状液膜一维扰动三级瑞利波的非线性动力学边界条件。给出各种动力学边界条件的简化和适用情况，并将全部的动力学边界条件全面、系统地相互关联在一起，为进行射流碎裂过程研究的学者提供各种物理模型下明确的动力学边界条件表达式。

动力学边界条件的通式由杨-拉普拉斯方程确定[3]。

1 液相与气相的应力张量差

1.1 平面液膜的应力张量差

对于沿x、y、z方向的三维扰动，有量纲形式的液相与气相的应力张量差为：

式中：p为扰动压力，Pa；μ为动力学粘度系数，Pa⋅s；u、v、w为沿x、y、z方向的扰动速度，m/s；为直角坐标系的哈密顿算子，其中，分别为沿x、y、z方向的单位矢量。角标“l”表示液相，“g”表示气相；“j= 1”表示平面液膜的上气液交界面，“j= 2”表示下气液交界面。

由于平面液膜很薄，三维扰动可以简化为一维扰动。一维扰动的线性稳定性理论应力张量差为方程（7）。由于液相有粘性，因此线性稳定性理论的液相压力pl和气相压力pgj要通过连续性方程和纳维-斯托克斯方程组（Navier-Stokes equations）求得。对于非线性稳定性理论，由于假设液相和气相均为无粘性、不可压缩的一维扰动理想流体，因此，方程（7）可以简化为：

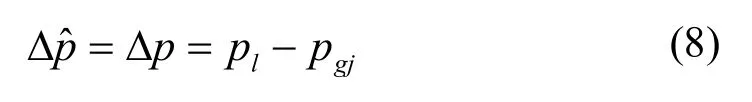
非线性稳定性理论的液相压力pl和气相压力pgj可以通过伯努利方程直接求得。

1.2 圆射流和环状液膜的应力张量差

对于沿r、θ、z方向的三维扰动，有量纲形式的液相与气相的应力张量差为：

对于圆射流和环状液膜，三维扰动也可以简化为一维扰动。一维扰动线性稳定性理论的应力张量差为方程（12）。圆射流和环状液膜一维扰动非线性稳定性理论的应力张量差与平面液膜的同式，为方程（8）。

2 由表面张力引起的附加压强

2.1 附加压强

如图1所示，曲率半径R1和R2分别表示平面液膜气液交界曲面上沿x方向和y方向的曲率半径，或者分别表示圆射流和环状液膜气液交界曲面上沿z方向和r方向的曲率半径。曲面DEFG为气液交界面，过O点做曲面DEFG的法线N，沿法线N做两个相互垂直的平面A1B1C1和A2B2C2，两平面与曲面DEFG相交于两条相互垂直的曲线A1B1和A2B2，曲线A1B1和A2B2的曲率半径分别为R1=OC1和R2=OC2。R3表示圆射流和环状液膜气液交界曲面DEFG沿z轴扭转一个角度θ后，到达曲面D'E'F'G'位置的曲率半径，R3=O'C2（O'与B2在图中重合），如图2所示。

如图3所示，当曲率中心在液体内部时，气体扰动压力要大于液体扰动压力，将气液交界面压向液体一侧弯曲，那么方程（1）中等号右侧应为负号，即由表面张力引起的附加压强为负；而当曲率中心在液体外部时，液体扰动压力要大于气体扰动压力，将气液交界面压向气体一侧弯曲，方程（1）中等号右侧应为正号，由表面张力引起的附加压强为正[4]。因此，如果沿某一方向的气液交界面有波动，那么附加压强为正负号。如果沿某一方向的气液交界面没有波动，而是一条直线，则附加压强为零；如果沿某一方向的气液交界面没有波动，而是一个圆，那么附加压强恒为负。

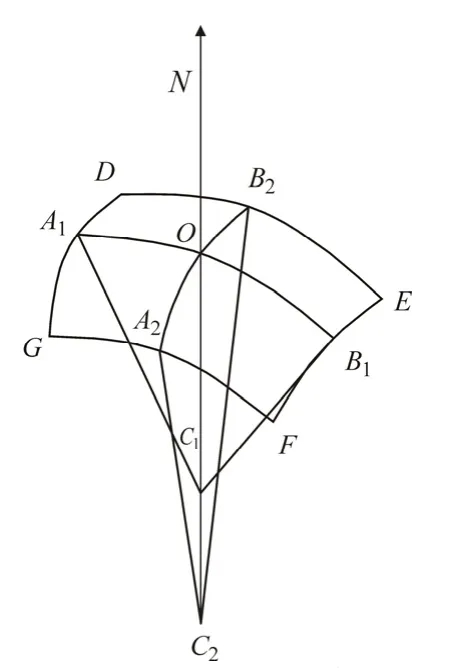
图1 平面液膜气液交界曲面上的曲率半径Fig.1 Curvature radius of liquid and gas interfaces of a plane liquid film

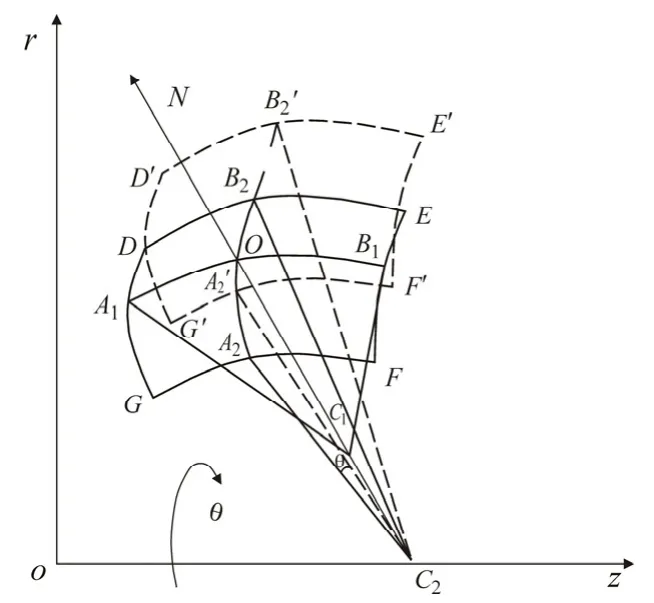
图2 圆射流和环状液膜气液交界曲面上的曲率半径Fig.2 Curvature radius of liquid and gas interfaces of a liquid jet and an annular liquid film

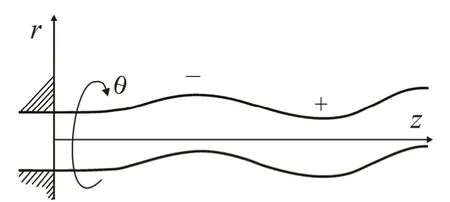
图 3 表面波气液交界面上由表面张力引起的附加压强正负号的选取Fig.3 Plus and minus of addition pressure caused by surface tension of liquid and gas interfaces of the surface wave

2.2 曲率半径和曲率

2.2.1 瑞利波

瑞利波是沿液体喷射方向的单向波，曲率半径和曲率指的是气液交界面表面波沿射流喷射方向曲线的曲率半径和曲率。对于直角坐标系的平面液膜，沿x方向曲面上任意一点的y方向气液交界线为一条直线，即沿y方向没有波动。因此，瑞利波的曲率半径和曲率仅与x坐标有关，而与y坐标无关。对于圆柱坐标系的圆射流和环状液膜，沿z方向曲面上任意一点的θ方向气液交界线为一个圆，即沿θ方向没有波动。但是，z方向曲线的曲率半径和曲率要受到r方向和θ方向曲率半径和曲率的影响。

（1）平面液膜瑞利波的曲率半径和曲率

如图1所示，平行于x轴的平面A1B1C1的曲率半径即为沿x方向的曲率半径R1=OC1。曲率为：

式中：角标“R”表示瑞利波，后文角标“T”表示泰勒波，角标“R-T”表示瑞利-泰勒联合波。Δα为弧线MM1上两端点M和M1切线的夹角，当M→M1时，Δα →dα，见图4a。Δs为弧线MM1的长度，当M→M1时，Δs →ds，见图4b。

式中：ξ为射流气液交界面表面波的扰动振幅，m。

由于表面波既有波峰又有波谷，是波动的。因此KR1有正负号。

式中：j= 1, 2。其中：（- 1）j中的“j= 1”表示波峰位置，“j= 2”表示波谷位置。ξj,xx中的“j= 1”表示平面液膜的上气液交界面，“j= 2”表示下气液交界面。

如图1所示，平行于y轴的平面A2B2C2的曲率半径即为沿y方向的曲率半径R2=OC2。当仅有瑞利波，而无泰勒波时，沿x方向曲面上任意一点的y方向气液交界线均为一条直线。由于直线的曲率半径R2= ∞，曲率则平面液膜非线性的瑞利波曲率为：

该式即为一条波动曲线的曲率方程。

忽略非线性的ξ的一阶偏导数项，对方程（20）线性化，得平面液膜线性化的瑞利波曲率。

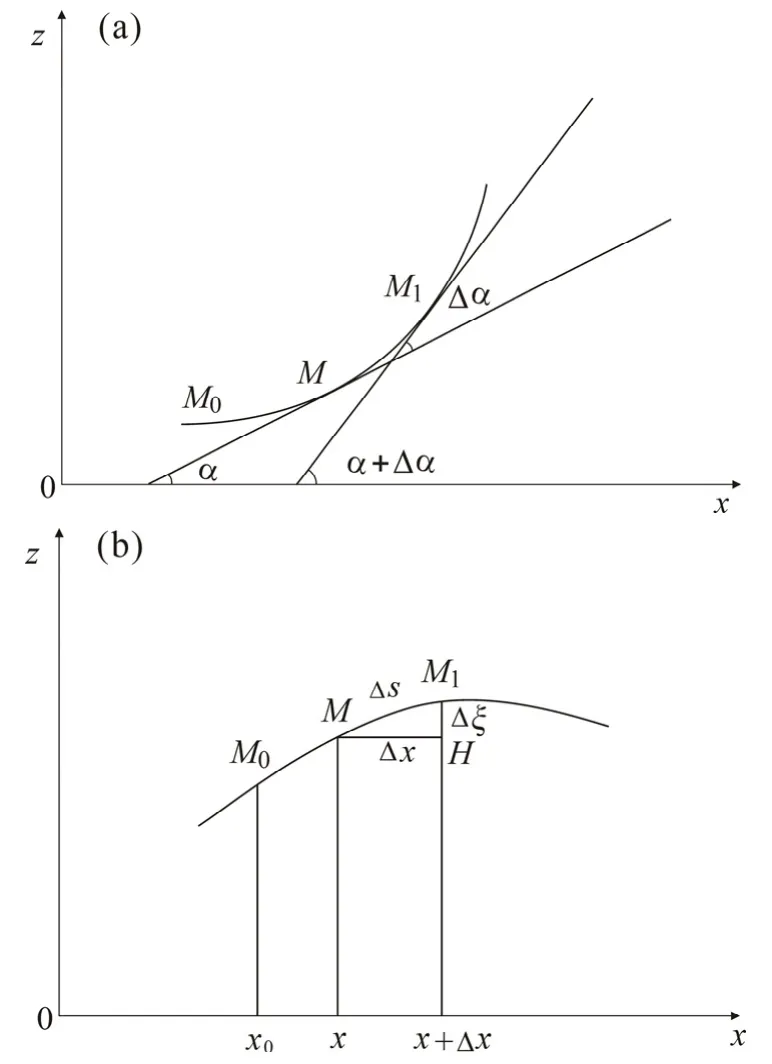
图4 平面液膜沿x方向的曲率半径Fig.4 x direction curvature radius of a plane liquid film

（2）圆射流和环状液膜瑞利波的曲率半径和曲率

如图2所示，R1、R2和R3分别表示圆射流和环状液膜沿z方向、r方向和θ方向的曲率半径。沿z方向平面A1B1C1的曲率半径为R1=OC1。由于A1B1为一条波动的曲线，因此有正负号。

如图2和图 5所示。沿平行于r方向的平面A2B2C2的曲率半径为R2=OC2。将弧线A2B2的曲率中心C2置于z轴底平面上，过O点做垂直于z轴、平行于r轴的辅助直线OB。过O点做辅助直角三角形ΔOMD、OC2⊥OM、ND⊥OB，则∠OMD=∠BOC2，三角形 ΔOMD与 ΔBOC2为相似三角形。当Δz→0时用于非线性稳定性分析；当此可以近似看作是小扰动，可用于线性稳定性分析。

图5 圆射流和环状液膜瑞利波的曲率半径R2Fig.5 R wave curvature radius R2 of a liquid jet and an annular liquid film

当仅有瑞利波，而无泰勒波时，围绕z轴是个圆面，则其附加压强恒为负号。由于瑞利波的波动，圆面的半径R2要随着z方向的位移而变化。因此，对于线性稳定性分析：

对于非线性稳定性分析：

如图2所示，当曲面DEFG绕z轴扭转一个角度θ后，扭转到曲面D'E'F'G'位置。由于表面张力的作用，曲面DEFG扭转到曲面D'E'F'G'后会有变形，O点除了会发生沿z轴的旋转之外，还会降低高度，即扰动振幅ξ变小，并沿z轴正向有一个微小位移。因此，曲率半径R3相对于R2会有所变化。因此，与旋转角度有关的曲率为：

与旋转角度有关的曲率KR3决定了圆射流的扭转。

瑞利波的曲率为方程（22）、（23）、（25）之和，即：

忽略掉非线性的ξ一阶导数项，对方程（26）进行线性化，得：

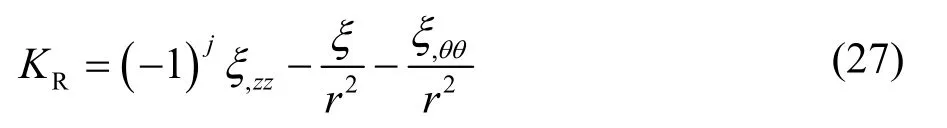
方程（27）即为线性稳定性分析瑞利波的曲率方程。

对于环状液膜，射流虽然也具有轴对称特点，但由于液膜很薄，一旦发生扭转，液膜会立即碎裂。因此，环状液膜不存在曲率半径R3和曲率KR3，在方程（27）中将曲率KR3项直接删去即可。即

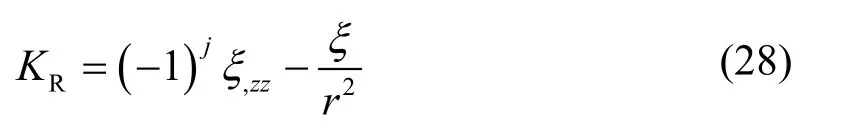
瑞利波非线性稳定性分析的曲率为方程（22）、（24）、（25）之和，即

对于非线性稳定性理论，由于圆射流仅研究常见的n= 0的正对称波形和n= 1的反对称波形，为单股状，并未发生扭转。环状液膜一旦发生扭转，液膜会立即碎裂。因此曲率KR3项应删去，方程（29）变成

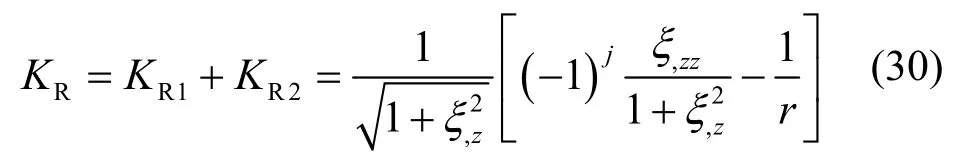
方程（30）即为圆射流和环状液膜非线性稳定性分析瑞利波正反对称波形的曲率方程。

2.2.2 瑞利-泰勒波

当既有瑞利波，又有泰勒波时，波动为沿射流喷射方向和垂直方向的双向波，曲率半径和曲率指的是气液交界面表面波曲面的曲率半径和曲率。对于直角坐标系的平面液膜，沿x方向曲面上任意一点的y方向气液交界线不再为一条直线，而是一条波动的曲线，即沿x方向和y方向均有波动。因此，瑞利-泰勒波的曲率半径和曲率与x坐标和y坐标均有关。对于圆柱坐标系的圆射流和环状液膜，沿z方向曲面上任意一点的θ方向气液交界线不再为一个圆，而是一条波动的曲线，即沿z方向和θ方向均有波动。

从数学的微分几何角度来说，过任意曲面上的某一点上具有无穷多个相互正交的平面，这些平面与曲面相交产生无穷多个相互正交的曲线，其中总会存在一条使得曲率K1成为极大值的曲线，与之正交的曲线的曲率K2为极小值。则K1和K2称为该曲面的主曲率。曲面上两个主曲率之和的平均值称为该曲面的平均曲率（又称为中曲率），即两个主曲率之积称为高斯曲率（又称为总曲率或全曲率），即K=K1K2[5]。该理论是由哥丁根大学的法国数学家Sophie Germain于1831年在她的著作《Theory of Elasticity》中最早提出的[6]。在流体力学中，采用平均曲率作为曲面曲率，并且将平均曲率中的2舍去。因此，流体力学中的曲面曲率为两个主曲率之和，即K=K1+K2[5-6]。

泰勒波的振幅非常小，其曲率半径趋近于无穷大，曲率则趋近于零。可以认为其曲率为极小值，与其垂直的瑞利波的曲率则为极大值。瑞利波曲线曲率与泰勒波曲线曲率之和就是瑞利-泰勒波曲面的曲率。因此，瑞利-泰勒波曲面的主曲率就是KR和KT。在对瑞利-泰勒波色散关系式的研究中发现，当忽略泰勒波时，瑞利波仍然存在，而当忽略瑞利波时，泰勒波将不复存在。说明瑞利波是主波，在射流的碎裂过程中起主导作用。

（1）平面液膜瑞利-泰勒波的曲率半径和曲率

沿x方向瑞利波的曲率KR见方程（20）。沿y方向泰勒波的曲率为：

则瑞利-泰勒波曲面的曲率为：

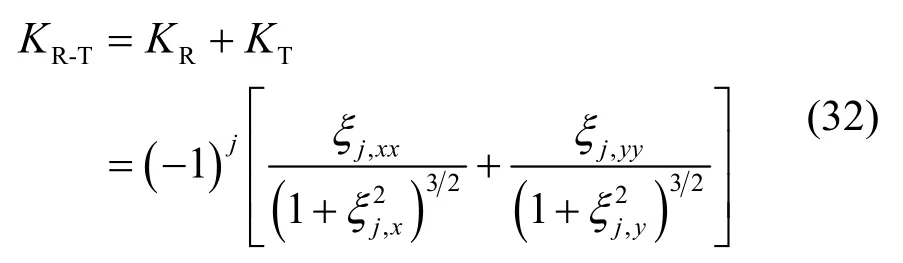
对方程（32）线性化，得平面液膜线性化的瑞利-泰勒波曲率。

（2）圆射流和环状液膜瑞利-泰勒波的曲率半径和曲率

围绕z轴不再是个圆面，而是一个波动的曲面，曲面不但沿θ方向有波动，而且其波动的半径还要随着z方向的位移而变化。θ方向、r方向和z方向的附加压强均有正负号。因此，圆射流瑞利波线性稳定性分析的曲率为方程（27）变成

环状液膜瑞利波线性稳定性分析的曲率为方程（28）变成

圆射流和环状液膜瑞利波非线性稳定性分析的曲率为方程（29）变成

对于圆射流的正反对称波形和环状液膜，非线性稳定性分析的曲率方程（30）变成

根据弧长与弧度的关系，ξ,s=ξ,(rθ)。对于旋转角度，r可以看作常数，有因此，沿θ方向泰勒波的曲率为

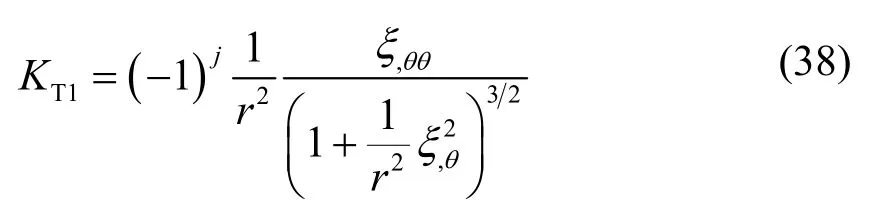
沿r方向泰勒波的曲率，对于线性稳定性分析

对于非线性稳定性分析

沿z方向泰勒波的曲率，对于线性稳定性分析

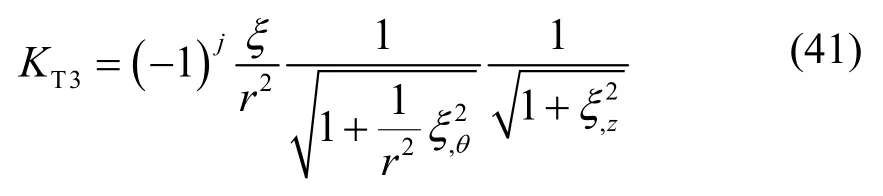
对于非线性稳定性分析

泰勒波线性稳定性分析的曲率为方程（38）、（39）、（41）之和，即

对方程（43）线性化，得

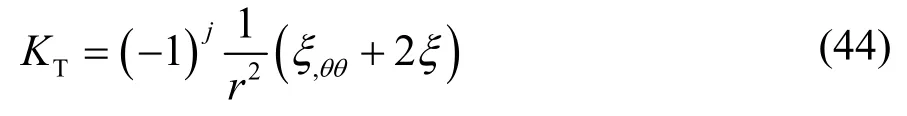
泰勒波非线性稳定性分析的曲率为方程（38）、（40）、（42）之和，即

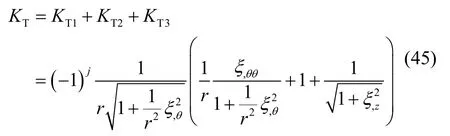
圆射流瑞利-泰勒波线性稳定性分析的曲率为方程（34）与（44）之和，即

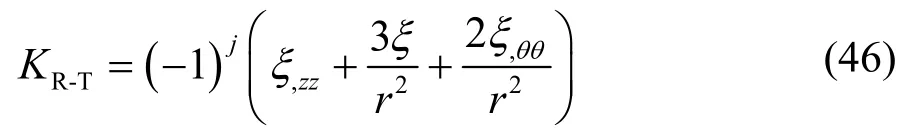
环状液膜瑞利-泰勒波线性稳定性分析的曲率为方程（35）与（44）之和，即

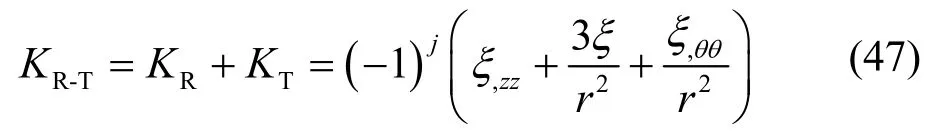
瑞利-泰勒波非线性稳定性分析的曲率为方程（36）与（45）之和。即

目前，由于非线性稳定性理论只研究到瑞利波，圆射流和环状液膜采用的曲线曲率方程均为（30），而由于用于研究瑞利-泰勒波的曲面曲率方程（48）太过复杂，目前尚未有人尝试使用。

3 平面液膜的动力学边界条件

射流的动力学边界条件为液相与气相的应力张量差等于由表面张力引起的附加压强。

3.1 平面液膜的线性动力学边界条件

线性稳定性理论能够研究粘性流体。粘性液体射流必须由连续性方程和纳维-斯托克斯方程组得到的扰动压力差确定动力学边界条件，为线性的动力学边界条件。平面液膜有量纲形式的线性三维扰动瑞利波动力学边界条件为

方程（49）～（51）两侧同除以液相基流压力、即液相喷射压力Pl，并将气液压力比液流韦伯数液流欧拉数液流雷诺数代入，得瑞利波量纲一化的动力学边界条件。

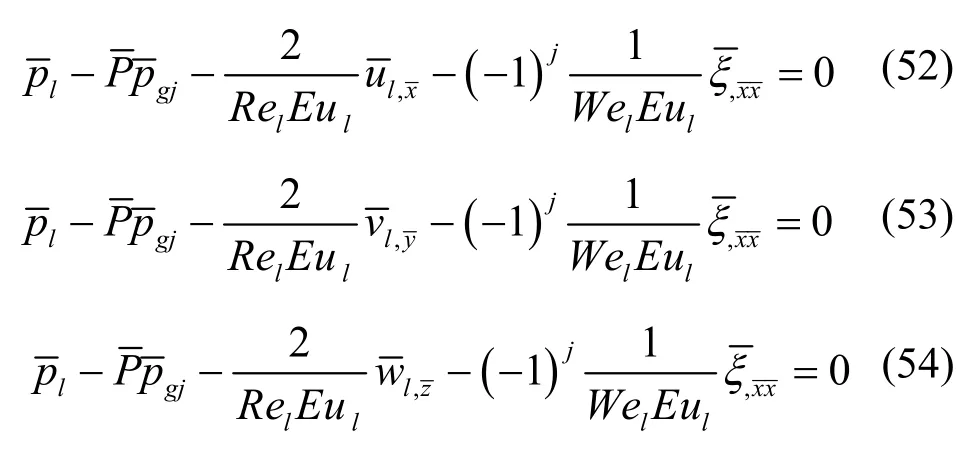
对于一维扰动，则取方程（51）和方程（54）即可[7-11]。

对于瑞利-泰勒波，有量纲形式的线性三维扰动瑞利波动力学边界条件为

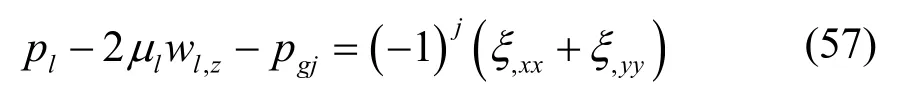
将方程（55）～（57）量纲一化，得瑞利-泰勒波量纲一化的动力学边界条件。

对于一维扰动，则取方程（57）和（60）即可。

对于无粘性流体，只需将方程（49）～（60）中含有μl和Rel的粘性项直接删去即可。

3.2 平面液膜的非线性动力学边界条件

目前，对于平面液膜的非线性稳定性理论，研究的是无粘性、不可压缩的理想流体。理想流体允许采用伯努利方程得到的压力差来确定动力学边界条件。对于理想流体射流的研究采用的是一维扰动的非线性稳定性理论。与运动学边界条件同样，非线性稳定性理论的扰动振幅有第一级波、第二级波和第三级波之分。目前的非线性稳定性理论仅研究正对称和反对称模式的瑞利波。

平面液膜的非线性动力学边界条件为

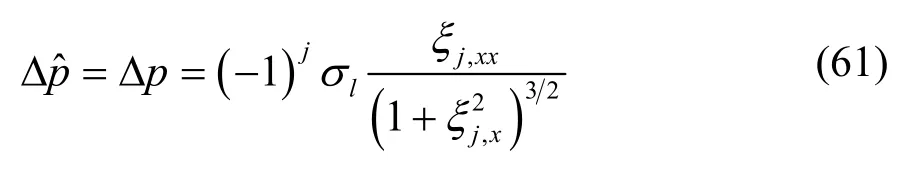
式中：Δp=pl-pgj（MPa）为液气相压力差。理想流体的动力学边界条件又可称为拉普拉斯方程。

以速度势函数ϕ表示的伯努利方程气液相一般形式为

式中：t为时间；速度势函数的定义为u=φ,x，w=φ,z。

对于多级表面波，有

式中：m= 1, 2, 3为表面波的级数为拉格朗日积分常数。对于液相，由于基流速度Vl=0，有对于气相，由于是静止气体环境，则f（t）=0gj。gz为体力势，也就是重力势。由于细小的喷雾液滴受重力影响很小，弗劳德数（Froude number）Fr很大，因此重力势可以忽略不计，即gz=0。方程（63）可以写为

将方程（64）和（65）代入方程（61），可得有量纲形式的平面液膜瑞利波动力学边界条件，适用于对理想流体的非线性分析[19]。

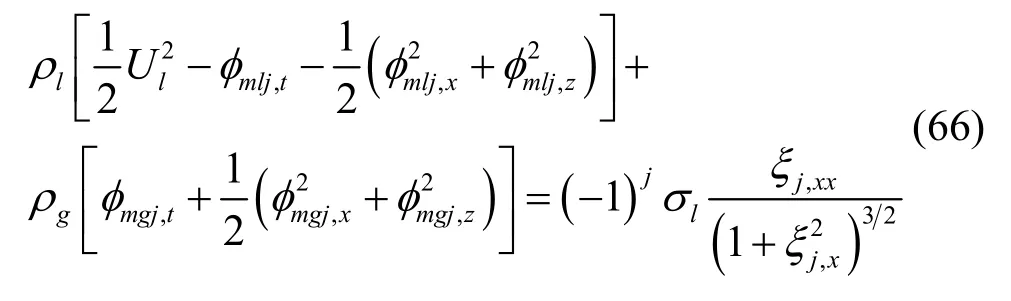
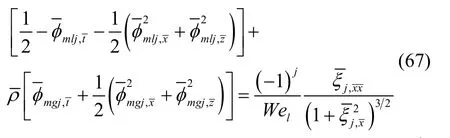
将方程（68）分别代入方程（66）和（67），可得平面液膜经麦克劳林级数展开的有量纲和量纲一化的多级波动力学边界条件。

和

平面液膜线性化边界和经麦克劳林级数展开的非线性动力学边界条件的边界选取位于：有量纲形式的液相 -a≤z≤a；气相a≤z≤∞（j= 1）和-∞≤z≤-a（j= 2）。量纲一形式的液相（j= 2）。其中：a为平面液膜在喷嘴出口处的半厚度。

4 圆射流的动力学边界条件

4.1 圆射流的线性动力学边界条件

圆射流有量纲形式的线性三维扰动瑞利波动力学边界条件为

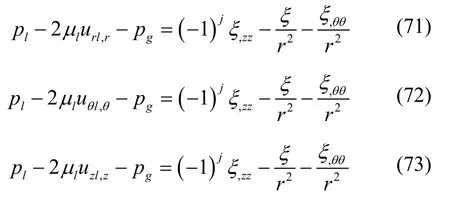
方程（71）～（73）两侧同除以Pl，得瑞利波量纲一化的动力学边界条件。

对于一维扰动，则取方程（71）和（74）即可[12-16]。

对于瑞利-泰勒波，有量纲和量纲一化的线性三维扰动瑞利波动力学边界条件为

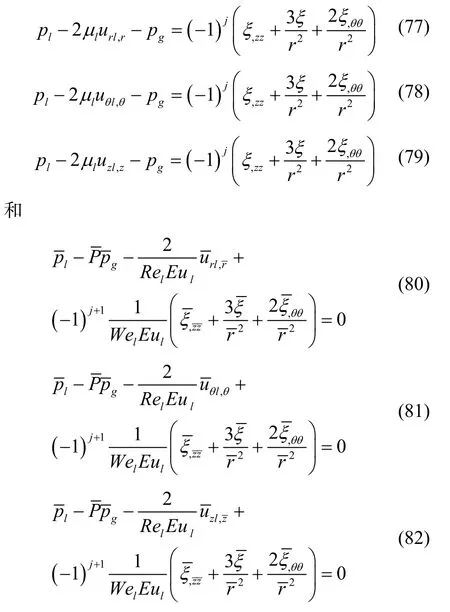
对于一维扰动，则取方程（77）和（80）即可。

对于无粘性流体，只需将方程（71）～（82）中含有lμ和Rel的粘性项直接删去即可。

4.2 圆射流的非线性动力学边界条件

圆射流一维扰动瑞利波正反对称波形（阶数n=0, 1）的非线性动力学边界条件为拉普拉斯方程。

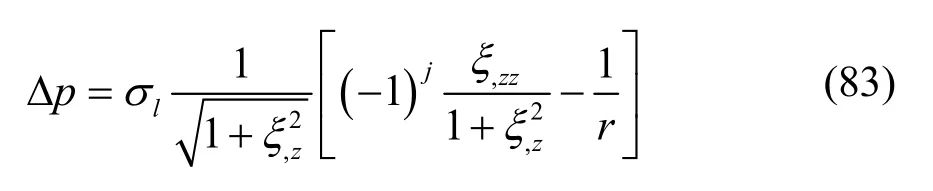
用势函数ϕ表示的伯努利方程气液相合式为

对于多级表面波，有

式中：m= 1, 2, 3为表面波的级数为拉格朗日积分常数。对于液相，由于基流速度Url=0，有对于气相，由于是静止气体环境，则fgj（t）=0。gz可以忽略不计。方程（85）可以写为

将方程（86）和（87）代入方程（83），且非线性位移r=a+ξ，可得圆射流有量纲形式的非线性动力学边界条件。

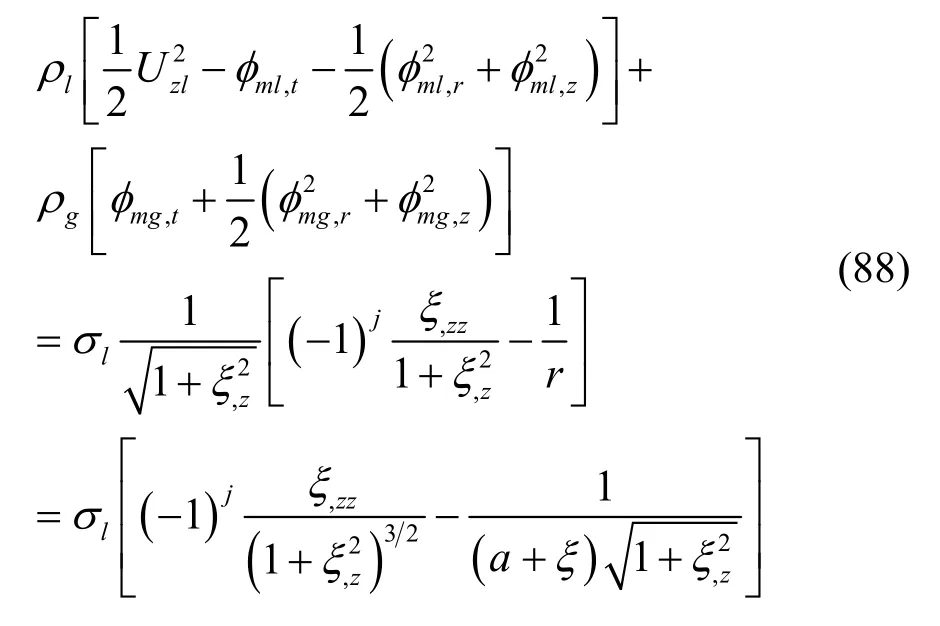
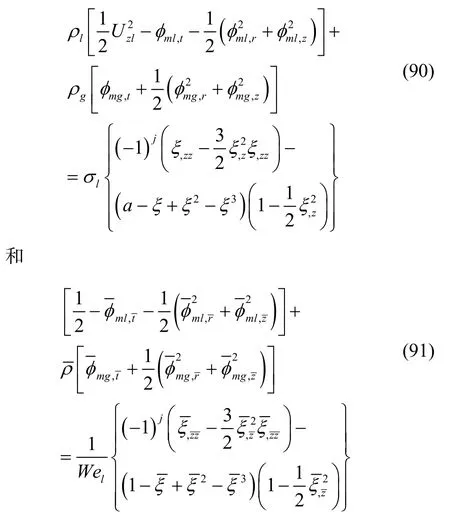
圆射流线性化边界和经麦克劳林级数展开的非线性边界选取位于：有量纲形式的液相0≤r≤a；气相a≤r≤∞。量纲一化的液相气相其中：a为圆射流在喷嘴出口处的半径。

5 环状液膜的动力学边界条件

5.1 环状液膜的线性动力学边界条件

环状液膜有量纲形式的线性三维扰动瑞利波动力学边界条件为

方程（92）～（94）两侧同除以Pl，得瑞利波量纲一化的动力学边界条件。

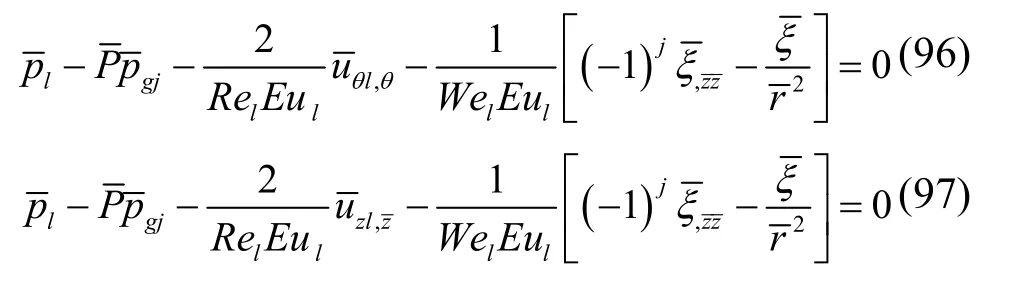
对于一维扰动，则取方程（92）和（95）即可[17-18]。

对于瑞利-泰勒波，有量纲和量纲一化的线性三维扰动动力学边界条件为

对于一维扰动，则取方程（98）和（101）即可。

对于无粘性流体，只需将方程（92）～（103）中含有μl和Rel的粘性项直接删去即可。

5.2 环状液膜的非线性动力学边界条件

环状液膜一维扰动瑞利波的非线性动力学边界条件为拉普拉斯方程，与方程（83）同式。

用势函数ϕ表示的伯努利方程气液相合式与方程（84）同式；多级表面波的与方程（85）同式。液相伯努利方程与方程（86）同式，气相方程为

将气液相伯努利方程（104）和（86）代入方程（83），且非线性位移r=rj+ξj，可得环状液膜有量纲形式的非线性动力学边界条件。

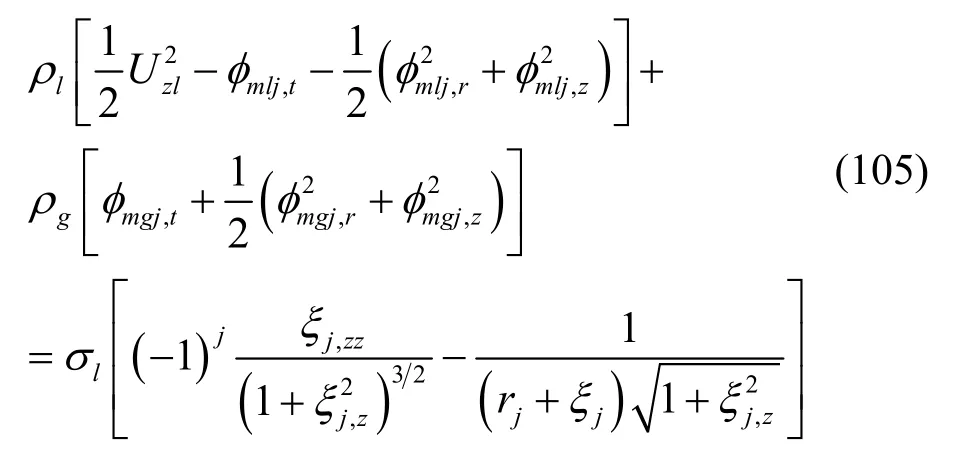
环状液膜量纲一化的非线性动力学边界条件为

环状液膜线性化边界和经麦克劳林级数展开的非线性边界选取位于：有量纲形式的液相ri≤r≤ro；气相 0≤r≤ri（j= i）和ro≤r≤ ∞（j= o）。量纲一形式的液相和其中：ri为环状液膜在喷嘴出口处的内环半径，ro为在喷嘴出口处的外环半径，

6 结 语

对于射流的线性和非线性动力学边界条件，学者们给出的各种表达式并不全面。本文从动力学边界条件的普适性原始表达式入手，对平面液膜、圆射流和环状液膜气液交界面三维扰动瑞利表面波、以及瑞利-泰勒表面波的线性动力学边界条件和一维扰动多级瑞利表面波的非线性动力学边界条件进行了全面、系统的详细推导，并给出射流的各种动力学边界条件的适用条件。为进行射流碎裂过程研究的学者提供了各种明确的动力学边界条件表达式。