天然气水合物沉积物分解过程中本构关系研究*

2019-11-05朱一铭陈忠勇周述扬

新能源进展 2019年5期

朱一铭，陈晨，陈忠勇，周述扬

（南京理工大学能源与动力工程学院，南京 210094）

0 引言

天然气水合物由于其储量大、分布广泛、清洁燃烧、便于运输等优点，在世界范围内得到了广泛关注，被认为是一种能够替代传统化石燃料的新型能源[1-3]。然而，天然气水合物是一种亚稳态化合物，受温度和压力的影响，即使温度和压力发生极细微的变化，天然气水合物都将会不可避免地发生分解[4-6]。水合物分解可能会破坏沉积物的骨架结构，这将大大降低沉积物的机械强度，导致水合物储藏地层发生变形，造成地质结构不稳定，结果必将增加开采过程中工程设施的安全隐患，甚至诱发滑坡等地质灾害[7]。因此，为了实现天然气水合物资源的安全高效开采，在对其进行商业化开发利用之前，对水合物及其沉积物的力学稳定性进行研究是十分必要的。

本构模型是描述材料在外部荷载作用下变形特性的基础，同时也是地层变形数值模拟分析的理论基础，对土木工程建设施工的设计和计算具有重要意义。MIYAZAKI等[8]在大量的三轴实验数据基础上，提出了适用于天然气水合物沉积物的变量-柔量本构模型，该模型可以较好地模拟天然气水合物沉积物的应力应变关系，从而预测水合物沉积物的强度及变形特性。李洋辉等[4]在剑桥模型的基础上，提出了一个新的弹塑性本构模型，通过模型预测的不同饱和度天然气水合物沉积物的应力-应变曲线与实验数据对比，发现该本构模型较好地模拟了实际天然气水合物沉积物的强度及变形特性，能够准确反映天然气水合物对沉积物强度、刚度和变形特性等的影响。孙翔等[9]在热力学准则及临界状态概念的基础上，提出了一种适用于天然气水合物沉积物的本构模型，与传统模型相比，该模型可以预测排水剪切三轴实验过程中的水合物沉积物应力软化现象，并且研究还发现水合物沉积物的体积蠕变是由于水合物饱和度变化引起的。

综上所述，目前对天然气水合物及其沉积物的本构模型研究已取得了一定进展，但是考虑水合物分解对其本构模型的影响往往被忽略[10-12]。本文以孔隙度40%的天然气水合物沉积物为研究对象，基于三轴压缩实验，研究获取天然气水合物沉积物在分解不同阶段及不同围压条件下的应力应变曲线，并基于邓肯-张（Duncan-Chang）本构模型，计算本构关系式中各实验参数与围压及分解时间的关系，最终构建适用于水合物分解过程中沉积物的本构模型，为预测天然气水合物储层的力学特性提供理论基础。

1 实验方法

1.1 样品制备

采用混合制样法制取沉积物试样[13-15]。首先，制备含冰的甲烷水合物，在-10℃环境温度下，采用标准60目筛获取粒径小于250 μm的冰颗粒，并取一定量的冰颗粒放入密封反应器中，将压力为10 MPa的甲烷气体注入高压反应釜，在48 h之内即可生成水合物。在每次生成水合物之后，随机取出部分放置在 -3℃冷库环境下（常压），保持足够长时间从而使水合物完全分解，计算这部分水合物分解前后的质量差，根据质量差计算出生成的甲烷水合物饱和度，本实验中甲烷水合物饱和度在26% ～ 33%之间。随后，将高岭土与冰粉水合物按照一定比例充分混合均匀（孔隙度40%），并放入制样装置中分层击实，最终获取高125 mm、直径61.8 mm的天然气水合物沉积物样品。高岭土来自于山东宁阳信通膨润土有限公司，粒径分布曲线如图1所示，其中值粒径为5.545 μm。根据试样体积，以及甲烷水合物、冰颗粒和高岭土的密度，计算出孔隙度为40%的沉积物试样所需各部分材料的质量，保证此圆柱形试样中含甲烷水合物冰粉与高岭土的体积比为4∶6，其中含甲烷水合物冰粉质量为147 g，高岭土质量为553 g。此外，有研究结果表明，高岭土颗粒物性分析及粒径分布结果与海洋土十分接近，并且基于这两种材料制取的水合物沉积物力学性质也非常相似，可用高岭土作为替代材料并进行力学特性研究[15]。

图1 高岭土颗粒粒径分布曲线Fig.1 Grain size distribution curve of kaolin clay

1.2 实验过程

实验仪器采用 DDW-600微机控制水合物三轴试验机，此装置的轴向系统包括了主机轴向加载框架和轴向控制器等，如图2所示[16]。

通过混合制样法，待天然气水合物沉积物样品制备完成之后，从制样模具中取出试样，修整试样表面直至光滑平整。随后，在样品的上下表面分别放置上下压块，用橡胶膜包裹成型样品，再将样品放入力学实验装置的压力室中，在预设围压和温度条件下进行固结。最后，在不同围压条件下，对天然气水合物沉积物试样开展一系列三轴压缩试验，获取其应力应变曲线，并对同围压条件下，在水合物分解各阶段的沉积物试样进行不排水排气三轴压缩实验，获取其力学实验参数。实验工况条件下如表1所示。

图2 实验装置系统图Fig.2 System diagram of the experimental device

表1 天然气水合物沉积物力学实验工况Table 1 Experimental conditions of the triaxial tests

2 结果与讨论

基于三轴压缩实验，研究获取了天然气水合物沉积物在分解不同阶段的应力应变曲线，以及破坏强度等力学参数，从而分析水合物分解过程中沉积物试样的强度变化，揭示沉积物试样强度的衰减规律，并基于力学实验参数及 Duncan-Chang本构模型，最终构建一个适用于天然气水合物沉积物分解过程的本构关系。

2.1 应力应变曲线

不同围压条件下，沉积物试样在天然气水合物分解前后的应力应变曲线如图3所示。由图可知，在一定的围压条件下，试样的偏向力先随着轴向应变的增大而增大，随后增加的幅度逐渐减弱，最终达到一个定值。水合物沉积物的应力应变曲线大致可以分为以下三个阶段[17]。

第一个阶段是准弹性阶段。在此阶段中，随着轴向应变的增大，偏应力的大小迅速增加，甚至可以看作是线性增大。在这个阶段中，水合物沉积物的变形是弹性变形，在卸载过程中应力和应变之间仍然保持线性关系，在卸载完全之后，变形可以完全恢复。

图3 不同围压下水合物分解过程中沉积物应力应变曲线（温度为 -5℃，应变速率为1 %/min）Fig.3 Stress-strain curves of the sediments during the hydrate dissociation under different confining pressures

第二个阶段是屈服阶段。准弹性阶段的最大值被称为弹性极限，所对应的偏应力被称为起始屈服强度[18]。当轴向应变超过起始屈服强度对应的应变值时，偏应力随着轴向应变的增大而不断增大，但是与第一阶段相比，偏应力的增长程度呈现明显放缓的趋势。也就是说，在其他条件相同的情况下，如果要增大相同大小的应变，所需要加载的应力会逐渐变小。在这个阶段，试样的变形除了弹性变形外，还存在着明显的塑性变形。在卸载之后，水合物沉积物试样并不能完全恢复，而是只有其中弹性形变部分可以恢复。

第三个阶段是强化阶段。在这个阶段，随着轴向应变的不断增长，偏应力的增长变得十分缓慢。也就是说，只需一个很小的偏应力增量，就会产生很大的变形。此时，水合物沉积物试样抵抗变形的能力十分微弱，沉积物试样可以看作已经被破坏了。

图4给出了不含水合物时，高岭土冰粉混合物的应力应变曲线，高岭土冰粉混合物的应力应变曲线呈现较弱的软化趋势，并且在围压越大的条件下，软化趋势越明显。此外，对比图3中不分解时高岭土水合物沉积物的应力应变曲线，发现水合物的存在会对高岭土沉积物试样的剪切强度起到增强作用，这可能是由于水合物颗粒和土颗粒之间产生的胶结作用增强了试样的结构，从而导致强度增加。

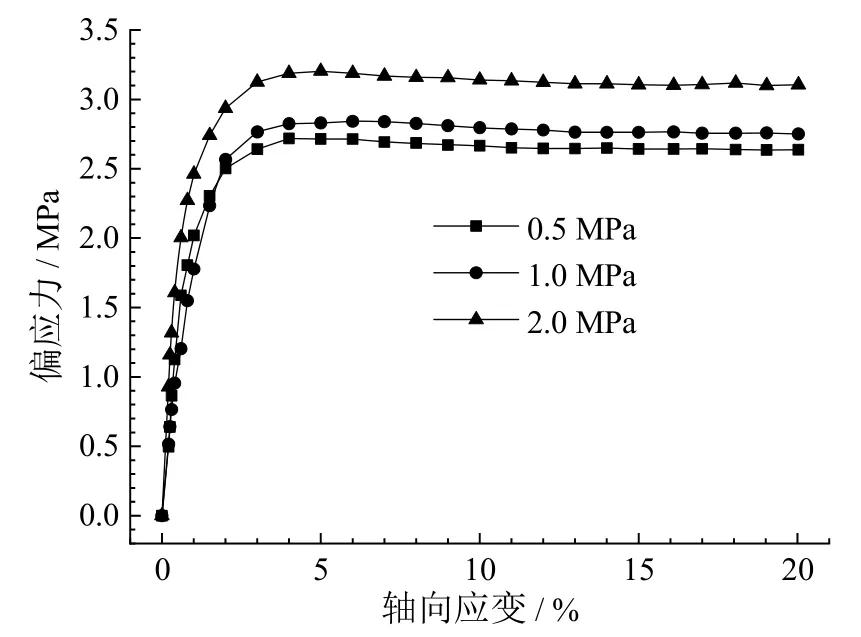
图4 不同围压下高岭土冰粉混合物应力应变曲线（温度为-5℃，应变速率为1 %/min）Fig.4 Stress-strain curves of ice-clay mixtures under different confining pressures

2.2 破坏强度与分解时间的关系

取沉积物试样发生15%轴向应变时所对应的偏应力值作为试样的破坏强度，图5显示了不同围压条件下，天然气水合物沉积物试样的破坏强度随分解时间的变化曲线。

图5 不同围压下破坏强度与分解时间的关系Fig.5 Relationship between failure strength and dissociation time under different confining pressures

从图5可看出，沉积物试样的破坏强度随水合物分解过程的进行而逐渐减小，且其减小的速率呈现出衰减的趋势；相同分解时间条件下，围压越高，沉积物试样的破坏强度越大[16]。由于水合物的分解，水合物颗粒自身强度下降，颗粒之间胶结作用减弱，从而造成了试样结构松弛。并且水合物分解过程中，产生的自由气、水聚集在孔隙中，试样内部孔隙压力增加，从而造成了有效围压的降低，而有效围压是影响水合物沉积物剪切强度的一个重要因素[4]，有效围压越低，水合物沉积物试样强度越小。此外，在低温条件下，分解产生的自由水造成试样内部冰颗粒增多，且冰颗粒可能出现连块的情况，冰的连块类似于水合物的胶结，从而导致试样破坏强度增大，最终造成了试样强度下降的速率逐渐减弱的现象。另一种可能的原因是由于甲烷水合物在分解过程中具有独特的“自保效应”[19]，较厚的冰层覆盖在水合物表面使得分解速率变慢，进而使强度衰减速率下降。三种围压条件下，沉积物试样的破坏强度变化曲线趋势基本保持一致，破坏强度与分解时间的关系式可用二项式关系表述：

式中：t表示天然气水合物沉积物的分解时间，A0、A1、A2是与围压有关的参数，通过数据拟合的方法，获取如下关系式：

在已知实验围压与天然气水合物分解时间的条件下，通过确定三个拟合参数A0、A1、A2的值，即可计算出此时沉积物试样的破坏强度值。

2.3 本构关系研究

基于三轴压缩实验结果，获取了天然气水合物沉积物试样的应力应变关系，为了从理论上进一步分析天然气水合物在分解前后的力学特性，基于Duncan-Chang模型，对沉积物试样的力学特性作进一步的分析。

土力学研究中 Duncan-Chang模型被广泛应用于分析硬化型应力应变曲线，而本实验所获取的沉积物试样的应力应变关系符合这一特征，因此在借鉴Duncan-Chang模型的基础上，通过引入围压与分解时间这两个变量，构建了水合物分解过程中沉积物试样的本构关系。Duncan-Chang本构关系可以表述为：应变和偏应力的比值与应变成线性关系，其公式为[18]：

图6给出了Duncan-Chang非线性模型中纵坐标ε1/(σ1-σ3)与横坐标ε1之间的变化关系，不难发现，在不同围压条件下，两者之间都满足较好的线性关系，其线性相关系数均大于 0.99，完全满足构建Duncan-Chang本构关系的要求。

根据实验数据，已知各个应变时所对应的偏应力值，则可以求出不同围压条件、不同分解时间阶段下，每一个应变时所对应的本构模型参数a、b的值，如表2所示。

图6 不同围压下 ε1/(σ1 -σ3)与ε1之间的变化关系曲线Fig.6 Relationship between ε1/(σ1 -σ3) and ε1 under different confining pressures

表2 天然气水合物不同分解阶段条件下沉积物本构关系中参数a、b值Table 2 The parameters a and b of this constitutive model of hydrate-bearing sediments during hydrate dissociation

2.3.1 参数a与分解时间的关系

由表2可以看出，在围压为0.5 MPa和1 MPa条件下，实验参数a的值随天然气水合物分解过程的进行逐渐增大，且大致呈线性增加的趋势。而在围压为2 MPa条件下的a值波动很小。因此，采用线性关系来统一描述三种围压条件下的实验参数a值的变化关系。

基于线性关系拟合数据，研究获取了参数a与分解时间的关系：

式中：t表示天然气水合物沉积物的分解时间；B0、B1是与围压有关的参数。数据拟合发现，两者之间呈现二项式关系：

因此，只要给出力学实验中围压的条件，即可计算出上述参数B0、B1的值，再根据相应的天然气水合物分解时间t值，即可求出该本构关系中实验参数a的值。

2.3.2 参数b与分解时间的关系

参数b的值的计算方法和参数a不同，对式（5）求极限，可以得出：

本文研究中为了简化模型，便于计算，引入了一个新的参数：破坏比Rf，定义为破坏强度与极限偏应力的比值，用公式表示为：

因此，根据式（9）和式（10），破坏强度就可以表示成破坏比与极限偏应力的乘积：

基于以上分析，可知b值和破坏强度、破坏比有关，因此只要确定破坏比的值，再根据式（1）～式（4）求出某一围压、天然气水合物分解时间条件下的破坏强度，就可算出对应条件下本构关系参数b的值。

由图3不同围压条件下偏应力随应变的变化曲线，研究获取了不同分解时间条件下的破坏强度和极限偏应力，运用公式（10）进一步分析可计算出对应条件下的破坏比，如图7所示。

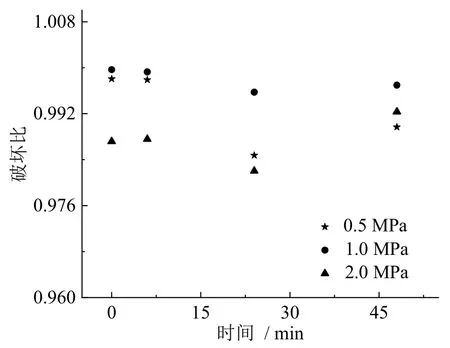
图7 不同围压、不同分解时段条件下沉积物破坏比Fig.7 The dissociation time-dependence curves of the failure ratio Rf under different confining pressures

从图中可以看出，不同围压条件下沉积物试样的破坏比均随着分解时间的延长，表现为先减小后增大的趋势，并且其变化范围很有限。三种围压条件下，破坏比的范围都在0.9969 ～ 0.9981之间，因此可以将其作为一个常量来对待，取这个范围内的中间值0.9975作为破坏比的值，故参数b的表达式为：

由以上分析可知，只要已知围压条件和天然气水合物的分解时间，求出破坏强度qf，即可算出本构关系参数b的值，最终根据a、b的值得出天然气水合物沉积物在相应条件下的本构关系式[20]。

2.3.3 本构关系的验证

首先，在围压为0.5 MPa的条件下，由该本构模型计算得出天然气水合物沉积物试样在水合物分解前后的应力应变关系，并对比验证模拟结果与实验值之间的吻合程度，其步骤如下。

第一步，将σ3= 0.5 MPa代入式（2）～式（4），分别得到三个参数A0、A1、A2的值；第二步，将三个参数A0、A1、A2代入公式（1）中，此处先计算天然气水合物沉积物在分解前的破坏强度值，因此公式（1）中t的值为0；第三步，将σ3= 0.5 MPa代入式（7）和式（8）中，分别得到参数B0、B1的值；第四步，再将参数B0、B1的值代入公式（6），此时，分解时间t为自变量，参数a为因变量，此处计算出天然气水合物沉积物在分解前的参数值，故令t= 0，得出对应的参数a的值；第五步，将第二步得到的破坏强度值代入公式（12），即可得到这一条件下的参数b；第六步，将参数a、b的值代入公式（5），就可以得到该工况条件下偏应力和应变之间的关系，然后即可绘制计算得到的应力应变曲线；第七步，重复上述步骤一至步骤六，分别计算天然气水合物沉积物在分解6 h、24 h和48 h后的各个参数值，然后绘制计算出的天然气水合物沉积物在分解6 h、24 h和48 h后的应力应变曲线。

接着，分别验证围压为1 MPa和2 MPa条件下天然气水合物沉积物分解前后的本构关系。验证方法与围压为0.5 MPa条件下的验证方法一致，最后绘制出三种围压条件下的实验数据和计算数据对比图，如图8所示。从图8可以看出，三种围压条件下，由计算得出的数据绘制成的曲线走势和实验数据曲线基本保持一致。

图8 不同围压下应力应变曲线实验值和计算值对比（温度为 -5℃，应变速率为1 %/min）Fig.8 Experimental and calculated stress-strain curves during hydrate dissociation under different confining pressures

此外，从图8可以看出，天然气水合物沉积物在分解前后的应力应变曲线中，分解时间为48 h时，实验数据曲线与计算数据曲线最为接近，说明拟合计算出的本构关系式更适合应用于具有小强度值的沉积物试样。

本研究构建的本构关系计算出的数据与实验数据存在一定偏差，但偏差范围可以基本忽略（相比岩土力学中的研究结果）；并且随着应变的增大，偏差值呈现越来越小的趋势，从图8中可以看出，当应变大于15%之后，计算数据与实验数据基本上达到完全吻合的状态。因此，本研究构建的本构关系式可以很好地模拟在此围压范围内的天然气水合物沉积物分解前后的应力应变关系。