槽式太阳能集热器热损失计算模型适用性分析*

朱川生，李 靖，李华山，王令宝，马伟斌

（1.中国科学院广州能源研究所，广州 510640；2.中国科学院可再生能源重点实验室，广州 510640；3.广东省新能源和可再生能源研究开发与应用重点实验室，广州 510640；4.中国科学院大学，北京 100049）

0 引 言

槽式集热器（parabolic trough collector, PTC）作为槽式太阳能热发电系统的核心设备，在整个发电系统投资中占比最大，且其性能的优劣直接影响发电系统的热力与经济性能。当前，针对PTC的数学建模大多考虑了影响集热器性能的各方面因素，该方法虽然精度较高，但计算过程较为复杂，其中热损失计算是仿真过程中的重要环节之一[1]。为了提高仿真速度，有研究人员提出了PTC热损失经验模型，即将单位集热器热损失与主要影响因素进行关联，此方法已通过大量的实验验证，并广泛用于发电系统的调节控制[2-4]。

相关研究人员针对PTC热损失模型开展了大量的研究工作。CAMACHO等[4]根据CARMONA[5]在空间太阳能发电站的实验数据，提出了由载热介质温度和环境温度决定的热损失经验公式，随后，ODEH等[6]首次将风速、吸热管壁温以及天空温度考虑在热损失影响因素中，PATNODE[7]首次将太阳直射辐射强度和入射角应用在热损失模型中。DICKES[1]基于美国国家可再生能源实验室的 4 900组实验数据，提出了一种新的热损失经验模型，并与其他3种热损失经验模型进行了对比分析。总体而言，热损失影响因素主要包括：载热介质温度、吸热管壁温、环境温度、直射辐射强度、风速、入射角及其修正系数[8-18]。

目前，PTC热损失的经验模型种类繁多，预测的相关性也各不相同，但各模型都有其特点，因此，模型的准确性和适用性就显得尤为关键。本文基于三组实测数据[12,19-20]对既有文献中公开报道的 PTC热损失经验模型的适用性进行对比验证，并进行相应的误差分析，旨在找到最佳的PTC热损失模型，为PTC的设计和工程应用提供参考。

1 PTC简化模型

PTC主要由槽式抛物面聚光镜、真空集热管组成，其传热过程如图1所示。

图1 槽式集热器传热模型Fig.1 Heat transfer model of PTC

太阳辐射经槽式聚光镜反射后透过玻璃管到达金属吸热管外表面，其中大部分太阳辐射经吸收管的导热最终被载热介质以对流换热的方式吸收实现升温；剩余的太阳辐射经吸收管与玻璃管之间的辐射换热以及二者环隙真空区域残余气体产生的对流换热损失至玻璃管内表面，经玻璃管导热后，最终通过玻璃管外表面与周围空气之间的对流换热以及与天空之间的辐射换热损失到周围环境中。该传热过程涉及了影响PTC性能的各方面因素，计算较为复杂。

在不失模型精度前提下，对模型进行简化，如图2所示，即太阳辐射直接照射至吸热管壁面，且从吸热管壁面通过对流与辐射向大气环境散失的热量采用总传热损失来统一表征。

图2 槽式集热器传热模型简化图Fig.2 Simplified schematic of heat transfer model of PTC

进一步做如下假设：

（1）动能和势能的变化忽略不计[21]；

（2）吸热管管径及壁厚均匀不变[22]；

（3）吸热管外壁面处于高真空氛围，气压一般维持在0.013 Pa以下[19]；

作为早期膀胱癌诊治的标准手段，TURBT在临床上得到了广泛开展和应用，并已经成为各级医院泌尿外科的常规手术。但随之而来的问题是，一些手术相关的不规范也逐渐暴露了出来，成为了制约患者从该手术中临床获益的绊脚石。膀胱癌的诊治过程具有系统性和规范性，TURBT术的开展亦有着严格的标准，其中涉及诸多要点，如肿瘤切除方法、切割深度与范围、闭孔神经反射的预防、特殊部位(如输尿管口、憩室内、电切镜难以到达部位)肿瘤的切除、可疑原位癌的活检、前列腺增生合并膀胱肿瘤的处理、新型显像技术的应用、肿瘤重复电切、以及术后管理等。这些要点的处置与手术效果、患者安全和预后紧密相关。

（4）吸热管内载热介质温度沿其轴向呈线性分布[23]；

（5）吸热管管壁径向导热系数无限大，即忽略吸热管自身的内部导热过程[20]，且壁温沿吸热管轴向呈线性分布[23]；

（6）吸热管内载热介质充分混合，且在同一截面上流速和温度均匀一致，不计边界层影响[24]。

在上述假设条件下，将槽式太阳能集热器沿吸热管长度方向划分成N等份，如图3所示。任意取其中一个微元段Δz作为基本控制体，基于分布集总参数法，微元段Δz的基本控制体的能量平衡方程可以描述如下：

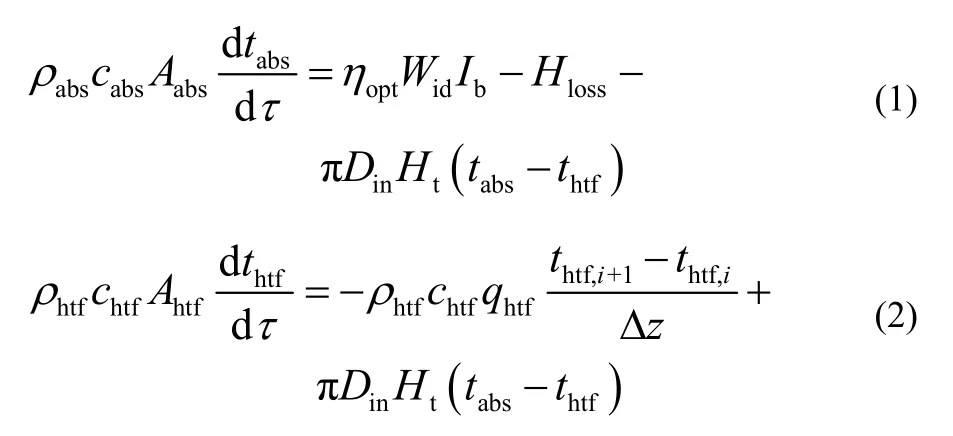
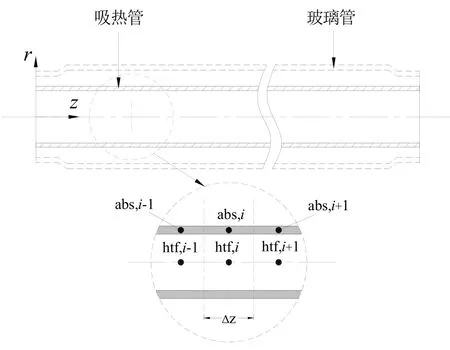
图3 用于传热分析的集热元件和基本控制体Fig.3 Parts of a heat collection element and control volume used for heat transfer analysis

式中：τ表示时间，s；ρ为密度，kg/m3；c为定压比热容，J/(kg·℃)；A为横截面积，m2；t为温度，℃；ηopt为PTC光学效率；Wid为PTC开口宽度，m；Ib为直射辐照强度，W/m2；Hloss为单位长度PTC总传热损失，W/m；Ht为管内对流换热系数，W/(m2·℃)；thtf为载热介质的温度，℃；Din为吸热管内径，m；q为体积流量，m3/s；下标“abs”、“htf”和“amb”分别代表吸热管、载热介质和周围环境。在稳态工况时，吸热管管壁和载热介质温度不随时间变化，式（1）和式（2）左边项为0。

文献调研表明，目前已有的槽式集热器传热总损失经验模型根据主要影响因素的不同可以分为八种类型，具体如表1所示。

表1 槽式太阳能集热器热损失经验模型Table 1 Heat loss empirical models of PTC

值得注意的是，模型2和5采用的单位是W，模型3和4采用的单位是W/(m2·℃)，模型8和9采用的单位是W/m2，而式（1）中Hloss的单位为W/m。因此，为使量纲统一，在分析计算时，参考模型原文，以W、W/(m2·℃) 和W/m2为单位的模型分别按式（3）、式（4）和式（5）进行转换：

2 数据来源

为对比分析上述模型的准确性和适用性，基于三组不同的PTC实测数据进行对比分析：第一组是美国SEGS LS-2型集热器，采用导热油Syltherm 800作载热介质，由DUDLEY等[19]在SNL完成，这也是目前众多文献中参考最多的实验结果；第二组集热器由18根吸热管（PTR70）组成，尺寸规模相对较大，采用导热油Syltherm 800作载热介质，由VALENZUELA等[12]在西班牙PSA实施测试；第三组集热器尺寸规模较小，采用水作载热介质，由ALFELLAG于2014年2月19日在美国佛罗里达州的安柏瑞德航空航天大学（Embry-Riddle Aeronautical University, ERAU）完成测试，实验装置包括集热器、循环泵、储热罐和热交换器等，所测得的实验系统最大效率为30%[20]。本文所采用的实验数据共计32组，其中SNL 8组、PSA 10组和ERAU 14组。

三组实验工况均为稳态结果，不同的是，DUDLEY的实验测试均以零入射角为基准，温度取值范围比较大，为100 ～ 450℃；VALENZUELA等测试时入射角在一天中随时间变化，而温度取值范围相对比较集中，为290 ～ 400℃，且不考虑风速对实验结果的影响；Alfellag的实验测试中其流量固定为6.309 × 10-5m3/s（1 GPM，1加仑每分钟），其综合考虑了入射角/太阳直射辐射强度和风速随时间变化对测试结果的影响，且其载热介质温度比较低，在30 ～ 50℃范围内，这也是实际运行操作中会遇到的PTC运行温度较低的工况。三种集热器的具体参数如表2所示。

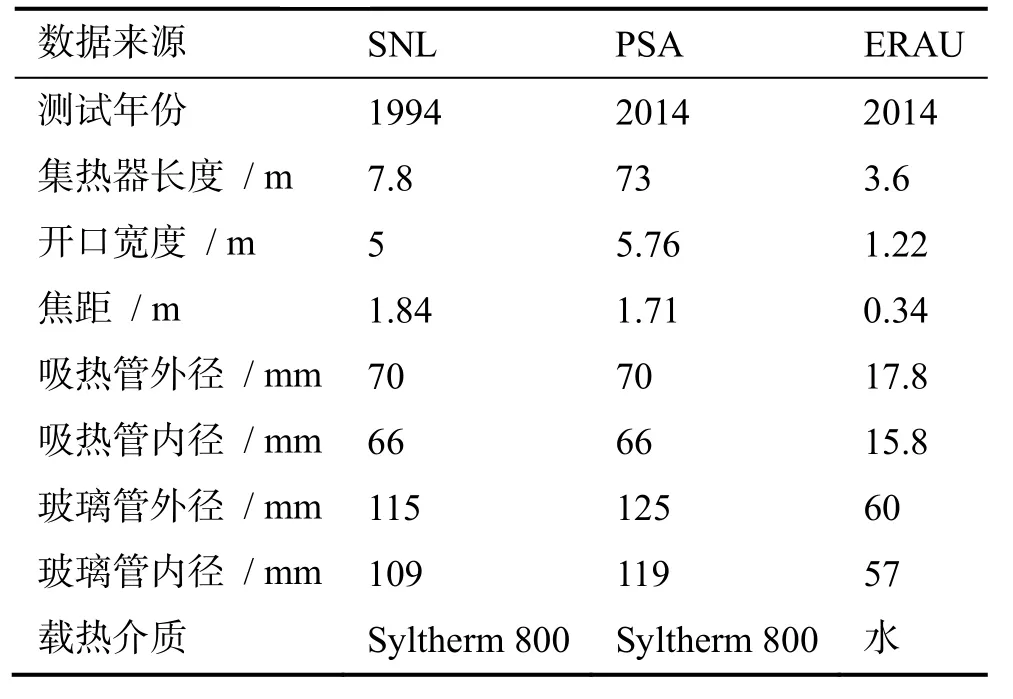
表2 用于模型评价的集热器参数Table 2 Collector parameters for model evaluation

3 计算结果与分析

3.1 评价方法

为了对比分析上述16个模型的优劣，引入4个误差评价指标，分别为平均绝对百分比误差MAPE、平均偏差MBE、均方根误差RMSE和相关系数R2，计算方法如式（6）～ 式（9）所示。

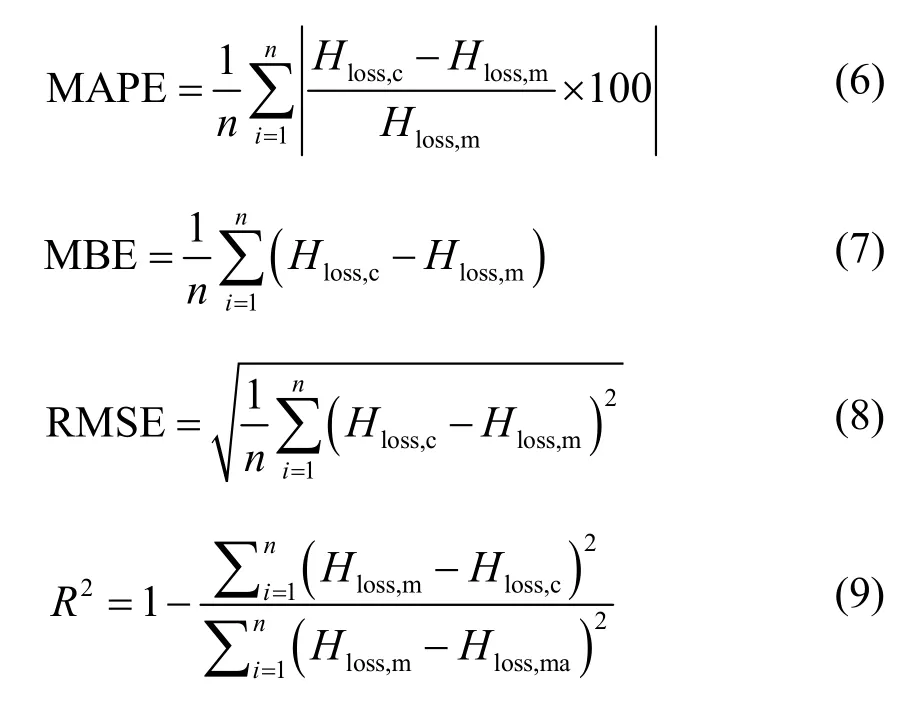
式中：Hloss,c为模型计算值；Hloss,m为实测数据；Hloss,ma为实测数据的平均值；n为数据总数量。

MAPE表示绝对百分比误差平均值的大小，MAPE越小越好；MBE表示计算值偏离测量值的多少，MBE越接近于0越好；RMSE表示计算值在实测值周围的离散程度，RMSE越小越好；R2表示回归模型与实测数据的拟合程度，R2越接近于1越好。

3.2 适用性分析

基于Matlab软件，对三种集热器分别建立数学模型，计算16个模型在不同测试点的PTC出口温度，并计算相应的 MAPE、MBE、RMSE、R2。为探究不同测试点不同载热介质工况温度范围模型的适用性，进一步计算16个模型基于全部实测数据的整体均方根误差和相关系数，并给出了PTC出口温度计算值和实测数据的相关性，结果见图4 ～ 图6。

通过不同测试点实测数据与模型计算结果的统计表现进行分析，可以观察到：对于SNL的实测数据，PTC载热介质工况温度在100 ～ 450℃范围内的实测数据，除Dickes模型和实验结果出现了非常大的偏差外，其他模型均有非常好的适用性，R2在99.476%以上，其中计算精度最高的是WANG等模型，其统计表现为：MAPE、MBE、RMSE、R2分别为 0.251%、0.690℃、0.763℃、99.993%。对于PSA的实测数据，PTC载热介质工况温度在290 ～400℃之间，除Patnode模型吻合度较高外，其他15个模型均表现较差，RMSE在5℃以上，R2在95%以下，Patnode模型的统计表现如下：MAPE、MBE、RMSE、R2分别为 0.595%、-0.179℃、2.505℃、99.114%。对于ERAU的实测数据，PTC载热介质工况温度在30 ～ 50℃范围内的实测数据，与之前测试点不同的是，Dickes模型计算结果和实测数据基本重合，表现出了很高的计算精度，远优于其他模型，Dickes模型的统计表现如下：MAPE、MBE、RMSE、R2分别为0.595%、-0.0124℃、0.318℃，99.411%。除 Dickes模型外，其他模型得到的结果普遍低于ERAU的实验测试结果，MAPE在3%左右，MBE在 1.5℃左右，RMSE在 1.5℃左右，R2在84.175% ～ 89.211%之间。

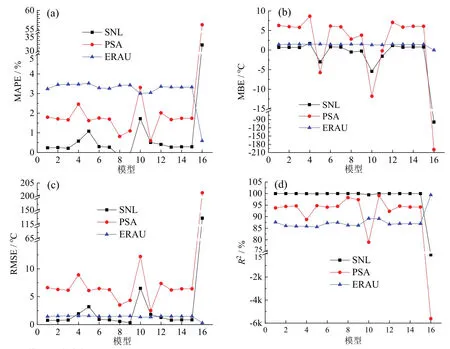
图4 16个经验模型的统计表现：（a）MAPE；（b）MBE；（c）RMSE；（d）R2Fig.4 Statistical performance of 16 empirical models：(a) for MAPE; (b) for MBE; (c) for RMSE; (d) for R2

基于全部实测数据的模型相关系数R2与RMSE如表3所示。综合三组实测数据，除Dickes模型外，其他模型统计结果均很好，R2在99.729%以上，PTC出口温度均方根误差 RMSE在 7.615℃以下。其中适用性最好的是Patnode模型，其R2以及PTC出口温度均方根误差RMSE分别为99.983%和1.900℃。

表3 基于全部实测数据的模型相关系数R2与RMSETable 3 RMSE and R2 of the examined modes based on all measured data

Dickes模型和Patnode模型的PTC出口温度计算值和实验值的对比如图5和图6所示，可以看出，Dickes模型与温度介于30 ～ 50℃范围内的ERAU实测数据高度吻合，但与其他两组实测数据吻合较差，导致整体R2相对偏低，RMSE较大。Patnode模型的PTC出口温度的计算值和实测数据非常吻合，亦表明了在温度范围为30 ～ 450℃时，Patnode模型计算精度最高，适用性最好。在热损失回归公式中，Patnode将太阳直射辐射强度、入射角以及载热介质温度作为影响PTC热损失的决策量，表明了这三个变量对PTC热损失的有效估计是极为关键的。

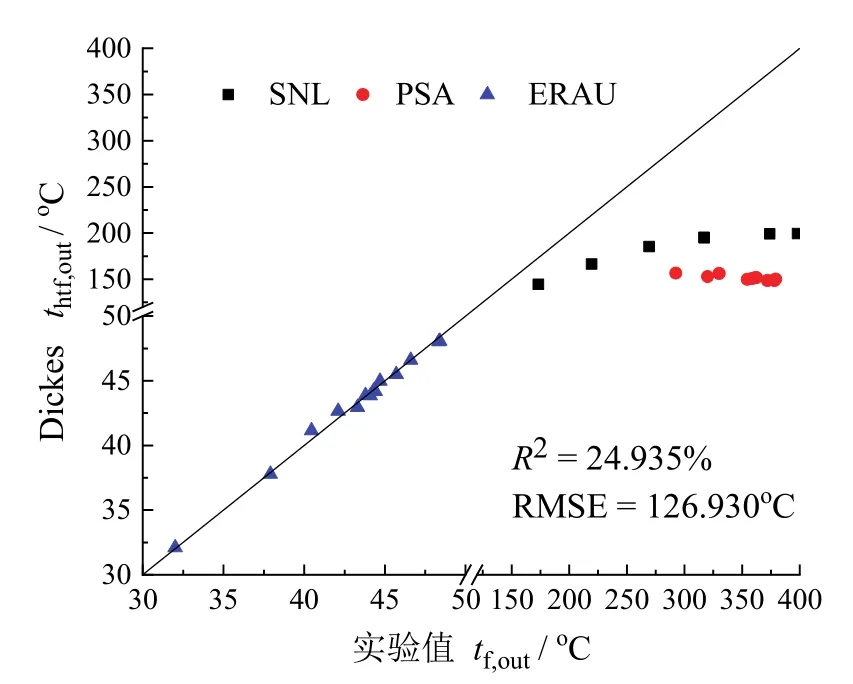
图5 Dickes模型计算值与实验值比较Fig.5 Comparison of calculated results from Dickes model with experimental data

图6 Patnode模型计算值与实验值比较Fig.6 Comparison of calculated results from Patnode model with experimental data

4 结 论

基于三组不同的PTC实测数据对16个热损失模型的适用性进行了对比验证，结论如下：

（1）不同PTC载热介质工况温度对应的最佳热损失模型不同。基于SNL的实测数据, PTC载热介质工况温度为100 ～ 450℃范围内时，除Dickes模型和实测数据出现了非常大的偏差外，其他模型均有非常好的适用性，R2在99.476%以上；基于PSA的实测数据，PTC载热介质工况温度为290 ～ 400℃范围内时，Patnode模型适用性最佳；基于ERAU的实测数据，PTC载热介质工况温度为30 ～ 50℃范围内时，Dickes模型适用性最佳，计算结果和实测数据基本重合，统计表现 MAPE、MBE、RMSE、R2分别为0.595%、-0.0124℃、0.318℃、99.411%，表现出了很高的计算精度，远优于其他模型，其他模型相关系数均在90%以下。

（2）综合而言，当PTC载热介质工况温度在30 ～ 450℃范围内时，除Dickes模型与实测数据出现了较大偏差外，其他模型均有非常好的适用性。相比于其他模型，Patnode模型的计算精度最高，统计表现MAPE、MBE、RMSE、R2分别为1.645%、0.129℃、1.900℃、99.983%。表明对于PTC热损失的计算，Patnode模型具有很高的准确率和很好的适用性，同时也说明直射辐射强度、入射角以及载热介质温度对PTC热损失的大小起着决定性的作用。