三种设计，各美其美——一次“余角、补角、对顶角”同课异构活动引发的思考

☉江苏省滨海县第一初级中学 陈月玲

近期，在一次市级同课异构活动中，笔者有幸聆听了三节“余角、补角、对顶角”第1课时的现场课，听后受益匪浅.下面就三位老师针对对顶角和互余（互补）的性质所做的设计进行简单介绍，并给出自己的思考，不当之处，敬请指正.

一、三种设计

1.第一位教师的设计

第一位教师虽然按照教材进行设计，但是对教材内容进行了大胆取舍和改进，具体如下：

首先，让学生观察现实生活中的一组图片，引导学生发现其中蕴含的余角、补角的关系，然后启发学生去发现现实生活中更多的类似的实物，进而得出余角和补角的概念.在此基础上，再让学生去发现和探究对顶角的概念和性质.

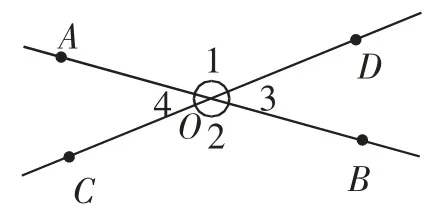
图1

问题1：∠1和∠2的顶点和两边有什么位置关系？

问题2：∠1和∠2有什么数量关系？如果将直线AB绕点O转动，上述关系还成立吗？∠3和∠4呢？

问题3：∠1和∠3有什么数量关系？还有其他成对的角有这样的数量关系吗？

在处理余角（补角）的性质时，将教材提供的情境以动态的形式呈现，并在教材的基础上进行简单改编，具体设计如下：

图2

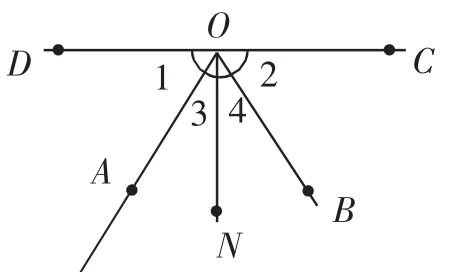
图3

将图2简化为图3，ON与CD相交所成的∠DON和∠CON都等于90°，且∠1=∠2.

问题1：有哪些角互为余角？∠3和∠4有什么关系？为什么？

问题2：有哪些角互为补角？∠AOC和∠BOD有什么关系？为什么？

2.第二位教师的设计

第二位教师在处理“对顶角”时基本采用了教材呈现的方式：

将剪刀的构造看作两条相交直线（如图1），进而提问：

问题1：∠1和∠3有怎样的位置关系？∠1和∠2呢？

问题2：分别量一下角数，∠1和∠3的度数有什么关系？∠1和∠2呢？在剪刀剪东西的过程中，这个关系还保持吗？为什么？

在此基础上，教师引导学生得出对顶角的概念和性质.

在处理余角（补角）的性质时，也没有采用教材呈现的方式，而是先以一个微课的形式向学生介绍了“入射光线、反射光线和法线”的相关知识，实现了与教材提供材料的“异曲同工”.具体设计如下：

图4

图5

将图4简化为图5，ON与CD相交所成的∠DON和∠CON都等于90°，且∠1=∠2.

问题1：图中哪些角互为余角？

问题2：∠3和∠4有什么关系？为什么？

问题3：图中哪些角互为补角？

问题4：∠AOD和∠BOC有什么关系？为什么？

3.第三位教师的设计

第三位教师则采用了一种全新的处理方式，将“画图”贯穿于课堂教学的整个过程，给人一种耳目一新的感觉.

画图1：（1）画直线AB，（2）画直线CD，（3）假设它们的交点为点O，（4）将形成的四个夹角分别表示为∠1、∠2、∠3和∠4（如图1）.

在画图1的基础上，采用与第一位教师或第二位教师类似的方法引导学生自主探究对顶角的定义和性质.在得出互余和互补的概念后，再次引导学生画图.

画图2：（1）先画锐角∠AOB，（2）作CO⊥OB，垂足为点O，（3）作DO⊥OA，垂足为点O（如图6）.

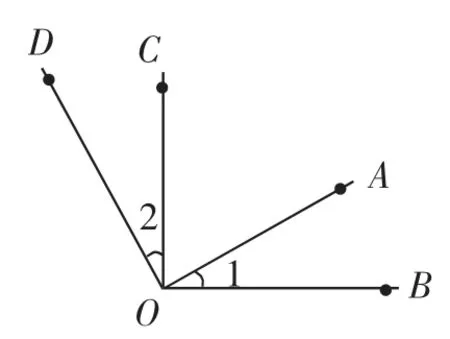
图6

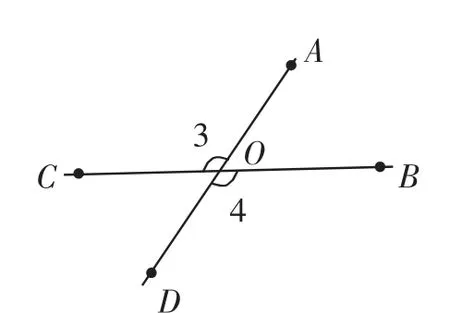
图7

问题1：图中哪些角互为余角？

问题2：∠1和∠2有什么关系？为什么？

问题3：你能得出什么结论？

通过上述三个问题引导学生得出：同角的余角相等，然后抛出问题4：

问题4：等角的余角有什么关系呢？你能用画图的方式进行说明吗？

画图3：（1）画∠AOB，（2）反向延长OB到点C，（3）反向延长OA到点D（如图7）.

问题1：图中哪些角互为补角？

问题2：∠3和∠4有什么关系？为什么？

问题3：你能得出什么结论？

通过上述三个问题引导学生得出：同角的补角相等，然后抛出问题4：

问题4：等角的补角有什么关系呢？你能用画图的方式进行说明吗？

二、各美其美

1.贯彻课标，落实理念

《义务教育数学课程标准（2011年版）》指出：情境的创设可从生活现实、数学现实或其他学科现实进行，上述三位教师的设计可以说是对上述理念的积极践行.

第一位教师采用了学生熟悉的给人以平行或相交感觉的大量实物得出平行线和相交线的定义，在研究余角（补角）的性质时则采用了学生熟悉的“台球游戏”，以上所选情境贴近学生的现实，可以说是一种很好的从“生活现实”创设情境的尝试.

第二位教师除了与第一位教师类似，以生活现实的形式引出平行线和相交线，在后续教学中还采用微课的形式向学生介绍“入射光线、反射光线、法线”的相关知识，这是一种“其他学科现实”，可以看出与第一位教师的设计异曲同工.

第三位教师则完全以作图的形式贯穿整节课，这是一种从数学内部出发，发现问题，进而提出问题和解决问题的方式，这是一种典型的以数学现实创设情境的有益尝试.

2.源于教材，用教材教

教材是专家和一线教师集体智慧的结晶.

本节课主要涉及对顶角的概念和性质、互余（互补）的概念及性质，可以看出本节课的课时容量非常大，基本上融合了教材两个课时的内容.但是，执教教师并没有畏难情绪，而是迎难而上，结合教材的设计特点设计出了三节“源于教材，用教材教”的优秀课例.

三、实践跟进

同课异构活动结束后，笔者所任教的班级也要上这节课，此时在综合上述三节课例优点的同时，笔者给出了另外一种设计，教学中重在培养学生的分类意识和类比的数学思想，在学生刚刚接触几何学习的开端“埋下一粒种子”，倾心浇灌，静待花开.

如图1，所形成的四个角中，两两之间有什么关系？（提示：可以从数量和位置关系两个角度回答）

显然，这是一种开放性的设问，可以很好地锻炼学生的思维能力，更有利于培育学生的核心素养，而且在教学中也收到了意想不到的教学效果.

期待更多的一线教师加入进来，针对本节课设计出更多优秀的案例，为实现初中数学课堂教学的百花齐放贡献一份自己的力量.