于无声处听惊雷，重组习题观素养——以“矩形（第1课时）”教学设计为例

☉浙江省湖州市志和中学 沈雪强

在《义务教育数学课程标准（2011年版）》中，明确规定：内容设计要有弹性，关注不同学生的数学学习需求；课后习题的选择与编排应突出层次性；增加的内容应注重数学思想方法，注重学生的发展，有利于学生认识数学的本质与作用.在数学教学中，我们要理解编者编写教材的真正意图，要学会从教材例题、习题中渗透知识和提炼学生的数学素养，更要深入研究它和恰当运用它，因此就必须要对例题、习题进行适当的重组.

以浙教版八年级下册第五单元“矩形”的第1课时为例，本人有幸参加了湖州市数学优质课评比，并获得一等奖，现将本课的教学设计和反思进行整理，请读者批评指正.本设计主要对课本上的例题、习题进行了适当的重组与创新，并进行方法的提炼与数学思想的渗透，在降低矩形两个性质定理运用难度的同时，逐步向学生渗透数学素养.

一、教学目标及学情分析

1.教学目标

（1）理解性质定理“矩形的四个角都是直角”“矩形的对角线相等”，并会进行初步应用.

（2）经历探索矩形过程，发展学生合情推理的意识，掌握几何思维方法.

（3）培养严谨的推理能力，体会逻辑推理的思维价值，并学会欣赏美的事物.

2.学情分析

这是学习平行四边形知识后的第一课时，同时，学生也已经对特殊三角形具有一定的认识，因此具备初步的逻辑推理能力及书写表达能力.在本节课的开端，已经解决了矩形的两个性质定理的证明，接下来就是要通过例题和习题来应用它.

二、原题重现

例1 已知：如图1，矩形ABCD的对角线AC、BD相交于点O，∠AOD=120°，AB=4cm.

（1）判断△AOB的形状.

（2）求矩形对角线的长.

课内练习2：如图1，矩形ABCD的两条对角线相交于点O，图中有多少对全等三角形？把它们写下来.

课内练习3：已知矩形的周长为56，对角线的交点到短边的距离比到长边的距离大4，求矩形的各边长.

作业题3：已知：如图2，过矩形ABCD的顶点作CE∥BD，交AB的延长线于点E.

求证：∠CAE=∠CEA.

作业题5：利用矩形的性质定理“矩形的对角线相等”证明：直角三角形斜边上的中线等于斜边的一半.

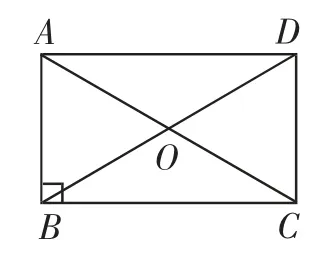
图1

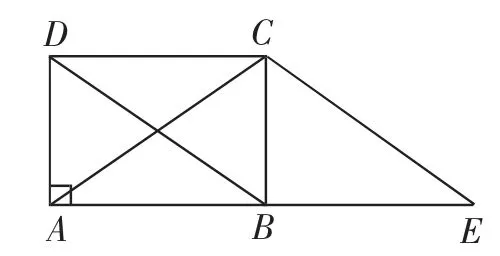
图2

三、教学实施

观察：（Ⅰ）如图3，在矩形ABCD中，两条对角线相交于点O，则图中有哪些特殊三角形？

图3

设计意图：题目来源于课内练习2，做适当的改变：找全等三角形变为找特殊三角形.初步建立起矩形与三角形的联系.通过寻找特殊三角形，寻本溯源，发现矩形的两个性质定理：矩形的四个角都是直角、矩形的对角线相等，就是两类特殊三角形的根源.加深理解定理的同时，也使定理得到初步应用.同时，通过黑板板书，规范证明等腰三角形的过程（任选一个如△AOB），为后续证明做好准备.

（Ⅱ）如果∠AOD=120°，你能判断△AOB的形状吗？

设计意图：来源于书本例题.在（1）的基础上，学生判断△AOB的形状更自然流畅，也让学生明白等腰三角形到等边三角形所需的条件.同时，将（1）的板书过程补充完整，这样就成了原例1.

（Ⅲ）满足∠AOD=120°的条件不变，如果AB=4cm，求对角线AC的长.

设计意图：来源于课本例题第（2）问，突出特殊三角形的存在，将思考的问题转换到特殊三角形，逐步渗透转换思想.

追问1：你能求出此时矩形的周长和面积吗？

设计意图：通过求BC（或AD），将问题集中到Rt△ABC中，以便学生观察，发现熟悉的数学结论.

追问2：观察图4，你能想到直角三角形的哪个结论？

设计意图：来源于书本课后作业第5题.将新知化归为旧知，更易为学生所掌握，同时加深了学生对新知的理解.

通过上述问题串，在强化应用两个性质定理的同时，逐步将学生的思维引导到特殊三角形，从而让问题的转化水到渠成.

变式1：如图5，已知矩形的周长为28cm，对角线的交点到短边的距离比到长边的距离大1cm.求矩形的各边长.

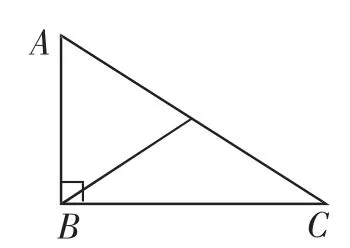
图4

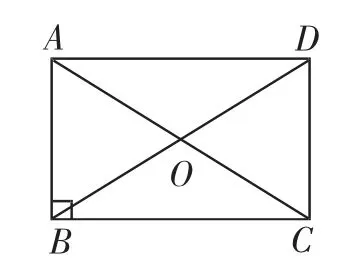
图5

设计意图：来源于课内练习3.通过添加辅助线，如图6，过点O作OE⊥AB，OF⊥AD，将问题再次回归到特殊三角形，结合等腰三角形三线合一，得到E、F为中点，从而得到OE、OF分别是AD、AB的一半，所以设OF=x，则OE=x+1，得到方程2x+2（x+1）=14，从而使问题得以解决.在解题中，渗透方程思想，让问题的解答变得更容易.

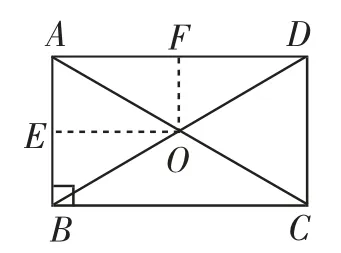
图6

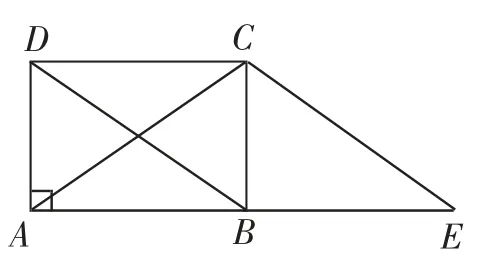
图7

变式2：如图7，如果过矩形ABCD的顶点作CE∥BD，交AB的延长线于点E，求证：∠CAE=∠CEA.

设计意图：来源于课后作业第5题.将基本图形做复杂处理，让学生在发现基本图形的过程中，回顾相关知识，以便将各种知识相关联，从而想到解决问题的关键所在.本题在于告诉学生，可以从题设的矩形出发，发散思维，进行联想，也可以从结论出发展开联想，只要得到AC=CE=BD即可.通过这样的设计，让学生学会“联想—猜测—证明”的解决方法.当然，如果课堂时间宽裕，可以尝试一题多解，发散思维.

四、反思

1.重组例题，完善知识的认知结构

例题重组，是以教学目标为先导，抓住教材所要解决的基本问题及其基本练习.本节课的教学目标是矩形的性质定理.在教学过程中逐步渗透，不断强化.将例1进行重组与创新，提取课内的练习2作为观察（Ⅰ）呈现.通过将原图形（矩形对角线相等的证明图形）添加对角线的交点，得到新图形，让过程自然、流畅，便于学生观察得到两个性质定理的存在，从而使问题的指向更清晰.观察（Ⅱ）和观察（Ⅲ）是原始例题，感受矩形与三角形知识的紧密联系，以便完善几何中三角形与四边形的知识系统.另外，安排“追问”，将问题集中到直角三角形，这样学生在回忆和应用知识的过程中，既可以感受到知识之间的联系和区别，又可以完善知识的认知结构.

2.凝练方法，提升解决问题的能力

不管课程改革如何深化，课堂教学如何改变，有两项基本工作是不变的：一是研究学生，二是驾驭教材.但这都是为了让学生能够更好地思考问题和解决问题.在设计中安排变式2，就是让学生学会从条件和结论出发去寻找分析问题和解决问题的方法，教师再提炼方法：将仔细联想（条件和结论），大胆猜测，具体证明，凝练为“联想—猜测—证明”的方法，从而帮助学生提升解决问题的能力.

3.渗透思想，发展学生的核心素养

数学思想是数学知识的核心，是学生将知识转化为能力的桥梁，更是学生学科素养的核心.通过观察（Ⅰ）至（Ⅲ），渗透转化思想，有助于学生认清知识结构，从而将问题抽象成一般的数学模型——特殊三角形.另外，通过追问，便于学生发现问题集中在直角三角形中，借助几何直观，有助于对数学问题发挥直观想象，为后面的变式2的研究提供思维上的借鉴，从而发展核心素养.另外，通过变式1，导出方程思想，将数学知识内化为等腰三角形的三线合一，从而得出中位线，并借助方程提升学生的逻辑推理能力.

从本课的案例来看，往往将课堂教学与数学素养结合的追求是一种现阶段理想化的课堂，理想的数学课堂是多维度、多模式的，核心素养更是全方位、立体化的，将数学学科核心素养与理想的数学课堂教学有机整合，是数学课堂教学一次全新的尝试.从现有的教学来看，笔者认为今天这种例题重组教学是有意义的，这与高效课堂的理念不谋而合.理想的数学课堂因为各种各样的原因，尚不能完全普及到各年级的教学实践当中，但是教师对于新一轮课程标准的理解和课程改革的发展趋势，有需要超前一步的探索勇气，这种探索有助于教师自身对于教学有更高层次的理解和更专业化的发展，有助于学生数学素养的提高，更让数学教学站在了系统的高度，让学生获得了前所未有的视野，这便是一种成功.

总之，数学例题往往只提供一种思路，或者只承担一种价值，但我们在例题教学时，要学会欣赏与批评，更要通过重组与创新，来提升课堂效率，发展学生的数学学科核心素养.