基于障碍凸化的改进环流APF路径规划
2019-10-31贾正荣王航宇卢发兴
贾正荣,王航宇,卢发兴
海军工程大学 兵器工程学院,武汉 430033
人工势场法(Artificial Potential Field, APF)是一种用于路径规划的方法,具有形式简单、实时性好的特点,能够用于静态路径规划与动态路径规划问题中[1-2],并且可以并行求解以提高效率[3]。其基本原理是将终点作为引力源,障碍作为斥力源,生成一个空间内的势场,移动平台沿着势场方向运动以规避障碍并到达终点[4-8]。
人工势场法的一个主要问题是局部极小值问题:由于障碍形状多样,可能在空间中产生引力与斥力的平衡点,平台到达这一平衡点后将无法逃逸而导致路径规划无解。
现有文献为解决APF方法的势场局部极小值问题,提出了各种改进方法。文献[9]通过引入目标与机器人的相对距离,将原有斥力势场函数乘以一个距离因子,使机器人在目标位置处合力为零。针对多边形障碍,引入一种边缘探测方法,作多边形的外接圆,从而将多边形障碍转换为点障碍。文献[10]将作为势场模型的Gaussian函数进行了适当变形,使其能更准确地反映势场环境。通过分析震荡现象产生的原因,以及局部极小值点的特点,将粒子群算法引入到势场的探测过程中,在此基础上提出了等位线法用于逃逸局部极小值。文献[11]提出了通过增加虚拟目标点和原目标点共同对机器人产生引力的方法来解决传统人工势场法中出现的局部极小点问题,然而得到的路径结果具有一定的振荡现象。文献[12-14]利用模拟退火算法解决人工势场法的局部极小点问题。文献[15]针对传统人工势场法应用于移动机器人路径规划存在的缺陷,建立了改进的人工势场模型;使用势场强度代替力矢量进行路径规划;在障碍物的斥力势场中添加系数项,解决障碍物与目标点过近导致的目标不可达问题;考虑移动障碍物速度与机器人速度的影响,将速度信息引入到势场函数中;引入“填平势场”引导机器人走出局部极小点。文献[16]提出添加附加控制力的方法,当机器人所受的斥力与吸引力在一条直线上时,对机器人施加一个依赖于障碍物的控制力,使机器人尽快跳出局部极小点。文献[17]通过在势场局部极小值点附近增加虚拟障碍以改变附近的势场分布。文献[18]通过粒子群优化算法解决势场局部极小值问题。文献[19]增加控制力的作用规避无解的情况。文献[20]则通过改变障碍的形状以提高路径可解的概率。文献[21]通过引入一种引力势场选择策略以规避势场的局部极小值。文献[22]通过引入优先策略以更改APF算法解决路径规划无解的问题。文献[23]通过引入引力源与斥力源之外的控制外力以优化路径规划求解。文献[24]通过引入虚拟路径点产生外力以避免平台进入局部极小值。文献[25]提出了基于改进人工势场的防碰撞控制方法,引入辅助斥力势来提高碰撞规避的效果。文献[26]为解决传统人工势场法无法避免的局部极小问题,将局部极小分为两类,分别给出两类极小值的判定定理及方法,仍然使用了一种增加的“填平势场”用于改善局部极小值问题。文献[27]研究全局静态环境下移动机器人路径规划,提出一种改进势场蚁群算法,该方法针对离散(网格)地图内的路径规划。文献[28]提出了一种基于滚动时域控制和快速粒子群优化方法,将路径规划问题转化为优化问题,并将斥力场引入到代价函数中,提升路径安全性。与之类似,文献[29]也采用了一种预测控制的方法优化路径。
可见,一般通过3种方法解决APF方法的势场局部极小值问题,一是在势场局部极小值附近引入选择策略,这种方法在障碍数量较小时易于实现,但是当障碍数量增多后,策略将变得较为复杂,同时,当平台位于多个障碍之间且并未陷入局部极小值时,路径可能产生较为明显的振荡;二是采用智能算法寻找逃出势场局部极小值的路径,这种方法需要大量的运算,掩盖了APF实时性好的特点;三是增加引力或斥力源以改变势场分布情况,但是如何增加引力或斥力源对于是否可解有很大的影响,若引力或斥力源增加失当,则可能造成无解或路径振荡。
另外,现有方法还采用了预测控制的思路[28-29],在路径规划的每个时间步长上展开一个预测窗口,并设立若干优化指标,滚动地优化路径以取得更好的效果。但是如果能够避免传统APF方法局部极小值导致无解的问题,在理论上将会进一步提升预测控制路径规划的效率。
除此之外,现有方法在路径规划过程中,为了避免凹障碍的不利影响,一般都对障碍采用了凸化处理[9],但是当障碍数量较多、彼此相交情况复杂时,需要一种更为详尽、全面的方法进行障碍的凸化处理。
综上,为了提高APF方法的实用性,需要解决的问题主要有两点,一是在复杂障碍环境内应用APF方法的问题,二是因势场局部极小值导致无解的问题。
1 问题描述
移动平台需要在障碍空间内运动至指定的目标位置,移动平台的运动受到转弯半径的约束,其转弯半径不能小于最小转弯半径rmin。
实际环境中出现的大部分障碍都能够通过多边形障碍、圆形障碍以及它们的组合表示。多边形障碍包括凸多边形与凹多边形,可以描述环境空间中的禁飞区、一般实体障碍等。圆形障碍不仅可以表示禁飞区、实体障碍,而且可以描述威胁区域或敌方火力作用区域。
在使用APF进行路径规划过程中,由于障碍存在凹陷,当平台进入这些凹陷区域后,斥力与引力的平衡会导致平台进入局部最小值点,从而无解。
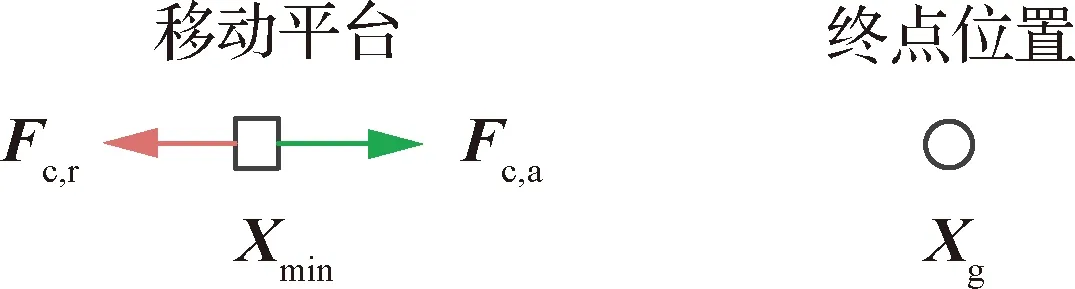
凹障碍的出现主要有2种情况,分别为凹多边形障碍与相交的凸障碍产生的凹区域,如图1和图2所示。因此,可以将凹障碍凸化以避免APF方法无解的问题。另外,在凸多边形障碍环境中,传统APF方法仍然存在局部极小值的问题,比如当凸多边形的边界与平台-目标位置连线垂直时,合势场也有可能为0,如图3所示。因而还需要对APF斥力势场进行一定的改进,使斥力势场沿着多边形障碍绕行,如图4所示,从而避免图3中的情况。
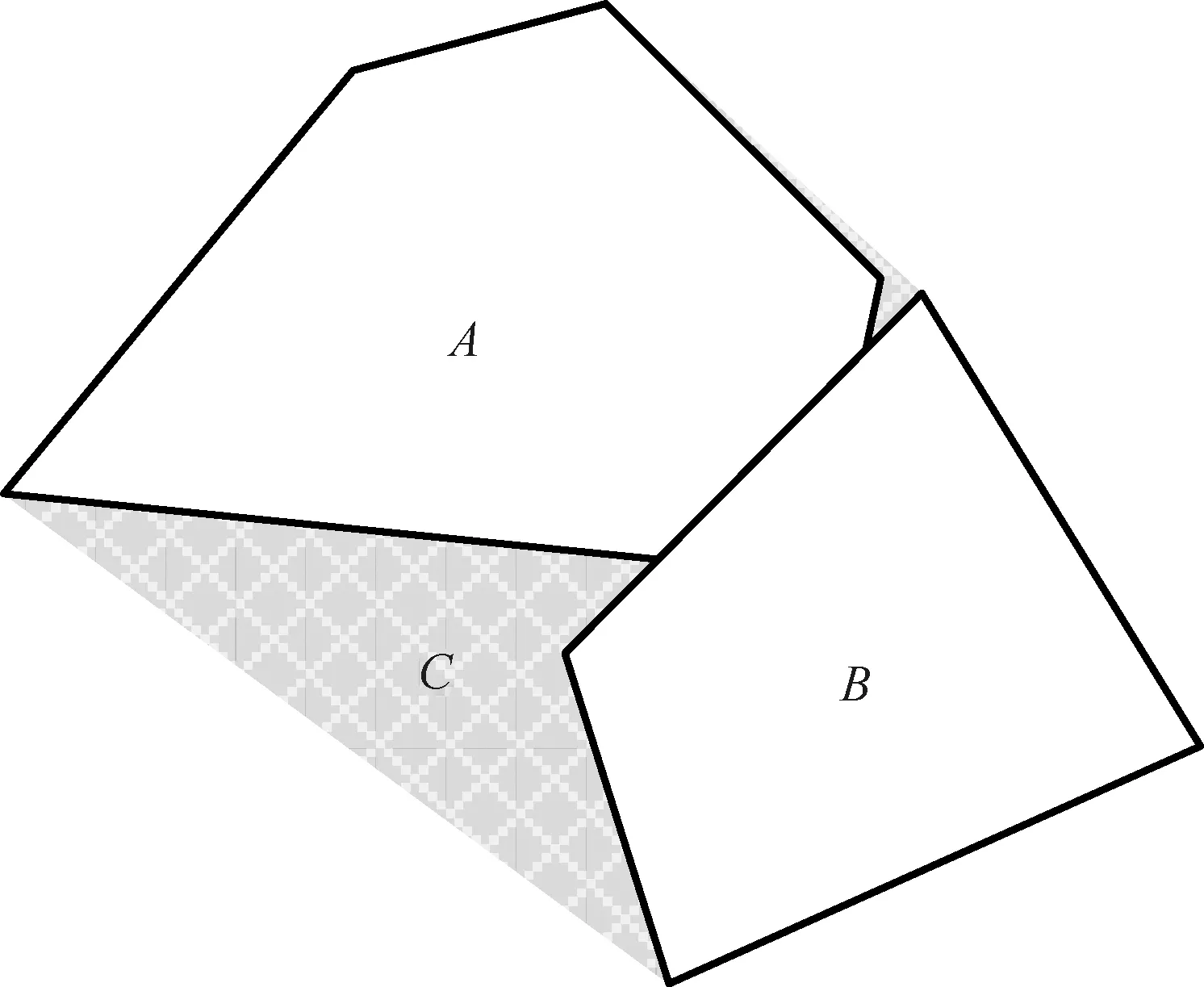
图2 相交凸障碍产生的凹区域
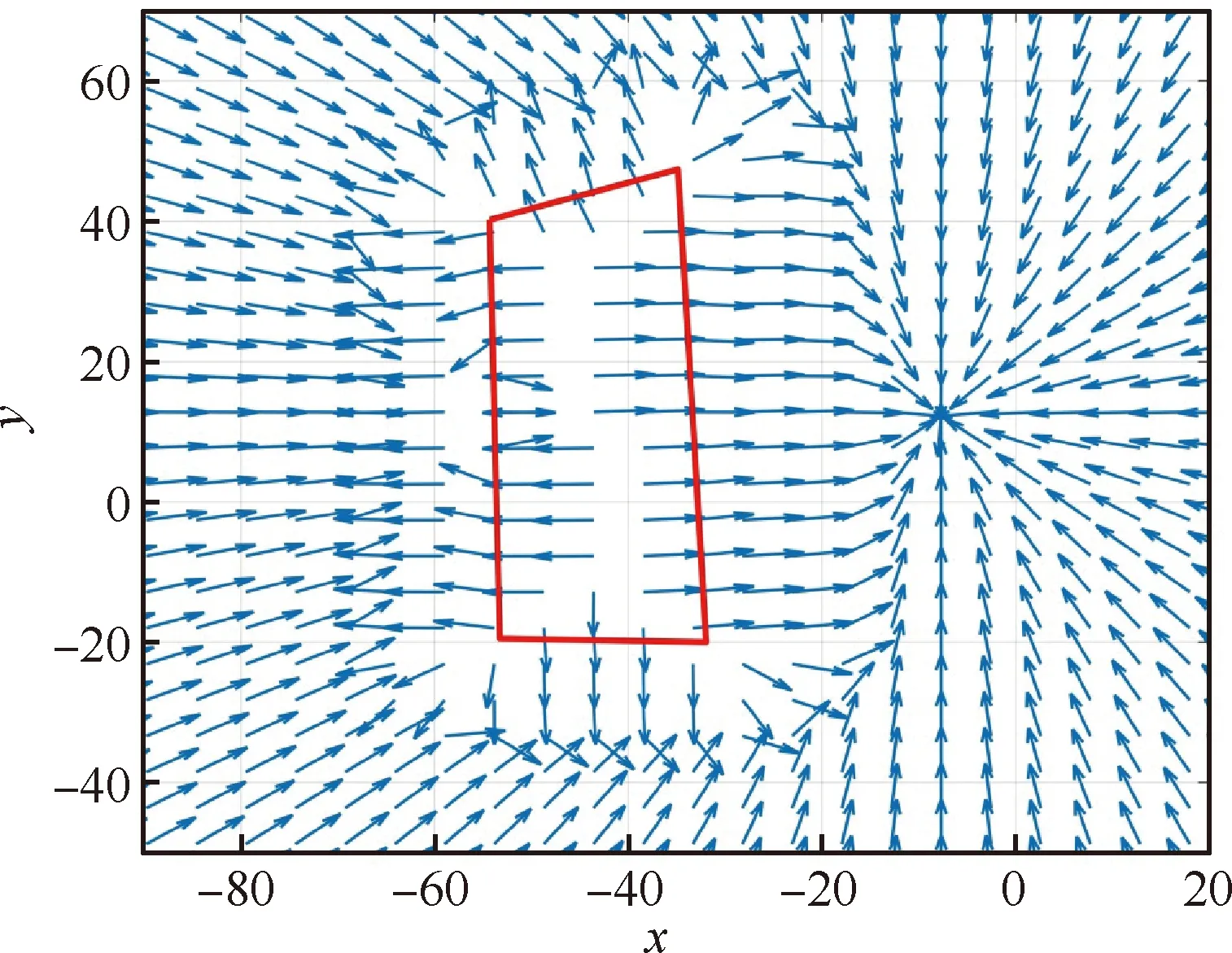
图3 合势场为0的情况

图4 环绕多边形障碍的势场方向
2 环流APF方法
2.1 平台运动模型
设平台状态向量为Xp=[xp,yp,vp,βp,ωp]T,xp、yp为平面内的位置坐标,vp为速率,βp为航向,ωp为角速度,在离散形式下,平台的运动可以描述为
(1)
式中:Δt为时间步长;ap为加速度;φp为角加速度,通过调整平台航向来控制平台的路径。
由于本文仅涉及单一平台在静态障碍环境中的运动,不涉及坐标的变换,因此可以以平面内任意一点作为坐标原点建立惯性坐标系,全文中的坐标均在同一个坐标系下描述,后文中将不再强调坐标系。
2.2 APF方法路径规划
APF方法可以实时生成规避障碍的路径。在APF方法中,终点产生引力,障碍产生斥力,合力的梯度即势场决定了平台的运动方向。
设终点位置为Xg=[xg,yg]T,平台当前位置为Xs=[xp,yp]T,障碍为Ωi,障碍的数量为nob,则APF方法构建斥力Ur为
(2)
引力Ua为
Ua=fa(Xs,Xg)
(3)
则合力为
U=Ur+Ua
(4)
梯度场为
(5)

(6)
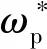
|ωp|≤ωmax
(7)
从而实际的角速度应当为
(8)
式中:sign()为符号函数,即
(9)
2.3 引力与斥力构建
在本文的分析中,传统APF方法与基于环流斥力势场的改进APF方法仅梯度构建形式不同,引力与斥力的函数相同。
对于平台位置Xs,终点位置Xg,凸障碍Ωi以及其与Xs的最近点Xd,i,引力Ua为
(10)
式中:Ua,max为一常量,为使Ua在Xs的主要活动范围内取值为[0,1]之间,可以取
Ua,max=kmax|Xg-Xs,0|
(11)
式中:Xs,0为平台Xs的初始位置;kmax为大于1的常量。
斥力Ur为平台Xs与每个障碍Ωi的斥力和:
(12)
式中:Ur,i为平台Xs与障碍Ωi的斥力,表达式为
(13)
式中:dob,i为平台Xs与障碍Ωi的距离;ρ为斥力作用距离;当Xs与Ωi的距离小于ρ时开始产生斥力,斥力作用距离应当取值为一定倍数的平台最小转弯半径以使平台能够规避障碍。通过以上方式构建的势场能够在Xg不在斥力作用范围内时,使Xg成为全局合力的最小值点。
对于引力Ua,显然有
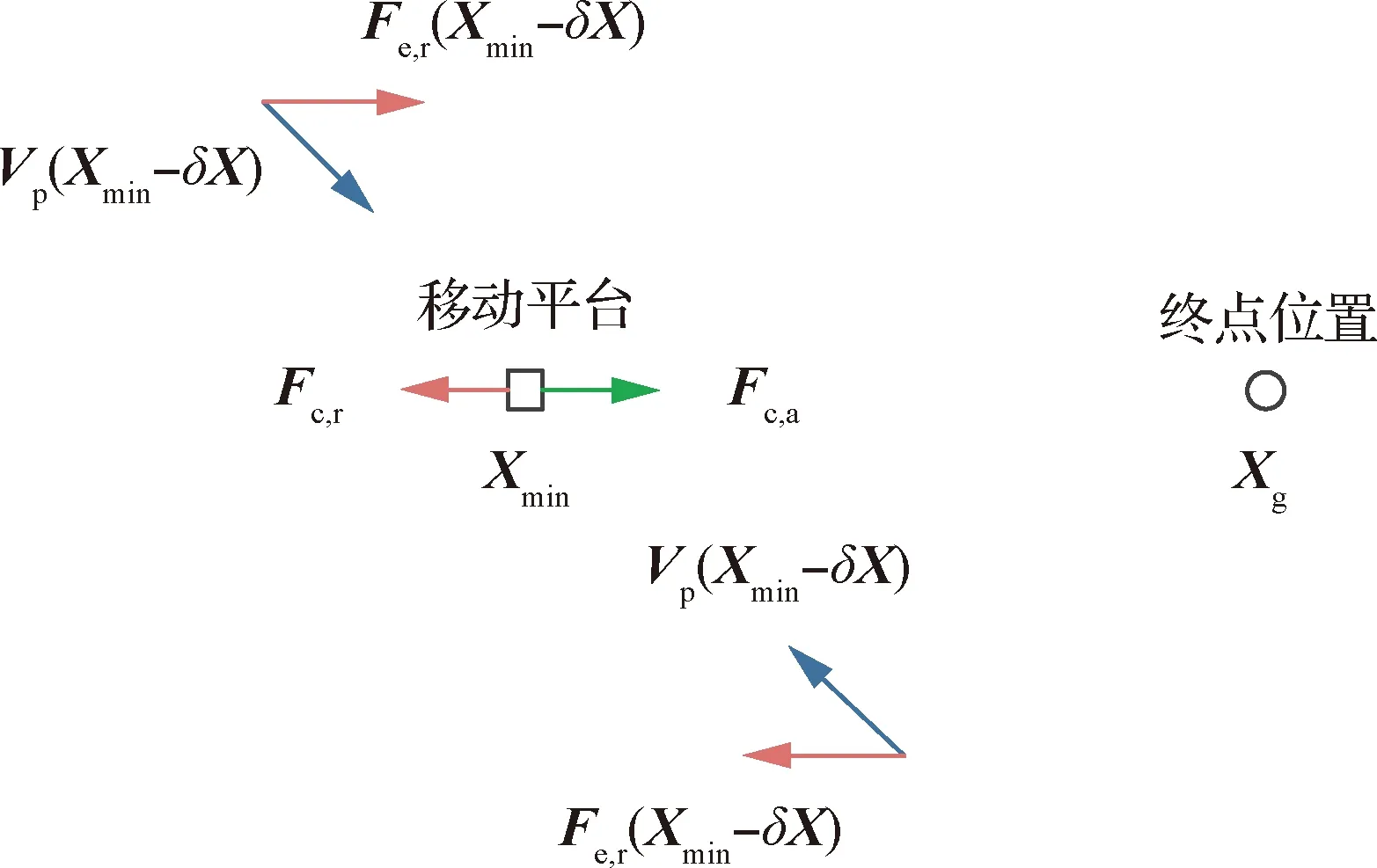
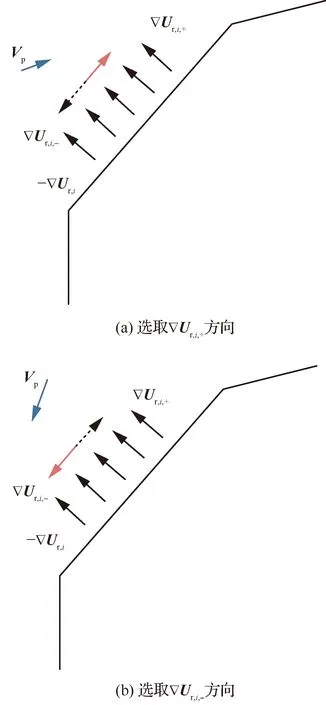
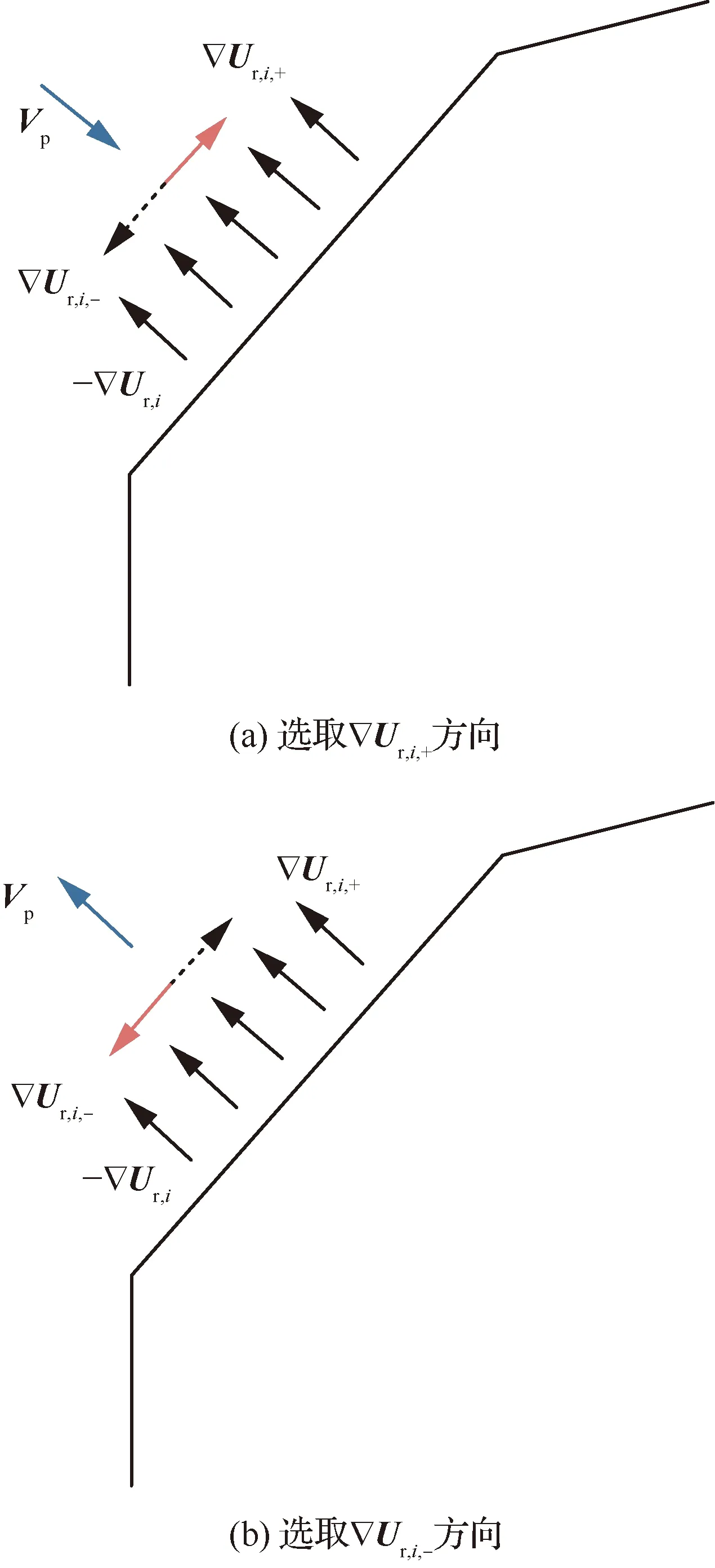
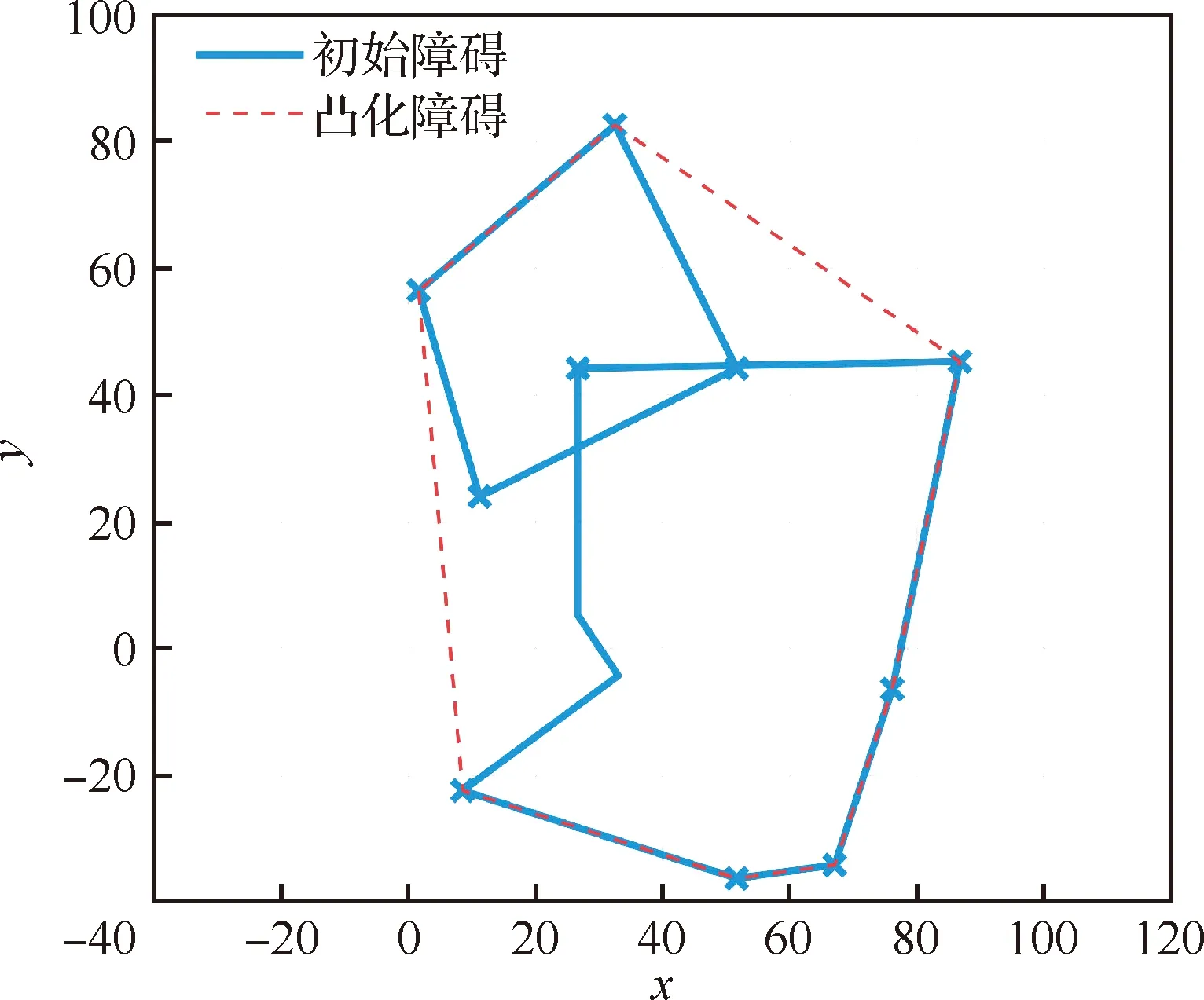
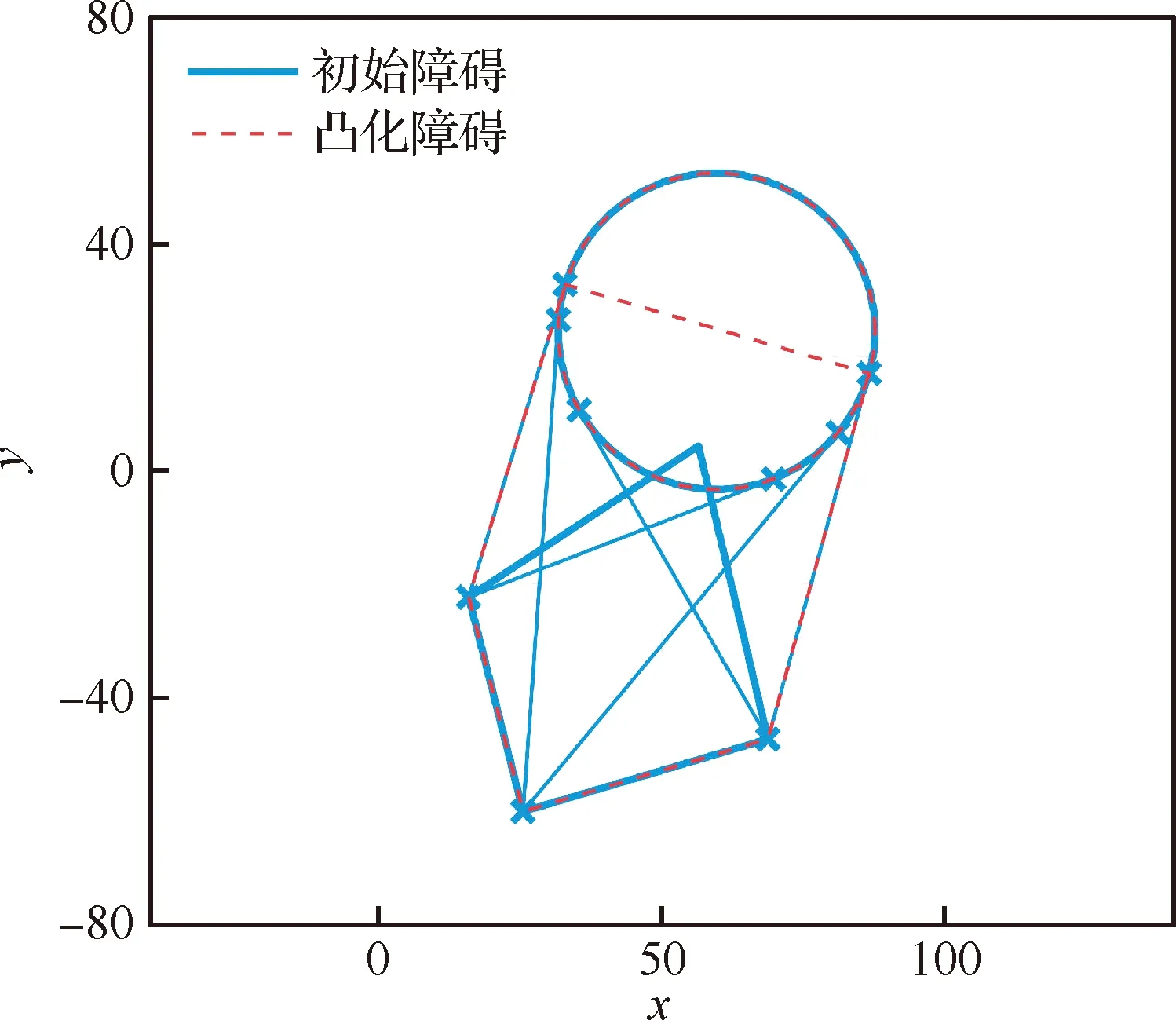
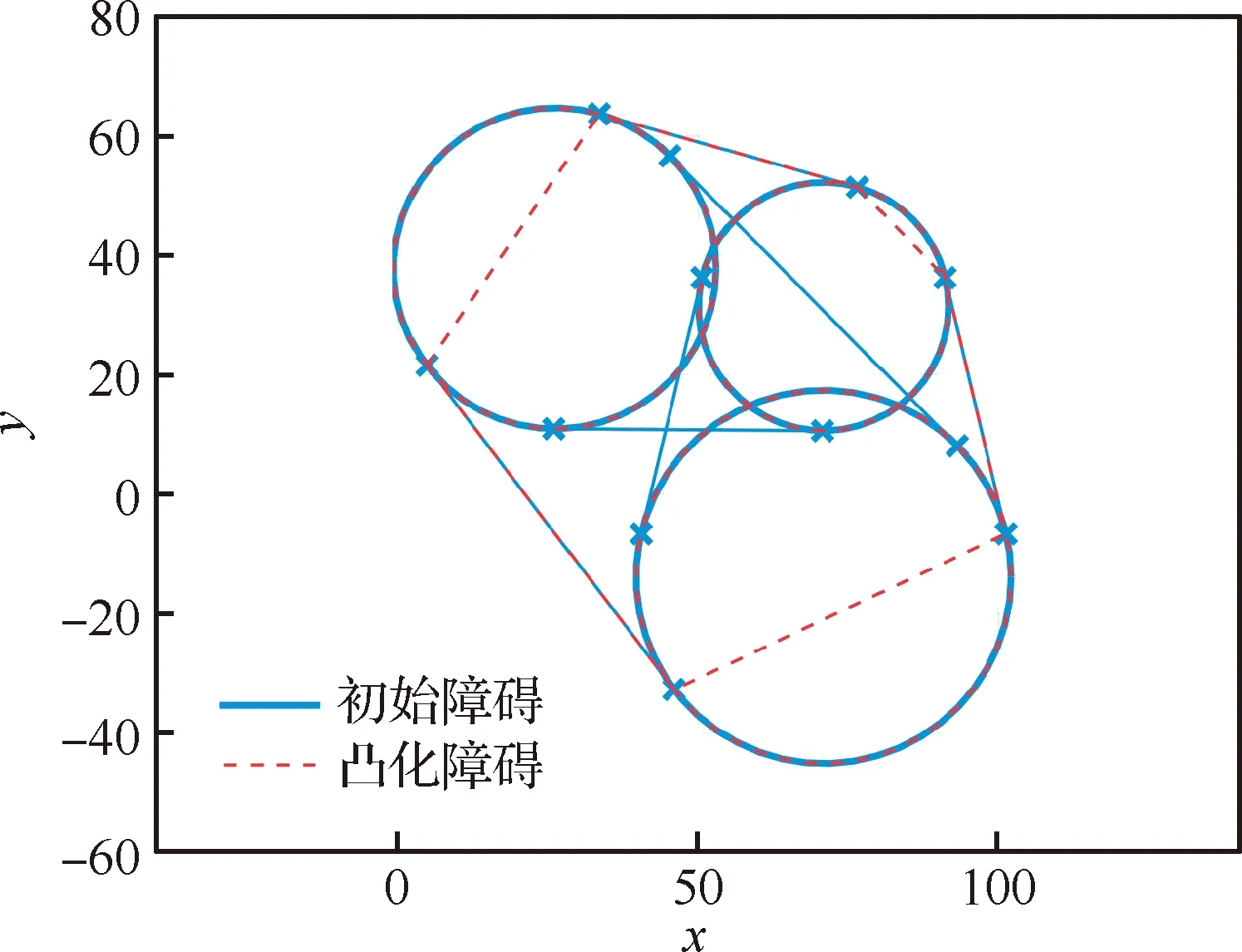
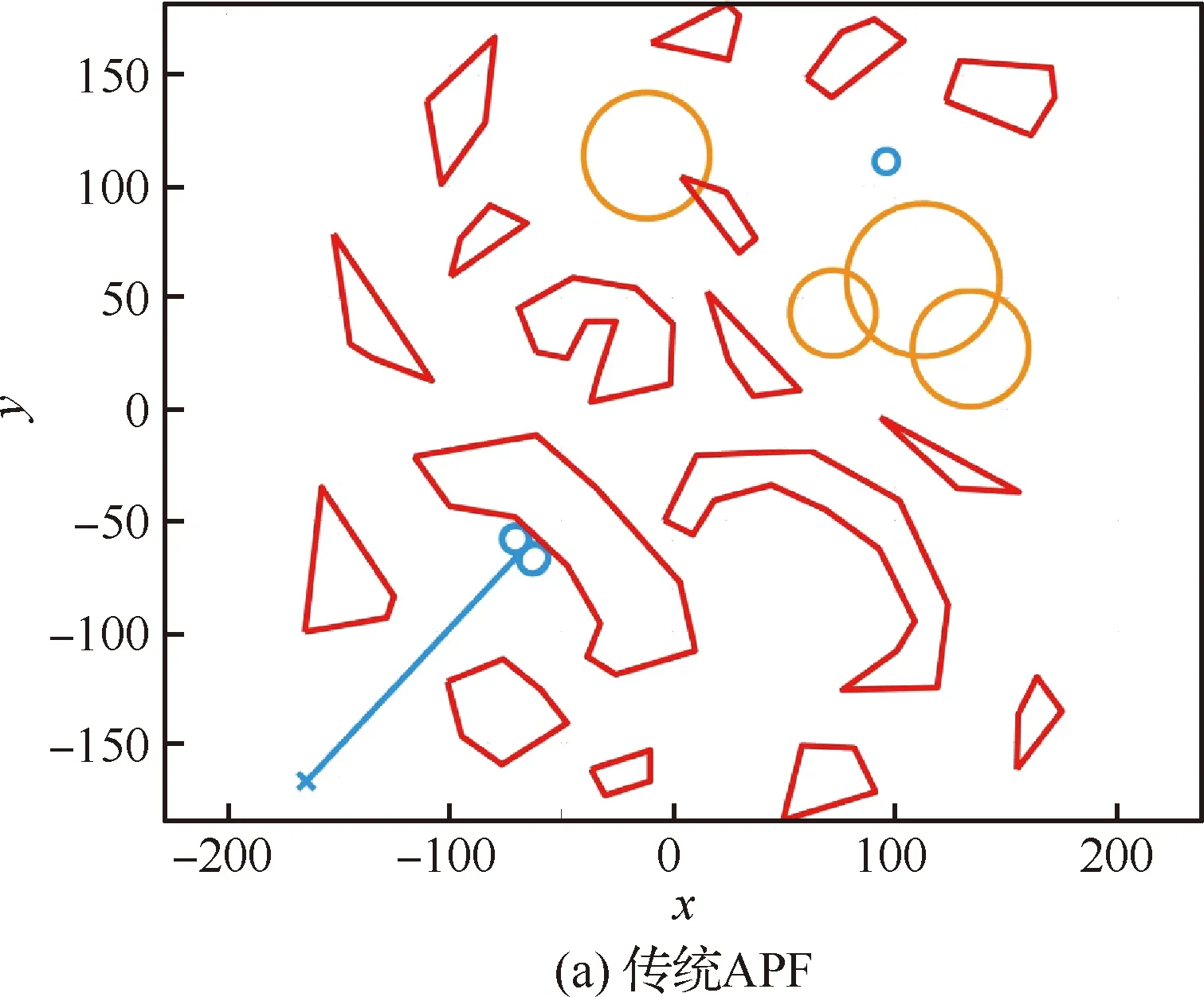
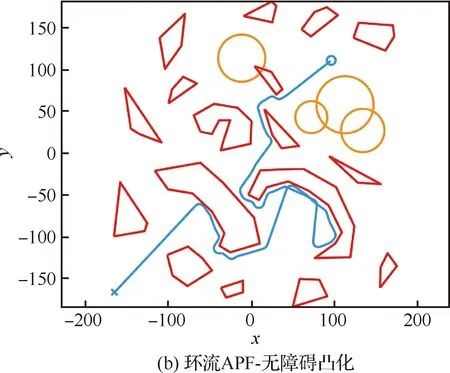
Ua(Xg)=0 (14) 对于斥力,显然有 (15) 从而,当Ur(Xg)=0,即Xg不在斥力作用范围内时,有 U(Xg)=Ua(Xg) (16) 即终点Xg是全局最小值点。 一般的APF方法假设障碍为点障碍,从而斥力Ur可以直接表示为障碍点Xob,i与平台当前位置Xs的函数,当障碍为凸多边形与圆形时,与点障碍类似,可以求解Xs到凸多边形或圆形的最近点作为障碍点计算斥力。 1) 凸多边形障碍最近距离点 设凸多边形障碍Ωop,i由有序顶点集合构成,记为{Xop,ij=[xop,ij,yop,ij]T},i为障碍序号。求解平台Xs与凸多边形障碍Ωop,i的距离,即求解Xs与Ωop,i中每条边距离的最小值。 以边Xop,ij到Xop,ij+1为例,设该边上的点Xτ,ij通过参数τ描述,即 Xτ,ij=Xop,ij+τ(Xop,ij+1-Xop,ij) (17) 式中:参数τ∈[0,1],从而Xs与Xτ,ij的距离为|Xs-Xτ,ij|,距离极值对应参数τ*为 (18) dop,ij= (19) 对应边Xop,ij到Xop,ij+1上的点Xdp,ij为 Xdp,ij= (20) 对于凸多边形障碍Ωop,i的所有边,依次求解dop,ij与Xdp,ij,取dop,ij的最小值作为Xs与Ωop,i的距离,记为dop,ij,对应Ωop,i边上的点记为Xdp,ij,之后即可直接采用点障碍的斥力模型进行斥力求解。 2) 圆形障碍最近距离点 圆形障碍记为Ωoc,i,圆心为Xoc,i,半径为roc,i,从而平台Xs与圆形障碍的最近距离doc,i为 doc,i=|Xs-Xoc,i|-roc,i (21) 对应Ωoc,i上的位置为Xdc,i (22) 在后文中,当不严格区分凸多边形障碍与圆形障碍时,Xs与障碍的最近距离与障碍上的对应点统一记为dob,i与Xd,i。 环流APF方法的引力势场记为Fc,a,斥力势场记为Fc,r,合势场记为Fc。环流APF方法的引力势场与传统方法相同,区别在于斥力势场。 (23) 环流斥力势场应当与平台原有的运动方向尽量一致,记平台航向方向单位向量为Vp=[cosβp,sinβp]T,则Fc,r,i为 Fc,r,i= (24) 图5 环流斥力势场方向的选取 另外,规定当Vp与-Ur,i方向相同时(朝向障碍边界且与障碍边界垂直),选取Ur,i,+作为环流斥力势场的方向;当Vp与-Ur,i方向相反时(远离障碍边界且与障碍边界垂直),选取Ur,i,-作为环流斥力势场的方向,如图6所示。 图6 环流斥力势场方向的选取(特殊情况) (25) 从而环流斥力势场和为Fc,r: (26) 合势场为 Fc=Fc,a+Fc,r (27) 由于环流斥力势场的方向与移动平台航向相关,因此在理论上能够克服传统APF方法的局部极小值问题,具体证明见附录A。 障碍凸化针对环境中出现的所有凹障碍以及障碍相交产生的凸区域。凸化过程分为2步:首先,进行障碍初始凸化,将环境中的所有凹多边形障碍凸化成为凸多边形障碍,从而使环境中只存在凸多边形障碍与圆形障碍;然后,进行相交障碍集合迭代凸化,判断环境中的障碍是否相交,将相交的障碍进行组合、凸化,消除相交障碍产生的凸区域。由于组合、凸化后的障碍会产生新的相交情况,因此还需要对于新得到的障碍再次进行相交判断与组合、凸化,即障碍集合迭代凸化。 对于凹多边形障碍Ωopc,i,顶点为{Xopc,ij=[xopc,ij,yopc,ij]T},通过如下步骤可以得到一个由Ωopc,i的顶点构成的凸多边形。 算法1多边形凸化 (28) (29) 4) 如果 (30) 则完成求解,得到的所有顶点(不包括第k+1个顶点)构成一个凸多边形,若不然,则跳转至步骤2)。 1) 多边形相交判断 多边形相交即判断两个多边形的边是否相交,以多边形ia与多边形ib的两条边Xop,iaja到Xop,iaja+1与Xop,ibjb到Xop,ibjb+1为例,若线性方程 (31) 的解τia与τib满足: (32) 式中: (33) 则说明交点位于两条边上,从而两多边形相交。分别对两个多边形的边进行相互判断,若均不相交,还需要判断两多边形是否为包含关系,即相互判断多边形ia中的一点(任取一顶点即可)是否为多边形ib的内点,内点判断可以直接采用内角和判断方法,若ib相邻顶点与ia中一点的夹角和为2π,则该点是内点,两多边形为包含关系,相交。 2) 多边形与圆形相交判断 多边形与圆形相交判断即判断多边形的每条边与圆心的距离是否小于等于圆的半径,圆心与多边形边的距离计算模型可以使用式。 3) 圆形相交判断 圆形相交判断即判断两圆心的距离是否小于等于两圆的半径和。 彼此相交的障碍构成一个相交障碍的集合,在这个集合中,对于任意一个障碍,均存在另一个障碍与该障碍相交,而并非要求集合内的任意两个障碍均相交。如图7所示,图7中C-A与C-B相交,C-B与C-C相交,C-A与C-C不相交,但是C-A,C-B,C-C构成一个相交障碍的集合,这是因为若至针对C-A与C-B进行相交障碍凸化,则凸化后的图形仍然会与C-C产生一个凹区域。 图7 相交障碍集合 与图7中的情况类似,首先将所有障碍分成若干个相交障碍集合Ψγ={Ωi},其中γ为序号,对于集合Ψγ中的任意一个障碍Ωi,均存在另一个障碍Ωi*∈Ψγ与Ωi相交。若某一个障碍不与任何其他障碍相交,则无需凸化,因而不属于Ψγ。 对于Ψγ,需要求解其中任意两个障碍的特征点(这两个障碍可能不相交),以构成一个能够包含Ψγ中所有障碍的凸多边形。 不同障碍间的特征点与凸化结果如图8~图10所示,特征点为蓝色“×”,凸多边形由这些特征点通过算法1得到。 1) 多边形的特征点 多边形相交的特征点为两个多边形所有顶点的并集,如图8所示。 2) 多边形与圆形的特征点 多边形与圆形的特征点为多边形所有顶点,以及所有多边形顶点(不包括圆形内部的顶点)与圆形的切点构成的并集,如图9所示,圆形外点与圆的切点求解不再赘述。 3) 圆形的特征点 圆形的特征点为两个圆的公切点(公切线不相交),如图10所示,公切线求解方法在此不再赘述。 得到集合Ψγ内任意两障碍的特征点后,构成一个所有特征点的集合,采用算法1凸化成为一个凸多边形,该凸多边形与集合Ψγ内所有圆构成覆盖集合Ψγ内所有障碍的凸图形,并作为相交障碍凸化结果。 图8 多边形的特征点 图9 多边形与圆形的特征点 图10 圆形的特征点 经过相交障碍凸化,得到的结果可以分为3部分:① 所有不与其他障碍相交的障碍;② 相交障碍集合构成的凸多边形;③ 相交障碍集合内的圆。 由于产生的新凸多边形可能与已有障碍相交而产生凹区域,因此还需要对结果进行障碍相交判断与相交障碍凸化,即障碍集合的迭代凸化,当前后两次的结果一致时,迭代结束,得到的所有障碍作为凸化的障碍用于路径规划。 为验证方法有效性,首先在复杂障碍场景下与现有方法进行路径规划求解对比;之后在不同数量障碍的场景下分析方法的运算耗时。 分别采用不同的APF方法求解不同场景下的路径规划。方法包括传统APF方法,环流APF方法(不使用障碍凸化),环流APF方法(使用障碍凸化)。在仿真分析过程中,将所有长度去量纲化处理,设定平台的最小转弯半径为3,平台速度为3/s,计算时间步长为0.3 s,斥力作用距离为9。两种场景设定为 场景A21个障碍,其中,4个圆形障碍,3个凹多边形障碍,14个凸多边形障碍。 场景B53个障碍,其中,15个圆形障碍,4个凹多边形障碍,34个凸多边形障碍。 不同APF方法得到的路径规划结果如图11和图12所示,两种场景下的障碍凸化结果如图13和图14所示。 图11 场景A路径规划结果 图12 场景B路径规划结果 图13 障碍凸化-场景A 图14 障碍凸化-场景B 根据结果可得: 在两种场景下,由于在路径初始阶段设置了一个凹多边形的障碍,且凹陷部分正对平台航向,传统APF陷入了势场的局部最小值而无解,虽然已经对合势场为0时的情况进行预先设置了规则,即当合势场为0时进行90°的转向,但是这种简单的策略并没有改善传统APF的效果。 相比之下,环流APF方法在场景A中虽然有解,但是路径的一部分在凹多边形障碍中出现了绕行,而在场景B中环流APF方法无解。虽然环流APF方法通过改变传统斥力势场的方向使平台能够贴着障碍边界运动,但是当平台进入凹多边形凹陷部分时,可能一直在凹多边形凹陷部分内绕行甚至进入障碍(见图15)而依然无解。可见,如果不对障碍进行凸化,环流APF能否有解将取决于障碍凹陷的程度,环流APF能够逃离较浅的凹多边形,但是却有极大的可能陷入较深的凹多边形内。另外,注意到图15中平台进入了障碍,这是由于凹区域与平台的距离极值点不唯一,距离计算错误地选择了不应该产生斥力的边。 相应地,在对障碍进行凸化后,环流APF能够给出较为合理的路径规划结果。 基于障碍凸化的改进APF方法主要分为两个过程,一是障碍凸化,二是路径规划。障碍凸化需要一次计算完成,而路径规划可以在每个时间步长内单独计算。 在不同障碍数量条件下分析方法的计算耗时,目标位置与平台初始状态保持一致,改变障碍数量,不同场景的障碍数量如表1所示。 表1 不同场景的障碍数量 在不同障碍数量的场景下进行路径规划,得到的路径规划结果如图15所示。 图15 不同障碍数量场景下的路径规划结果 不同障碍数量场景下的路径规划单步计算耗时如图16所示,平均单步计算耗时、平均单步耗时/障碍数量、障碍凸化耗时如表2所示。 图16 单步计算耗时 表2 计算耗时 根据表2结果可得:障碍凸化耗时与障碍数量、障碍复杂程度有直接的相关性,并且随着障碍数量与障碍复杂程度的提升,障碍凸化耗时的增加并不是线性的。在场景C-3与C-4中,由于存在相交障碍,因此障碍凸化耗时相比C-1与C-2显著增加,这是由于障碍集合迭代凸化过程耗时较长,但是总体耗时仍然在可以接受的程度之内(C-4场景82个障碍,耗时1 786.111 ms)。另外,虽然C-1中的障碍数量少于C-2,但是障碍凸化耗时与平均单步耗时长于C-2,这是由于C-1中的多边形数量多于C-2,多边形的初始凸化、相交判断、斥力计算相比圆形的耗时更长。 在单步耗时方面,所有场景的单步耗时均在ms级,并且平均单步耗时与障碍数量的比值趋同,对于每一个障碍,计算耗时约为0.02~0.03 ms。可以以此为根据设定计算的时间步长,使在每个时间步长内均可以保证完成路径规划求解。 计算环境为i7-7700T@2.90 GHz,8 GB RAM,Windows 7 x64,MATLAB 2018a。 在可行性方面,改进方法相比传统APF方法或不采用障碍凸化的环流APF方法,能够明显提高复杂障碍环境下的APF路径规划求解可行性。 在计算耗时方面,方法的计算耗时主要分为障碍凸化耗时与路径规划单步计算耗时2部分。障碍凸化耗时主要与障碍数量、障碍复杂程度相关,仿真环境下,在障碍数量82,相交障碍数量为42时,障碍凸化耗时约为1 786.111 ms;单步计算耗时与障碍数量密切相关,并且呈近似线性关系,每个障碍所需的单步计算耗时约为0.02~0.03 ms,可以以此为基准设定时间步长,以保证每个时间步长均能够完成路径规划计算,进而支持在线的APF方法路径规划。 附录A 为便于理论分析,引入理想移动平台的概念,理想移动平台总能沿着势场方向运动,即最大角速度与角加速度趋于∞。环流APF方法能够保证理想移动平台航路规划有解,即理想移动平台采用环流APF方法,总能抵达终点。 值得注意的是,限定障碍为凸障碍的目的是使对于每个障碍而言,平台与障碍之间的距离最小值点有且只有一个。而在凹障碍中,当平台处与障碍凹陷部分时,可能会出现多个平台与障碍的距离最小值点。从而无法定义障碍对于平台的斥力。 定理A1在凸障碍环境中,环流APF方法的势场不存在局部极小值 证明: 采用反证法,设凸障碍环境中,环流APF方法的势场存在局部极小值点,即对于Xmin≠Xg,有 Fc(Xmin)≡0=Fc,r+Fc,a (A1) 此时,引力势场Fc,a与斥力势场Fc,r的分布如图A1所示。 图A1 合势场为0的情况 设Vp(X)是指向Xmin处的单位向量。由于Xmin是局部极小值,因此存在Xmin的去心邻域,该去心邻域内的所有位置势场均指向Xmin。因而也存在位置微元δX,Vp(Xmin+δX)与Vp(Xmin-δX)均指向Xmin,由于Vp是单位向量,因此有 Vp(Xmin+δX)=-Vp(Xmin-δX) (A2) 注意到环流APF方法斥力势场的方向定义,当平台分别处于Xmin+δX与Xmin-δX位置并且航向指向Xmin时,平台航向相反,环流斥力势场的方向也相反,即 (A3) 如图A2所示。 图A2 斥力势场相反的情况 Fig.A2 Situation that repulsive potential fields are opposite 因此,平台分别以航向Vp(Xmin+δX)与Vp(Xmin-δX)经过Xmin时,有 Fc,r[Xmin|Vp(Xmin+δX)]= -Fc,r[Xmin|Vp(Xmin-δX)] (A4) 从而平台分别以航向Vp(Xmin+δX)与Vp(Xmin-δX)经过Xmin时,若存在 Fc[Xmin|Vp(Xmin+δX)]=0 (A5) 则必有 Fc[Xmin|Vp(Xmin-δX)]=0= -Fc,r[Xmin|Vp(Xmin+δX)]+Fc,a= 2Fc,a≠0 (A6) 其中,由于Xmin不是终点,因而Fc,a≠0,与假设矛盾。因此Xmin不是局部极小值点。 另外,当理想移动平台以航向Vp(Xmin+δX)经过Xmin时,若有合势场 Fc[Xmin|Vp(Xmin+δX)]=0 (A7) 且Fc(Xmin+δX)指向Xmin,移动平台将会被“拉回”Xmin并且航向会被反转,当移动平台以航向Vp(Xmin-δX)再次经过Xmin时,则有 Fc[Xmin|Vp(Xmin-δX)]=2Fc,a(Xmin) (A8) 从而斥力势场Fc,r[Xmin|Vp(Xmin-δX)]与引力势场Fc,a(Xmin)相同,合力势场将引导移动平台离开Xmin位置并且不再返回。但是对于终点位置Xg,由于Fc,a(Xg)=0,从不同方向进入Xg的合势场是可以相等且为0的。 根据以上分析,由于环流APF方法的斥力势场构建方式与移动平台航向相关,对于同一个位置,若移动平台的航向相反,则斥力方向也相反,因而环流APF方法对应合势场为0的位置,并不会表现为一个传统的局部极小值点使移动平台陷入该点,当移动平台再次从相反的方向经过该位置时,该位置的势场将不再为0而是与引力方向相同使移动平台向终点位置移动。 定理A1仅说明对于理想移动平台,环流APF方法能够保证有解,对于实际的移动平台,其角速度与角加速度是受限的,因此实际中仍然可能出现无解的情况。2.4 凸多边形与圆形障碍的斥力描述
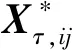
2.5 环流APF势场

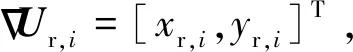

3 障碍凸化
3.1 障碍初始凸化
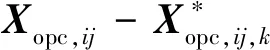
3.2 障碍相交判断
3.3 相交障碍凸化

3.4 相交障碍集合迭代凸化
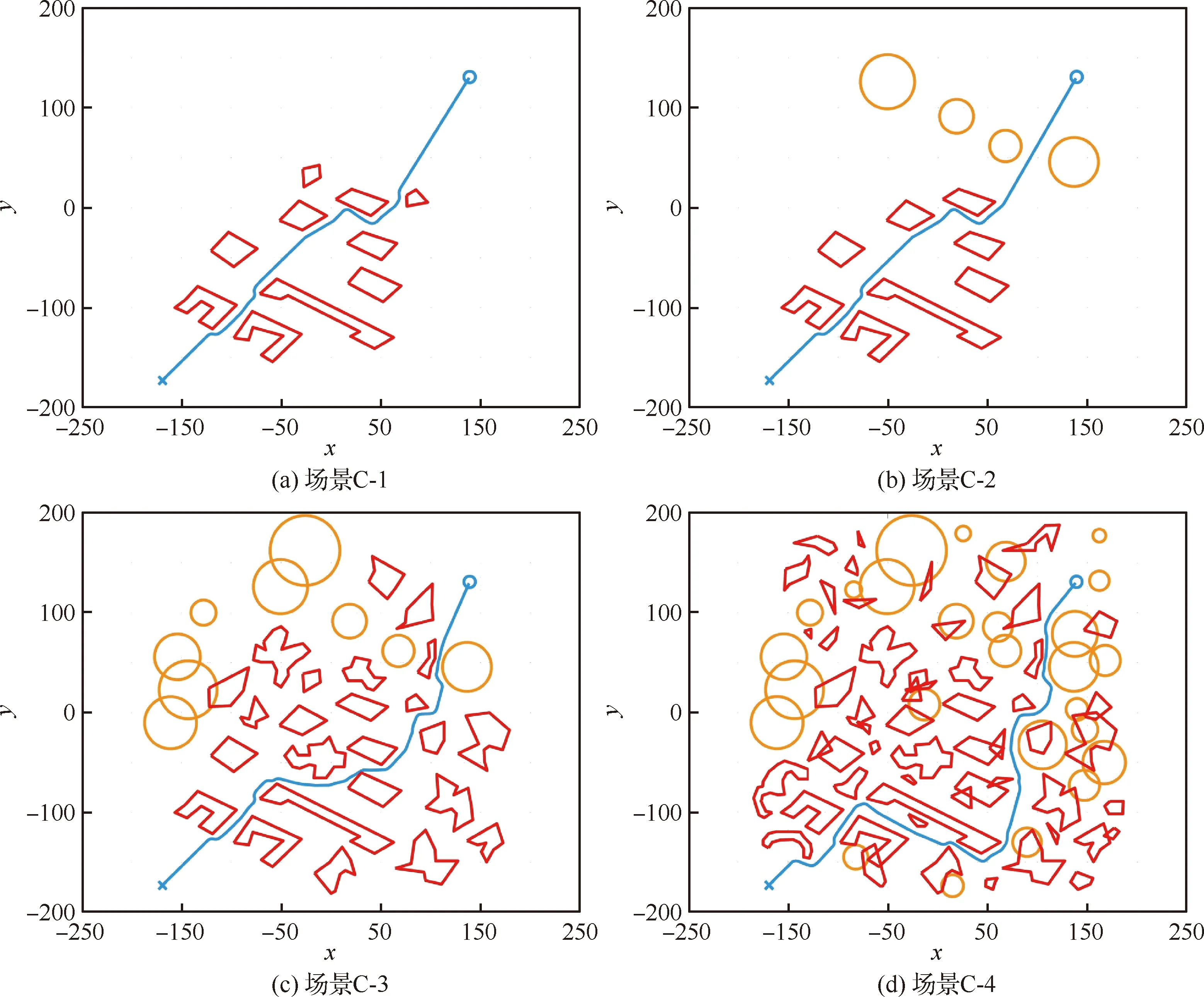
4 仿真分析
4.1 复杂障碍场景下的求解对比
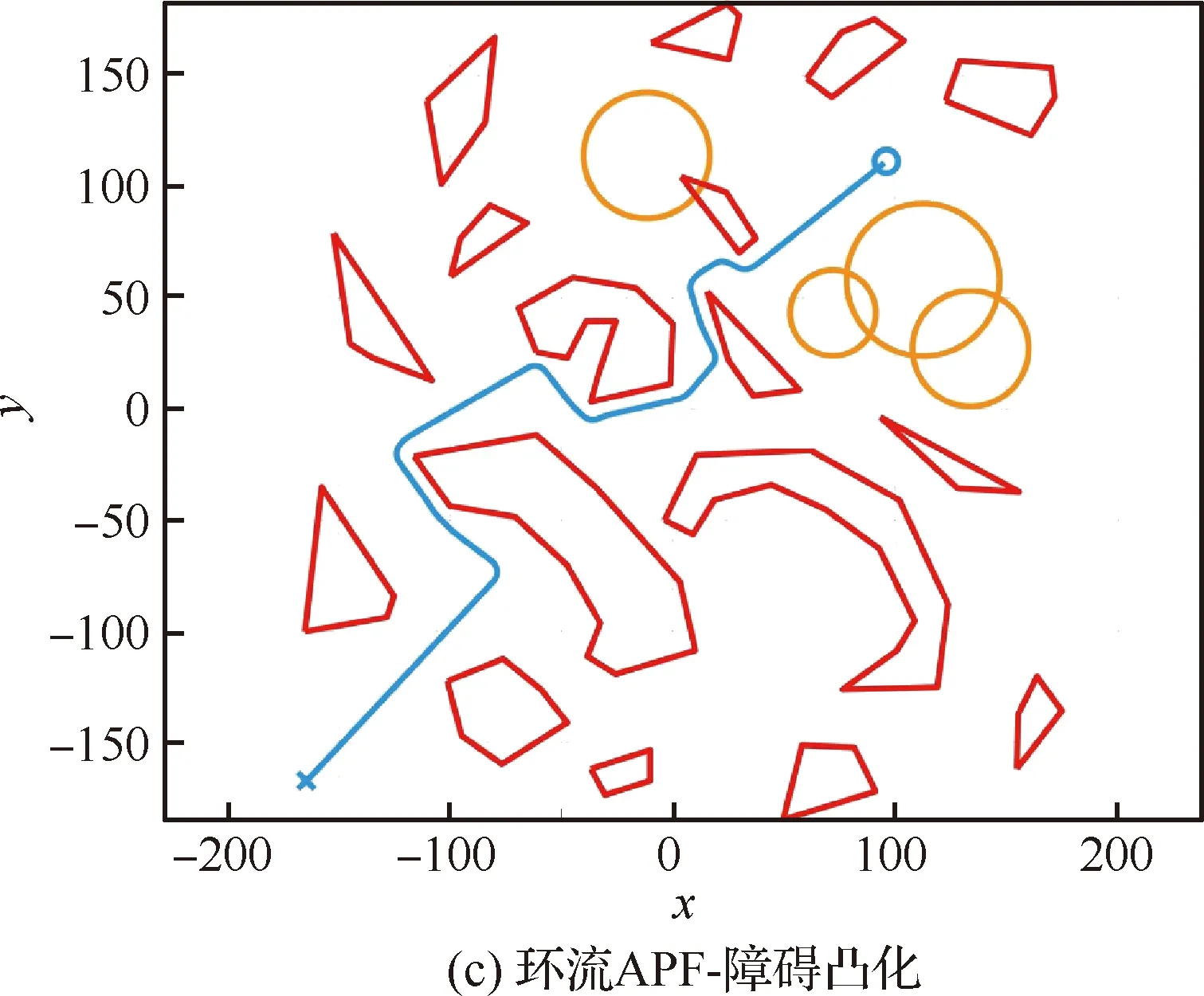
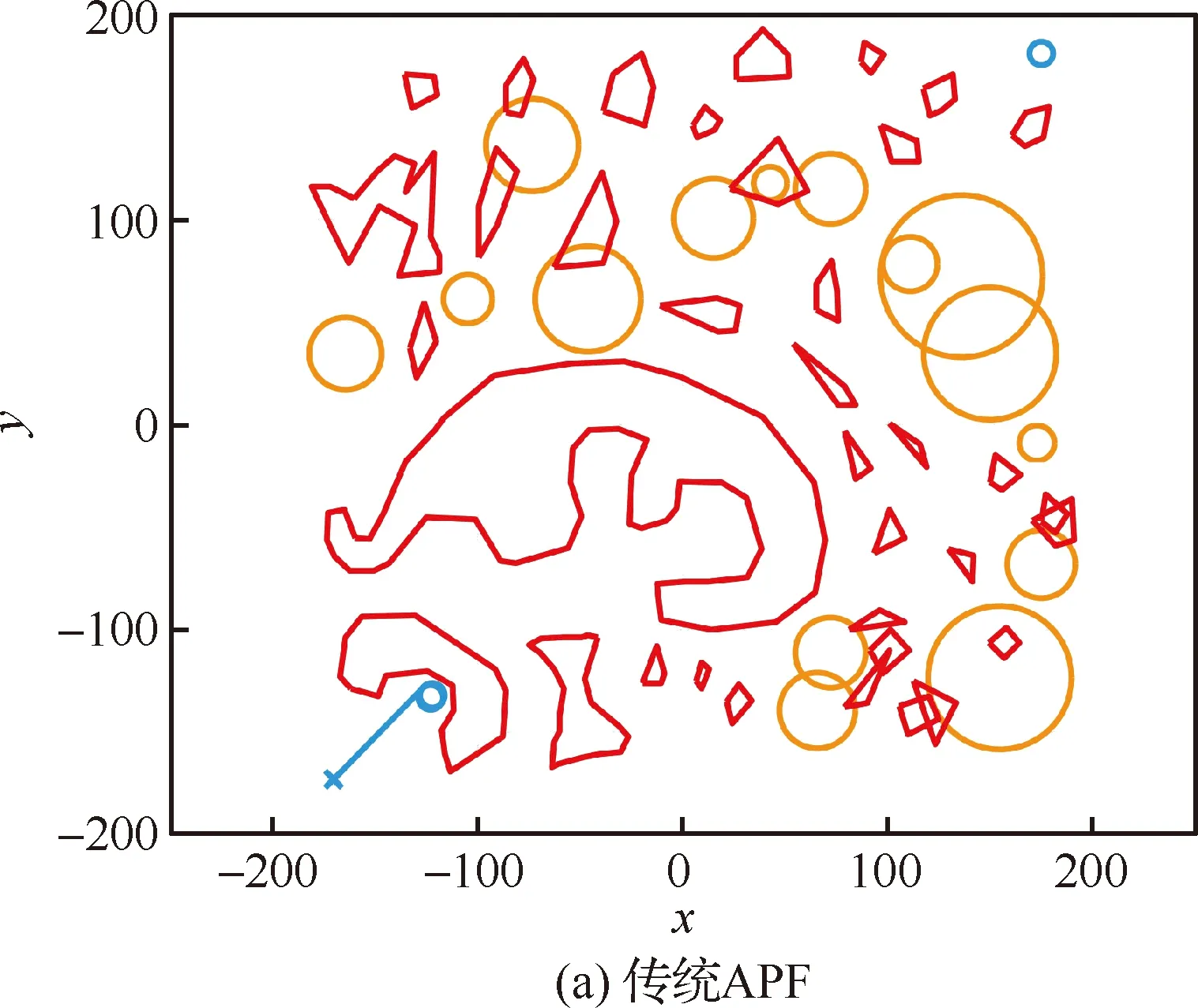
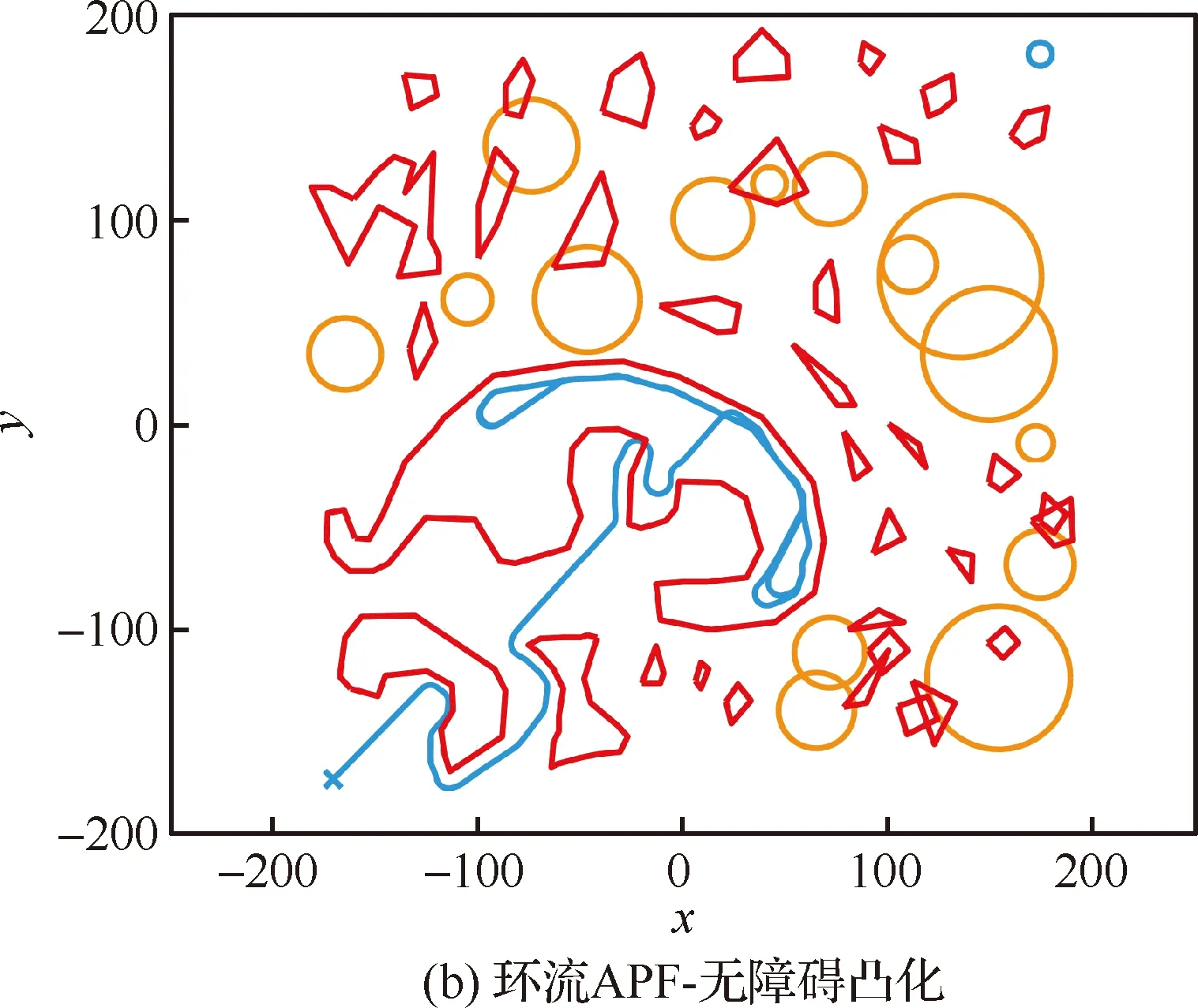



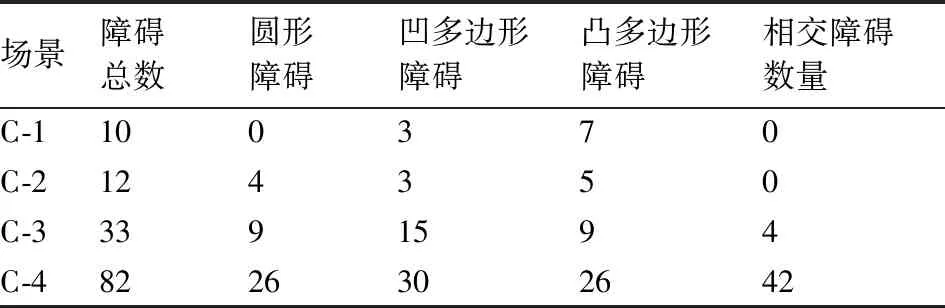
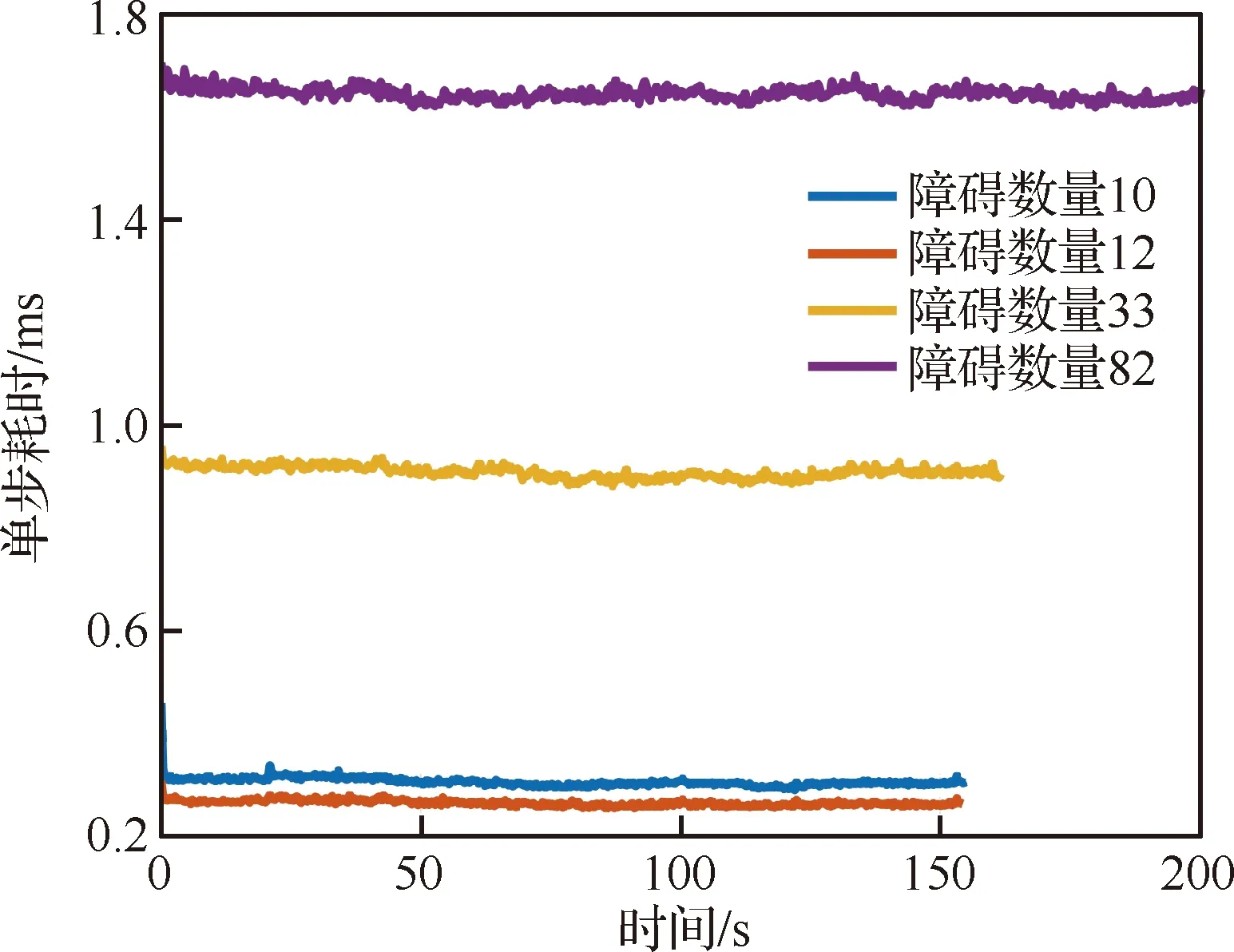
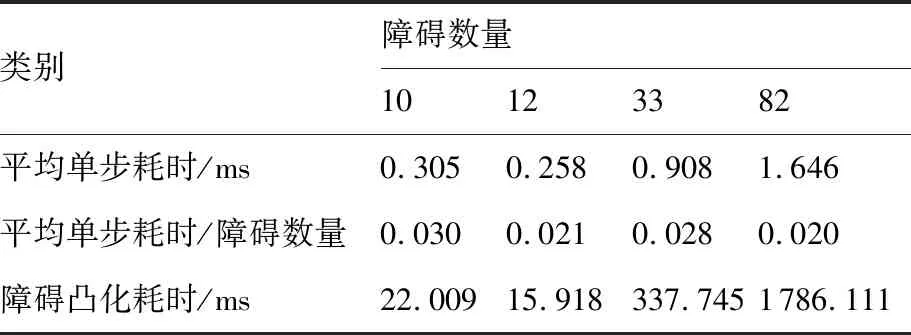
4.2 方法计算耗时分析
5 结 论