楔形体入波浪水面数值模拟

金禹彤，陈吉昌，卢昱锦，肖天航，童明波

南京航空航天大学 航空学院 飞行器先进设计技术国防重点学科实验室，南京 210016

随着海洋资源的不断开发和建设，波浪因其具有较高的能量密度及对飞行器水上迫降、起降和滑行性能有重要影响而备受关注[1]。飞机着水是指飞行器为完成巡逻、反潜和救援等任务时，在正常操作程序中降落于水面的航态。其降落着水过程中，机体承受着较为严重的水动冲击载荷[2]。即使是相对温和的海况也会对飞行器造成临界载荷和无法控制的运动。在完成波浪条件降落着水任务的同时，保证机体内部人员的生命安全，对机体结构强度提出了更高要求。因此，进一步掌握飞行器波浪水面降落性能及水体对机身的载荷作用，对飞行器入波浪水面的技术研究和工程应用具有重要意义。

使用物理水池模型试验对结构物水动力性能进行研究和预报始于20世纪中期，该方法为验证理论和数值预报方法的有效性提供了检验标准，如荷兰的瓦格宁水池、美国著名的船舶耐波性试验水池——泰勒水池(David Taylor Model Basin, DTMB)[3-6]和挪威海洋工程技术研究院(MARINTEK)的海洋工程水池[7]等。但物理水池的建造和维护需要大量的资金、设备、场地和人员投入；而且，物理水池模型试验还受水池大小的限制，模拟试验结果存在比尺效应，试验结果还会受到试验探测仪器精密度、探测方法等诸多因素的影响。考虑物理水池试验的局限性和经济性，随着数值仿真技术的成熟，构造数值水池已经成为研究物体入水冲击过程的重要方法。

目前构造数值波浪水池的方法主要有源项造波法、推摇板造波法和速度入口造波法。Brorsen和Larsen[8]使用源项造波法完成对二维任意类型波浪的模拟。李胜忠[9]同样采用源项造波法，完成对线性规则波和Stokes波等波浪的数值模拟。但对于复杂的黏性流动问题，源项表达式不易推导，不能快速有效地完成数值波浪水池的构造。储慧林[10]、王文华[11]和王平[12]等基于CFD数值方法，结合推板造波和海绵阻尼消波原理实现数值造消波，分别研究鱼雷、圆柱和楔形体入规则波波面过程，但该数值造波方法网格量较大，产生过高的计算成本。Longuet和Cokelet[13]最先使用速度入口造波法生成规则波，且结果与Stokes理论解吻合较好。Boo[14]通过对线性规则波和不规则波仿真，验证了速度入口造波法的有效性，进一步研究线性和非线性不规则波在垂直圆柱上的作用力。从基本物理模型的实用性、计算精度和计算成本等方面考虑，速度入口造波法更为合理可靠，且已在结构物波浪水面滑行问题上[15-16]得到广泛应用。

陈宇翔等[17-18]采用有限体积法模拟圆柱出/入水过程，用动态铺层法处理模型与水面的相对运动，对出/入水过程的水面变化捕捉较好。但其弊端是只考虑圆柱的一自由度运动，而忽略圆柱的偏转运动。Abraham等[19]运用动态网格重构法数值模拟球体入水过程，对球形体附近网格加密，通过网格的变形和重构实现对球形体下落过程的模拟，但该动网格方法产生过高的计算成本。Wick等[20]采用有限体积法求解非定常Navier-Stokes方程，结合流体体积模型(Volume of Fluid, VOF)液面捕捉技术和动网格方法，对某型无人机(Unmanned Air Vehicle, UAV)不同高度的入水冲击过程进行了数值模拟。Wick采用的动网格方法是将计算域划分成两部分，一部分是包裹UAV的球形体(子域)，该部分网格采用六面体结构，并随着UAV的运动而运动，且子域内的网格不发生变形；另一部分是球形体以外的其他计算域网格(外子域)，该部分网格采用四面体结构，通过网格重构模拟UAV溅落过程。Guo等[21]采用同样的数值求解方法和动网格技术，研究俯仰角对某型运输机水上迫降特性的影响。Carrica等[6]采用的动网格方法产生的计算成本过大，且计算精度不高。Qu等[22]运用整体运动网格法处理模型与水体的相互作用，对结构物水上迫降性能进行数值模拟。该动网格方法中，整个计算域(包含网格单元和边界条件)随着模型的运动而运动，而无需划分子域和外子域。结果表明，整体运动网格法可以精确捕捉自由液面，有效避免计算量大、网格质量差等问题。卢昱锦等[23]采用有限体积法和整体动网格法对高速平板着水问题进行数值仿真，研究不同俯仰角对空气泡现象的影响规律。

基于此，本文以FLUENT软件为数值模拟求解器，采用结合整体动网格法的速度入口造波方法及VOF液面捕捉技术，在构造线性规则波和线性不规则波数值水池的基础上，耦合三自由度模型，数值模拟楔形体入波浪水面过程，分析规则波波形位置对楔形体受力特性和运动姿态变化的影响，并初步探索二维楔形体入不规则波及三维楔形体入规则波情况，为飞行器波浪水面起降和滑行问题的研究提供参考和技术支持。

1 数值计算方法

1.1 流体方程及求解

流体控制方程为非定常不可压缩流动雷诺平均Navier-Stokes(URANS)方程和剪切应力输运(SST)k-ω湍流模型，水气交界面采用VOF模型进行捕捉。求解器采用压力基求解器、非稳态时间格式，压力-速度项采用PISO(Pressure Implicit with Spltting of Operators)算法进行迭代计算，采用有限体积法离散控制方程：压力差值格式采用PRESEO格式，其余项均选用二阶迎风格式。

1.2 速度入口造波与源项消波

速度入口造波法是给定入口边界处的波浪位置和水质点速度，随着时间步的迭代，波浪在入口边界处生成，并逐渐传播到计算域内。对于线性规则波，即为常深度二维小振幅推进波，其波面高度η(x,t)相对于坐标x或相对于时间t作周期性的变化，并且波形以一定速度c沿x向传播。波浪参数及波形位置说明如图1所示。

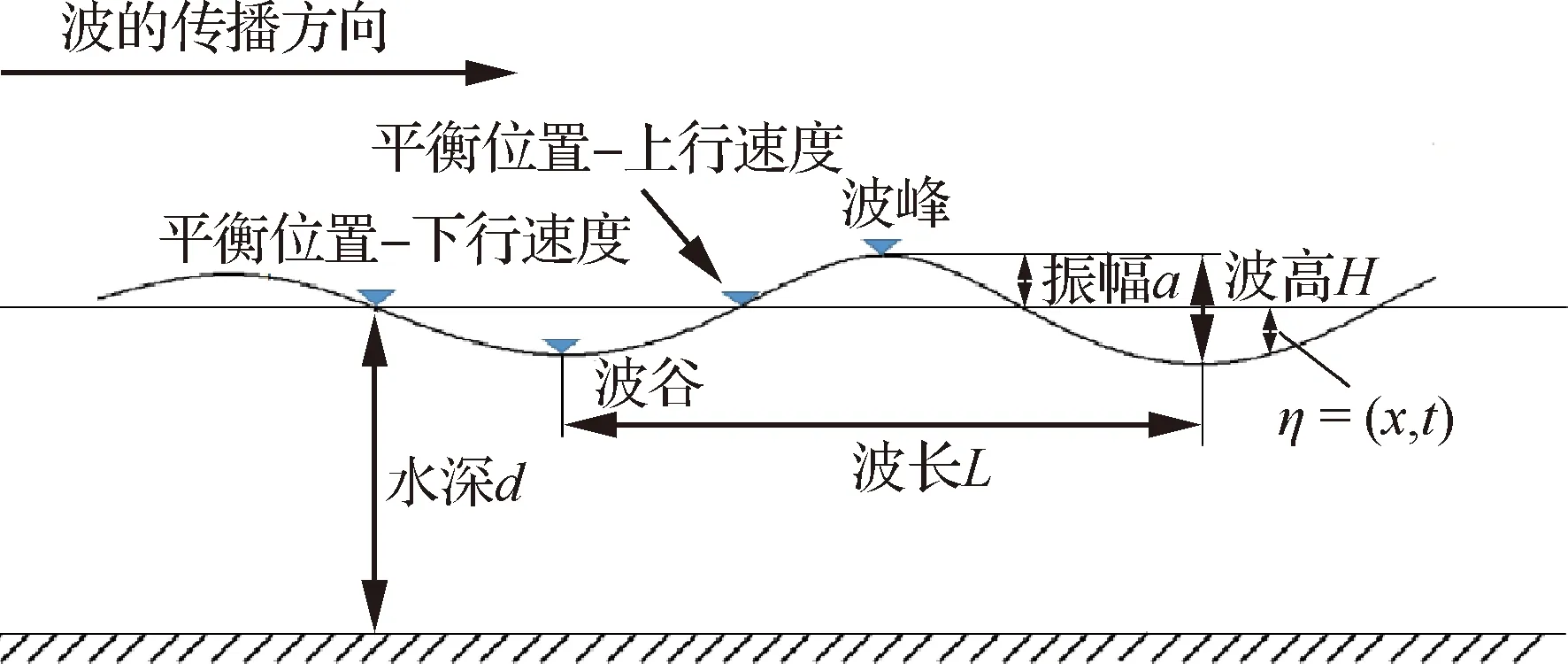
图1 波浪参数及波形位置

设常深度二维小振幅推进波的波面方程η(x,t)为

(1)

式中：H为波高；k为波数；ω为圆频率。

波浪中水质点(x,y)的速度分量u、v的表达式为

(2)

式中：φ为速度势函数；T为周期；d为水深。

对于线性不规则波，采用Longuet-Higgins提出的线性叠加海浪模型，将随机海浪这种平稳随机过程描述为由无限多不同周期、振幅和不同随机初相位，并且在xoy平面上与x轴成θ度方向角的斜向余弦波叠加而成的波列，单向线性不规则波中θ=0°。单向线性不规则波波面方程及波浪中水质点(x,y)的速度分量Vx、Vy的表达式为

(3)

式中：Hi为单个组成波的波高；Ti为单个组成波的周期；ki为单个组成波的波数；ωi为单个组成波的圆频率；ai为单个组成波的振幅；εi为单个组成波的初相位。

阻尼消波法采用动量源项消波方式，即在动量方程中增加一个动量衰减的源项，源项表达式[24]为

(4)

式中：x≠x0表示计算域在造波区；x=x0表示在消波区。

1.3 整体动网格法

整体动网格法是指包括网格单元和边界在内的整个计算域与模型有相同的运动规律，即随着模型的运动而运动[22-23]。

整体动网格方法不需考虑弹性变形和网格重构，提高计算效率和精准度的同时，可以有效地处理复杂几何构型、边界条件和水气液面捕捉。在整体动网格法中，采用体积分数边界条件以保证水平面保持在初始高度。该边界条件是基于欧拉坐标系网格点的高度设定，空气体积分数αa=0.5表示该网格位于水气交界面，αa=1.0表示该网格位于水面以上，αa=0表示该网格位于水面以下，体积分数分布如图2所示。

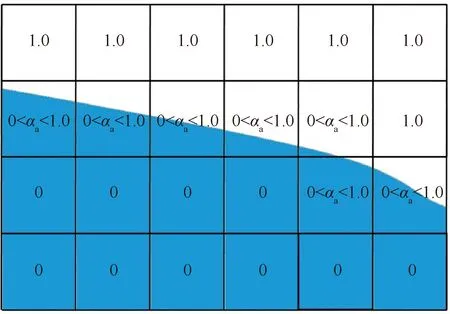
图2 空气体积分数

2 算例验证

2.1 数值造波及波形验证

本节数值验证速度入口造波法和源项消波法的有效性和准确性。波浪参数[25]为：波高H=0.08 m，水深d=0.5 m，周期T=1.25 s，波长L=2.181 m。

由于自由液面区域附近的物理量梯度变化大，则将自由液面加密区域延伸到0.3 m(± 0.15 m上下平均水面)；此外，为了减小由于垂向和纵向网格尺寸的突变而对数值扩散和阻尼消波的影响，实现网格的平滑过渡，取计算域网格的偏差增长率为1.2。网格参数见表1所示，计算域及边界条件设置见图3。用相同的波浪参数、计算域、网格尺寸和加密方式生成并验证不规则波。

计算输出规则波波形在x=-6.5，-3，0，3，11 m处的数值解，并与理论解析解对比，如图4所示。数值解波形向上偏移1%，主要考虑湍流模型的影响；且在x=11 m处数值解波形被吸收，说明阻尼消波法有效，不规则波数值解和理论解析解基本吻合(见图5)。

图6给出计算域内规则波和不规则波波形和流场分布。综上，速度入口造波法和阻尼消波法有效且准确。

表1 网格参数

图3 波浪水面计算域及边界条件

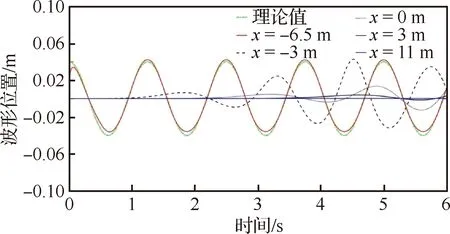
图4 规则波波形对比

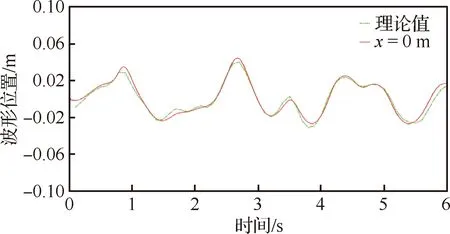
图5 不规则波波形对比

图6 波形及流场分布

2.2 楔形体静水面入水

数值模拟楔形体在静水面的入水过程，并与试验结果[26]和理论解[27-29]对比，验证数值方法及整体动网格法模拟物体入水过程的准确性和可行性。楔形体模型[26]的横截面如图7所示。

采用结构化网格，整体计算域长和宽均为5 m，其最小网格尺寸在楔形体处为0.005 m，最大网格尺寸在边界处为0.06 m，计算域网格结构及计算模型初始时刻如图8所示。初始时刻，楔形体位于静止水面上方且顶点与水面重合，上方为空气域(αa=1)，下方为水域(αa=0)。初始速度为-6.15 m/s，楔形体入水按指定规律运动(图9)。

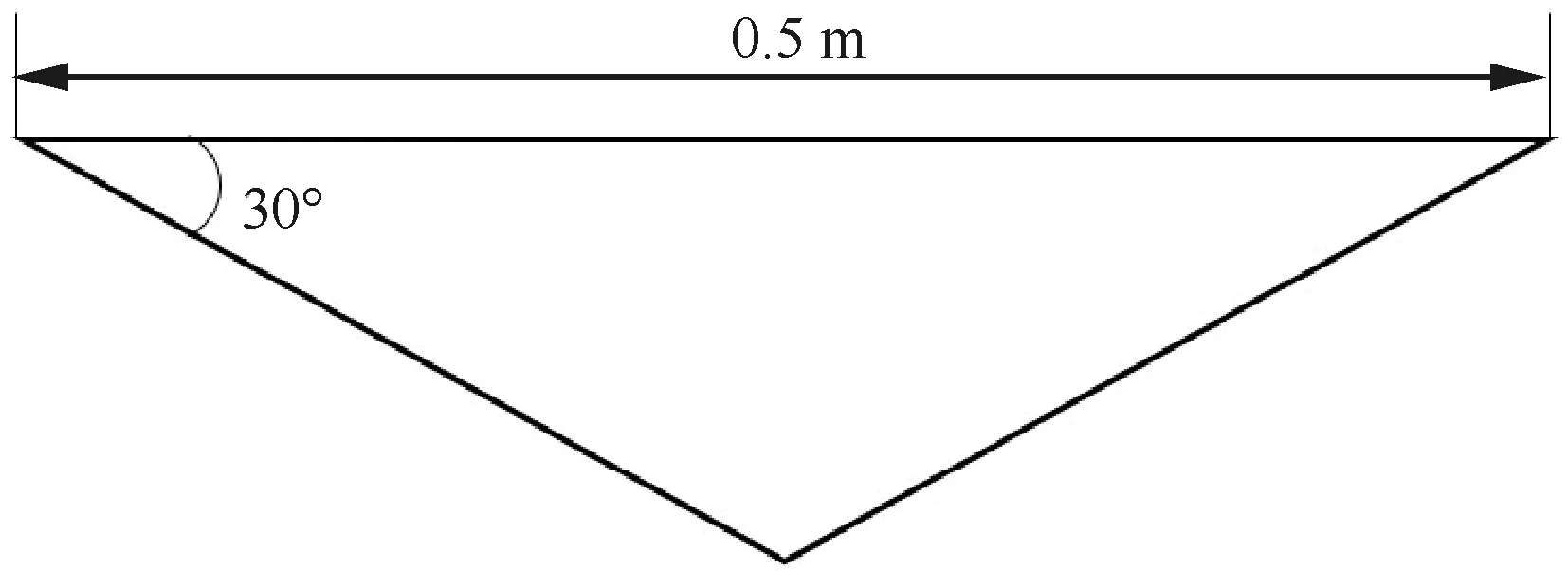
图7 楔形体横截面[26]

图8 网格计算域及初始位置

图10为楔形体入水过程中不同时刻自由液面的变形情况，计算域随楔形体移动，但水面始终保持在初始位置；由于楔形体对水的挤压作用，楔形体边缘形成射流。图11给出楔形体入水所受垂向力的数值解与试验结果[26]和理论解[27-29]的对比情况。在0.008 s时数值解开始偏离试验结果，数值解减少10%，在0.011 s时数值解开始偏离理论值，主要是考虑三维效应的影响。但总体来说，数值解与试验结果和理论解变化趋势始终相同，误差较小，在可接受范围内。

由于目前并没有对楔形体入波浪水面的有效试验数据与数值计算参考，在完成楔形体入静水面验证的基础上，运用相同的数值方法研究楔形体入波浪水面情况。

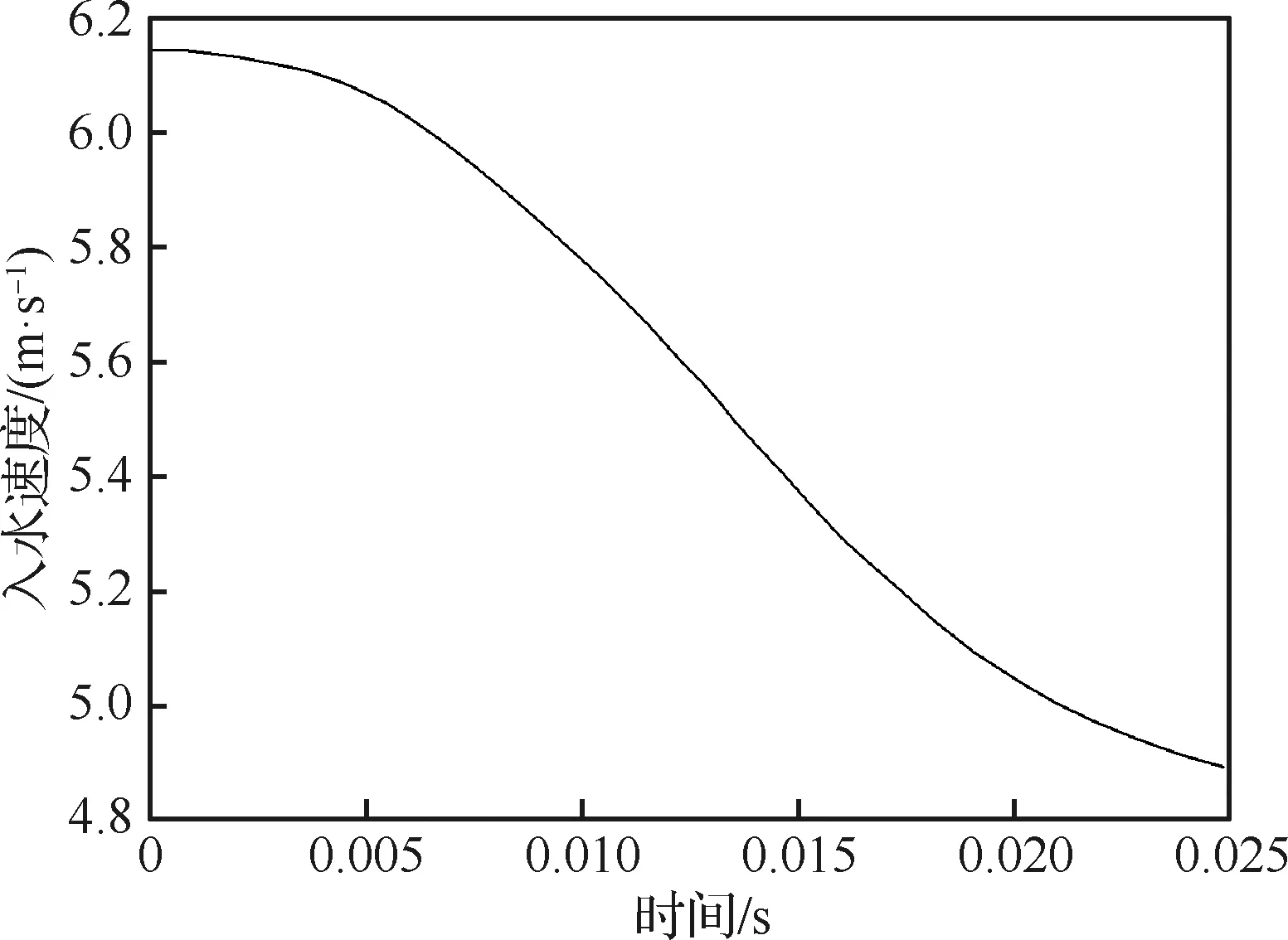
图9 楔形体入水速度变化

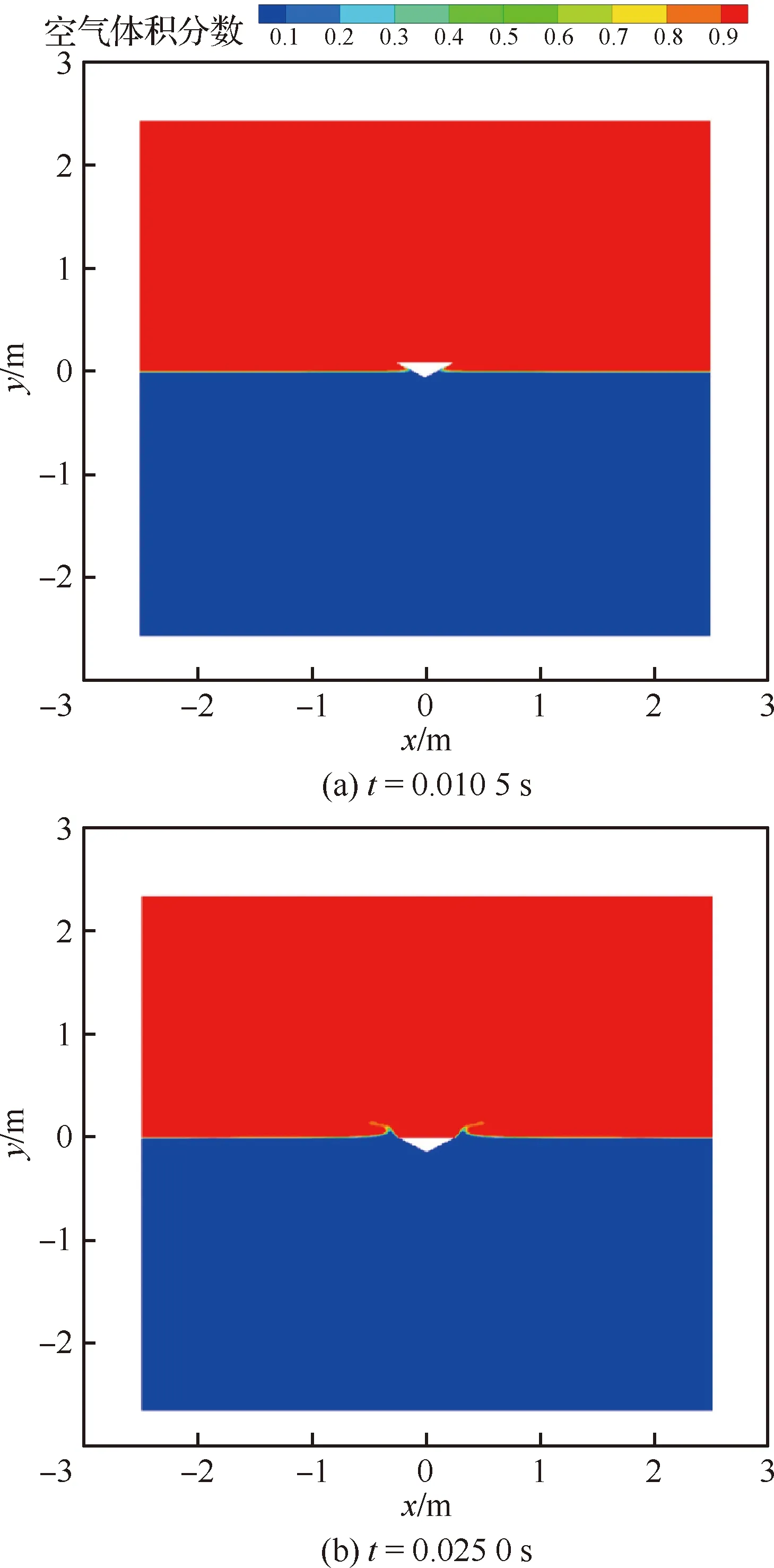
图10 楔形体入水不同时刻水面变化

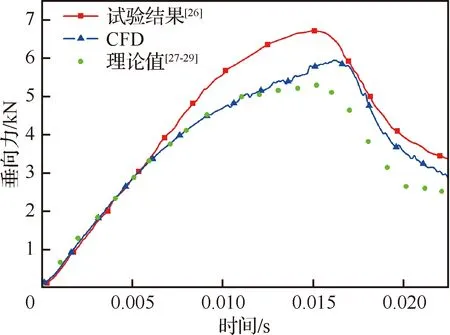
图11 楔形体垂向力随时间变化

3 计算结果与分析

3.1 二维楔形体入波浪水面数值模拟

本节研究楔形体自由(三自由度)入规则波和不规则波的波浪参数[30]为：波高H=0.12 m，波长L=2.5 m，水深d=2.4 m，周期T=1.25 s(边界条件如图3所示)。模型质量为241 kg[28]，通过数值计算得到模型绕重心质点的z向转动惯量为 9.448 kg·m2。应用整体动网格法并耦合三自由度模型对楔形体在线性规则波的波峰、波谷、平衡位置-上行速度和下行速度4个位置(图1)、平静水面和线性不规则波入水情况进行数值模拟。由于不规则波没有明显的周期性，所以当不规则波充满整个水域之后，使模型分别在t=5.0，6.0，7.1，9.0，9.5 s时间点入水，波面波形和着水位置如图12所示。保证楔形体初始速度均为-6.15 m/s的同时，分别对楔形体的垂向力、垂向速度、横向速度、横向位移和滚转角进行对比分析。

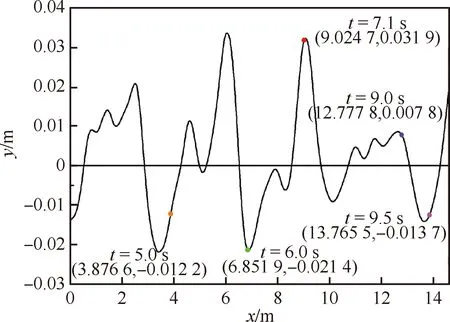
图12 楔形体入不规则波波面着水位置

楔形体在规则波不同位置入水的对比结果如图13所示。可知，模型在规则波各位置所受垂向力有先增大后减小的趋势，峰值均出现在入水初期，且平缓值相近。垂向速度变化趋势相同。模型在不同位置入横向波对横向位移的影响很小，其数值变化均少于0.01。在平衡位置-上行和下行速度位置入水过程中，模型的滚转角和横向位移变化明显，其数值变化约为波峰波谷位置处的8倍和10倍。分析原因：平衡位置处波浪内流速度变化较快，模型所受波浪力冲量较大；楔形体斜边与波浪的相对作用力也参与到楔形体的入水过程，影响了模型形态的改变。图14和图15给出了楔形体在波峰和平衡位置-上行速度处入水过程中不同时刻的水面变化，可以看出，在楔形体斜边均产生射流现象，且在平衡位置-上行速度处入水过程产生的射流显示出明显的不对称，该现象进一步验证了上述原因。

楔形体在不同时间点T入不规则波的对比结果如图16所示。可知，模型在不同时间点入水所受垂向力变化趋势相同，峰值出现于入水初期，平缓值相近。垂向速度变化趋势相同。模型在不同位置入横向波对横向位移的影响很小，其数值变化均少于0.001。T=5.0，9.5 s工况，楔形体位于类似平衡位置-上行和下行速度位置处，模型的滚转角和横向速度变化较为明显，其数值变化均为T=6.0，9.0 s工况的4倍左右，形成原因同楔形体入规则波情况相同。在T=6.0 s工况中，模型的滚转角出现由正向负、横向速度和横向位移出现由负向正的反向变化，主要考虑楔形体两侧斜边均与波浪产生相对作用力的影响。图17给出楔形体在T=7.1 s时间点入不规则波波浪水面过程中不同时刻T的水面变化，可见在楔形体斜边产生射流现象。

图13 楔形体入规则波波浪水面的载荷及运动响应结果

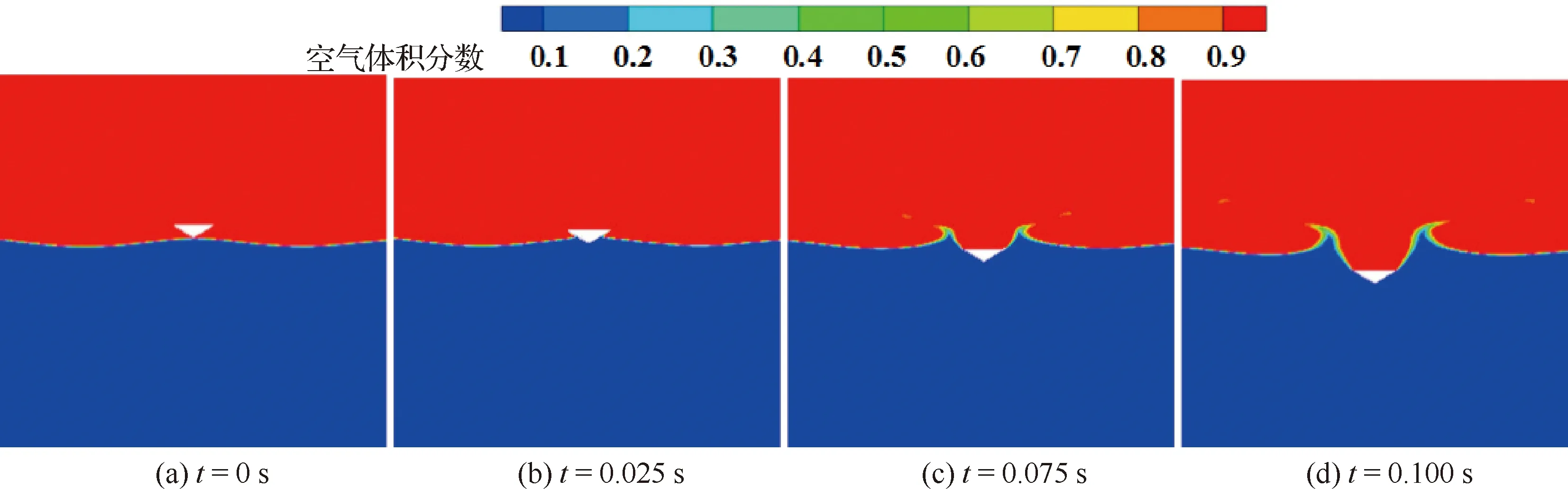
图14 楔形体在波峰处入波浪水面变化

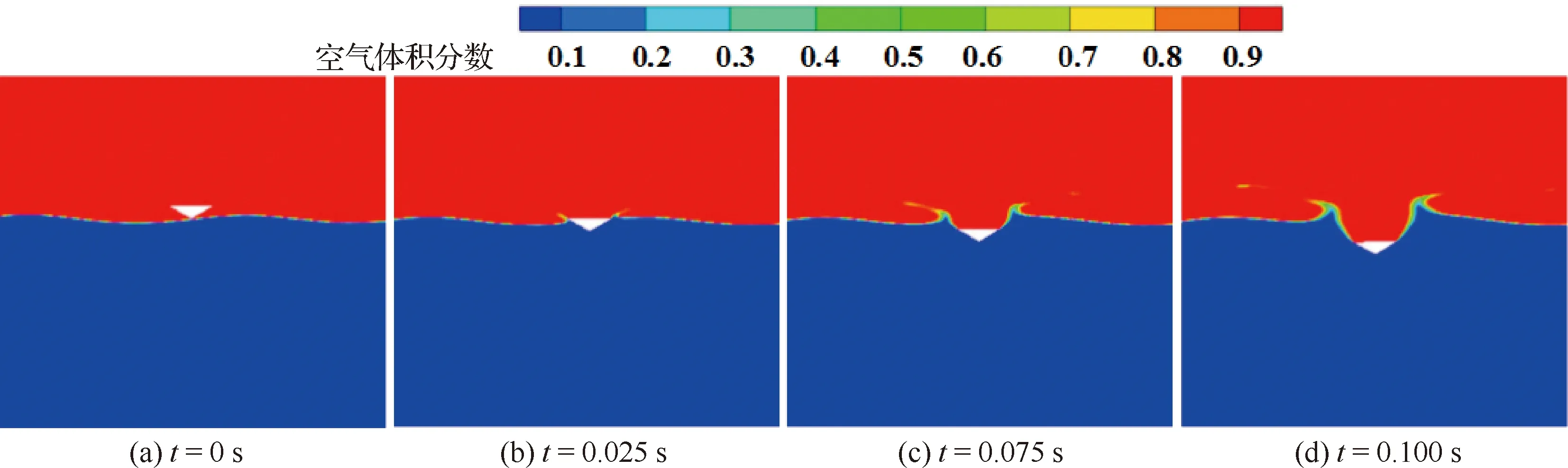
图15 楔形体在平衡位置-上行速度处入波浪水面变化

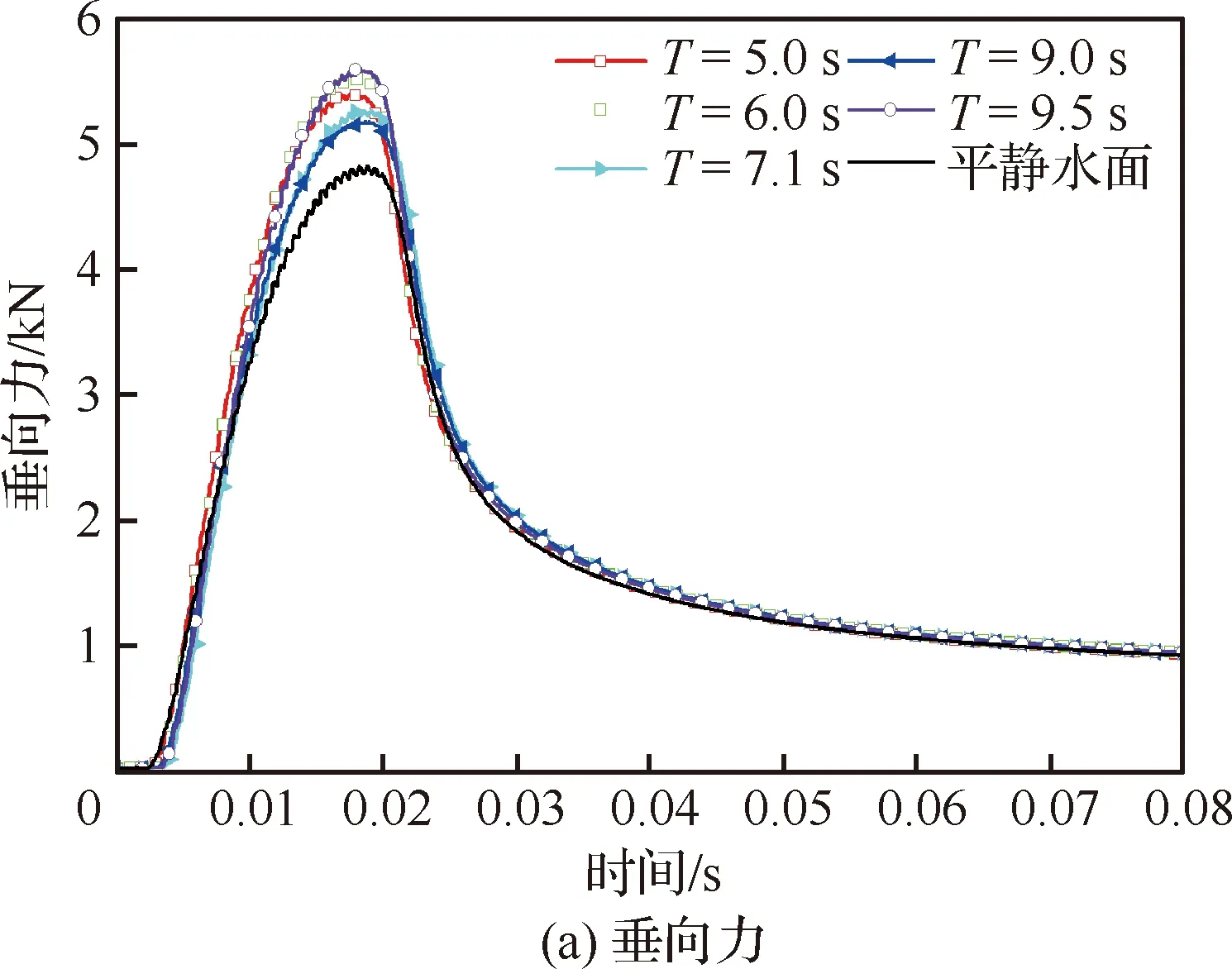
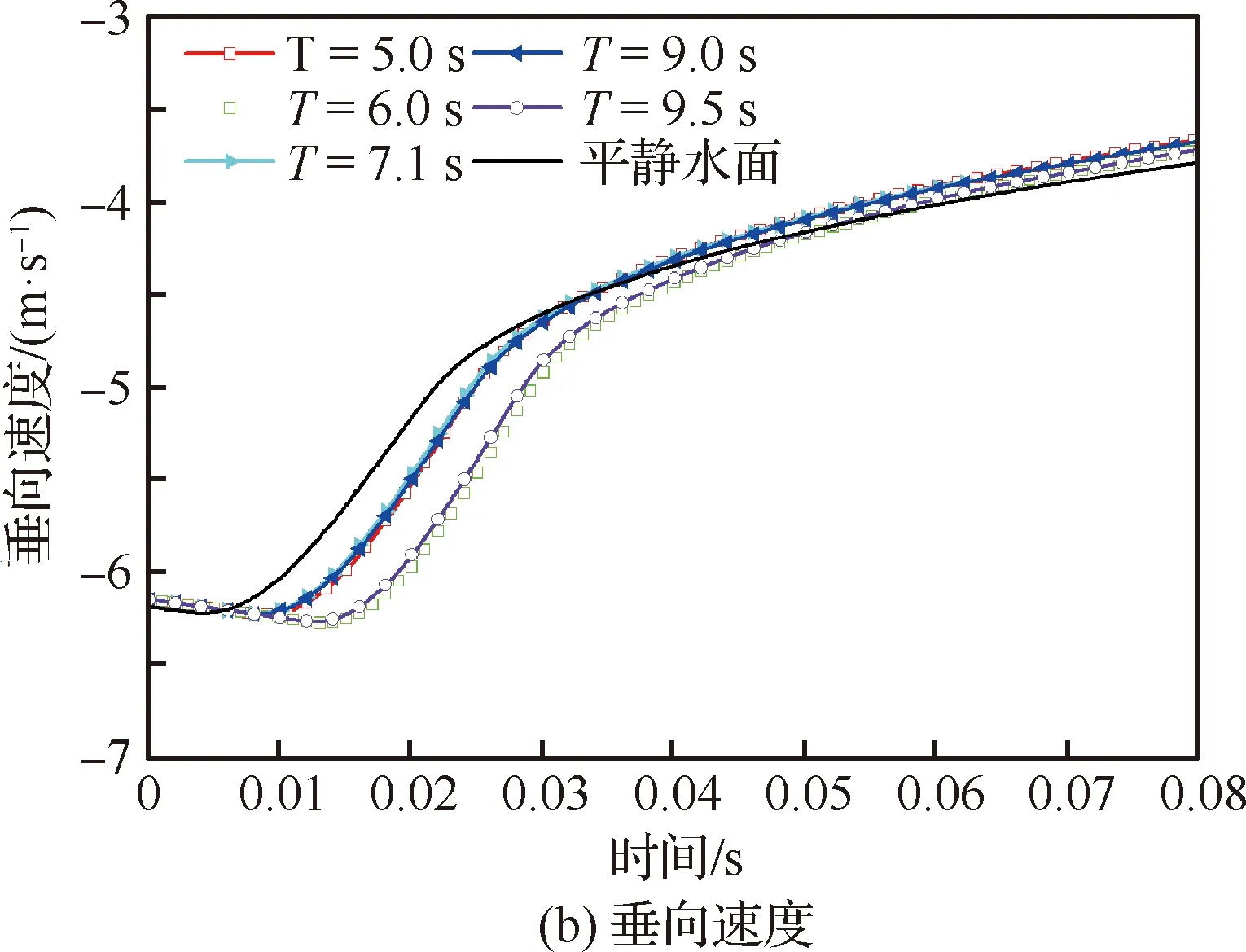
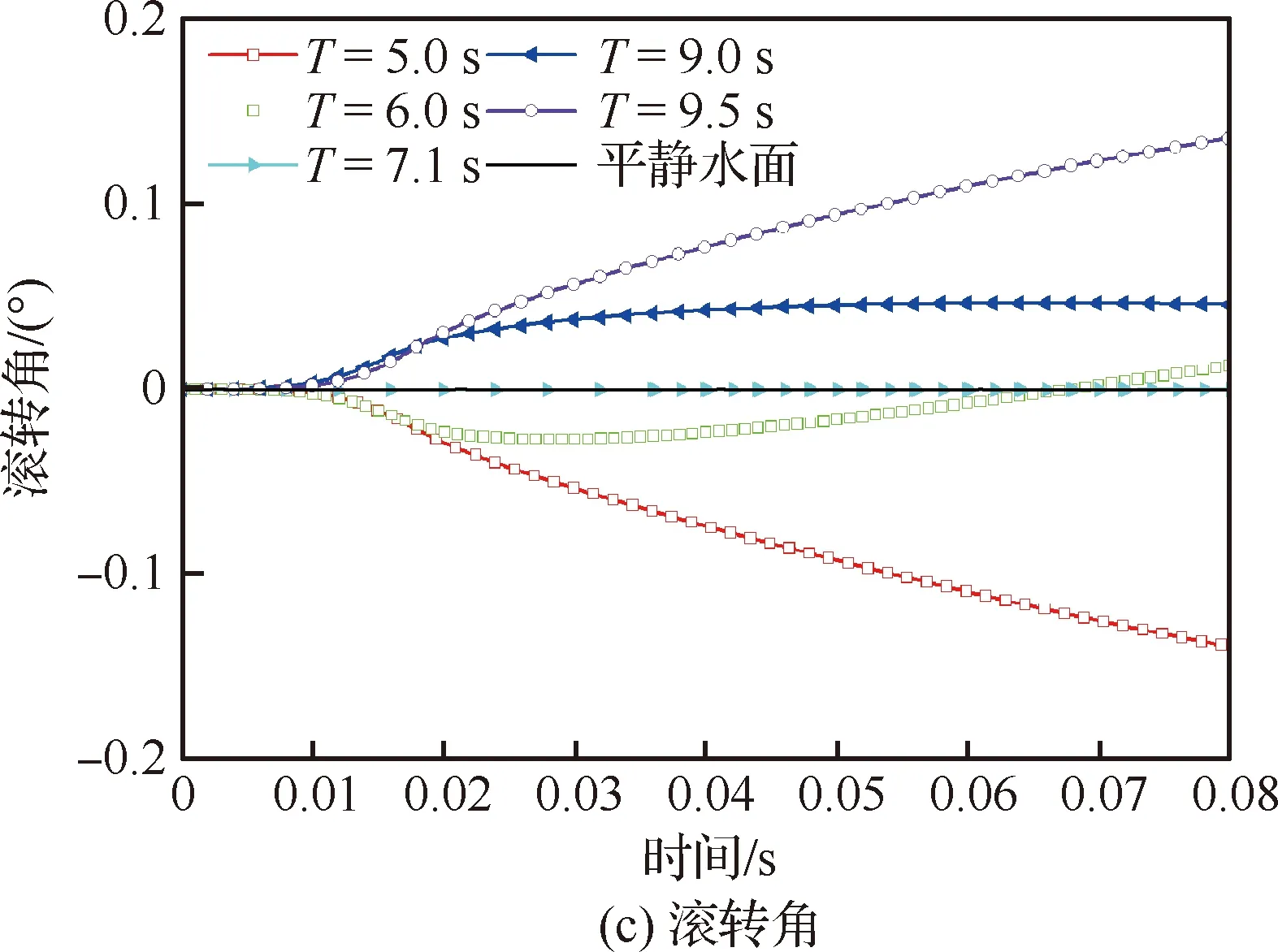
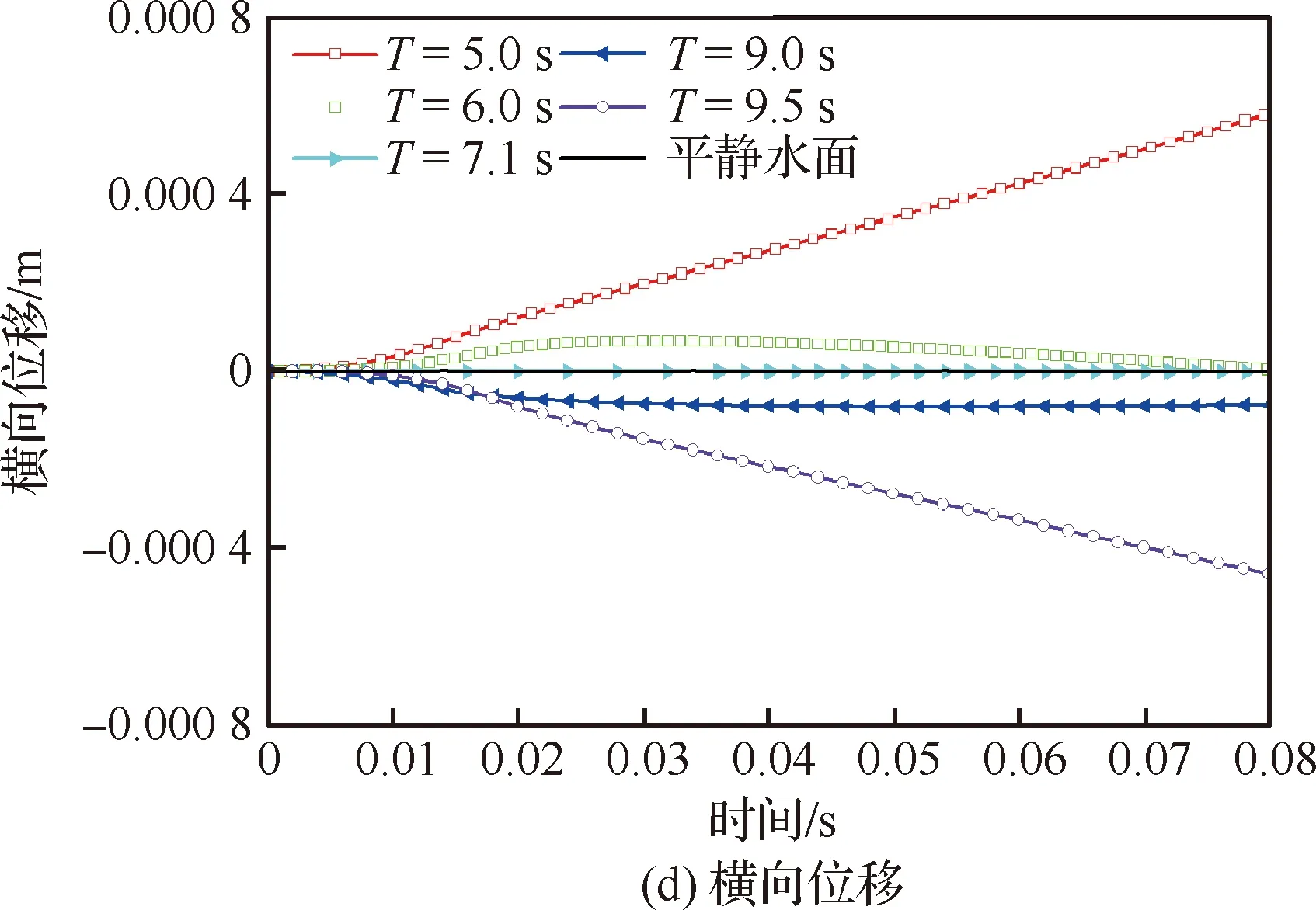
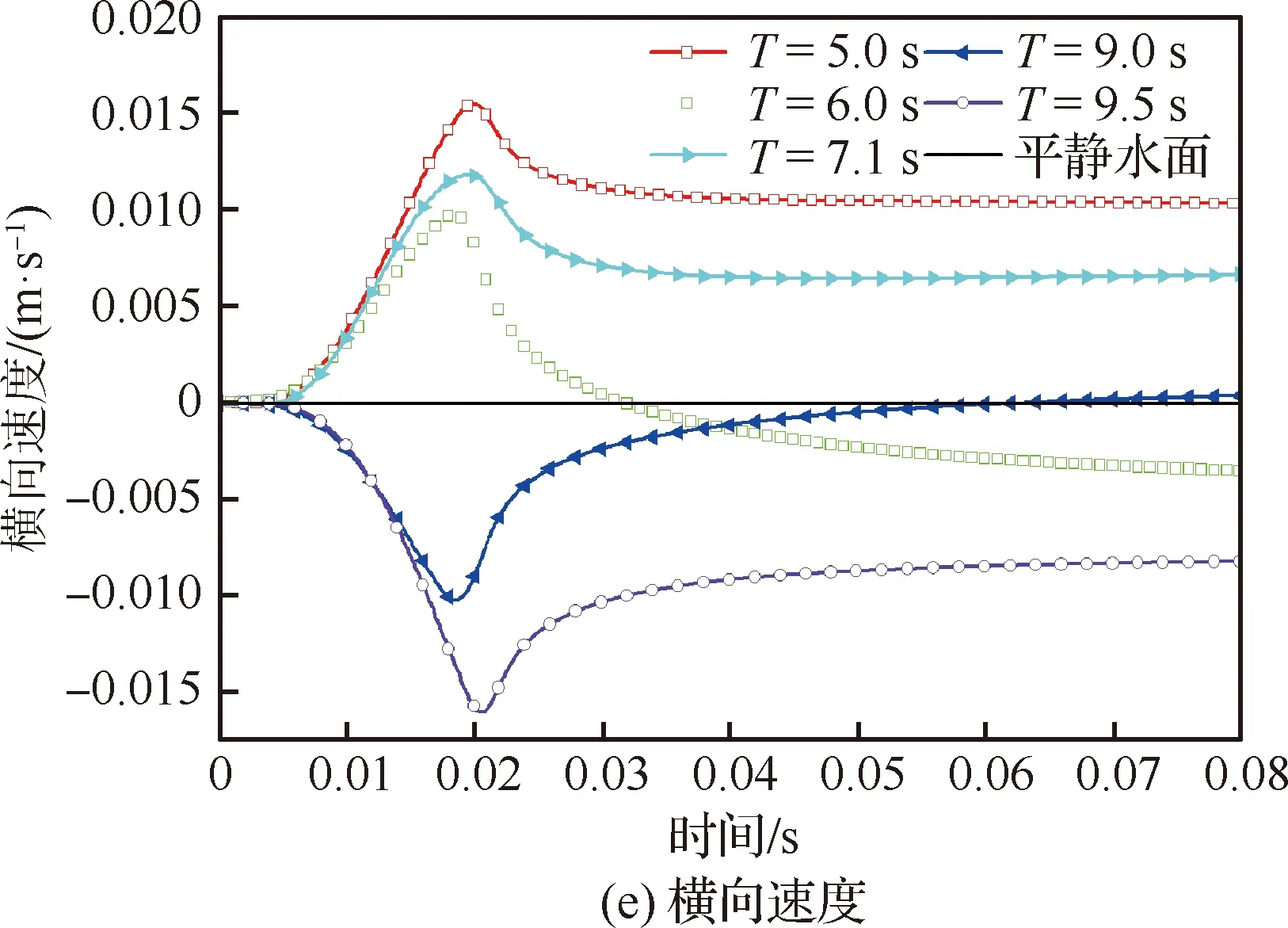
图16 楔形体入不规则波波浪水面的载荷及运动响应结果

图18给出楔形体在平衡位置-下行速度处和在T=7.1 s入不规则波后0.06 s时的计算域变化。可以看出，包含边界在内的整个计算域均随模型的运动而运动，波形保持完整的同时，液面捕捉良好且很好地耦合了三自由度模型。不规则波情况下的计算域运动策略与入规则波相同，可以说整体动网格法很好地适用于速度入口造波法和物体着水运动。

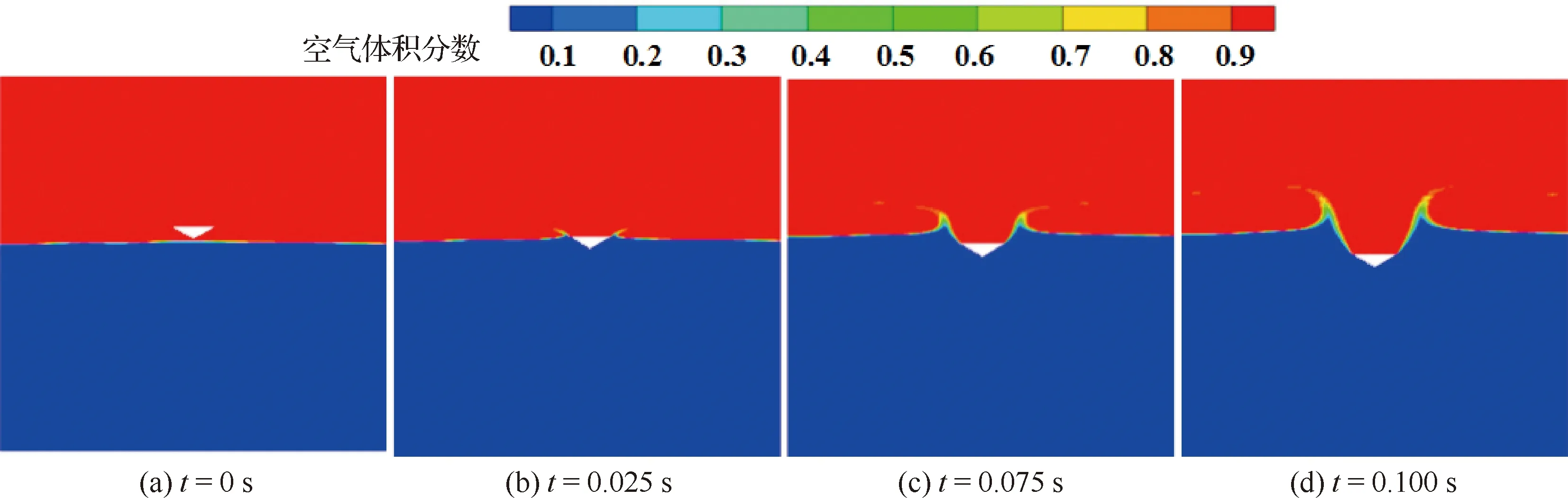
图17 楔形体在T=7.1 s入不规则波波浪水面不同时刻水面变化

3.2 三维楔形体入规则波波浪水面数值模拟

本节研究三维楔形体自由(六自由度)入规则波情况。波浪水面参数同3.1节。楔形体截面与图7相同，展长为1 m，模型如图19所示。楔形体质量采用中国特种飞行器研究所进行水箱试验的数据，即406 kg。通过数值计算得到模型绕重心质点的转动惯量分别为Iox=34.303 kg·m2，Ioy=4.699 kg·m2，Ioz=38.063 kg·m2。二维模型和三维模型绕重心质点转动惯量的不同主要考虑模型自身属性和三维效应的影响。由3.1节可知，楔形体在规则波波峰和波谷位置处入水数值变化趋势相似，在平衡位置-上行和下行速度处入水数值变化趋势相似。在不影响研究目的的同时进行简化运算，本节选取规则波波峰和平衡位置-上行速度位置，研究三维楔形体入规则波情况。

图19 三维楔形体模型

计算及对比结果如图20所示，可知，三维楔形体在规则波波峰和平衡位置-上行速度所受垂向力均出现先增大后减小的趋势，峰值出现在入水初期，且平缓值相似。垂向速度变化趋势相同。模型在不同位置入横向波过程对俯仰角、偏航角和横向位移的影响很小，其数值变化均少于0.01；而对滚转角影响较大，在平衡位置-上行速度处的滚转角数值变化约为波峰的4倍。其形成原因与二维楔形体入规则波相同。

图21给出楔形体平衡位置-上行速度处入水过程中不同时刻的水面变化。三维楔形体入水后计算域变化如图22所示。

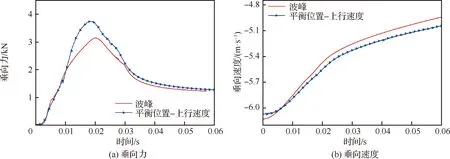
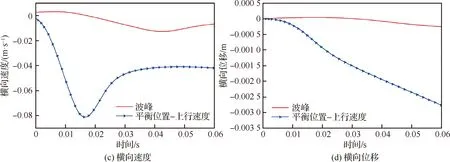
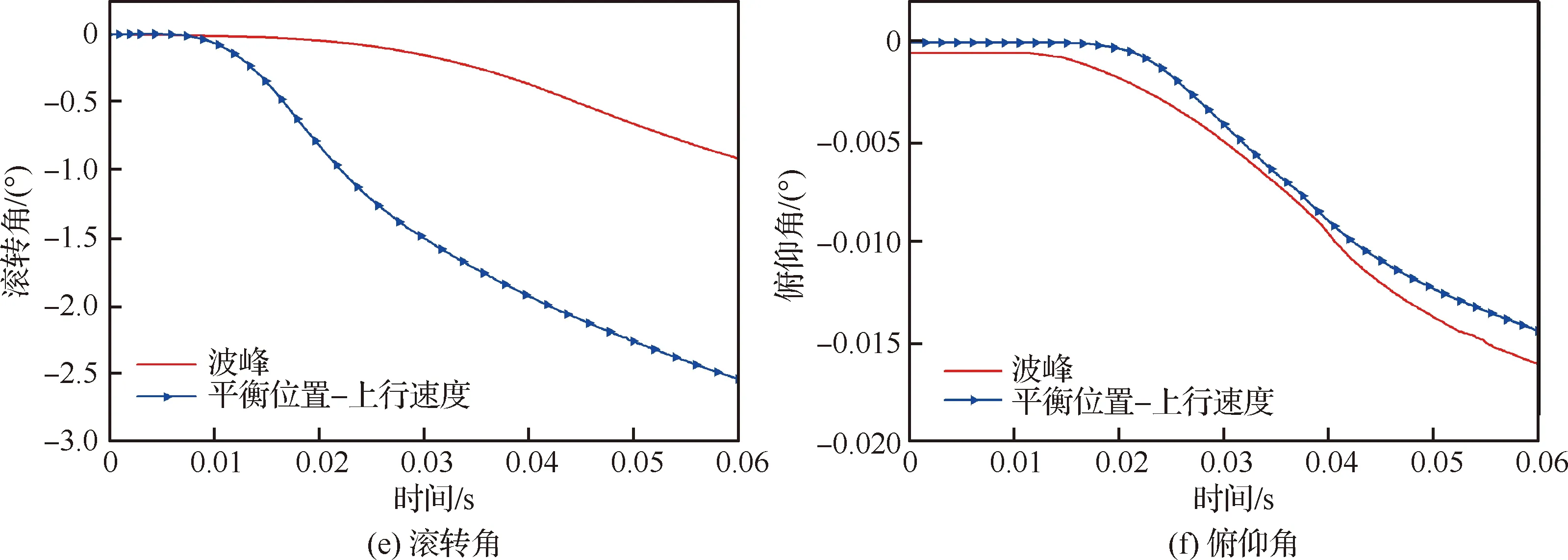
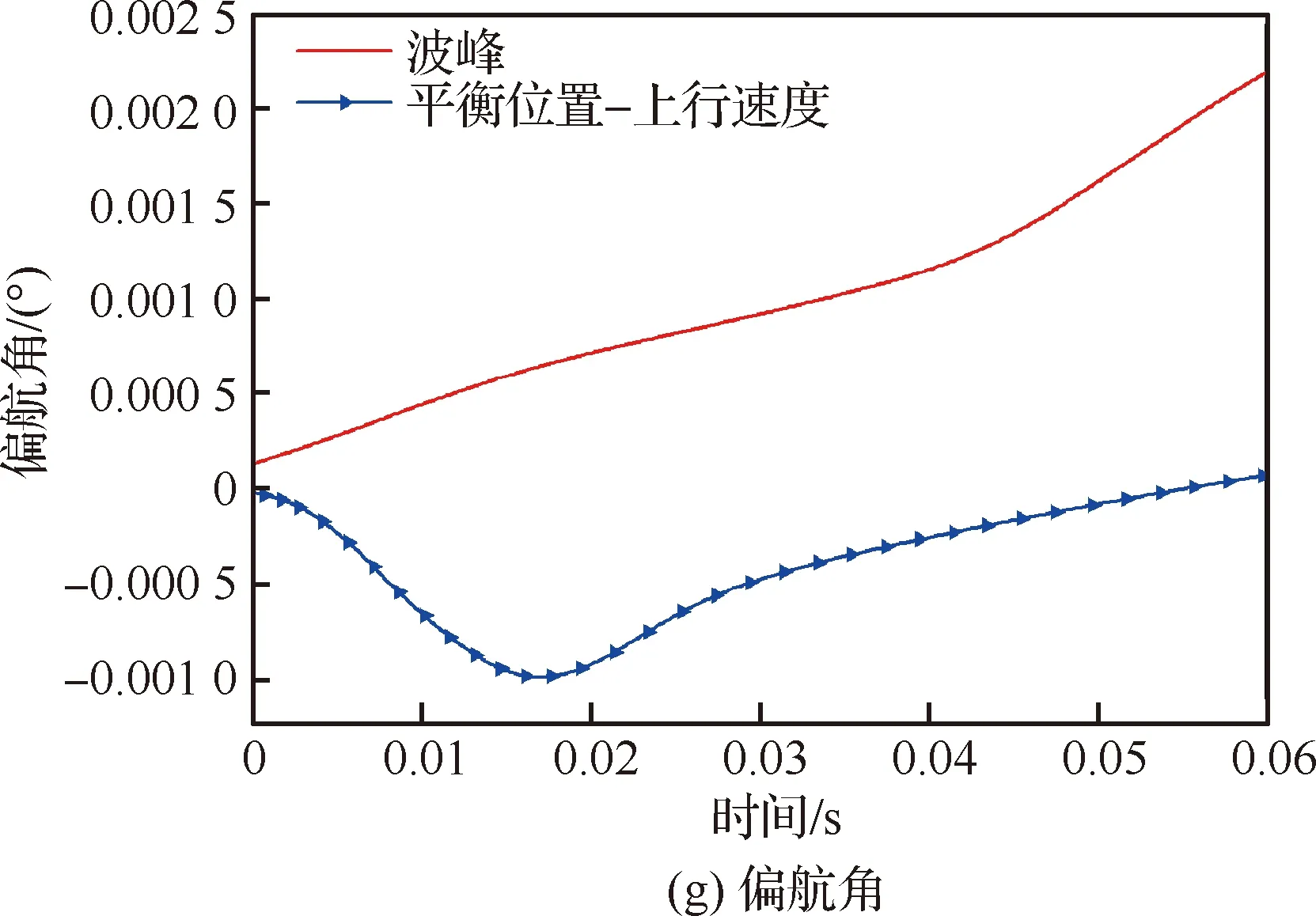
图20 三维楔形体入规则波波浪水面的载荷及运动响应结果

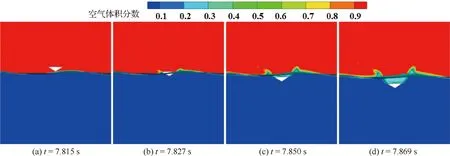
图21 三维楔形体在平衡位置-上行速度处入波浪水面不同时刻水面变化

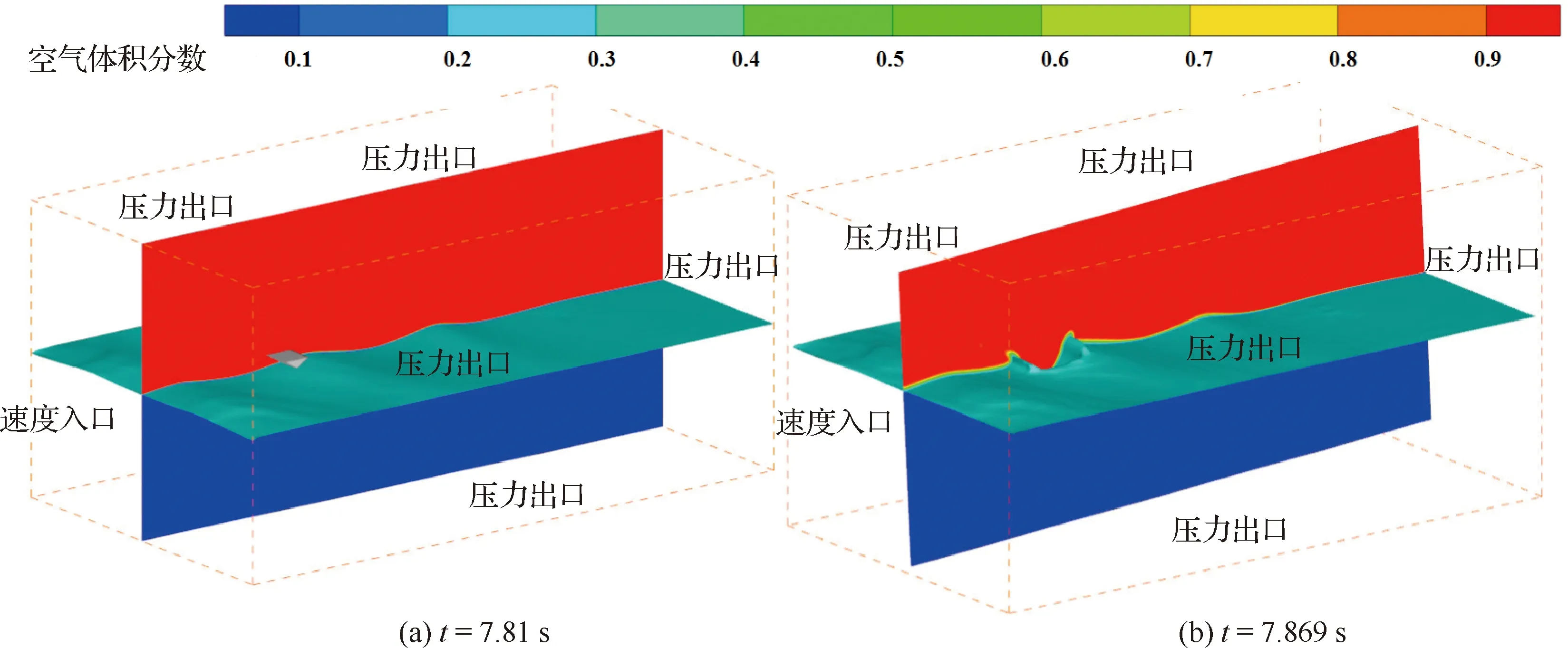
图22 三维楔形体在平衡位置-上行速度处入水计算域变化

4 结 论

1) 采用结合整体动网格法的速度入口造波法和VOF液面捕捉技术，成功构造数值波浪水池，线性规则波和线性不规则波数值解与理论解析解基本吻合，偏差为1%。

2) 数值模拟二维楔形体分别在规则波波峰、波谷、平衡位置-上行速度和下行速度4个位置处自由入水，其垂向力峰值均出现在入水初期。楔形体在平衡位置-上行和下行速度处入水对模型的滚转角、横向速度和横向位移变化影响较大，其数值变化约为波峰波谷位置处的8倍、4倍和10倍。主要考虑该处波浪内流速度较快，模型所受波浪力冲量较大，且楔形体斜边与波浪的相互作用力也参与到模型入水过程。

3) 当不规则波充满水域后，数值模拟楔形体在5个随机时间点入不规则波情况。在波浪内流速度较大处，模型的滚转角、横向位移和横向速度均出现明显变化。在t=6.0 s工况，数值出现由正到负或由负到正的反向变化，主要考虑楔形体两侧斜边均与波浪产生相互作用力。

4) 数值模拟三维楔形体在规则波波峰和平衡位置-上行速度自由(六自由度)入水。三维楔形体在入水过程中所受垂向力出现先增大后减小的趋势，垂向力峰值均出现在入水初期，且平缓值相似。垂向速度和俯仰角变化趋势相同。模型在不同位置入横向波过程对俯仰角、偏航角和横向位移的影响很小，其数值变化均少于0.01；而对滚转角影响较大，且在平衡位置-上行速度处的滚转角数值变化约为波峰的4倍。其形成原因与二维楔形体入规则波情况相同。

5) 整体动网格法结合速度入口造波法、VOF液面捕捉技术并耦合三/六自由度模型数值模拟楔形体入波浪水面情况较好，且波面保持完整。