风扇出口导向叶片低噪声设计Ⅱ：数值验证

郑文涛，蒋永松，赵航，潘若痴，赵勇

中国航发沈阳发动机研究所，沈阳 110015

对于当代民用航空飞机，尽管机体噪声在飞机着陆时也是重要的噪声分量，但航空发动机的噪声仍然是最为主要的噪声来源，特别是发动机中的风扇噪声，无论是在起飞还是降落阶段，在总噪声中都占有较大的比重[1-2]，而转/静干涉噪声又是风扇噪声的重要组成部分[3-4]。因此，对风扇噪声的控制仍是当前研究的重点，开展针对风扇的低噪声设计对于满足人们日益增长的航空坐乘舒适性需求和环境噪声限制要求具有重要意义。

风扇的低噪声设计并非是孤立的，在设计过程中必须在提高风扇声学性能的同时保证风扇的气动性能，但在工程设计过程中，声学性能和气动性能的满足往往并不同步，二者存在此消彼长的情况，因而必须建立风扇气动/声学一体化设计流程，研发气动与声学的交互设计方法，实现声学优化设计对气动设计的快速反馈。为此，在风扇低噪声设计系列文章的第1篇文章中[5]，建立了针对外涵出口导向叶片(Outlet Guide Vanes， OGV)的基于通流设计的气动/声学一体化设计方法，系统研究了OGV轴向掠形与周向倾斜对转/静干涉噪声的影响[6-8]，优选出掠形角与倾斜角的最佳组合，并以此为基础，进一步采用遗传算法对某大涵道比涡扇发动机风扇/增压级的OGV开展了参数化优化设计，最终获得了2个低噪声优化方案。

为了满足工程设计的需要，保证设计迭代的快速性，优化过程中采用了基于三维升力面理论[9-11]的解析预测模型，在建立转/静干涉噪声预测模型的过程中，对实际问题进行简化[12]，例如，将真实的发动机管道简化为等直径环管，叶片简化为无弯度、无厚度的平板；使用了NASA早期发展的尾迹模型[13]，该模型是基于对一系列转子尾迹的试验数据进行统计整理得出的，得出这些试验数据的年代较早，这些风扇转子的特征与现代大涵道比发动机的风扇转子有较大的差别，这无疑也增大了解析模型的预测误差。因此，在建立的气动/声学一体化设计流程中还强调了对方案进行声学性能的详细评估。

为了进行声学性能详细评估，需要采用高精度数值仿真方法(如完全非定常数值仿真)，以获得流场和声场的全部信息，但针对风扇和压气机的完全非定常方法计算量巨大、周期长，很难适用于设计阶段。因此需要一种既能捕捉转/静干涉信息，又能降低计算成本的数值方法。非线性谐波法(Nonlinear Harmonic Method,NLH)[14-15]使用单通道网格在频域求解控制方程，可以采用定常计算的各类加速算法，既能捕捉在叶片通过频率(Blade Passing Frequency,BPF)及其谐频处相邻叶排相互影响，又能节省计算时间，满足方案设计过程中的噪声分析要求。因此本研究采用NLH方法对原方案和优化方案进行流场数值模拟，获取与转/静干涉噪声源相关的流场信息。获得声源流场信息后，进一步采用Wilson等[16-17]发展的波分解理论，详细分析原方案和优化方案的声源模态信息，量化OGV的低噪声设计效果。

1 低噪声优化方案

在文献[5]中，建立了基于通流设计的气动/声学一体化设计方法，采用该方法并结合遗传算法对OGV开展了参数化优化设计，最终获得了2个低噪声优化方案A(OptimizedA，OPT-A)和优化方案B(OptimizedB，OPT-B)，相对于原型方案(Original，ORI)，OPT-A前传噪声和后传噪声分别降低9.4 dB和8.8 dB，OPT-B前传和后传噪声分别降低8.7 dB和9.6 dB[5]。

原型ORI和2个低噪声优化方案OGV的子午投影如图1所示，X和R分别为轴向和径向无量纲坐标。各方案三维结构示意图如图2所示，图中黑色为风扇转子及ORI方案的OGV，深灰色为OPT-A方案的OGV，浅灰色为OPT-B方案的OGV。

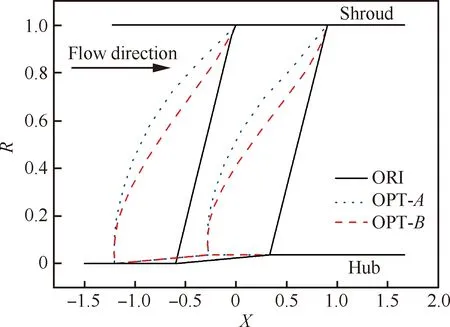
图1 OGV优化方案的子午投影

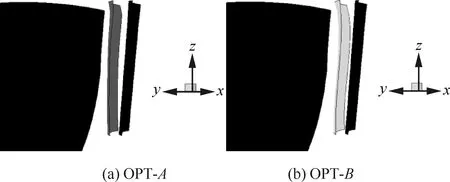
图2 OGV优化方案叶片三维构型

2 气动特性

根据气动/声学一体化设计流程，在完成对方案的声学快速评估和优化设计后，需对方案的气动性能进行评估，以保证低噪声设计不影响原风扇/增压级的气动性能。为此，采用FINETM/Turbo[18]定常雷诺平均Navier-Stokes(Reynolds Average Navier-Stokes， RANS)算法对低噪声优化方案进行气动性能计算，计算分别针对起飞、设计及爬升3个状态进行，不同状态所对应的相对换算转速如表1所示。

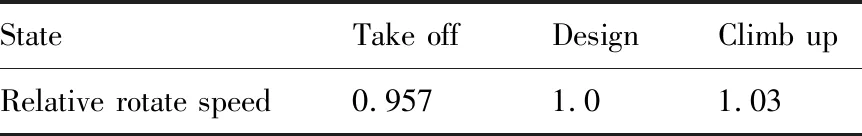
表1 风扇各状态相对转速

表2 定常RANS计算设置

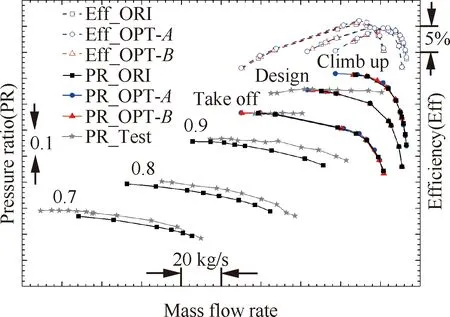
图3 OGV低噪声优化设计方案外涵气动特性

为保证数值计算的可对比性，对不同方案的不同状态均采用相同的网格绘制策略及计算设置，以期在相同的条件下对比分析不同方案的性能变化趋势。通过对比发现，在起飞转速OPT-A和OPT-B的效率特性略高于原方案；在设计转速OPT-A和OPT-B的效率特性与原方案的特性几乎重合，且OPT-A和OPT-B具有更好的裕度；在爬升转速，OPT-A的不稳定边界最靠近左侧，OPT-B与原方案的不稳定边界基本重合，3个方案的效率基本保持一致。综上所述，经低噪声优化设计后，OPT-A和OPT-B的气动性能相较原方案未出现下降。

3 非线性谐波法分析

如前言所述，由于在一体化设计过程中使用的噪声解析预测方法对实际问题进行了大量简化和近似，为了对低噪声方案的降噪效果进一步确认，需开展更高精度的声学评估。结合工程实际需求，本文使用NLH方法对低噪声设计方案OPT-A和OPT-B的转/静干涉噪声水平进行评估，并与原方案进行对比分析。

(1)

式中：扰动分量U′(t)可根据精度需求，在时间方向上进行N阶傅立叶分解,

(2)

(3)

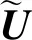
(4)

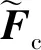
将时间平均式(3)与扰动式(4)耦合求解，即可得到非定常流场，关于NLH方法的详细论述参见文献[15]。在采用NLH方法计算过程中，为了进一步节约计算资源，省去了内涵增压级除进口导向叶片(Inlet Guide Vanes，IGV)外的所有叶排，如图4所示。

由于声源信息对数值反射十分敏感，为了降低计算域边界的反射对声源信息的影响，转/静交界面采用无反射模型，同时将风扇进口段延长至2倍风扇转子弦长，将OGV出口段延长至6倍OGV弦长，且进、出口在靠近计算域边界的网格逐渐稀疏以耗散数值反射。NLH方法的计算设置见表3。

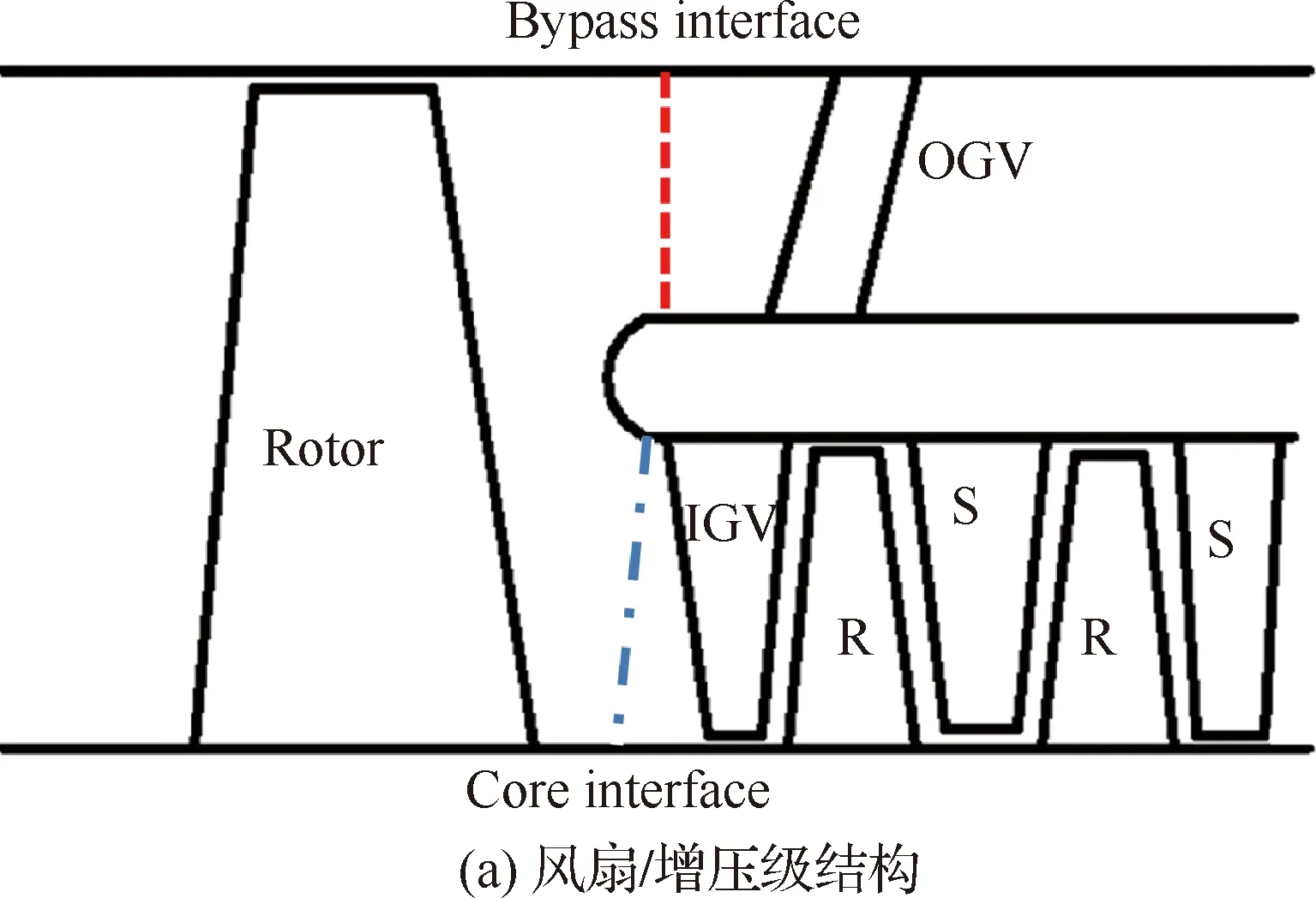
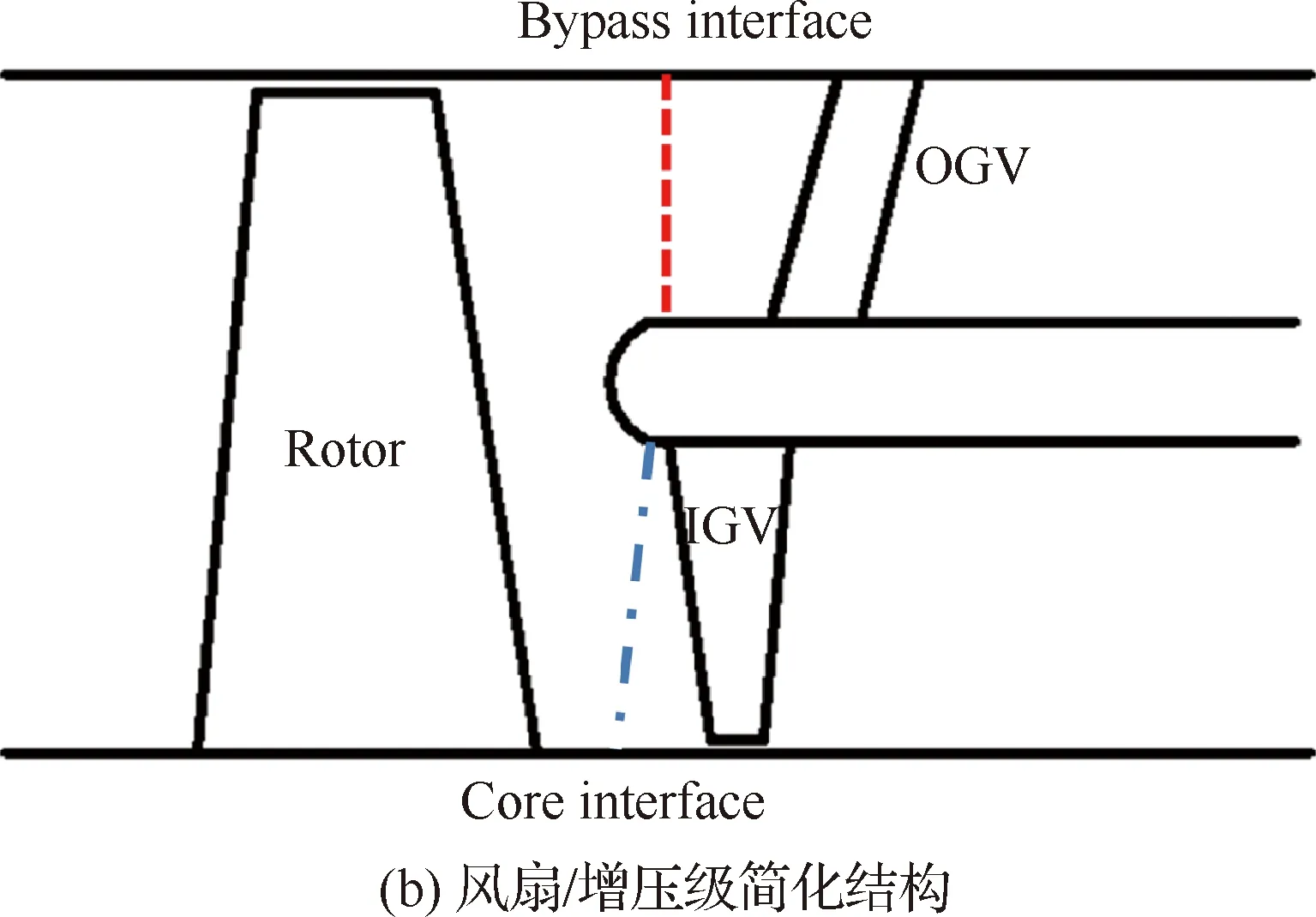
图4 非线性谐波法数值模拟结构示意图

表3 NLH计算设置

转/静干涉噪声的强弱在一定程度上决定于转子尾迹的强度，而转子尾迹的强弱又与转子的负荷状态直接相关。因此，为了尽量保证省去内涵叶排后的转/静干涉强度与实际状态保持一致，需保证转子叶片的工作状态一致，为此按如下方式进行处理。首先，使用图4(a)所示的风扇/增压级完整结构进行特性计算，针对每一转速特性线(如图3所示)，找到各转速(起飞、设计和爬升)工作点处风扇转子所对应的内涵和外涵压比，然后在进行NLH计算分析时，通过调整内、外涵出口静压，使风扇转子对应的内和外涵压比与前者一致，即对于每个工作点，分别保证虚线和点划线处压比一致，如图4所示，图中R表示增压级转子，S表示增压级静子。

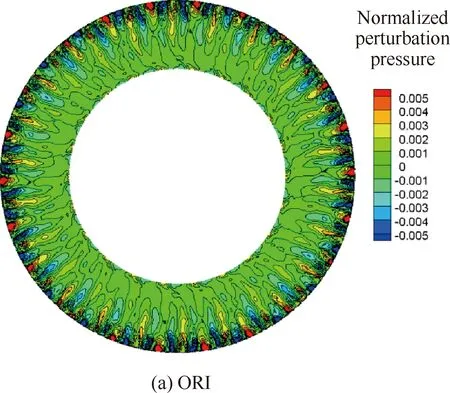
以设计状态为例，分别给出了不同方案风扇转子与OGV之间不同轴向位置的轴向速度分布，如图5所示。图中可以看出，3个方案相同轴向位置的速度分布基本一致，这在一定程度上说明了静子叶片结构改变对转子尾迹强度几乎没有影响，低噪声OGV方案的降噪效果只来源于OGV三维构型的变化导致的OGV对转子尾迹非定常响应的变化。图6与图7分别给出了3个方案OGV前、后截面无量纲脉动压力分布。对于OGV前截面的脉动压力，方案OPT-A和OPT-B受根部前移的影响，脉动压力在根部出现较强的干涉。方案OPT-A和OPT-B的OGV后截面脉动压力大幅减小，在与ORI相同的显示尺度下，OGV后脉动压力的模态特征已不可辨识。

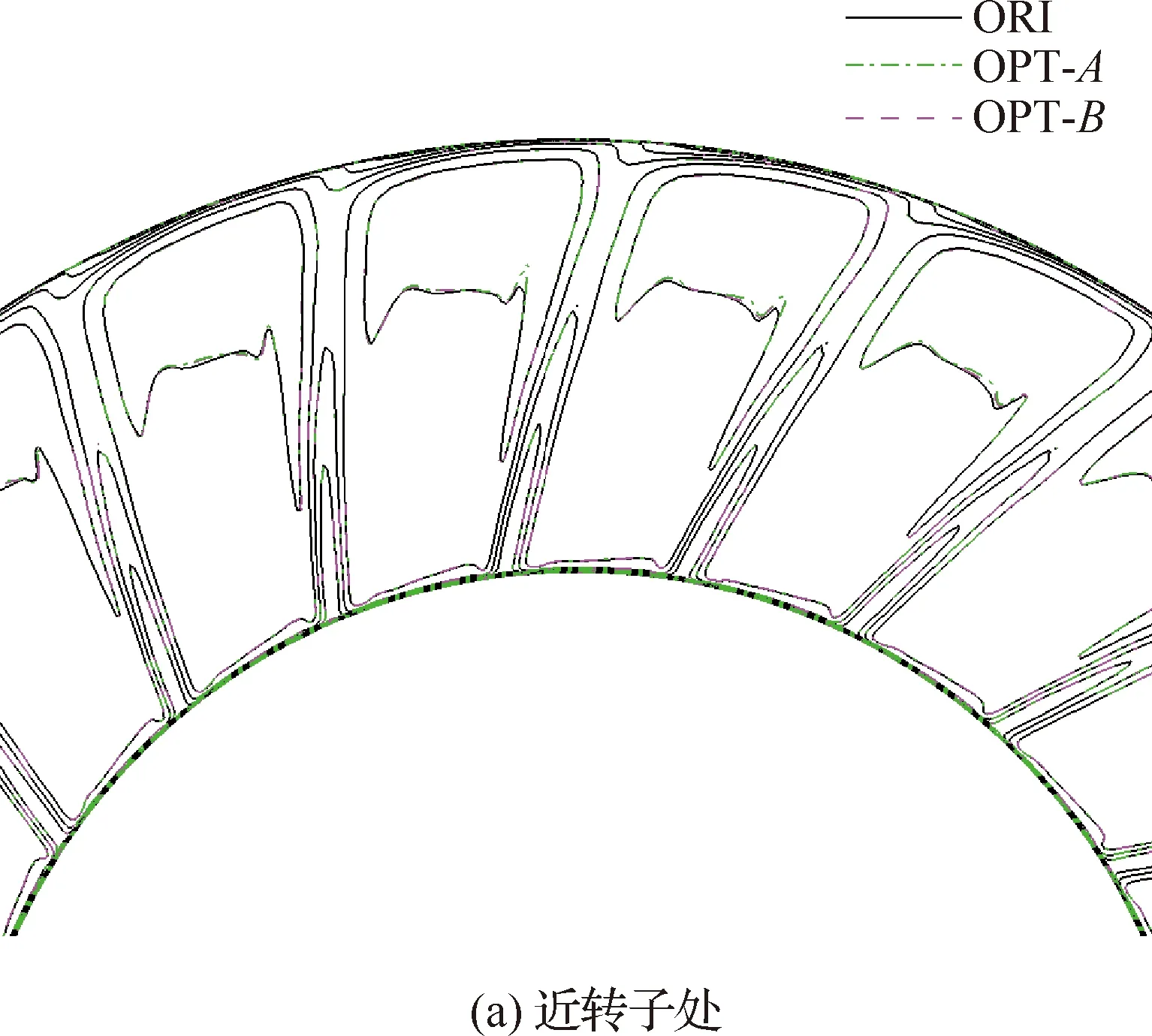
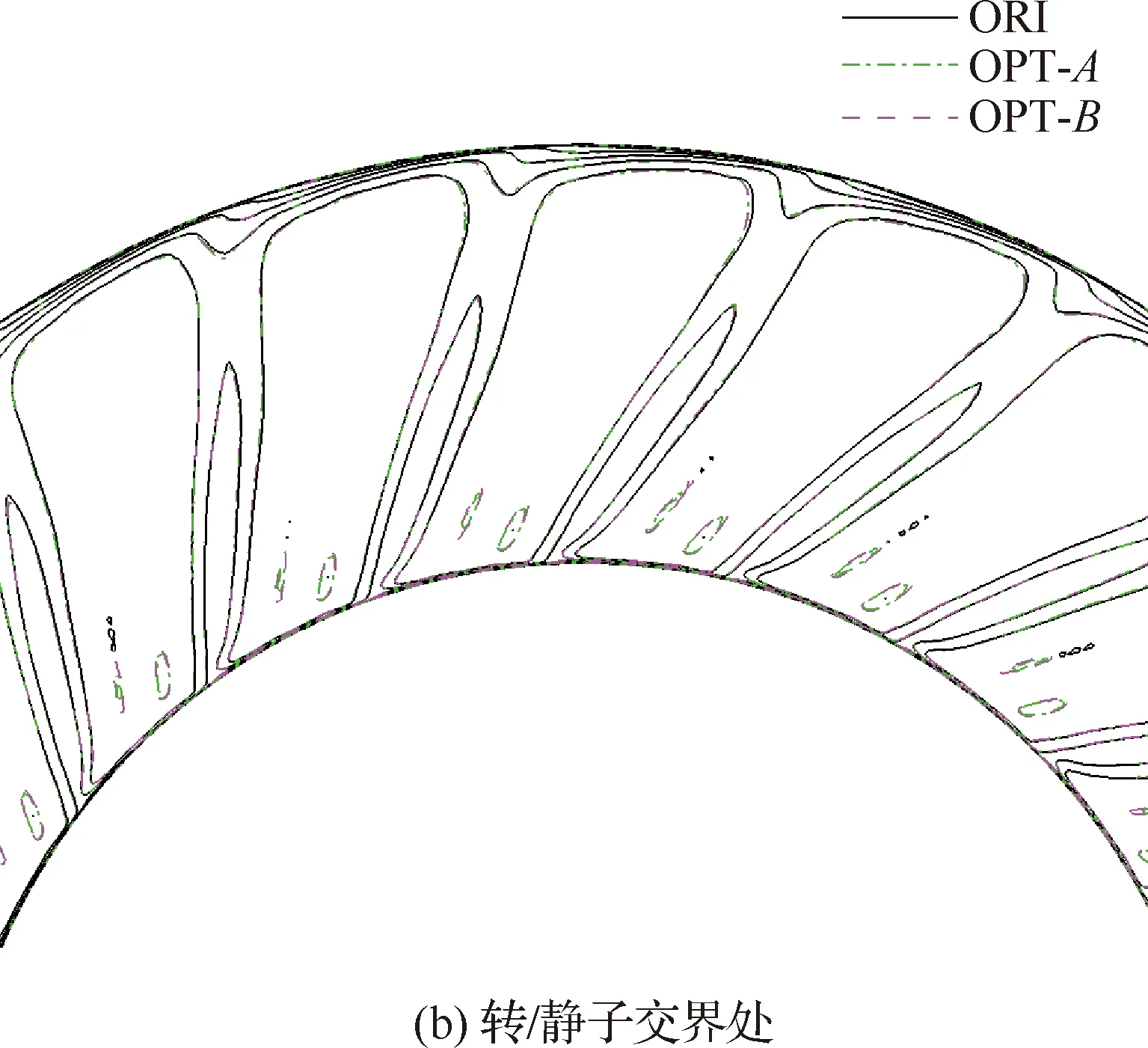
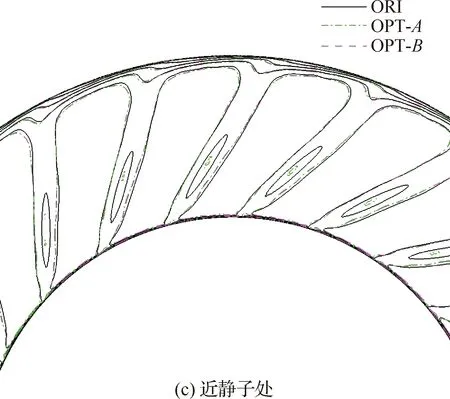
图5 转子后不同轴向位置轴向速度分布(设计状态)

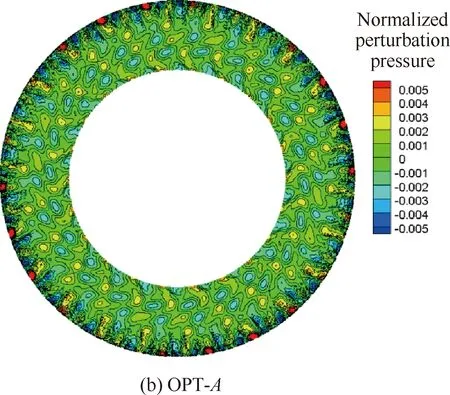
转/静干涉噪声的产生主要包括2个相互关联的过程：一是静子叶片对来流转子尾迹扰动的非定常响应；二是静子叶片响应与所在管道之间的相互作用。图8～图10分别给出了某时刻叶根、叶中和叶尖3个截面OGV叶栅槽道内无量纲脉动压力的分布。从图中可以看出，OPT-A和OPT-B方案槽道内叶根、叶中与叶尖的脉动压力较原方案均明显降低，这说明OGV对转子尾迹的非定常响应减弱，在一定程度上确认了低噪声优化设计效果。

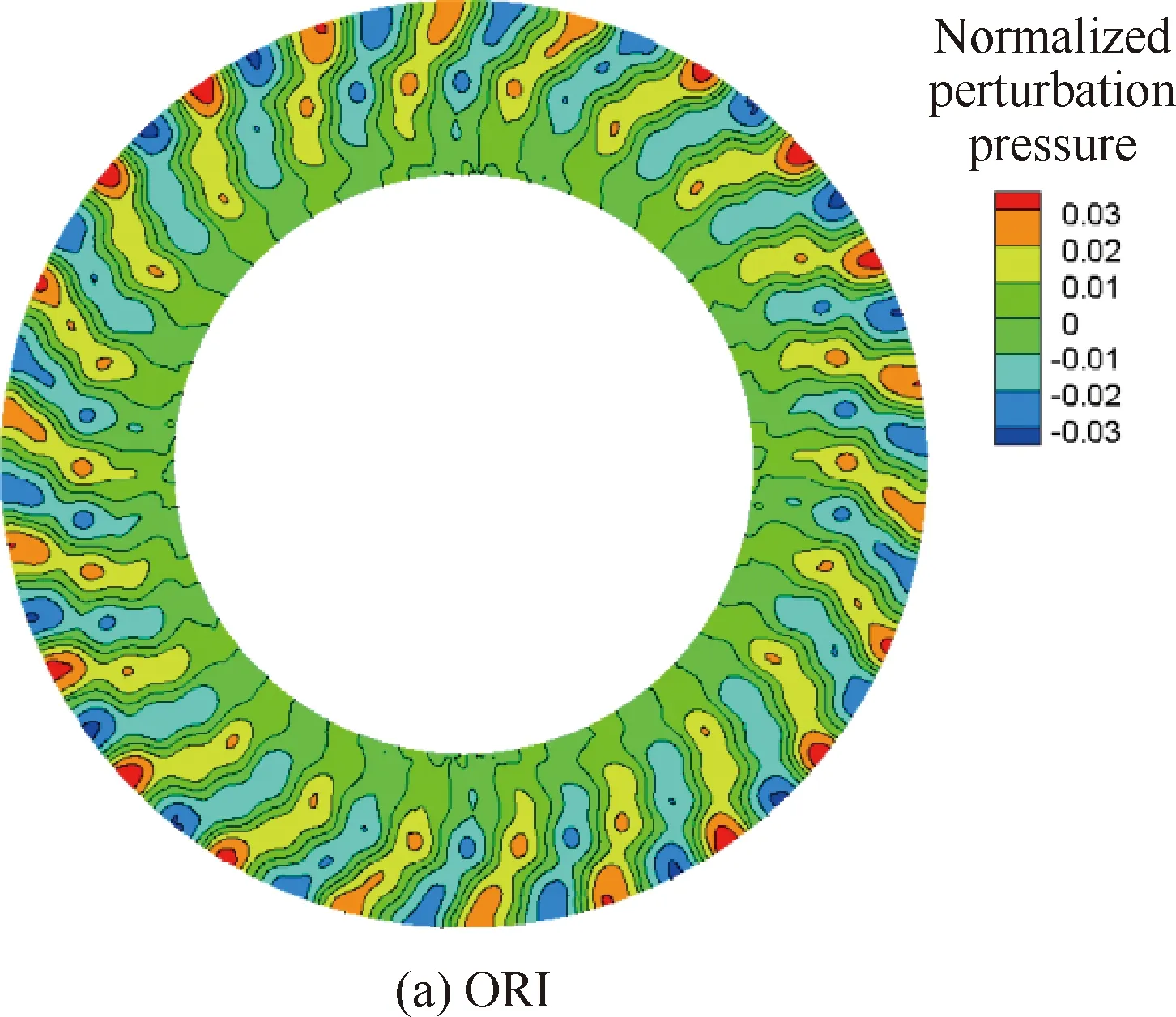
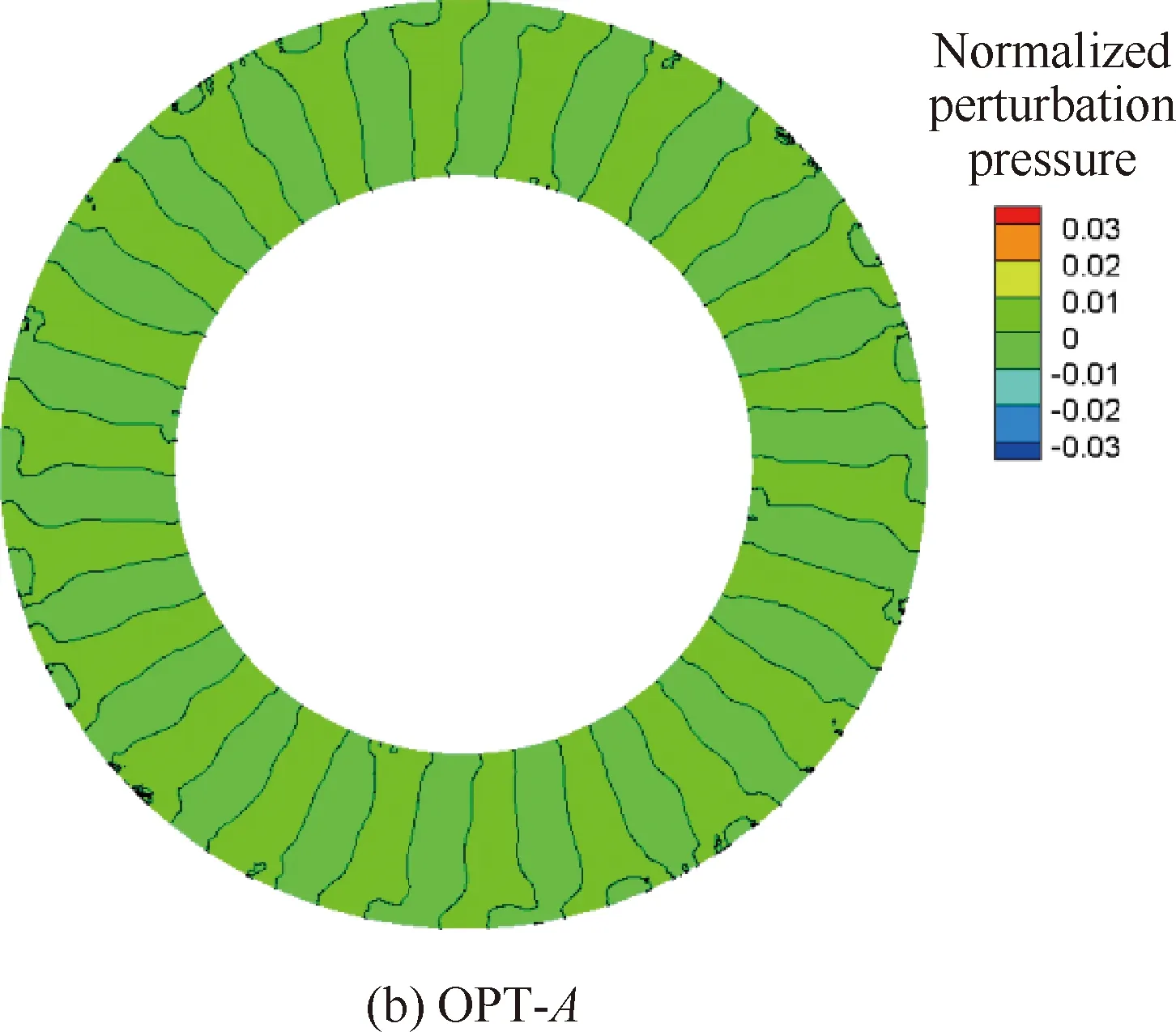
图7 OGV后截面无量纲脉动压力分布(设计状态)

图11与图12进一步分别给出了设计状态OGV吸力面和压力面上一阶无量纲化脉动压力实部和相位的分布。可以看出，吸力面的非定常响应要明显大于压力面，叶片前缘处的脉动压力最大。不同的是，低噪声设计OPT-A与OPT-B方案OGV表面脉动压力向下游快速衰减，而ORI方案仍保持较大的量值，并且沿叶高方向非定常脉动的波瓣占据了较大的叶高位置，这证明了经过轴向掠形和周向倾斜的低噪声优化设计后，有效降低了转/静干涉引起的脉动压力，相应地减小了噪声源。同时还可以看出，优化设计后叶片前缘的波瓣数明显大于ORI，这进一步证明了转子尾迹与OGV间的运动学关系是影响转/静干涉噪声的主要因素之一[19]，通过恰当选择OGV的掠形和倾斜形式，增加上游转子尾迹扫掠每个OGV叶片的数目，从而减小转/静干涉噪声。另外，从吸力面和压力面上脉动压力相位的分布可以看出，原方案的相位倾向于沿轴向变化，而经低噪声设计后，2个方案的相位均倾向于沿径向变化。实际上，从对转/静干涉噪声的控制角度来说，一方面，低噪声优化设计减小了OGV表面的非定常响应，另一方面，掠形和倾斜的合理组合，改变了OGV表面的相位分布，沿径向的相位变化增加了各声源点(将OGV声源面视为一系列点源的集合)之间的相互抵消干涉的机会，也有利于噪声的降低。起飞与爬升状态的结果与设计状态类似，不再叙述。

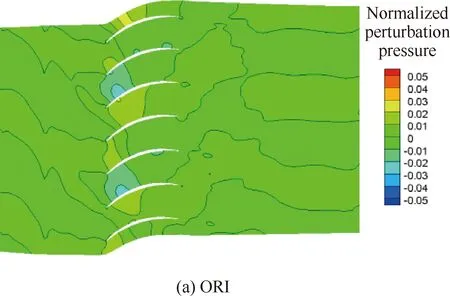
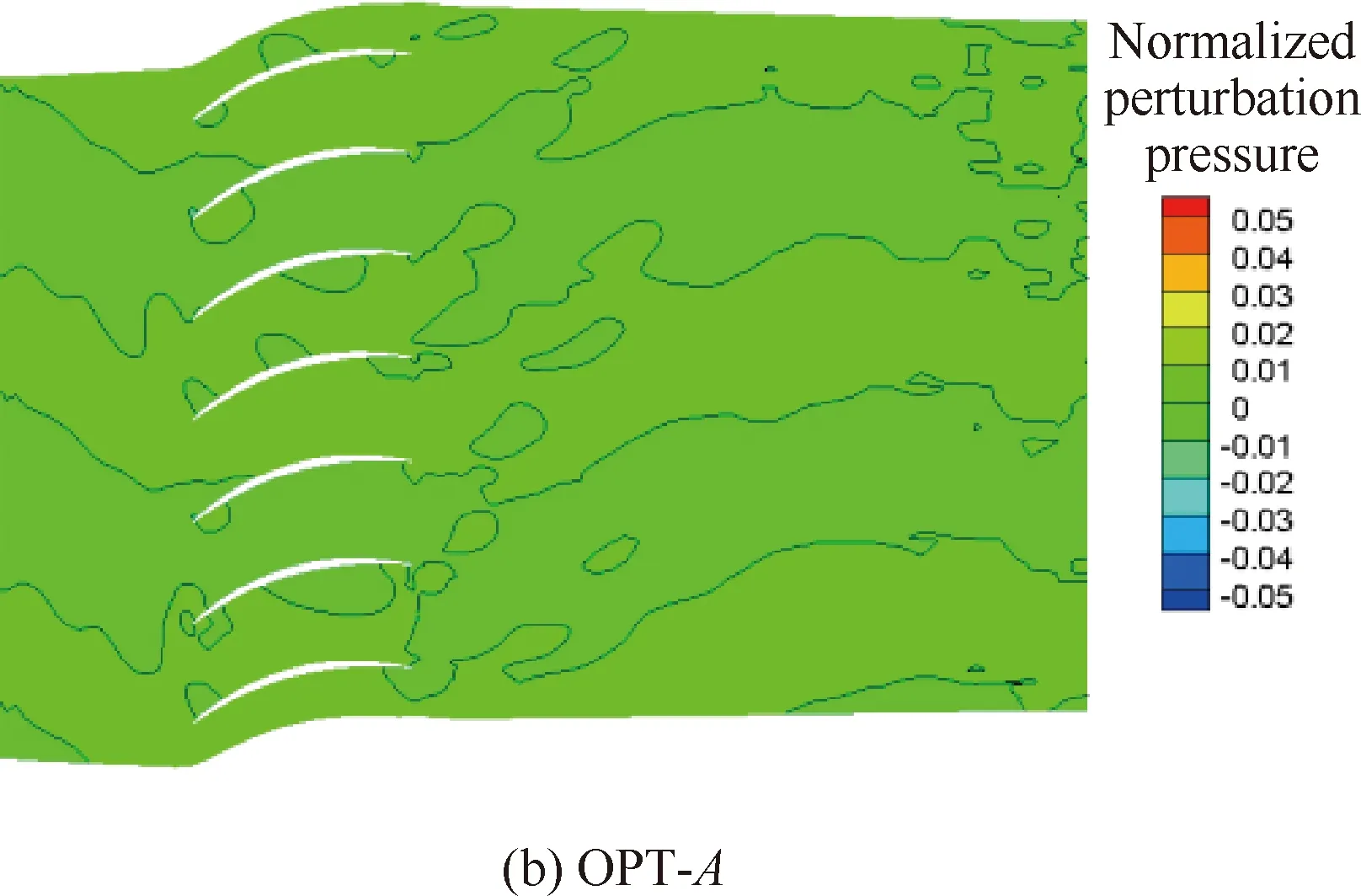
图8 OGV叶根截面处无量纲脉动压力分布(设计状态)

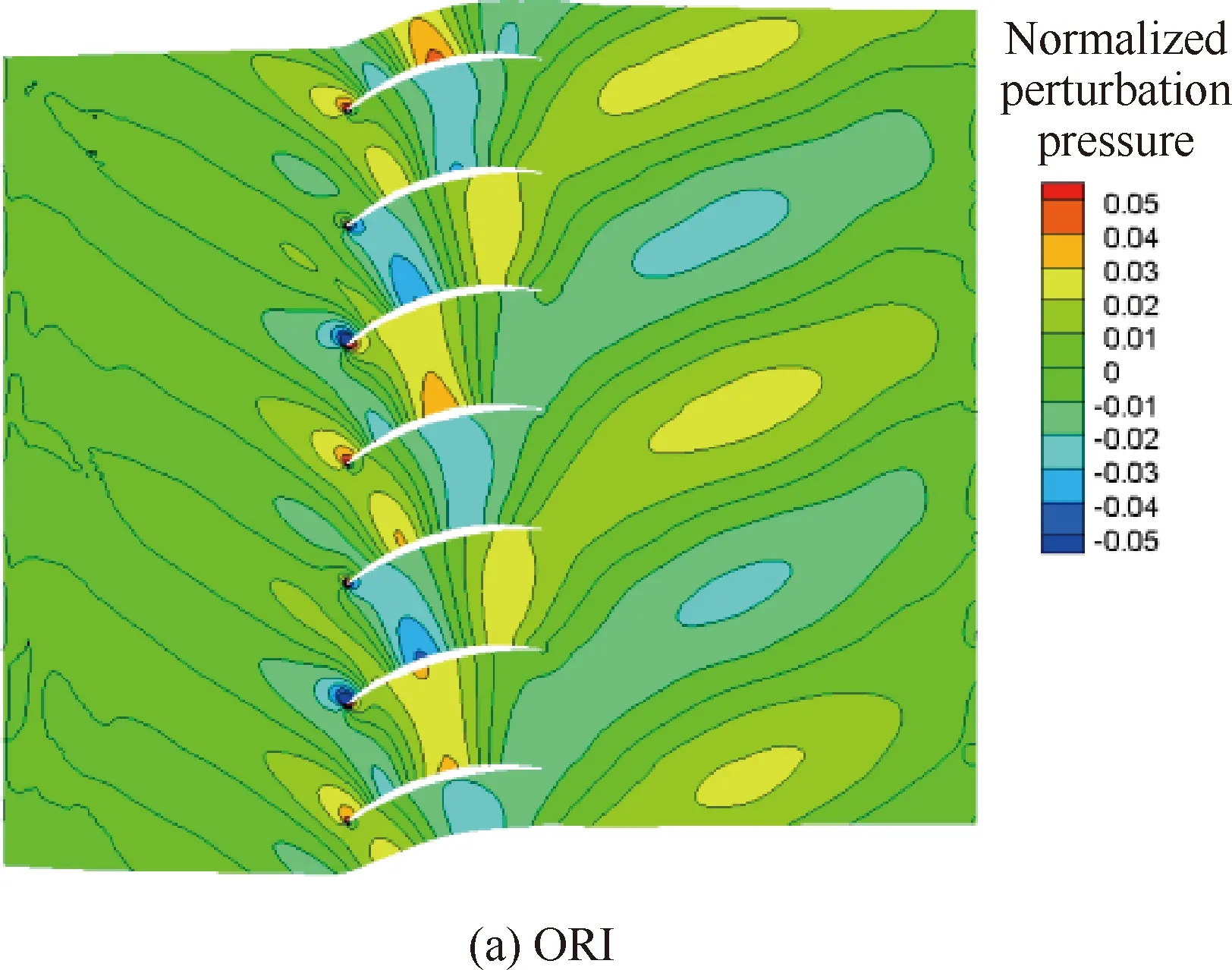
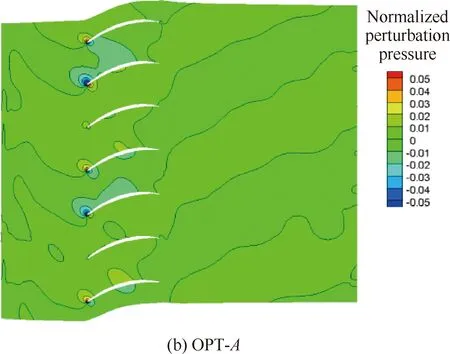
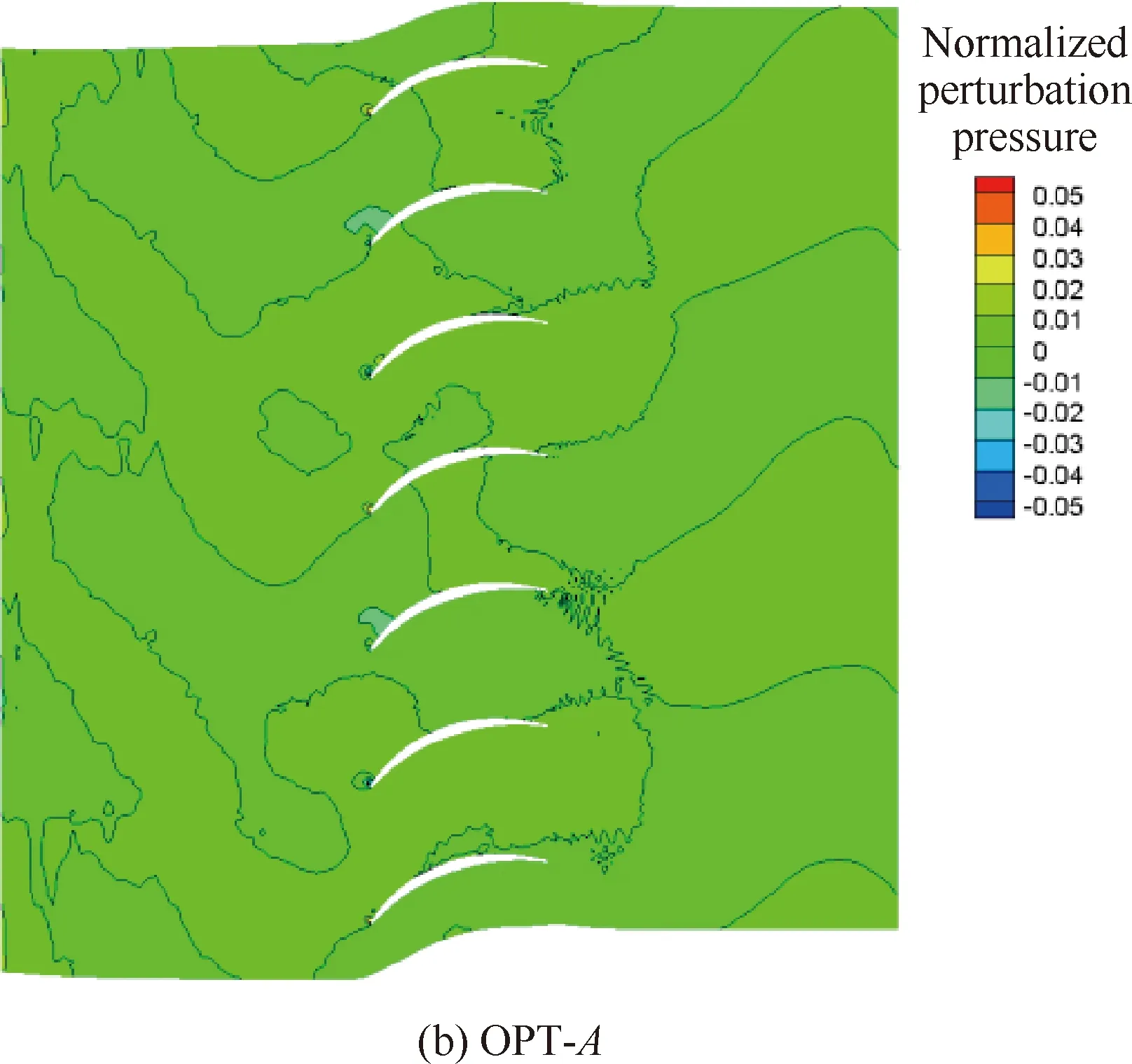
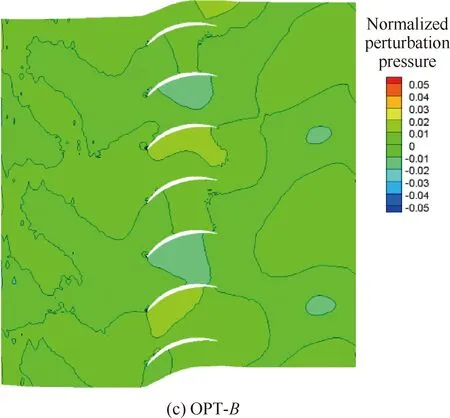
图10 OGV叶尖截面处无量纲脉动压力分布(设计状态)

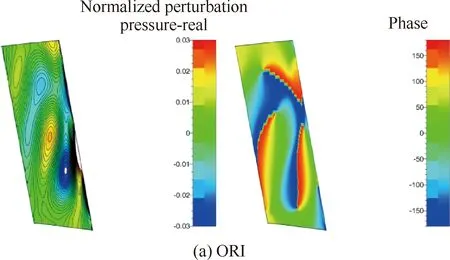
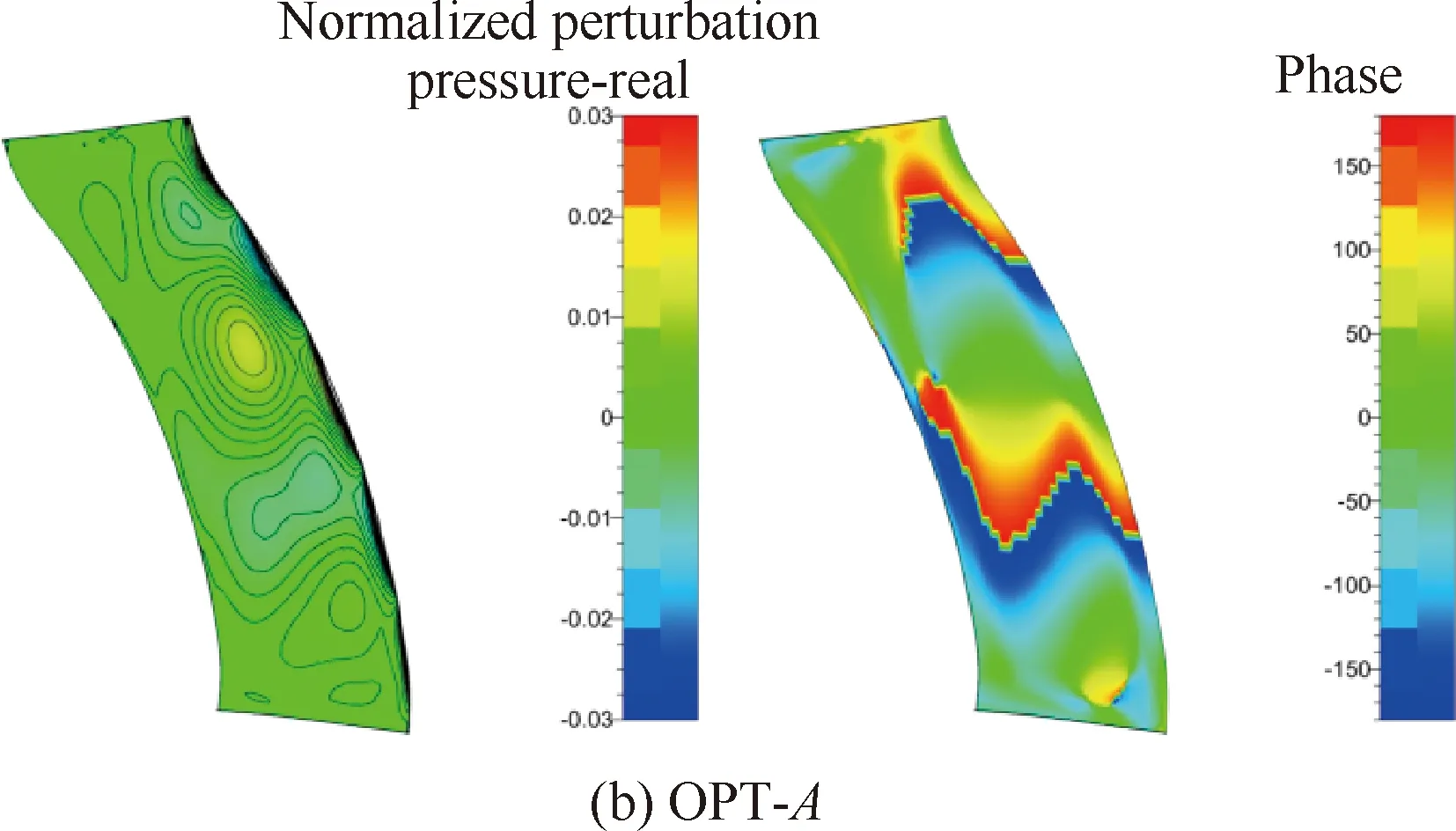
图11 OGV吸力面一阶无量纲脉动压力实部与相位分布(设计状态)

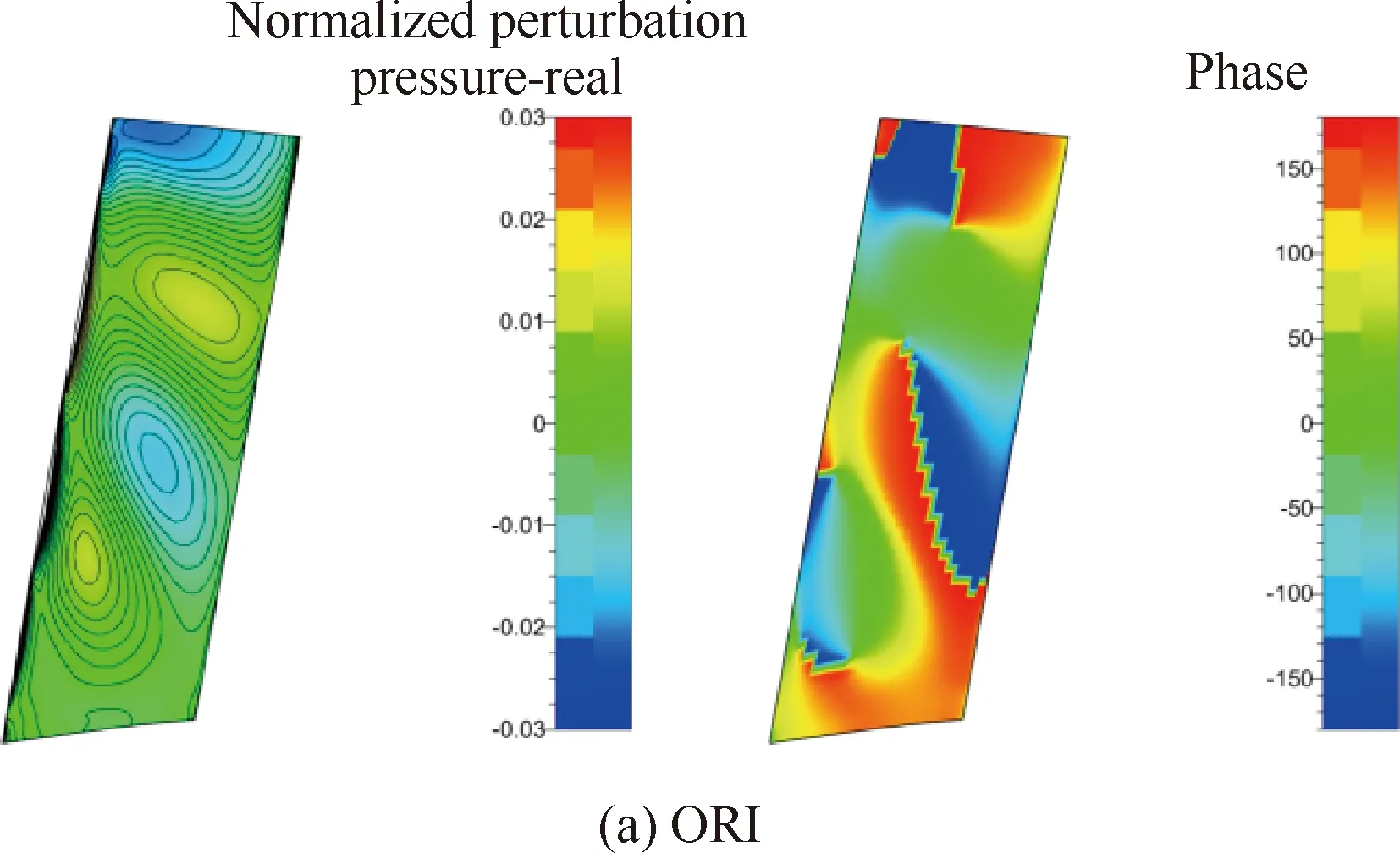
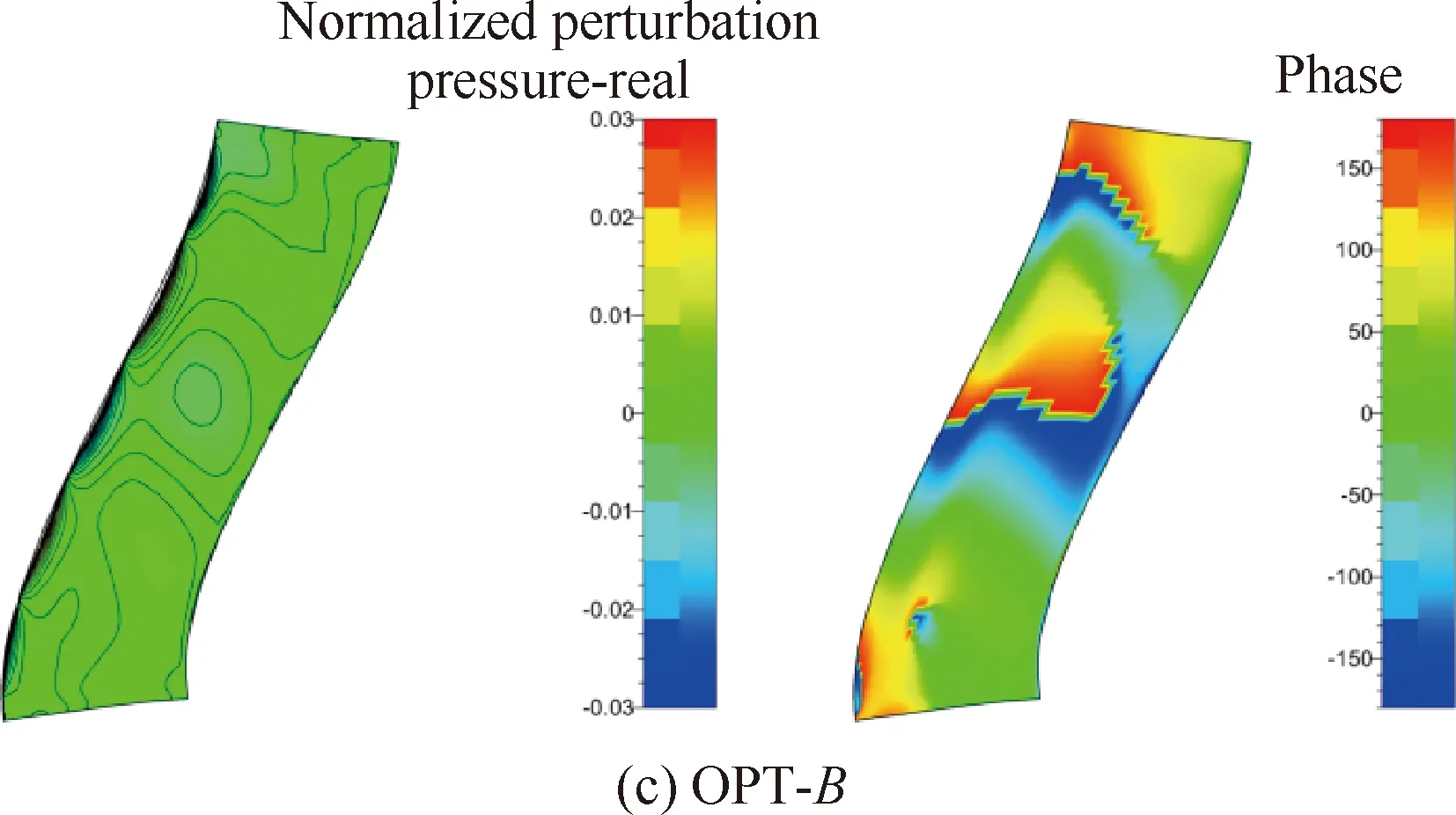
图12 OGV压力面上一阶无量纲脉动压力实部与相位分布(设计状态)

4 声模态分析

由于风扇/增压级试验件外涵流道近似平直管道，且OGV出口气流无旋，满足波分解方法使用条件，因而采用Wilson[16]提出的波分解方法对原型OGV及优化方案的噪声水平进行模态分析，并对降噪效果进行定量评估。波分解方法基本思想是将非定常流场表示成为模态叠加的形式，根据对特征值的分析，将其分别表示为向上游和下游传播的模态，同时准确区分压力主导的声模态和对流模态。波分解方法具体求解过程如下所述。

根据小扰动声波传播控制方程，圆柱坐标系下对流波动方程可写为

(5)

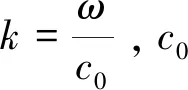
(6)

(7)

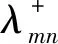
(8)

(9)

(10)

满足Bessel方程的式(8)的解可以写为

ψmn(r)=AJm(μmnr)+BYm(μmnr)

(11)

式中:Jm(x)和Ym(x)分别为第一类和第二类柱贝塞尔函数；A和B为方程待定系数。根据固体壁面边界条件，可求得相应的特征值μmn及待定系数A与B。这样一来，管道内的声压可以由式(6)表示为不同径向和周向管道模态的叠加，而该模态是否能在管道内传播则由管道内的流动条件和边界条件确定。

对于给定的频率、周向模态和径向模态，整个压力场写成2个声波解的叠加。

p=[p+(x)+p-(x)]ψmn(r)eiωt+mθ

(12)

对于无旋流中：

(13)

(14)

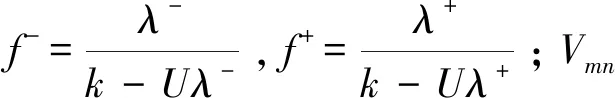
为了验证模态分析方法的正确性，按照图13(a)给定位置提取截面信息进行波分解，将分解得到的结果进行重构并与原始信号进行对比，如图13(b)～图13(d)所示。Z1截面位于风扇转子前，此截面处来流可认为是无旋流，除根部受流道收缩的影响误差较大外，其他位置重构信号与原始信号吻合较好；Z2截面位于风扇转子后、OGV前，此截面处存在较强的旋流，因此整体误差较大；Z3截面位于OGV后，可以看到重构信号与原始信号精确吻合，在此处气流流经OGV后旋流得到有效消除，而且流道近似等直径环管，与波分解方法的假设一致。综合上述信息，可以采用波分解方法对转子进口段、外涵OGV出口段进行模态分析。

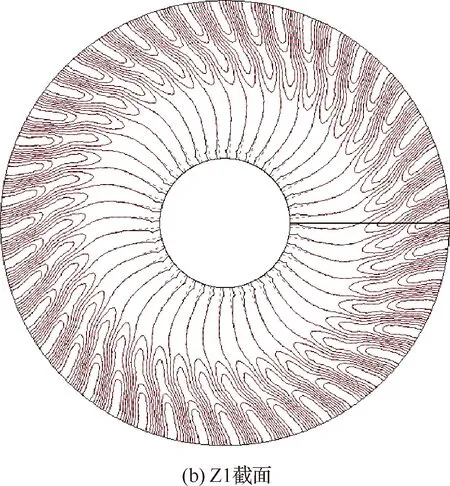
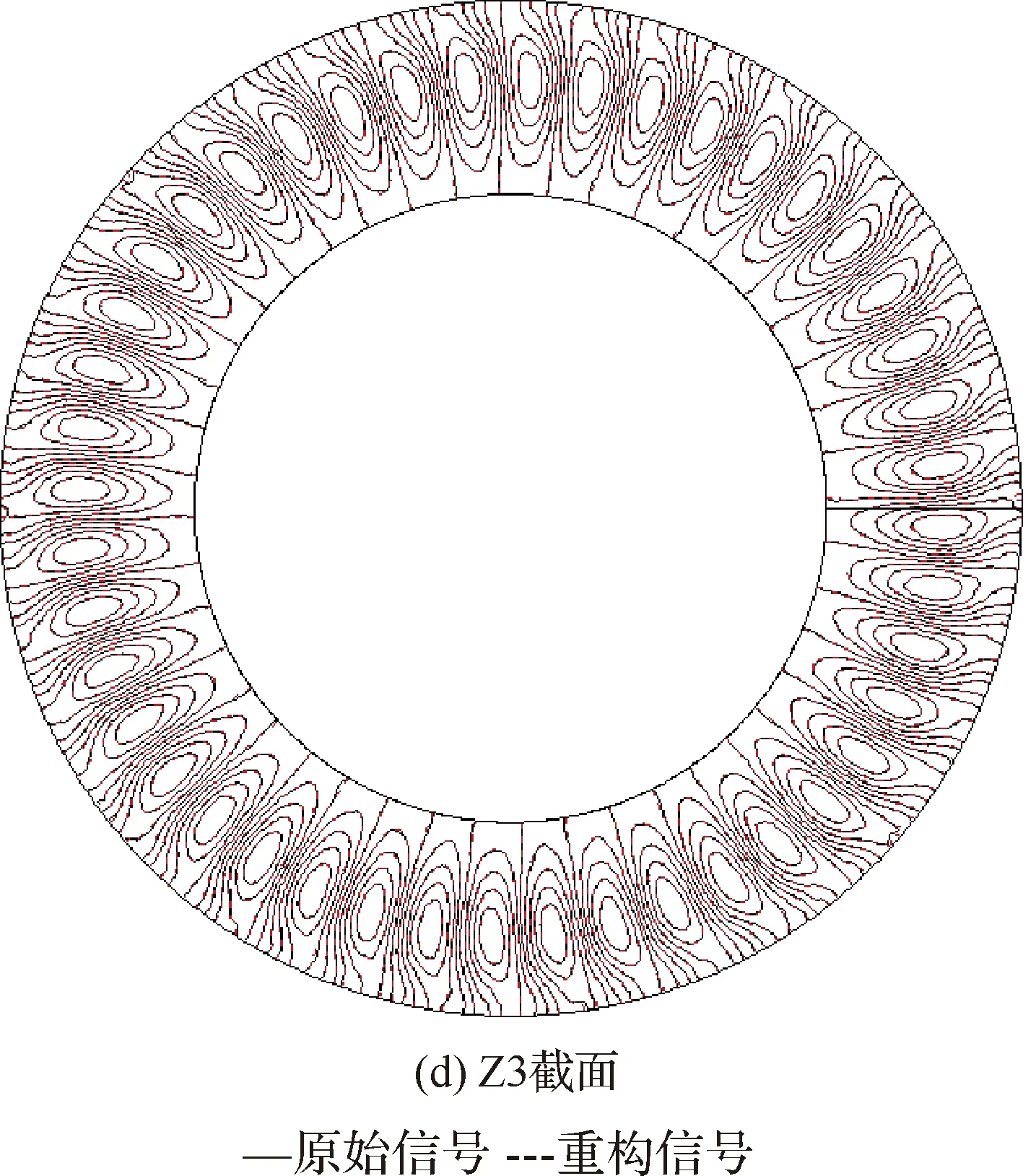
图13 不同截面处重构信号与原始信号对比

图14～图17给出了优化方案在风扇不同转速OGV后传声功率相对降噪量沿轴向的分布，对比分析低噪声优化OGV方案的降噪量。由于OGV后截面的前传噪声包含由数值模拟过程中出口边界造成的数值反射，后传噪声更能反映转/静干涉噪声水平，因此仅给出了后传噪声的相对降噪量。

图14 起飞状态OGV后传相对声功率沿轴向分布

从图14(a)中可以看出，在起飞状态1BPF下，OPT-A方案降噪量约4 dB，OPT-B方案降噪量约3 dB。图14(b)为起飞状态OGV后2BPF声功率的结果，此时OPT-A降噪量达到近9 dB，OPT-B方案降噪量达到约6 dB。图15给出了设计状态1BPF与2BPF的结果，在设计状态1BPF下，OPT-A方案降噪效果最好，为14 dB，OPT-B方案达到了8 dB左右，而针对2BPF的降噪量，OPT-A方案达到了10 dB，OPT-B为5 dB左右。本研究第1部分采用解析预测模型，对低噪声OGV进行评估，具体如图16所示：设计状态2BPF下，解析模型预测的OPT-A方案后传噪声降低8.8 dB，与波分解方法预测结果相差1.2 dB；预测的OPT-B方案后传噪声降低9.6 dB，与波分解方法预测结果相差4.6 dB。图17为爬升状态1BPF与2BPF的结果，可以看到，1BPF下OPT-A方案降噪量平均约为11 dB，OPT-B方案降噪量平均约为8 dB，2BPF下OPT-A方案降噪量平均约为10.5 dB，OPT-B方案降噪量平均约为9.5 dB。

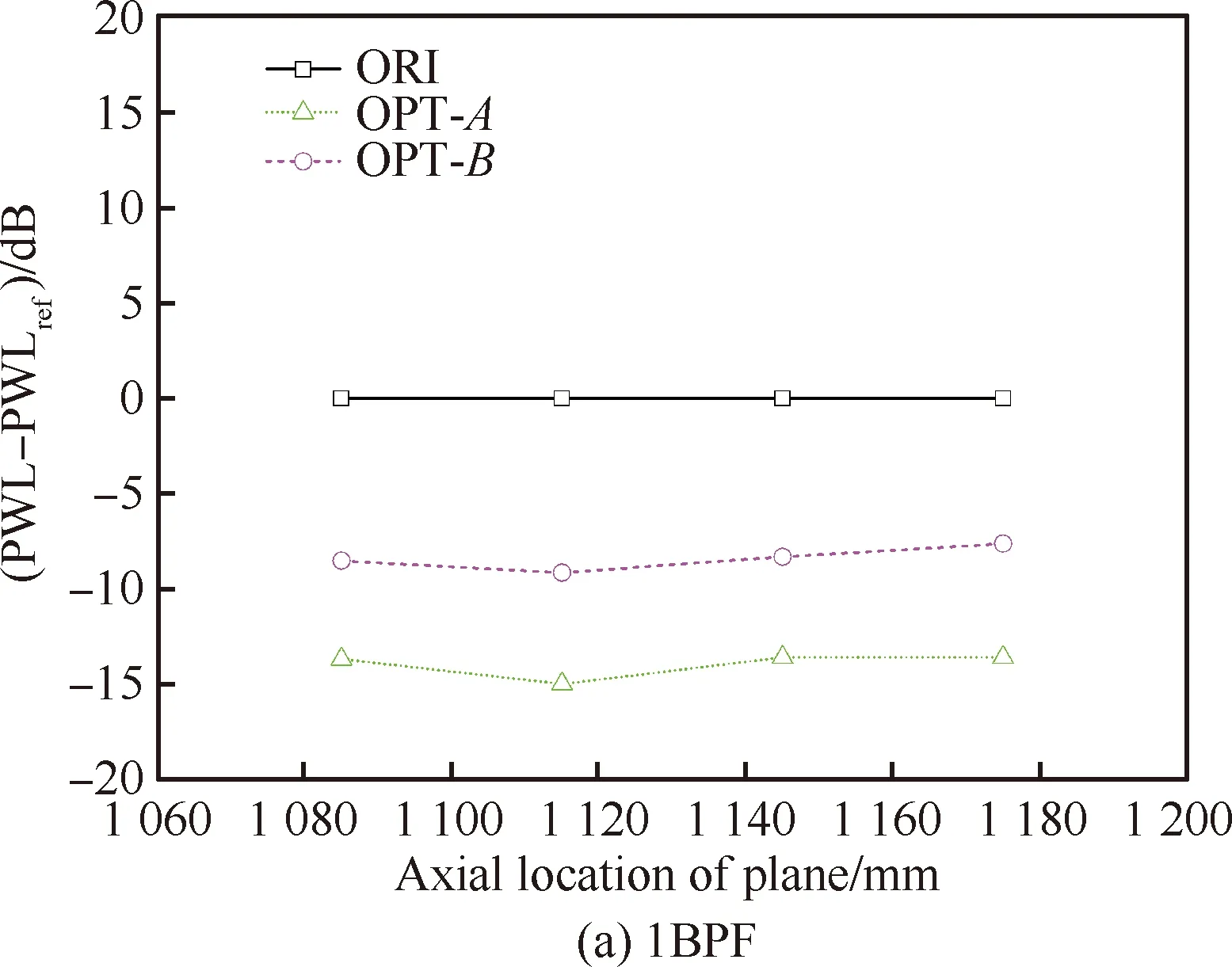
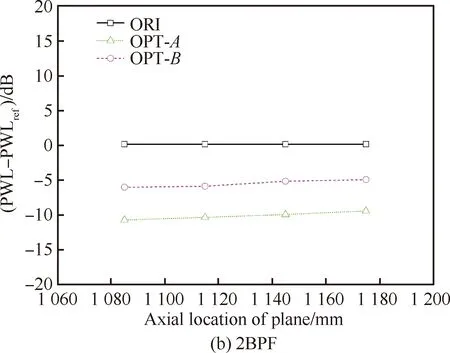
图15 设计状态OGV后传相对声功率沿轴向分布

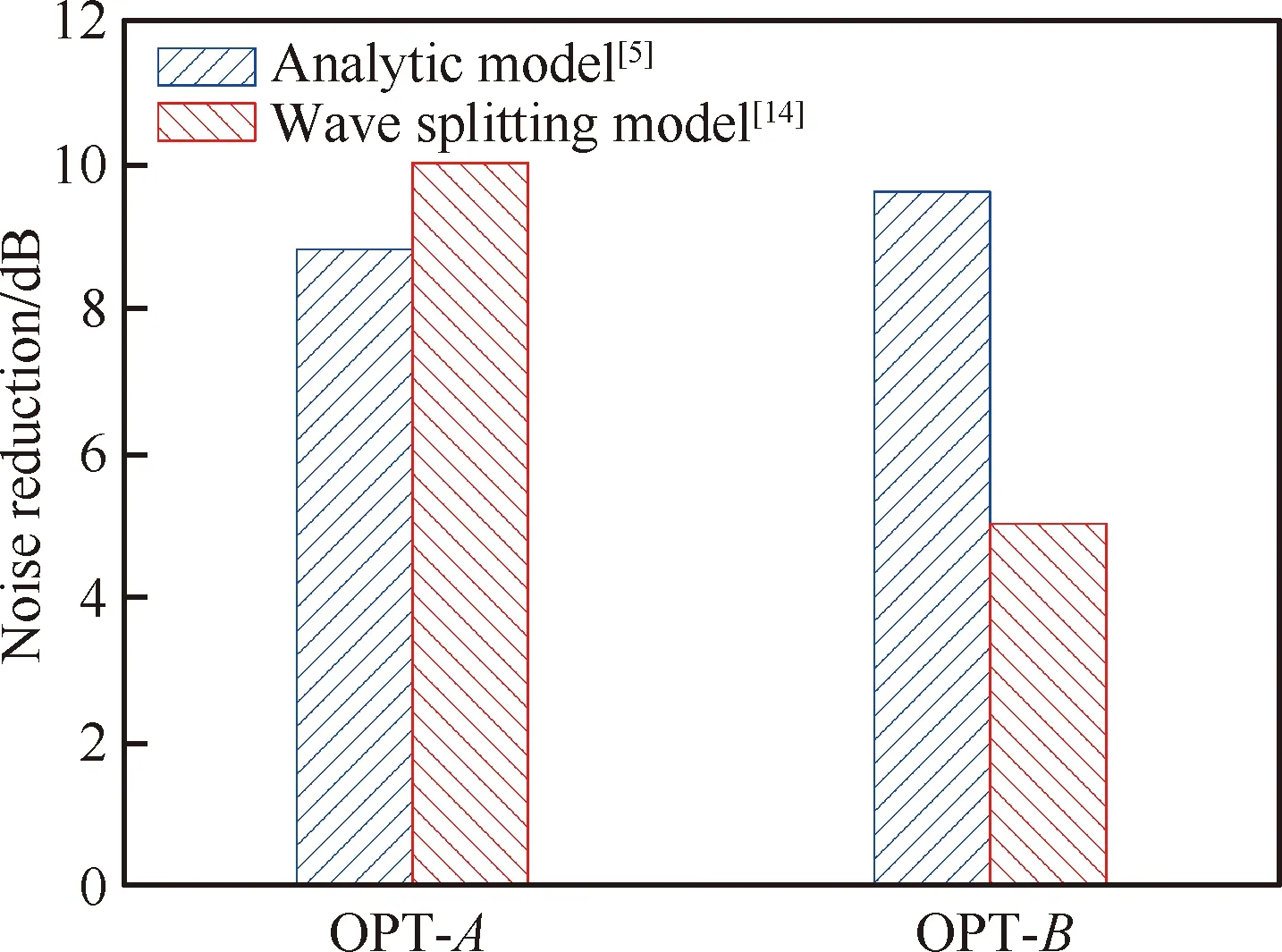
图16 解析预测模型[5]与波分解方法[14]预测2BPF降噪量对比

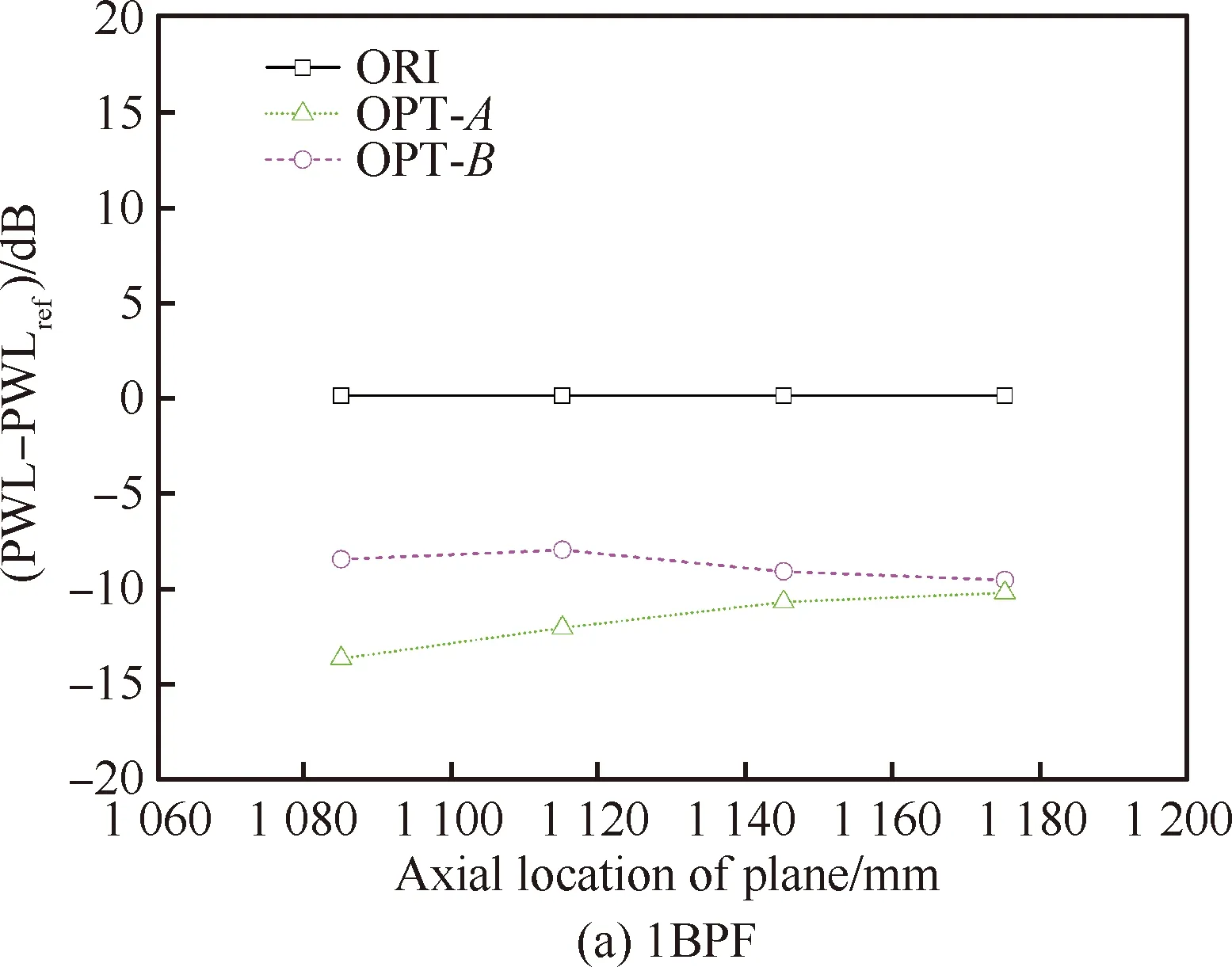
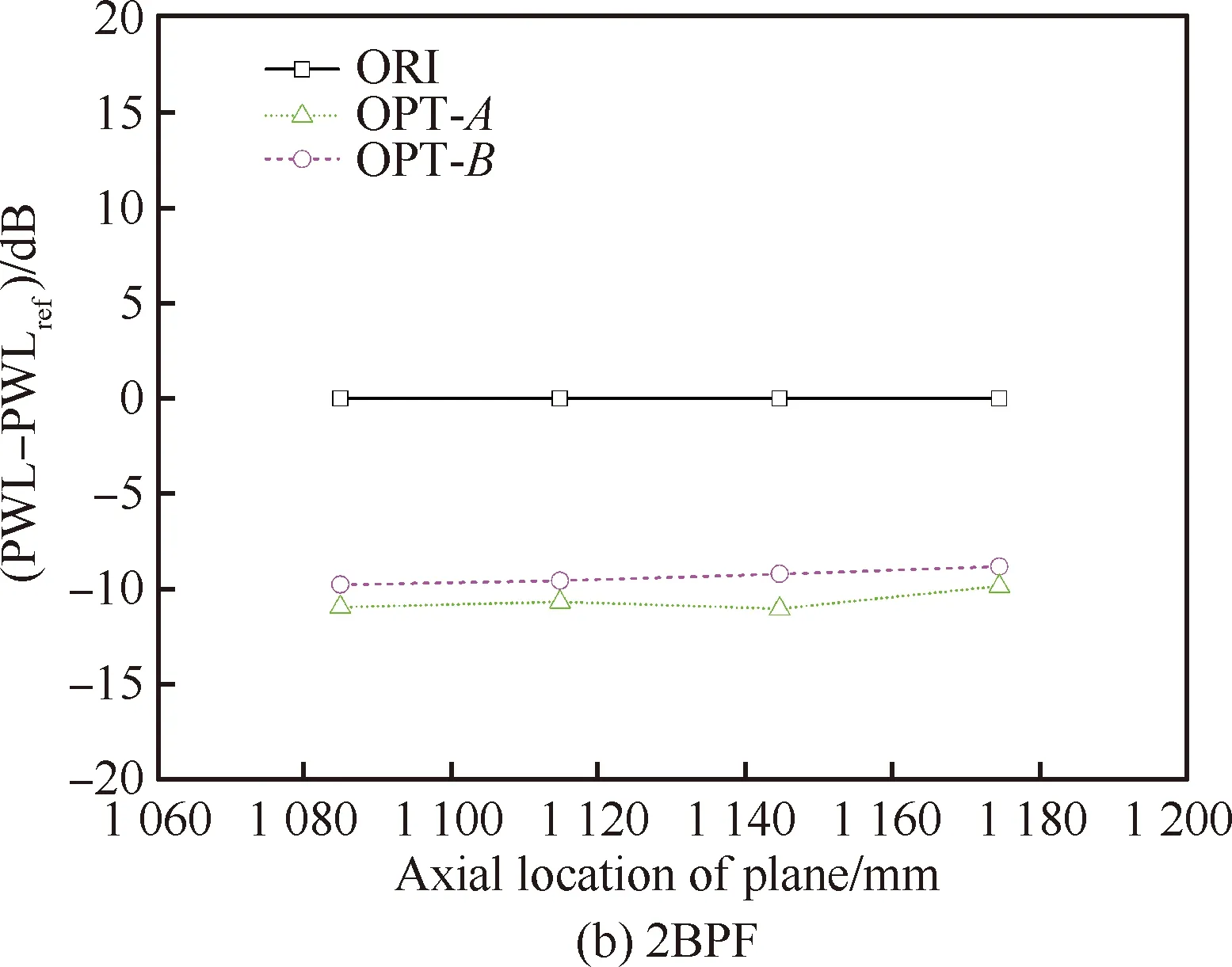
图17 爬升状态OGV后传相对声功率沿轴向分布

综合来说，两方案的降噪量除起飞状态的1BPF，均超过了5 dB，OPT-A方案在设计和爬升状态均为最大降噪量方案，均超过10 dB。

根据Tyler和Sofrin[20]的模态传播理论，压气机管道内的声模态满足公式m=sB+qV，B为转子叶片数22，V为静子叶片数70，s为BPF谐波数。表4给出了1BPF和2BPF时OGV后的转/静干涉噪声模态数，在起飞、设计和爬升状态，1BPF可传播的周向模态只有22，2BPF可传播的周向模态有-26和44。为了更清晰地展示模态声功率随状态的变化情况，图18给出了OGV后某截面3个主要模态。

由对应的声功率和相对降噪量，可以看出OPT-A方案在各转速1阶与2阶BPF的主模态降噪量均优于OPT-B方案，且降噪量并不随转速单调变化。

表4 转/静干涉模态m=sB+qV(B=22,V=70)

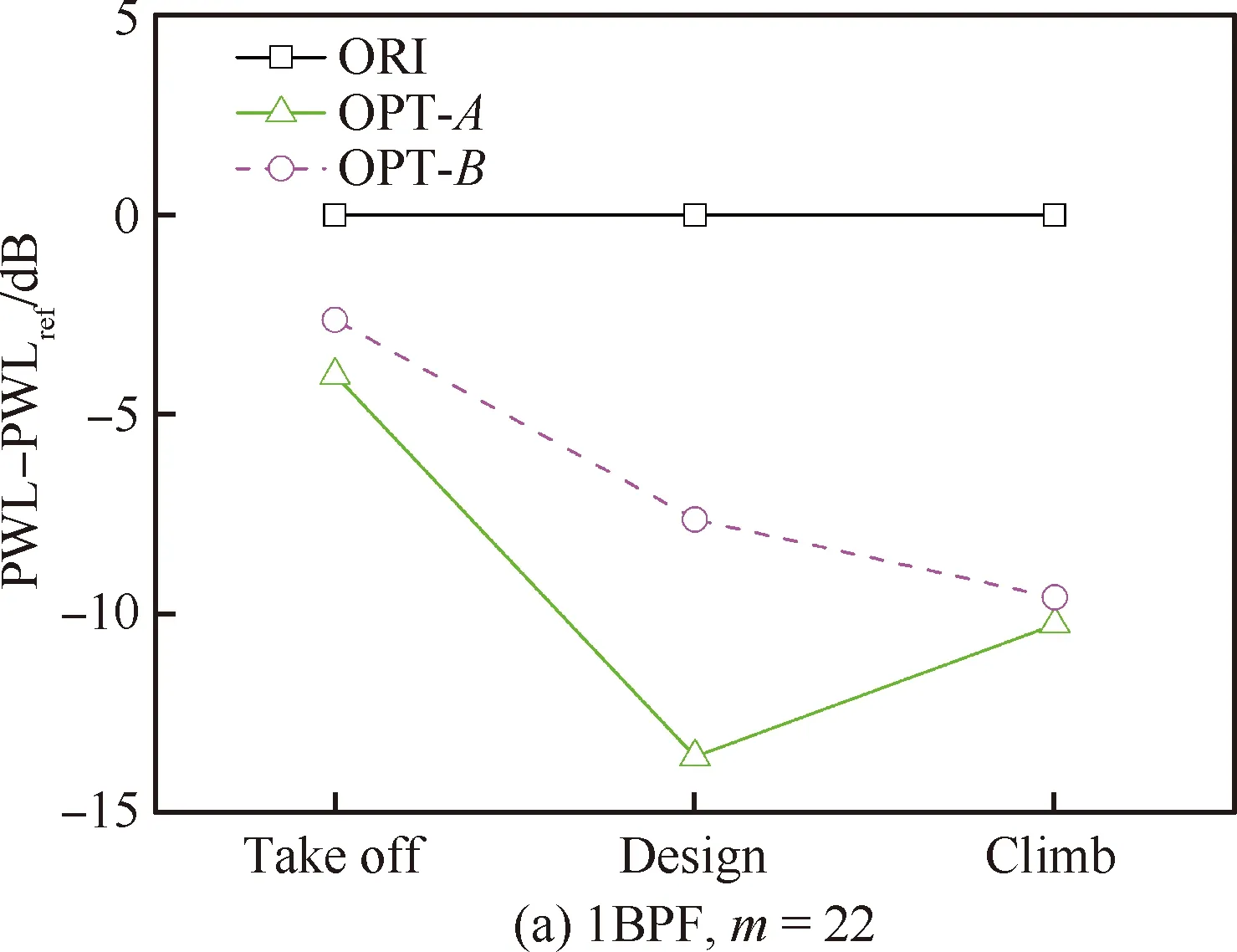
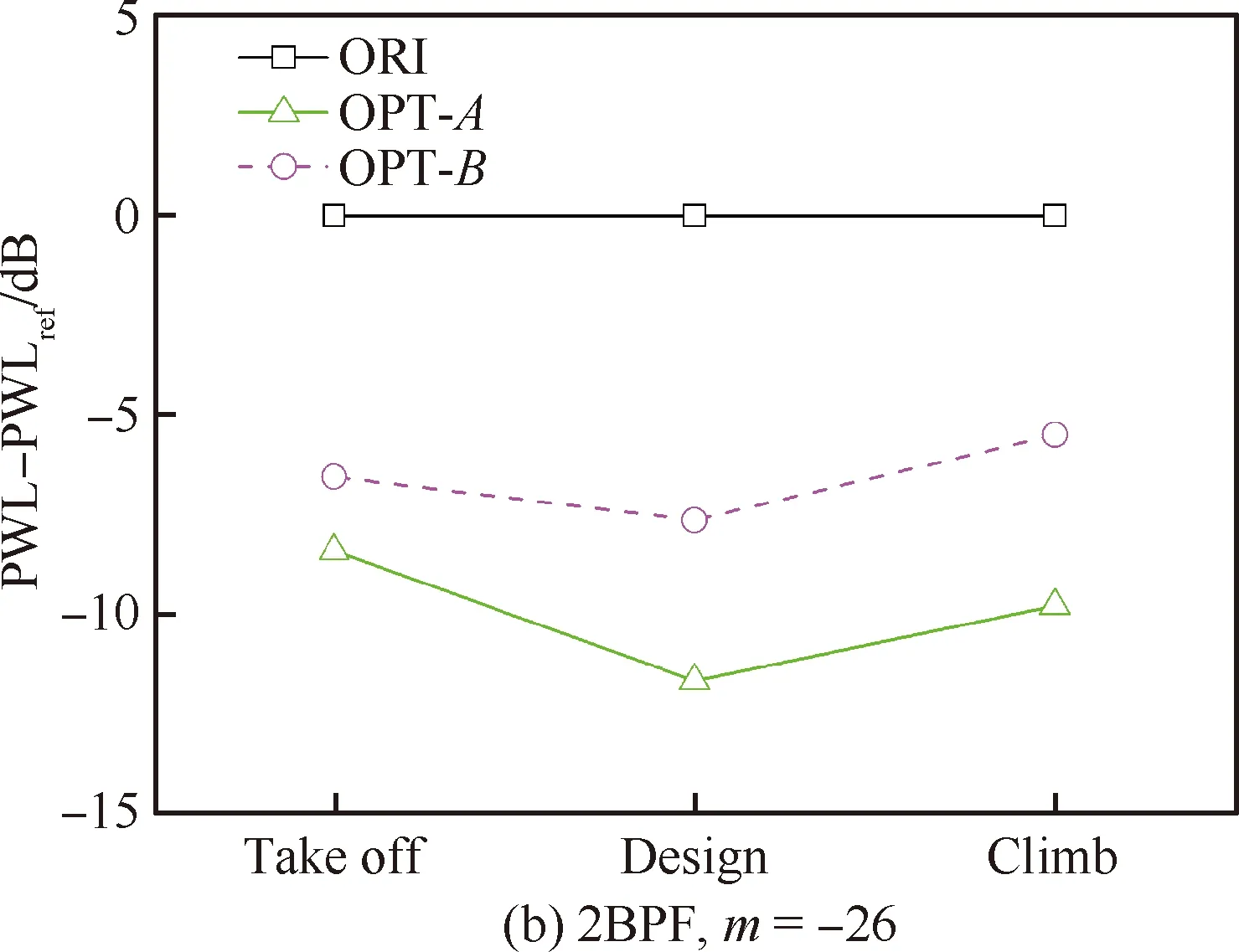
图18 相对声功率随状态的变化

5 结 论

本文使用非线性谐波法对OGV低噪声优化设计方案进行了详细分析，进一步确认了两方案的降噪效果。通过对OGV脉动压力分布的分析发现，经低噪声优化设计后，降低了OGV表面的非定常响应，槽道内的脉动压力明显减弱，由于轴向掠形和周向倾斜的有效组合改变了OGV表面脉动压力相位分布，沿径向的相位变化增加了相互抵消干涉的机会。最后，在基于波分解的模态分析方法基础上，对低噪声OGV方案相对于原设计的降噪量进行了量化评估，结果表明，除起飞状态1BPF降噪量为3 dB左右外，其余状态均超过了5 dB。