聚丙烯加捻绳与编织绳拉伸力学性能对比研究

2019-10-28曹宇光徐国强

中国塑料 2019年10期

张磊，曹宇光，宋明，徐国强

(中国石油大学(华东)储运与建筑工程学院工程力学系，山东省油气储运安全重点试验室,山东青岛 266580)

0 前言

近些年来，聚丙烯纤维复合材料以高强、抗冲击、耐磨、耐腐蚀和力学性能优良越来越受到国内外的关注[1]。聚丙烯绳存在弹性模量低、载荷作用下变形较大等问题，限制其广泛应用[2]。绳按加工结构分为加捻绳和编织绳[3]两类，其中加捻绳由每丝加捻成绳股，多股再加捻成绳。受加捻工艺和自身结构的影响，当对该类绳施加拉力作用时会产生以其轴为中心的旋转，并且随着绳长度的加长，其旋转的角度会越来越大；编织绳是由每丝加捻成绳股，多股再一组右向编织和一组左向编织呈有规律的编织而成。其中左、右向编织股数量相等且对称，两组绳股产生的螺旋力矩因方向相反而平衡。当对该类绳施加拉力作用时绳的旋转角度、合成转矩等于零，编织绳克服了加捻绳的旋转问题[4]。虽然不同结构绳广泛应用，但两种结构绳的应力对结构的影响仍存在不足[5]。本文以聚丙烯绳为研究对象，进行准静态拉伸测试[6]，得出两种结构绳的本构关系及力学参数。通过SolidWorks建立绳的实体模型，导入ANSYS软件进行分析计算[7]。比较实验结果和有限元模拟关联结果，验证模型的合理性。通过变形、应力分布规律等[8]情况对比两种绳的破坏行为，为绳的可靠性设计与合理选用提供依据。

1 实验部分

1.1 主要原料

直径28 mm 3股聚丙烯加捻绳、直径40 mm 8股聚丙烯编织绳，扬州力达绳缆科技有限公司。

1.2 主要设备及仪器

微机控制电子万能试验机，CTM9100，协强仪器制造(上海)有限公司；

非接触全场应变测试系统，VIC-3D，美国CSI公司；

数码单反相机，尼康D7200, 尼康映像仪器销售(中国)有限公司。

1.3 样品制备

两种试验样品参数分别为：(a) 加捻绳：8捻/220 mm，(b) 编织绳：3个花节/220 mm，试验样品如图1所示。

(a)加捻绳 (b)编织绳图1 实验样品示意图Fig.1 Schematic diagram of the test sample

1.4 性能测试与结构表征

(a)加捻绳 (b)编织绳图2 拉伸示意图Fig.2 Schematic diagram of stretching

采用电子万能试验机按GB/T 1147—2005[9]，在室温干态的测试环境下对聚丙烯样品进行力学性能测试，对不同直径的绳采用不同形式的夹具，如图2所示；其中加载速率为以20 mm/min的速度在下夹具端施加轴向拉伸载荷；实验过程中采用的两种试验夹具均尽可能减少偏心拉伸造成的试验误差；通过试验机控制软件设置拉伸方式、预紧力，输入缆绳的原始尺寸、试件长度，加载方式为单步加载；直至下夹具达到到试验机最大量程，停止试验，并自动输出试验数据；

采用VIC-3D非接触全场应变测试系统，拍摄两种结构绳的绳股破断过程，如图3所示；采用尼康D7200数码单反相机，拍摄破坏断口形貌，如图4所示。

图3 绳股破断过程Fig.3 Breaking process of cable strands

(a)外层破断时断口 (b) 内层破断时断口图4 绳股断口形貌Fig.4 Fracture morphology of cable strands

2 结果与讨论

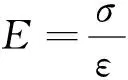
表1 聚丙烯绳的实验参数

Tab.1 The experimental parameters of polypropylene cables

1—加捻绳 2—编织绳图5 加捻绳与编织绳的载荷 - 位移曲线对比Fig.5 Comparison of load-displacement curves between the twisted cables and plaited ones

由图3可知，加捻绳股在受到轴向拉力作用下，绳股由外层向内层逐层破断。由图4可知，绳股外层破断时断口平整，外层破断后，内层不足以承受最大载荷继续伸长变形，达到塑性阶段最终破断，断口毛糙。由图5可知，加捻绳在拉伸位移约为110 mm时载荷迅速下降，是由于每股绳具有相同的加捻角度，绳股共同抵抗载荷，同时达到断裂极限，但仍有部分股继续承载，曲线又继续上升；编织绳未出现载荷急剧向下波动，但出现小锯齿的波动，说明部分绳丝已经开始断裂。在达到断裂极限之前绳逐步断裂直至不能承受最大荷重[10]。

由图5可知，拉伸初始模量[11]大小表示纤维在小载荷作用下变形的难易程度，反应绳的刚性。拉伸初始模量大，表示结构不容易变形，刚性比较好。反之，初始模量小，刚性比较差。通过观察曲线斜率得到加捻绳的拉伸初始模量高于编织绳，表明加捻绳的刚性好于编织绳，即编织绳质地较软。

3 不同结构聚丙烯绳的数值模拟

3.1 有限元计算模型

为了进一步研究聚丙烯绳结构的拉伸力学行为，了解其变形规律、内部的应力分布及其对破坏行为造成的影响。依据试件的几何特征，忽略绳股与每丝之间接触摩擦的影响，对绳模型进行了合理简化，通过SolidWorks建立实体模型。加捻绳建立3×7的几何模型，如图6(a)所示。编织绳通过Matlab软件得到曲线方程式建立其数学模型，得到每股的曲率。通过设置空间曲线参数方程于SolidWorks中，对生成的曲线进行扫描建立几何模型，如下图6(b)所示。结合拉伸试验得到两种结构绳的力学性能参数，如表2所示，及两种结构的整体本构关系进行有限元模拟。

(a)加捻绳有限元模型 (b)编织绳有限元模型图6 有限元模型Fig. 6 The finite element model

Tab.2 Mechanical properties of two kinds of cable structures

模型采用高阶的三维20节点结构的实体单元SOLID186，模拟完全不可压缩的超弹材料变形[12]。采用Sweep的方式进行划分网格，为了保证计算的收敛性，网格之间节点共用。模型一端施加全约束，另一端施加轴向位移；选择Full法Transient进行加载；在0.1 s内设置50个载荷步；通过Ramped Loading模拟准静态过程；开启Large Displacement Transient，对绳进行有限元分析。

3.2 模型准确性验证

■—加捻绳实验 ●—数值模拟图7 加捻绳实验与数值模拟载荷 - 位移曲线对比Fig.7 Comparison of tensile test and numerically simulated load-displacement curve of twisted cables

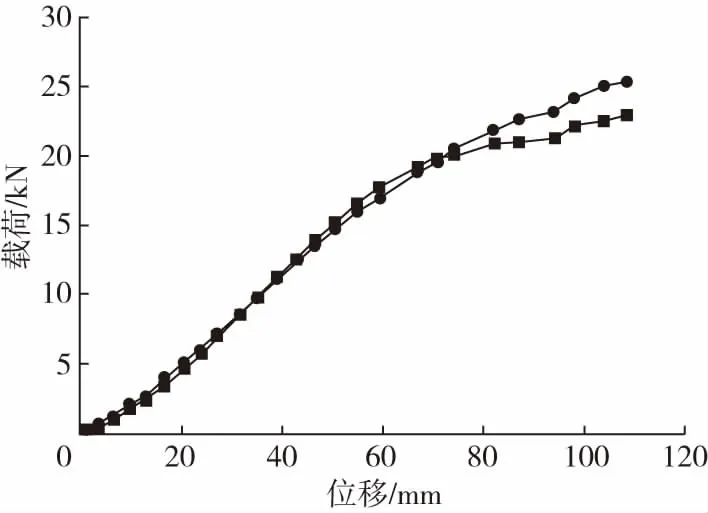
■—编织绳实验 ●—数值模拟图8 编织绳实验与数值模拟载荷 - 位移曲线对比Fig.8 Comparison of tensile test and numerically simulated load-displacement curve of plaited cables

通过ANSYS分析软件计算得到两种结构绳的载荷 - 位移曲线，与实验得到的载荷 - 位移曲线对比分析。如图7、图8所示，实验的载荷 - 位移曲线与数值模拟的载荷 - 位移曲线在弹性阶段吻合程度较好，具有相同的近似线性增长趋势。其中加捻绳模型与试验误差约为9 %。编织绳模型与试验误差约为13.7 %。

(a)加捻绳 (b)编织绳图9 变形云图对比分析Fig.9 Contrastive analysis of deformation

表3 两种结构绳的伸长率对比

Tab.3 Comparison of elongation at break of two structures of cables

综上：在误差允许范围内，通过载荷 - 位移曲线与伸长率的数值模拟结果与实验结果吻合验证加捻绳与编织绳的有限元模型简化合理。能够有效的研究绳拉伸破断过程的宏、细观破断过程，但模型简化仍存在问题，需要进一步简化。

3.3 结果对比分析

为研究不同结构绳受拉过程的力学性能，通过有限元软件ANSYS得到加捻绳与编织绳在轴向拉伸作用下的等效应力云图、轴向应力云图、切应力云图如图10、图11所示。如图10所示，加捻绳每股等效应力分布均匀，绳股共同承载直到达到按强度极限后破断。编织绳受力分散，在交叉编织处等效应力集中，绳股之间相互作用明显。如图11所示，两种结构绳在拉伸过程中受到轴应力与剪应力共同作用，但轴向应力远大于剪应力，等效应力的数值小于轴向应力的数值，说明轴向应力和剪应力的叠加作用使整体的等效应力减小。

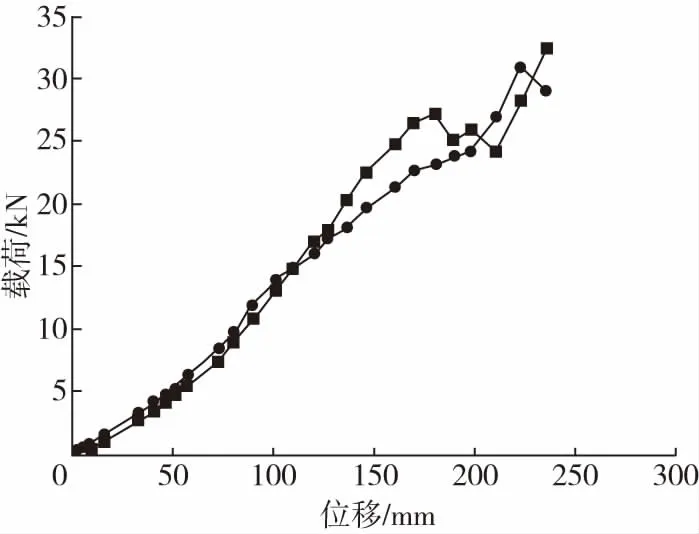
(a)加捻绳 (b)编织绳图10 等效应力云图对比分析Fig.10 Contrastive analysis of Von Mises stress

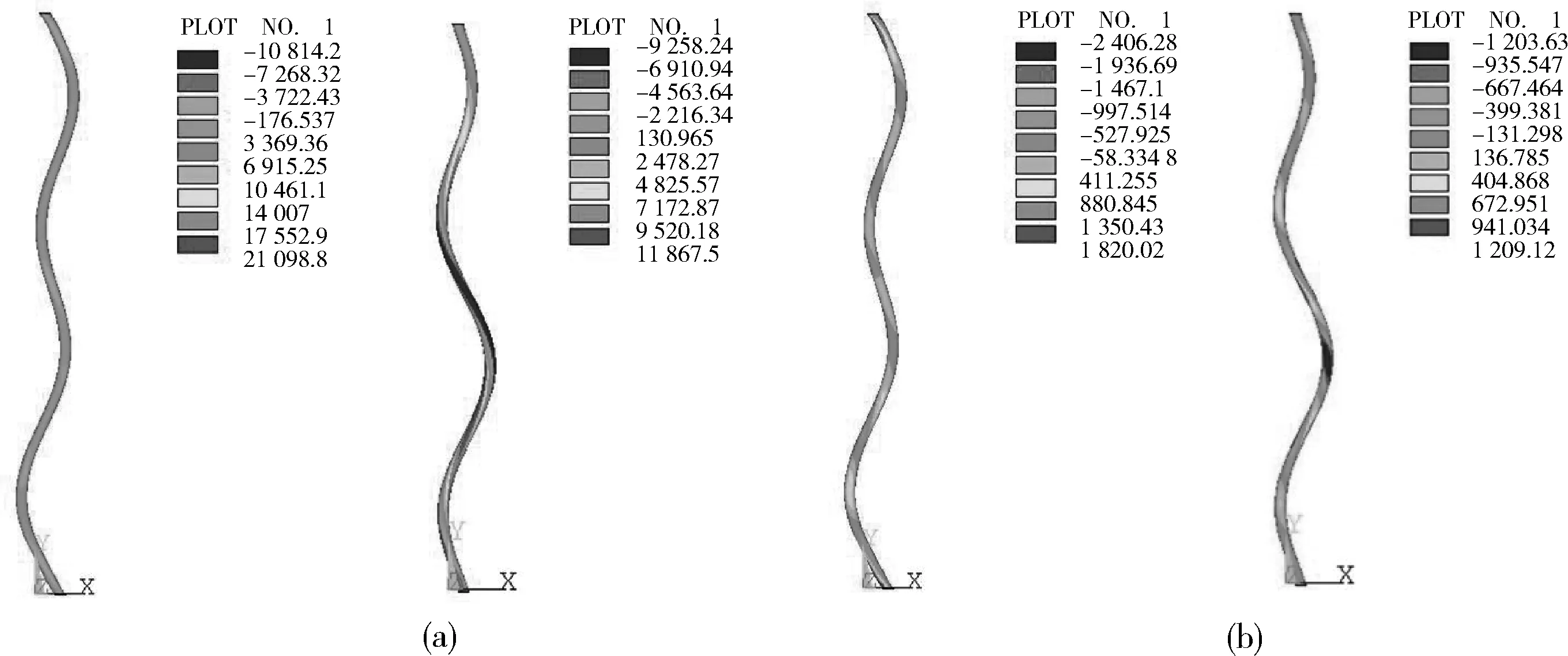
(a)加捻绳轴向应力 (b)编织绳轴向应力 (c)加捻绳剪应力 (d)编织绳剪应力图11 轴向应力、横截面剪应力云图对比分析Fig.11 Contrastive analysis of axial stress and shear stress

1—第一丝 2—第二丝 3—第三丝(a)加捻绳截面等效应力 (b)加捻绳沿周向等效应力分布曲线图12 加捻绳约束端截面沿周向等效应力分布Fig.12 Distribution of Von Mises stress along circumferential distribution of restraint end section of twisted cables

1—第一股 2—第二股 3—第三股 4—第四股(a)编织绳截面等效应力 (b)编织绳沿周向等效应力分布曲线图13 编织绳约束端截面沿周向等效应力分布Fig.13 Distribution of Von Mises stress along circumferential distribution of restraint end section of plaited cables

如图12所示，加捻绳截面应力以截面为中心向外周呈对称分布。如图13所示，编织绳截面等效应力呈交错分布。位于纵向的等效应力明显小于横向的等效应力，但两种结构绳应力呈层状分布，应力值由每股截面中心向外周逐渐增大。

对比图12(b)、图13(b)周向等效应力分布曲线，加捻绳截面外周等效应力明显大于中心等效应力，因此，破断时从外侧逐层向内层断裂。符合实验过程中出现的在加捻绳外侧逐层向内断裂的实验现象。编织绳其中4股纵向的应力较小明显小于另外4股横向的应力。拉力达到断裂极限后，应力较大的4股断裂，另外应力较小的4股继续承受载荷。

为通过数值模拟对试验得到的绳索破断后断口形貌进行合理解释，对绳股提取外、内丝的轴向应力与剪应力观察受力特点，如图14所示。

如图14所示，绳股的外丝轴向应力大于内丝接近2倍，远大于绳股外丝剪应力，此时外丝轴向应力是绳股破断的主要因素，此时为单向应力状态，如图3及4(a)所示绳股外层先断裂且断口形貌整齐；绳股的内丝继续承载破断载荷使聚丙纶绳丝经过屈服阶段达到塑性阶段，但此时轴向应力变化明显，剪应力变化幅度较小，此时绳股内层破断是由于轴向应力与剪应力及摩擦力共同作用的原因，此时为二向应力状态，如图3及4(b)所示破断处发生塑性变形且断口毛糙。