一种面向中小规模数据集的模糊分类方法∗

周 塔 , 邓赵红 , 蒋亦樟 , 王士同

1(江南大学 数字媒体学院,江苏 无锡 214122)

2(江苏科技大学 电子信息学院,江苏 张家港 215600)

模糊系统作为智能计算领域的一个及其重要的研究分支,由于其自身较强的可解释性和学习能力而被广泛地应用到多个领域[1,2].Takagi-Sugeuo-Kang(TSK)模糊系统由于其输出的简洁性,其训练过程通常可以转化为二次规划问题或者线性回归问题进行求解,这就使得TSK模型比其他模型训练过程更迅捷、更高效.同时,因其较好的逼近性能而被应用到多个领域,比如模式识别、图像处理和数据挖掘等[3,4].模糊系统是根据模糊集和模糊推理理论而形成的智能系统,它主要是把自然界的模糊语言向模糊规则进行转换.正是凭借这一特性,模糊系统在日常生活中仍被广泛使用.目前,已经建立或者识别的TSK模糊分类器大致可分为以下几种:基于遗传算法的TSK模糊分类器、基于神经-模糊混合的TSK模糊分类器和类似层次状的TSK模糊分类器.对于遗传算法的TSK模糊分类器而言,它主要是模仿人类的进化过程去构造结构和识别参数.典型工作包括基于TSK模糊分类器的多目标遗传算法,该算法将规则选择问题转化为多目标的组合优化问题.对于神经-模糊混合的TSK模糊分类器,它主要是把人工神经网络和模糊系统进行组合.典型的工作包括基于TSK模糊分类器的BP神经网络,这类工作主要是通过BP神经网络和BP算法混合而成,用来训练分类器和SVM的相关参数.这类的工作可以参考文献[1,5−8].而对于类似层次状的TSK模糊分类器,主要包括具有层次模糊系统和具有全局逼近性能的模糊系统.关于这类算法及其改进算法可以参考文献[9−15].这3类TSK模糊分类器都不可避免地遇到这样的挑战:(1) 当输入的样本维数过高时,会出现维数灾难;(2) 在TSK模糊系统中,不恰当的模糊划分在某种程度上也会影响模糊规则意义的表达;(3) 训练完模糊系统后的修整技术在某种程度上会去除一些不合理的模糊划分,但是这种后续处理方法势必也影响了分类的精度.

我们所提出的模糊分类器RCC-DTSK-C类似于层次状的TSK模糊分类器,但是有本质的区别,它能有效地避免TSK模糊分类器所面临的巨大挑战.这一点在文后有详细的报道.

深度学习理论已经成为当前研究的热点,它在很多领域都取得了成功[16−27].我们知道,深度结构能够快速而有效地捕获源数据中的细节,而恰好这些细节有时候却能更好地表达可解释性.

本文利用栈式结构[28]构造深度TSK模糊分类器来学习模糊规则,以提高分类性能.深度结构能够估算TSK模糊分类器的预测误差,栈式结构可以帮助我们解决困难的非凸优化问题,而这些问题也正是深度学习要解决的.

本文基于以下几种考虑构造了可解释性很强的TSK模糊分类器.

(1) 模糊划分数不确定,完全随机生成,比如随机生成3个模糊划分,对应高斯隶属函数中心点为[0,0.5,1],其语义表示为{差,中等,好};再如随机生成5个模糊划分,对应高斯隶属函数中心点为[0,0.25,0.5,0.75,1],其语义表示为{很差,差,中等,好,非常好};

(2) 随机选取源数据集中的部分或者大部分特征数据;

(3) 每个基训练单元中的模糊分类器拥有相同的输入空间;

(4) 由于0阶TSK模糊分类器的输出结果是常数,对于系统易于分析和表达,本文将以0阶TSK模糊系统为基础训练模型,探讨随机模糊划分和规则组合的深度0阶TSK模糊系统的建模方法.

1 Takagi-Sugeno-Kang模糊系统

1.1 经典TSK模糊系统

根据文献[1],经典模糊系统主要有Takagi-Sugeno-Kang模糊系统(TSK-FS)、Mamdani-Larsen模糊系统(ML-FS)[1]和广义模糊系统(GFM)[1]这3种.对于经典TSK-FS而言,其模糊规则表示为

这里,x=[x1,x2,…,xd]T为输入向量,表示第i个输入变量xi所对应的第k条规则描述的模糊子集,K代表模糊规则数.每条规则都与x相对应,同时把输入空间的模糊子集Ak∈Rd映射到输出空间的模糊子集fk(x),其中,Ak表示为则为模糊子集fk(x)相对应的隶属函数.那么第k条规则隶属函数uk(x)表示为

在反模糊化之前,若采用重心反模糊化操作,则最终的输出f(x)即可描述为

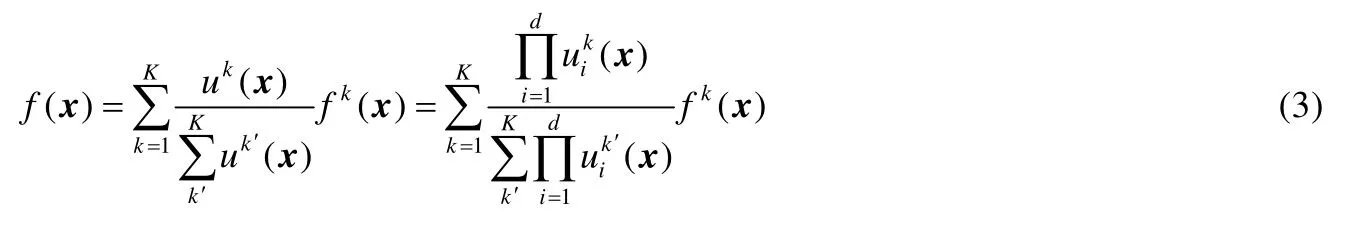
经典模糊系统模型可以分为TSK模糊系统、ML模糊系统和GFM模糊系统.对于ML模糊系统,其模糊规则表示为

对于GFM模糊系统,其模糊规则表示为

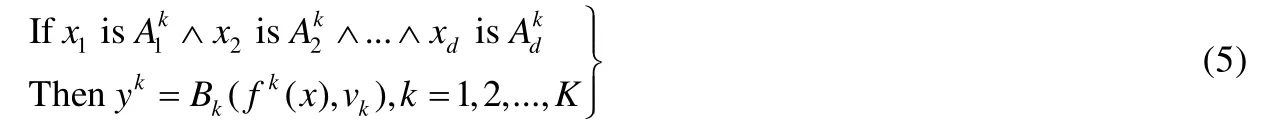
其中,Bk(⋅)表示ML模型中第k条模糊规则对应的模糊集,bk和vk分别称为质心和模糊系数.

1.2 0阶和1阶TSK模糊分类器

在公式(11)和公式(12)中,ujk表示为xj=(xj1,xj2,…,xjd)T隶属于第k类的隶属程度.这里,h为尺度参数,该尺度参数可以人为地调节.

根据文献[30],有:

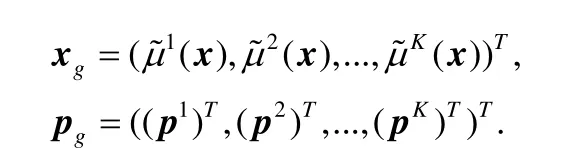
即0阶TSK的输出y0则可表示为

以上描述可参见文献[2].由此可知,模糊规则假设的参数确定后,模糊规则的参数学习问题可转化为线性回归问题[1,31]来求解.这就使得在系统建模时,用线性回归模型替代TSK来进行处理.

通常情况下,0阶TSK模糊分类器的分类性能比1阶TSK差.但是1阶TSK模糊分类器很难对每条模糊规则下的(d+1)参数给出清晰的解释.当每条规则下仅有1个参数,那么的正负值就很容易解释为属于或者不属于第k类的度值[30].本文提出深度结构的目的就是提高分类性能,且保证RCC-DTSK-C具有高可解释性.因此,本文使用0阶TSK模糊分类器作为基训练单元构造深度TSK模糊分类器RCC-DTSK-C.

2 深度0阶TSK模糊分类器

这里,我们提出一个栈式结构的深度模糊学习模型RCC-DTSK-C.该模型利用0-阶TSK模糊分类器作为一个基训练模块.

2.1 基训练单元

为了更方便解释基训练单元的实现机制,此处以单输出0阶TSK模糊分类器为例(如图1所示).

Fig.1 Base training unit corresponding to single output 0-order TSK fuzzy classifier图1 单输出0阶TSK模糊分类器对应的基训练单元

我们的工作过程分为以下几步.

(1) 直接采用P个高斯隶属函数,分别为F1,F2,…,FP,中心为[0/(P−1),1/(P−1),…,(P−1)/(P−1)].例如,如果P=3,那么隶属函数表示为F1,F2,F3,中心为[0,0.5,1],它们的语义解释为:差、中等、好.

(2) 随机生成特征选择矩阵FSM,其每一元素值通过随机分配0,1进行赋值.即FSM[fsmik]d×K:当fsmik=0时,表示第i维属性未被选中;否则,表示已被选中.其中,i=1,2,…,d,k=1,2,…,K.

(3) 随机生成规则组合矩阵RRC(random rule-combination matrix),其元素值由随机生成的0,1二值构成.RRC[3,1,4]=1表示第4条规则的第3个输入特征采用“非常差”的高斯函数,即第3维属性的F1被选中,它将被用在第4规则中.

通过以上分析,在这种0阶TSK模糊分类器中所有规则可改写为(以5维输入空间的第k条规则为例)

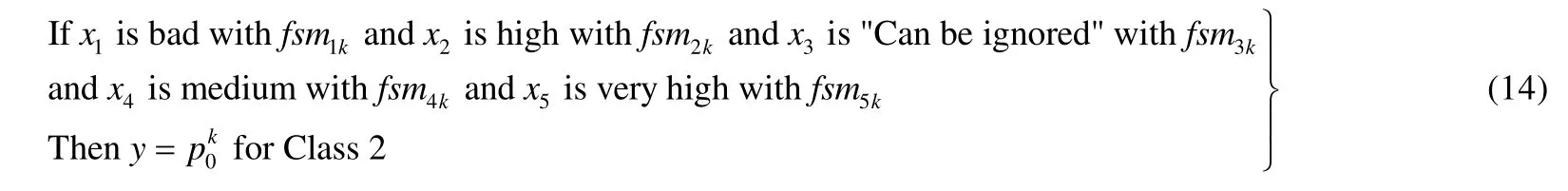
其中,“Can be ignored”表示当前这一维特征丢弃(未被选中).

2.2 栈式结构

关于本文为什么要使用栈式结构,后文有详细的解释,此处只介绍栈式结构的构成.X作为第j个基训练单元的输入,即Xj=X.当运行第j个基训练单元后,它就生成预测结果.根据栈式原理,RCC-DTSK-C将预测结果随机投影到源训练集Xj中.最终,第j+1个0阶TSK模糊分类器的输出由源训练集Xj与第j个基训练单元后的随机投影(如图2所示),即

其中,Yj是第j个基训练单元的输出;Rj是一个随机投影矩阵,其元素值由0或者1随机赋值;γ是一个很小的常数.

Fig.2 Structure of RCC-DTSK-C with single output图2 单输出的RCC-DTSK-C结构

2.3 深度TSK模糊分类器结构

近年来报道了很多关于TSK模糊模型及其应用工作[32−34],这些工作大都构造了一些不同的模糊分类器去验证分类性能和获取高的可解释性.基于栈式结构的思想,图1提出了一个基训练单位模型.该模型由单一输出的0阶TSK模糊分类器构成.图2构造了一个新的深度TSK模糊分类器.为了保证可解释性和满足Kuncheva在文献[35]中的陈述:如果隶属函数的整个选择是不一致的或者隶属函数的形状是不规则的,那么它们也不太可能与语言准确地关联.与其他报道算法不同的是,我们所提的方法通过确定隶属函数的中心很好地解释了隶属函数不规则和语言标签歧义的问题.我们随机引用了P个高斯型的隶属函数F1,F2,…,FP,比如P=3,它们的标签标记为F1:低,F2:中等,F3:高.它们分别中心化为[0,0.5,1].我们认为,规则的可解释性是设置分类器时值得考虑的一个非常重要的部分.

通常情况下,我们考虑有N对数据构成的训练集(xn,tn),其中,xn是特征向量,xn∈Rd;tn是相应输入特征向量的标签.为了方便,我们定义一个矩阵X作为训练集,T训练样本的类标签.设置X1作为原始输入的第1层,即X1=X.

我们这里提出的深度0阶TSK模糊分类器RCC-DTSK-C是深度学习的又一次尝试.该分类器构建机制类似于多层的极限学习机ELM,但是有本质的不同.在RCC-DTSK-C中,把模糊规则映射到多层TSK的每一个隐含层中.

与随机构建TSK的策略类似,RCC-DTSK-C随机分配了高斯函数的标准差、随机规则组合矩阵RRC以及特征选择矩阵FSM.RCC-DTSK-C利用由0或1二进制构成的RRC决定在某一个规则中某一个输入属性的哪个隶属函数被使用.RCC-DTSK-C提出的最大的优点是允许隶属函数不连续.比如,基于RRC,对于某个规则的输入属性,隶属函数1或者隶属函数4被选中,这就意味着RCC-DTSK-C仅仅考虑F1和F4,而隶属函数则不予考虑.然而这与文献[36]中提出的方法有区别,文献[36]方法仅限于使用连续的隶属函数.那么对于上面例子而言,文献[36]中提到的方法显然不能使用,它应该修改为:对于该条规则的输入属性而言,所有隶属函数都应该被考虑.换句话说,在F1,F2,…,FP之间的每一个隶属函数都应该被考虑.当然,这就不可避免地计算了很多无关紧要的隶属函数值,最终肯定会影响分类的精度.此外,根据后续迭代层次的数目划分了输入空间,我们使用上述设置标签的方法(F1:特别特别差,F2:特别差,…,FP:特别特别好)对输入属性进行划分,于是对每一输入属性就得到了P个划分.这里我们还设置了“Can be ignored”,利用“Can be ignored”除去部分属性,这样,模糊if-then规则就可以被重新定义.正如上面提到的每一个计算出的模糊函数值代表了一个有效的模糊输入属性,这个模糊输入属性被翻译成非常有用的规则.举例如下:

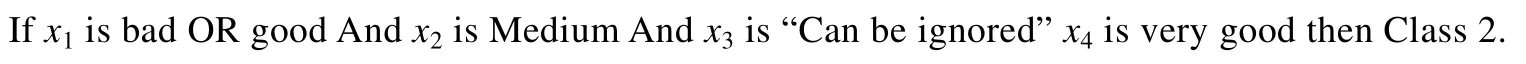
该条规则就可以重新写成:

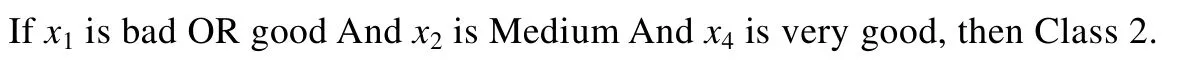
对于RCC-DTSK-C,随机输入规则数(隐含层节点数),输出y的值通过一个方程快速的计算得到.

图1展示了典型的3层TSK结构.与图1类似,图2展示了RCC-DTSK-C的基本思想.这里值得注意的是,我们所提的方法可以应用于多输入和多输出系统,具体细节将在后面章节详细讨论.

对于一个含有N个数据的训练集(含有标签)可用向量(xn,tn)表示,(xn,tn)∈Rn×Rm,其中,xn表示特征数据,tn表示标签.

2.4 RCC-DTSK-C训练算法描述

根据第2.3节的描述,本节给出RCC-DTSK-C训练算法,具体训练步骤如下.

输入和输出:

输入:训练集X=[x1,x2,…,xN]T,标签T=[t1,t2,…,tN]T,xi∈Rn,ti∈Rc;

输出:预测函数以及每个基训练单元的模糊规则.

初始化:

随机选择模糊规则数L;随机选择深度DEP;模糊划分数P;

随机生成P个高斯函数的核宽φp(φp∈R+),p=1,2,…,P

X1=X

训练过程:

fordep=1 toDEPdo

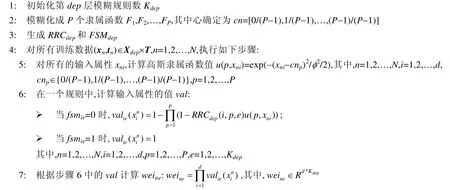
· 算法分析1

算法1中提出的规则组合矩阵RRC、特征选择矩阵FSM以及生成P个高斯函数核宽φ,它们元素的值都是随机生成,很显然,所得到的预测结果一般来讲不是很精确,但是该结果要比随机猜想的值要好一些.我们观察算法1为什么可以从定性的角度获得增强的分类性能.在步骤12中,我们可以清楚地看到,算法的每一个基训练单元都在相同的数据空间上运行,而原来的训练集落在这个数据空间中.因此,参与各基训练单元的模糊规则的每个特征都具有相同的物理解释.更重要的是,每个基训练单元运行在原来的训练集加上随机投影,即γYdepRdep.因此,即使这些附近的数据具有相同的标签,由于Rdep的随机性,相同的输出Ydep也可能会引发不同的转移到原始训练集中.我们说,对于RCC-DTSK,更好的线性可分性最终可以预测,算法1的确可以提高分类性能.

· 算法分析2

· 算法分析3

下面分析算法的时间复杂度.我们首先分析第dep个基训练单元的时间复杂度.根据算法,第dep个基训练单元的时间复杂度主要包括随机生成规则组合矩阵RRC的时间复杂度、生成特征选择矩阵FSM的时间复杂度、计算规则层输出矩阵O的时间复杂度、计算输出权重W的时间复杂度.对于RRCdep,其时间复杂度是O(PdKdep).对于FSMdep,其时间复杂度是O(dKdep).Odep的时间复杂度可由步骤6～步骤8得到,其时间复杂度是O(PNd2Kdep).很明显,步骤9中Wdep的时间复杂度是O(N3+NKdep+Nm),步骤10的时间复杂度是O(NmKdep),步骤11和步骤12的时间复杂度是O(Nd+Nmd).所以,由于m非常小,那么第dep个基训练单元的时间复杂度为

其中,d是特征数,Kdep是模糊规则数.训练模型的深度是DEP,所以整个RCC-DTSK-C时间复杂度粗略地表示为.在每个基训练单元里,模糊规则数K相对来说是比较小的,如果样本数N不是太大,那么该时间复杂度还是可以接受的.

3 实验研究

3.1 实验数据集

为了进一步表现RCC-DTSK-C的分类性能,我们采用了如表1所罗列的6个数据集[38],这些数据集可以从https://archive.ics.uci.edu/ml/datasets.html下载,其中包括小/中等/大样本数据集,大样本数据集Airline可以从http://stat-computing.org/dataexpo/2009/下载.我们还采用了0阶TSK模糊分类器、1阶TSK模糊分类器以及KEEL软件工具箱中的两个进化模糊分类器(FURIA & C4.5)在这些数据集中进行了对比.KEEL(基于进化学习的知识提取)是一种免费软件(GPLv3)Java套件,它允许用户评估不同类型的数据挖掘问题的进化学习和基于软件计算的技术的行为:回归、分类、聚类、模式挖掘等等.KEEL软件工具箱可从http:www.keel.es/download.php下载.受论文版面的限制,关于数据集更多的细节可以参考各自的网页.对于数据集Airline,1987年10月～2008年4月,航空公司的数据集包括与美国的所有商业航班的航班到达和离港详细信息.这是一个大型数据集,共有近1.2亿条记录,占用了1.6千兆字节的压缩空间和12千兆字节[39].我们挑选了1990年～1993年这4年的数据.在我们的实验中,所有数据集都被归一化.我们将每个数据集样本的75%数据用于训练,剩余部分用于测试.我们使用分类精度和训练/测试时间作为性能指标来评估所有比较分类器的性能,其中,分类精度定义为正确分类的样本数与总样本数的比率.所有实验都在具有64GB内存的E5-2609 v2 2.5GHZ CPU(2个处理器)的计算机上进行.

Table 1 Datasets表1 数据集

3.2 本文方法与其他对比方法性能比较

我们知道,虽然有很多不同的分类器被开发出来,比如BP神经网络和支持向量机,但是我们这里采用常见的0阶和1阶TSK模糊分类器[1,2]作为比较的方法,因为分类的准确性和可解释性可以同时从它们观察得到.而其他的分类器,比如支持向量机SVM和BP网络就像黑盒子.RCC-DTSK-C与其他非模糊深度分类器相比有如下优势.

a) 训练计算量小:大多数非模糊深度分类器训练通常需要很多次迭代,无疑会增加训练的计算量;而RCC-DTSK-C在训练过程中无需迭代,极大地提高了训练效率.

b) 无需大量训练样本:大多数非模糊深度分类器在很大程度上要求大量的训练样本,而RCC-DTSK-C在训练过程中只需要随机挑选部分样本数据即可.

c) 训练结果具有强的可解释性:大多数非模糊深度分类器通常输出结果难以解释,而RCC-DTSK-C的输出具有强的可解释性.

3.2.1 分类器参数设置

下面我们列出这几种分类器各自的参数设置.因为0阶TSK和1阶TSK模糊分类器都用到模糊聚类方法(fuzzy c-means,简称FCM)和SVM,所以先介绍FCM和SVM的参数设置.SVM的正则化参数设置通过网格搜索从0.01到100,步长是0.1,FCM中的聚类数和模糊规则数相等,尺度参数r值的个数可以设置网格搜索从0.01到100,步长是是0.1.对于分类器FURIA和C4.5,它们的参数则采用KEEL软件工具箱中的默认值.对于RCCDTSK-C,层数DEP的取值为2或3,数据集Balloons每一层的模糊规则数搜索范围设置为2～4,步长为1;数据集Climate-Model-Simulation-Crashes每一层的模糊规则数搜索范围设置为3～5,步长为1;数据集Airline每一层的模糊规则数搜索范围设置为150～400,步长为50;数据集Balance-Scale每一层的模糊规则数搜索范围设置为5到30,步长为1;数据集Abalone每一层的模糊规则数搜索范围设置为10～25,步长为1;数据集Yeast每一层的模糊规则数搜索范围设置为5～15,步长为1.

3.2.2 分类性能比较

由于对输入特征和模糊隶属函数都是随机选择的,那么对于一个数据集而言,RCC-DTSK-C的结构就有多种组合.对每个数据集,我们稍微改变每层规则数,并同时运行10次,取平均值,得到了平均模糊规则数、平均训练精度/平均测试精度、平均训练时间/平均测试时间.最后,我们也列出了所有数据集的平均模糊规则数、平均训练精度/平均测试精度.结果见表2、表3.

Table 2 Average number of fuzzy rules and average classification accuracies (%)表2 平均模糊规则数和平均分类精度 (%)

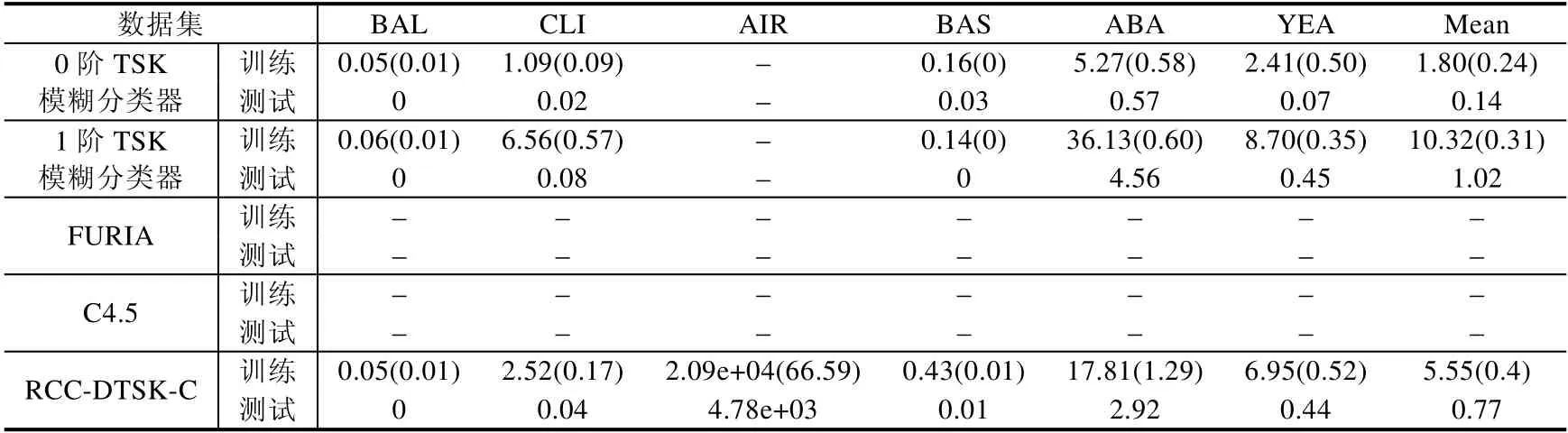
Table 3 Average training time and test time表3 平均训练时间和测试时间

根据表2,我们发现,RCC-DTSK-C几乎优于所有其他几个分类器,且取得了最好的平均分类训练精度,分别是80.63%,99.20%,91.98%和57.81%.对于AIR大样本数据集,0阶TSK、1阶TSK、FURIA和C4.5均运行相当缓慢,表2中用“---”标记;而RCC-DTSK-FC也能正常运行,这也直接说明了RCC-DTSK-C适用于大样本数据.表2中,RCC-DTSK-C的测试精度也明显高于其他分类器,这就说明RCC-DTSK-C具有良好的泛化性能.根据表3,由于FURIA和C4.5是基于JAVA平台的软件系统,时间对比没有意义,在表3中用“---”标记,这里用RCCDTSK-C与0阶TSK和1阶TSK模糊分类器进行了对比.我们发现,RCC-DTSK-C运行慢于0阶TSK模糊分类器,但是明显快于1阶TSK模糊分类器.

接下来,我们研究RCC-DTSK-C随着层数变化而引起性能的变化.表4列出了每个数据集运行10次得到的平均训练精度和平均测试精度.通过实验发现,RCC-DTSK-FC在大多数情况下可以通过多层结构达到令人满意的分类性能,层数的搜索范围为2～3.因此本文认为,RCC-DTSK-C的深度为2或3.因为在这个范围内,RCCDTSK-C的分类精度非常接近或者高于对比分类器的分类精度.根据分析,层数的选择对分类精度有影响.然而如何在每个数据集上确定RCC-DTSK-C的合适层数,是将来一个有趣的研究课题.

Table 4 Training accuracies and test accuracies of RCC-DTSK-C for different layers (%)表4 RCC-DTSK-C对于不同层的训练精度和测试精度 (%)

3.2.3 可解释性

为了更好地描述RCC-DTSK-C的可解释性,我们记录了当RCC-DTSK-C在每个数据集取得最好的精度时对应的结构.RCC-DTSK-C规则结构的表示形式为“第1层模糊规则数-第2层模糊规则数-…-第DEP层模糊规则数”.表4描述了各个数据集对应最好的精度.从表4可以看出,RCC-DTSK-C获取最好的精度时,其层数为2或3;RCC-DTSK-C获得最好的精度时,对应的结构分别为4-3-2;5-3-2;350-100-50;20-10-2;25-5-2;15-4-2.比如,4-3-2意味着RCC-DTSK-FC有3层结构:第1层、第2层和第3层的模糊规则数分别是4,3,2.

限于文章篇幅,我们这里以数据集BAL为例进一步展示RCC-DTSK-C的可解释性.由于RCC-DTSK-C的可解释性与RCC-DTSK-C的相应结构和模糊规则有关,在前面的实验中,RCC-DTSK-C在数据集BAL运行的最好精度是80.92%,其对应的结构是4-3-2.为了方便观察模糊规则的可解释性,我们取5个模糊划分数,且在RCC-DTSK-C获得的所有模糊规则中提取了前4个规则,然后在表5中对这些规则进行了总结.

Table 5 Rule presentation表5 规则展示

表5中,“Can be ignored”表示在相应的模糊规则中没有选择相应的特征.比如,我们可以方便地把表5中的规则1表示为:

其中,表5中的+1,−1分别表示数据集BAL中对应的”Inflated T”和”Inflated F”.

很明显,这种模糊规则具有很高的可解释性.

为了对RCC-DTSK-C的可解释性进行更深入的研究,表6列出了模糊划分、特征选择矩阵、规则组合矩阵、前4个模糊规则的学习参数以及每一层模糊规则“THEN-part”的输出.对于模糊划分(模糊隶属函数),不同的专家有自己的建议和理解.换句话说,对于模糊规则,其解释可能因不同的专家而异,从而只能提供模糊规则的底层解释.例如,第1个模糊规则中的模糊划分可以解释为语言意义由气球决策专家决定.因此,对于DEP=3,我们获得了相应的语言规则,见表6.

Table 6 Four rules presentation for BAL dataset表6 对于数据集BAL的4条规则展示

3.2.4 非参数统计分析

Milton Friedman[40]开发了非参数统计测试,即Friedman等级测试,用于检测多个测试中的差异.这里,我们对表1中列出的所有数据集进行Friedman排名测试.Friedman排名测试用于评估在这些数据集的多个比较方法中是否存在差异.图3显示了Friedman排名测试中这5个分类器对所有数据集的排名结果.从图3可以看出,RCC-DTSK-C在这些分类器中保持最好的排名.Friedman测试得到的相应p值为0,这表明在所有的分类器中确实存在显著的差异.总之,这些结果也表明RCC-DTSK-C明显优于其他几种分类器.

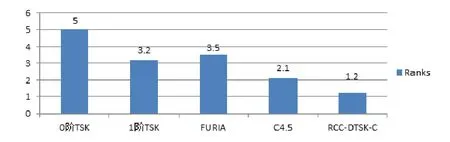
Fig.3 Nonparametric statistical analysis图3 非参数统计分析

4 结 论

本文通过栈式结构原理,以提高分类性能和较强的可解释性为目的,提出一种深度TSK模糊分类器RCCDTSK-C.RCC-DTSK-C以栈式方式构建,提出随机选取特征,不固定模糊划分和随机规则组合,生成每一个basetraining中的模糊规则.在RCC-DTSK-C的第1层和其他隐含层中始终保持相同的数据空间,使得每个隐含层的每个特征仍然保持与输入层相同的物理意义.我们对所有数据集的实证结果表明,RCC-DTSK-C在分类性能上明显优于其他几种分类器.更重要的是,通过对数据集BAL的进一步研究发现,RCC-DTSK-C还具有较强的可解释性.