格值交替树自动机∗

魏秀娟 , 李永明,2

1(陕西师范大学 数学与信息科学学院,陕西 西安 710119)

2(陕西师范大学 计算机科学学院,陕西 西安 710119)

非确定性在计算理论中有着重要意义[1−5].从逻辑层面看,非确定计算只涉及存在量词,而作为非确定的推广,“交替”在存在量词的基础上又增加了全称量词.Chandra将交替的概念与自动机相结合,提出了交替自动机的概念[6],随后,这一类型的自动机在形式化证明中被作为一种有用的模型普遍使用[7−14].

Zhou[15]在原有交替ω-有穷自动机接受条件的基础上定义了6种新形式的接受条件,并研究了交替ω-有穷自动机在这些条件下接受语言的能力.Vardi在研究线性时序逻辑[14]时,给出了用自动机理论方法来研究模型检测的新思路,即,把模型检测的可满足性问题转化为判断自动机语言是否为空的问题来讨论.Vardi运用Muller等人给出的交替(Büchi)自动机与非确定型(Büchi)自动机的等价性,为任意给定的线性时序逻辑公式构造相应的交替Büchi自动机,使得该自动机接受的语言恰好等于满足原线性时序逻辑公式的计算的全体.

Kupferman等人[16,17]定量地对交替自动机展开研究,提出了实数集上加权交替自动机的概念,并讨论了特殊语义(如Max,Sum,Sup,Lim sup语义)下加权交替(Büchi)自动机的表达能力,同时研究了特殊语义下加权交替(Büchi)自动机的代数封闭性.鉴于权值取值和语义选取的局限性,实数集上加权交替自动机的讨论较为特殊.另外,终止状态的影响并未考虑在内,这也体现了Kupferman等人[16,17]讨论的局限性.基于这些问题,Wei等人提出了格值交替自动机的概念[18],概念的创新性体现于权值的设置.文献[18]将转移的权值作为运行树叶子节点的标记,使得树语言计算简洁化,同时保证了对转移取对偶运算、终止权重取补后所得的自动机与原自动机接受语言互补这一性质;此外,Wei等人比较了格值交替自动机与格值非确定型自动机的表达能力.

树作为重要的非线性数据结构,在计算机科学中应用非常广泛.在编译源程序时,树可被用来表示源程序的语法结构;在数据库系统中,树可作为信息的重要组织形式.因此,关于输入为树结构的自动机研究也是非常有意义的.但到目前为止,针对交替树自动机的研究仅有较少学者涉及[11,19].Muller等人在文献[10,11]中针对经典情形下的交替(Büchi)(树)自动机展开讨论时指出:对交替(Büchi)(树)自动机的转移函数取对偶运算,并将终止状态和非终止状态互换所得的自动机与原自动机接受的语言互补;同时讨论了交替(Büchi)(树)自动机与非确定型(Büchi)(树)自动机的表达能力.

量化情形下输入为树(k元Σ-树)结构的交替自动机暂未有人展开讨论,针对此类计算模型是否有如上结论,本文即从此初衷展开研究且仅考虑有限输入树的情形.这里将Muller等人提出的交替树自动机的概念[10,11]和Wei等人在格值交替自动机[18]上的权值设置方式相结合,引入了格值交替树自动机的概念,讨论了其代数封闭性和表达能力.特别地,将状态转移函数取对偶运算,终止权重取补之后即可得到与原自动机接受语言互补的格值交替树自动机.此外,讨论了格值交替树自动机与格值树自动机之间的表达能力,说明了二者的等价性.最后指出可用格值非确定型自动机来模拟格值交替树自动机.

1 预备知识

首先介绍本文的预备知识,更多详细内容参见文献[18−21].

1.1 树的相关概念

定义1[20].元素组(Σ,rk)称为一个分级的字母表,其中,Σ为有限集合,rk为Σ到自然数集合N上的一个映射(在这里称为级映射).

在不引起混淆的情况下,通常用Σ表示(Σ,rk),简称字母表.对任意的k≥0,Σ(k)={σ∈Σ|rk(σ)=k}.

定义2[20].设H∩Σ=Ø.H上Σ-项(Σ-树或简称树)构成的集合TΣ(H)为满足下面两个条件的最小的集合T:

(1)Σ(0)∪H⊆T;

(2) 如果k≥1,σ∈Σ(k),且ξ1,…,ξk∈T,则σ(ξ1,…,ξk)∈T.

当H=Ø,TΣ(Ø)简记为TΣ.

定义3[20].树的高度Height和位置集Pos是从集合TΣ分别到自然数集N和由自然数集生成的幺半群的幂集P(N*)上的映射,递归定义如下.

(1) 对任意的α∈Σ(0),Pos(α)={ε},Height(α)=0;

(2) 对任意的ξ=σ(ξ1,…,ξk)∈TΣ,k≥1:

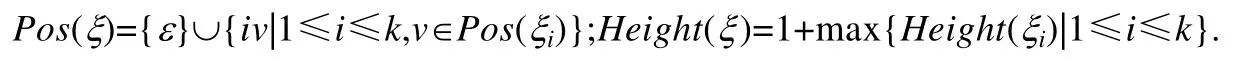
定义4[20].设ξ∈TΣ,w∈Pos(ξ),ξ(w)表示ξ在w处的标记,递归定义如下.

(1) 对任意的α∈Σ(0),α(ε)=α;

(2) 对任意的ξ=σ(ξ1,…,ξk)∈TΣ,k≥1,ξ(ε)=σ;且对于任意的1≤i≤k和v∈Pos(ξi),ξ(iv)=ξi(v).

规定位置w所在的层数称为树的第|w|层(这里的|w|表示串w的长度).

1.2 格的相关概念

定义5[21].集合X上的二元关系≤如果满足以下条件,则称≤为集合X上一个序关系,同时称X为一个偏序集.

(1) 对任意的x∈X,有x≤x成立;

(2) 对任意的x,y∈X,若x≤y和y≤x成立,则有x=y成立;

(3) 对任意的x,y,z∈X,若x≤y和y≤z成立,则有x≤z成立.

基于集合X上的序关系≤,可以定义X的子集X′的上(下)界:设x∈X,如果对任意的y∈X′都有y≤x(x≤y),则称x为X′的一个上界(下界).

X′的上确界(下确界)指的是X′的最小(大)上界(下界),用sup(X′)(inf(X′))表示.特别地,X作为自身的一个子集,若X存在上确界(下确界),则用1(0)表示sup(X)(inf(X)),并称其为X的最大(小)元.

对任意的x,y∈X,可以用∨,∧运算表示上下确界:x∨y表示sup{x,y};x∧y表示inf{x,y}.

定义6[21].设L为一个非空的偏序集,若对任意的x,y∈L,x∨y和x∧y同时存在,则称L为一个格.若格L有上下确界(同样用1,0表示),则称L为有界格.若格L中的任意元素x,y,z满足x∧(y∨z)=(x∧z)∨(y∧z),则称L为分配格.

例如,L={0,1,b1,b2,b3}(如图1所示),满足:b1∨b2=b1;b1∨b3=1;b2∨b3=b3;b1∧b2=b2;b1∧b3=b2;b2∧b3=b2.对任意的x∈L,有x∨1=1,x∧1=x,x∨0=x,x∧0=0成立.

Fig.1 Lattice L图1 格L

容易验证,L为一个有界分配格.通常情况下,用符号1⊕22来表示上述格结构.

1.3 格值树自动机

定义7[20].L上的格值树自动机是一个四元组(Q,Σ,μ,ν),其中,Q是有限状态集;Σ是一个分级的字母表;μ=(μk|k∈N)是一簇状态转移函数,;ν是格值根权向量,ν∈LQ,即ν:Q→L.格值树自动机接受的树语言(树级数)是从TΣ到格L上的映射r,对任意的ξ∈TΣ:

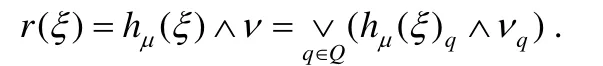
这里的hμ为从TΣ到LQ上唯一的Σ-代数,即hμ为从TΣ到LQ上的映射且满足:对任意的σ(ξ1,…,ξk)∈TΣ和q∈Q,

例如,A=(Q,Σ,μ,ν)为L=1⊕22上的一格值树自动机,其中,Q={q1,q2};Σ={σ,α},σ∈Σ(2),α∈Σ(0);非零的状态转移函数如下:

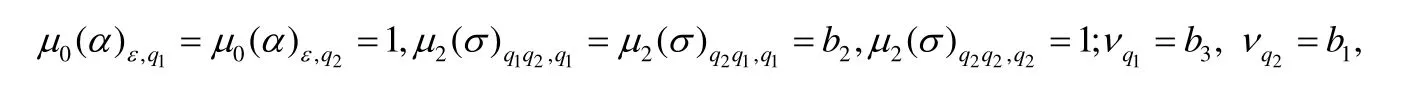
则A所对应的树语言r接受树σ(α,α)的程度如下:

1.4 交替树自动机的相关概念

对于给定的集合X,设B+(X)为X上所有正布尔公式(即X中的元素通过∨,∧运算生成的布尔公式)构成的集合,此外,要求公式true,false也在B+(X)中.

令Y⊆X,θ∈B+(X).将公式θ中属于Y的元素赋值为真,将X/Y中元素赋值为假,如果将所有元素赋值之后,最终结果为真,则称Y满足公式θ.进一步地,若Y的任意子集都不满足公式θ,则称Y以极小方式满足θ.

定义8[19].Σ上的交替树自动机是一个四元组(Q,Σ,I,Δ),其中,Q,Σ分别为有限状态集和输入字母表;I为初始状态集;Δ:Q×Σ→B+(Q×N)为状态转移函数,且对任意的q∈Q,σ∈Σ,有Δ(q,σ)∈B+(Q×{1,…,rk(σ)})成立.B+(Q×N)中的N为自然数集.

定义9[19].设ξ∈TΣ,A为Σ上的一个交替树自动机.A在ξ上的一个运行定义为一棵节点标记属于Q×N*的树t且满足:

设t(w)=(q,w′),ξ(w′)=σ并且δ(q,σ)=θ,若存在Q×{1,…,rk(σ)}的子集{(q1,i1),…,(qn,in)}满足θ,则w在t中有后继位置w1,…,wn,且这些位置的标记依次为(q1,w′i1),…,(qn,w′in).

如果运行树根节点的标记为(q,ε)且q∈I,则称该运行是可被A接受的.

1.5 格值正布尔公式

对于给定的集合X,B+(L∪X)表示X上所有格值正布尔公式(即L∪X上的正布尔公式)构成的集合.此外,要求公式true,false在B+(L∪X)中.

任给集合Y⊆X,θ∈B+(L∪X).定义格值元素v(θ,Y):将公式θ中属于Y的元素赋值为1,将X/Y中的元素赋值为0,令v(θ,Y)为θ赋值后的结果.设θ1,θ2∈B+(L∪X),若对任意的Y⊆X,都有v(θ1,Y)=v(θ2,Y)成立,则称θ1与θ2等价,记为θ1≡θ2.例如,θ1=(0.5∨(0.3∧(0.8∨x1)))∧0.2,θ2=0.2∧x1,按定义易证θ1≡θ2.

由文献[18]可知:对于任意的格值正布尔公式θ而言,均可以找到与其等价的最简终展开式,用θS表示.这里的最简终展开式意味着公式的析取范式中,析取连接词连接的任意两项不能存在包含关系,即:任意的两项,不能有l≤l′和J≤I同时成立.若为θ的最简终展开式中的一项,则称集合{xs|s∈S}以极小方式满足θ的权重为l″.对于上述θ1,θ2,可知二者有相同的最简终展开式0.2∧x1.事实上,θ1≡θ2当且仅当θ1和θ2有相同的最简终展开式.特别地,true≡1,false≡0.

2 格值交替树自动机

本节引入格值交替树自动机的概念,讨论其闭包性质以及格值交替树自动机与格值树自动机、格值非确定自动机之间的表达能力.

2.1 格值交替树自动机的概念

下文中,如果没有特别说明,L均为分配格,且包含最大元1和最小元0.

定义10.k元Σ-树上的格值交替树自动机(简称格值交替树自动机)是一个五元组A=(Q,Σ,I,δ,K),其中,Q,Σ分别为有限状态集和输入字母表,I为格值初始状态集,δ是从Q×Σ到B+(L∪(Q×K))上的映射.Q×K是所有形如(q,i)的元素构成的集合,q∈Q,i∈K,K={1,…,k}是方向集.

定义11.格值交替树自动机A在给定输入树ξ(∈TΣ)上的运行为一棵节点标记属于L∪(Q×K*)的树t,且满足:

(1) 如果t(ε)=(q,ε),则I(q)≠0.

(2) 设t(w)=(q,w′),ξ(w′)=σ(σ∈Σ(k))且δ(q,σ)=θ(θ≠true).若存在Q×{1,…,rk(σ)}的某个子集{(q1,i1),…,(qs−1,is−1)}以极小方式满足θ的权重为l(l≠1),则w在t中的后继位置有w1,…,ws,且这些位置的标记分别为l,(q1,w′i1),…,(qs−1,w′is−1).若存在集合{(q1,i1),…,(qs−1,is−1)}以极小方式满足θ的权重为1,则w在t中有后继位置w1,…,w(s−1),且这些位置的标记分别为(q1,w′i1),…,(qs−1,w′is−1)(后一种情形下相当于l=1,从下文格值交替树自动机接受语言的定义可以看出,此处的1并不影响接受语言的程度,为了计算方便略去不标).

(3) 如果t(w)=(q,w′),ξ(w′)=σ(σ∈Σ(k))且δ(q,σ)=true,则w在t中只有1个后继位置w1,节点标记为1(此处的1不省略是为了使所有叶子节点都有格值标记).

(4) 如果t(w)=l,则w没有后继位置.

设A为格值交替树自动机,A所接受的语言rA为从TΣ到格L上的映射,定义如下:对任意的ξ∈TΣ,

其中,RA(ξ)表示A在给定输入树ξ上的所有运行树构成的集合,(q,ε)为运行树t的根节点的标记.wt(t)表示运行树t的权重,该值等于t的所有叶子节点标记的合取值.根据运行树的定义可知,t的所有叶子节点的标记均为格值元素,即wt(t)等于t中出现的所有格值元素的合取值.

若运行t使得t(ε)=(q,ε)且I(q)∧wt(t)≠0成立,则称t为可被A接受的运行.

例1:令L=1⊕22(如图1所示).设A=(Q,Σ,I,δ,K),其中,Q={q0,q1,q2},Σ={σ,α},K={1,2}.其中,σ∈Σ(2),α∈Σ(0),初始权重为:I(q0)=b1,I(q1)=I(q2)=0.状态转移函数为:δ(q0,σ)=(b1∧(q1,1)∧(q1,2))∨(b2∧(q2,1))∨b3;δ(q0,α)=true;δ(q1,σ)=b2∧(q2,1);δ(q1,α)=true;δ(q2,σ)=b1∧(q1,2);δ(q2,α)=false.

给定输入树ξ=σ(σ(α,α),α),由定义11可知ξ上的接受运行树有两棵,记为t1,t2,如图2所示.

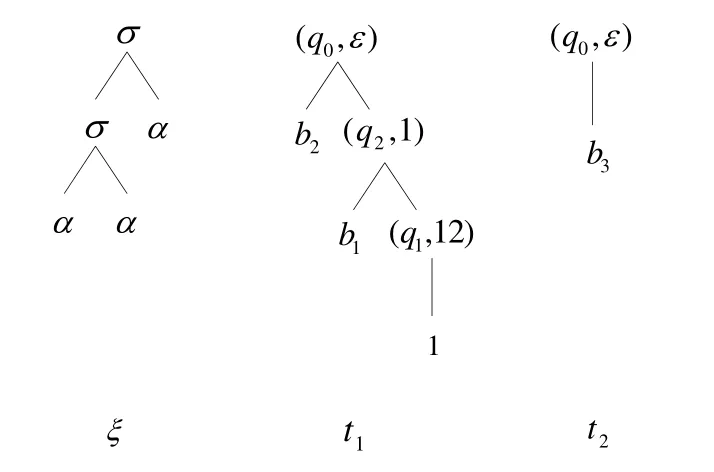
Fig.2 All accepting runs of A on ξ图2 A 在ξ上的接受运行树

格值交替树自动机A接受ξ的程度为

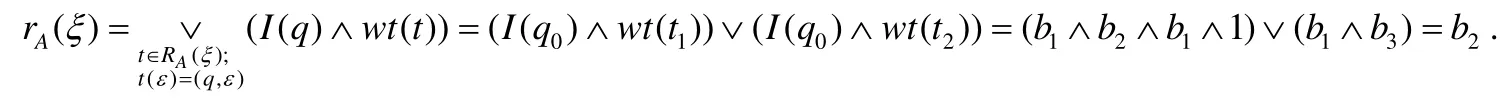
为了下文叙述方便,将t中非叶子节点的标记(状态和位置构成的二元对)中的第1分量称为状态指标,第2分量称为位置指标.

2.2 格值交替树自动机的闭包性质

从代数角度研究各种不同类型的自动机[22−25],讨论其是否构成一个封闭的代数系统是对自动机本身性质的探讨,也是保证其运算合理性的前提.这一节针对本文提出的格值交替树自动机的封闭性问题进行研究.

对于经典的交替树自动机而言,文献[10]借助计算树的概念和Game-理论证明了对交替树自动机的转移函数取对偶运算,将终态和非终态互换即可得到与原交替自动机互补的另一交替自动机.本节旨在文献[10]的基础上研究格值交替树自动机的补运算,并证明其封闭性.由于要考虑补运算,所以这一节中用到的格含有补运算记作c,即c是格L上的一元运算且满足:对任意的l,l1,l2∈L,有l=c(c(l))和l1≤l2⇔c(l2)≤c(l1)成立[21].

引理1.对于任意的格值交替树自动机,均存在与其等价的且具有唯一初始状态的格值交替树自动机.

证明:设A为格值交替树自动机(Q,Σ,I,δ,K)构造A′=(Q∪{q0},Σ,q0,δ′,K):A′在A的状态集基础上添加一个额外状态q0,作为A′的唯一初始状态;对任意的σ∈Σ,添加转移函数;对任意的q∈Q,σ∈Σ,令δ′(q,σ)=δ(q,σ).

由A′的构造可知,初始自动机A与目标自动机A′在任意给定的输入树上的运行树一一对应:事实上,A在任意的输入树ξ上的运行树t,其中,t(ε)=q′且I(q′)≠0,对应于A′在ξ上的运行树t′,其中,t′(ε)=q0且wt(t′)=I(q0)∧wt(t),因此A与A′等价:

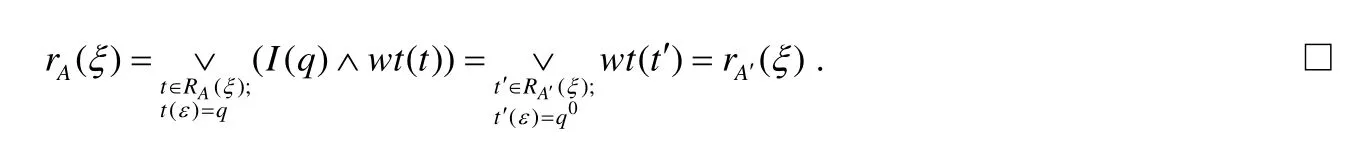
有引理1的保证,在接下来的讨论中如果没有特殊说明,则仅考虑具有唯一初始状态的格值交替树自动机.

定理1.k元Σ-树上的格值交替树自动机关于交、并运算封闭.

定义k元Σ-树上的格值交替树自动机:

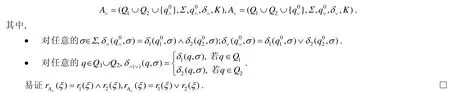
定理2.k元Σ-树上的格值交替树自动机关于补运算封闭.

为了证明定理2,需要借鉴参考文献[10]的记号和定义而引入一些新的概念.在介绍新概念之前,首先介绍Q×K上的格值正布尔公式(L∪(Q×K)上的正布尔公式)的对偶运算.

对于Q×K上的格值正布尔公式,定义对偶运算:

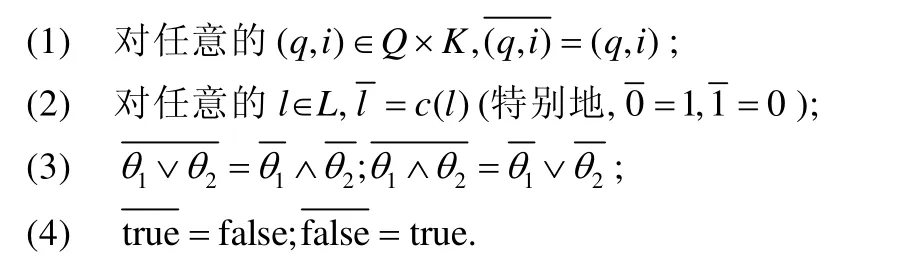
对格值交替树自动机A的所有转移函数取对偶运算、终止权重用其补元代替,即可得到一个新的格值交替树自动机,用表示.定理2可等价表述为是一个与A互补的k元Σ-树上的格值交替树自动机.

定义12.格值的n步ID(n≥0),记作FHn,为所有形如h1,h2的元素构成的集合,其中,

·h1=(q0,ε)k1(q1,k1)k2(q2,k1k2)…kn(qn,k1…kn);

·h2=(q0,ε)k1(q1,k1)k2(q2,k1k2)…kt(qt,k1…kt)k′(l),t≤n−1,ki∈K(i=1,…,n),k′=0.

这里的0表示自然数0,并非格中的零元),l∈L.

注意到,FHn∩FHn+1≠Ø.

定义13.对于FHn中的任意元h以及L∪(Q×K)中的任意元g,定义h,g的连接.

下面引入格值计算树的概念.

定义14.设A为一格值交替树自动机,ξ为给定的输入树,递归定义A在ξ上的格值计算树T(A,ξ)如下.

例2:设A=(Q,Σ,q0,δ,K)为一个具有唯一初始状态的格值交替树自动机,Q,Σ,δ,K的定义与例1一致.求A在输入树ξ上的格值计算树.根据定义14可得T(A,ξ),如图3所示.

Fig.3 Computation tree of A on ξ图3 A 在给定的输入树ξ上的格值计算树

除了按照定义11求格值交替树自动机接受的语言rA(ξ)外,可以根据A在ξ上的格值计算树T(A,ξ)的最后一层节点的标记得到rA(ξ),只需将T(A,ξ)每条分支上标记结尾处的格值合取,然后再将不同分支上所得结果取析取运算.对例2用这种方法,有结果(b2∧b1∧1)∨b3=b3.

设T(A,ξ)是A在ξ上的格值计算树.取任意的i(0≤i≤Height(t)+1),且h′,…,h(k)分别为T(A,ξ)第i层的k个节点的标记,则称h′∨…∨h(k)为T(A,ξ)第i层的总表达式.借助该定义可将求证定理2转化为求证T(A,ξ)第Height(ξ)+1层的总表达式与第Height(ξ)+1层的总表达式互为对偶关系.

现在来证明该结论.

证明:设hi为T(A,ξ)第i层的总表达式,0≤i≤Height(ξ)+1.由定义14可得到hi与hi+1有关系δi(hi)=hi+1.

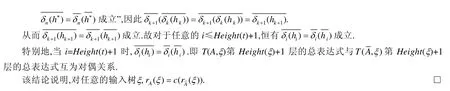
2.3 格值交替树自动机的表达能力

这一节主要讨论格值交替树自动机、格值树自动机以及格值非确定自动机之间的表达能力.首先证明格值交替树自动机和格值树自动机有相同的表达能力.

定理3.对于任意的格值树自动机,存在与其等价的格值交替树自动机.

下面给定理3对应的算法表示.

算法1.

输入:格值树自动机A=(Q,Σ,q0,μ);

输出:格值交替树自动机A′=(Q,Σ,q0,δ,K).

算法1的时间复杂度完全取决于δ的构造,而δ的构造同时取决于q,σ以及q1,…,qk的选取,则该算法的时间复杂度为O(|Q|×|Σ|×|Q|m),即O(|Q|m+1×|Σ|),其中m=max{rk(σ)|σ∈Σ}.

下面说明算法1输出的自动机即为与输入的格值树自动机等价的格值交替树自动机.

对任意的输入树ξ,只需证明A在ξ上的接受运行与A′在ξ上的接受运行一一对应,且二者权重相等.

事实上,将A在ξ上的任意接受运行的叶子(格值标记)节点和非叶子节点标记的第2指标去掉(只留状态指标)后,即得到A′在ξ上的一个接受运行,且二者权重相等.反之,将A′在ξ上的任意接受运行的每个非叶子节点标记换成元素对,令元素对的第1指标等于该位置的原始标记,第2指标等于该节点的位置,并将每步转移的权重标出.即将转移标在(q,w)的下一行的最左端,作为叶子节点标记,与同行的节点标记从左至右依次为(q1,w1),…,(qk,wk).经过上述转化,即得到A在ξ上的一个接受运行,且与A′在ξ上的接受运行权值相同.

例 3:设A=(Q,Σ,q1,μ)为格值树自动机,其中,L=1⊕22,Q={q1,q2},Σ={σ,α},σ∈Σ(2),α∈Σ(0);.下面构造与A等价的格值交替树自动机A′.

令A′=(Q,Σ,q1,δ,K),其中,K={1,2};δ(q1,σ)=(b1∧(q1,1)∧(q2,2))∨(b1∧(q2,1)∧(q1,2));δ(q2,σ)=b3∧(q2,1)∧(q2,2);δ(q1,α)=b2;δ(q2,α)=1.

取ξ=σ(σ(α,α),α),A在ξ上的接受运行记为t1,t2,t3,相应地,A′在ξ上的接受运行为(如图4所示).

Fig.4 All accepting runs of A,A′ on the input tree ξ图4 A,A′在给定的输入树ξ上的所有接受运行

定理4.对于任意的格值交替树自动机,存在与其等价的格值树自动机.

由于定理4的证明并不直观,故在给出其算法和形式化证明之前先用例子来说明构造思路.

同样地,这里仅考虑具有唯一初始状态的格值交替树自动机C=(Q,Σ,q2,δ,K).其中,L=[0,1];Q={q1,q2,q3,q4,q5},Σ={σ,α,β},σ∈Σ(2),α,β∈Σ(0),K={1,2}.状态转移函数见表1.

Table 1 Transition functions表1 状态转移表

对于给定的输入树ξ,将C在ξ上的任意接受运行t按下列方法转化为t′的形式.

(1) 令t′(ε)等于t(ε)二元组中的状态指标q2.

(2) 将第1层所有非格值元素按第2个指标分类,指标一致的放在一起,且将不同组的元素按第2指标的字典序从左到右排列.将排列好的每组中元素位置指标省去,形成新的多元状态组P1,…,Prk(ξ(ε)),并将这些多元状态组作为t′(ε)的后继状态.令等于第1层出现的格值元素;若没有格值元素出现则令其为1,其中,Pi为新形成的第i个状态组(i=1,…,rk(ξ(ε))).即将q2,q4放在一起为一个二元状态组,记为(q2,q4);q1单独为一组.令(q2,q4)和q1为t′(ε)的后继状态,且

(3) 将t第1层中同属于第i个状态组的元素全部拿来,把它们的非格值后继按步骤(2)中的方法分类合并排列,略去第2指标,并将这些新的多元状态组作为t′(i)的后继.令转移权重等于第i个状态组的所有格值后继的合取值;若没有格值后继,令权重为1.即(q2,q4)的后继从左至右为(q1,q3,q4)和(q2,q3),且等于其格值后继.

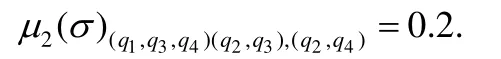
(4) 对每层元素重复过程(3),直到t的第Height(t)层元素全部按照步骤(3)转化后立即停止(结果如图5、图6所示).

若某个状态组仅有格值后继,例如节点标记(q1,2),则令

将C在ξ上的接受运行t转化为t′的过程中所构造的状态转移函数有:

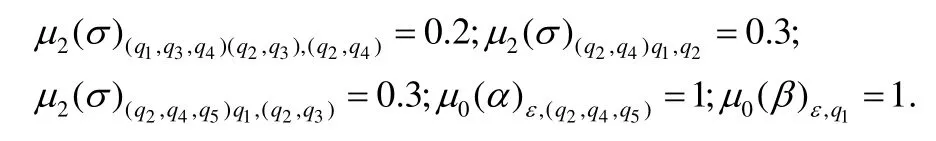
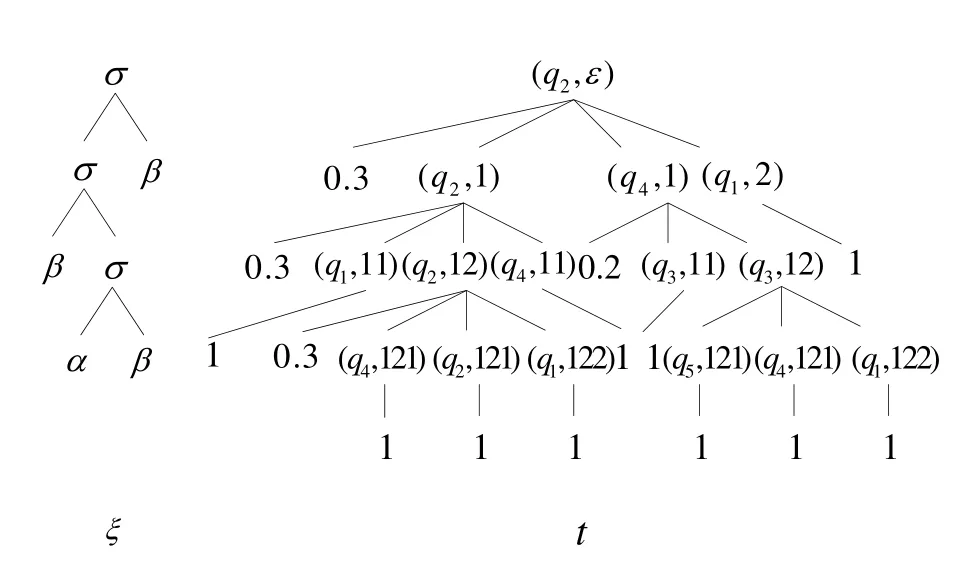
Fig.5 An accepting run of C on input tree ξ,denoted by t图5 C在给定的输入树ξ上的某一接受运行t

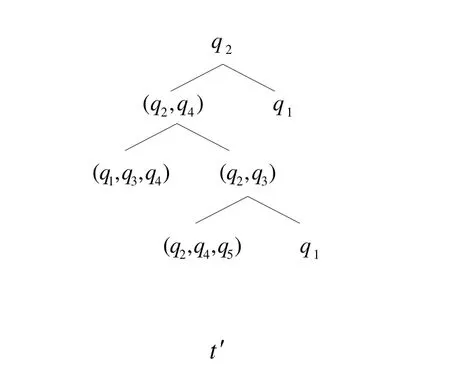
Fig.6 A run corresponding to t图6 将t 按上述方法转化而得的t′

注意到,第(2)步形成的新的元素组个数不大于rk(ξ(ε)).若个数小于rk(ξ(ε)),则需引入额外状态,使得加入额外状态之后总的后继个数等于rk(ξ(ε)).同理,第(3)步、第(4)步两个步骤中也可能遇到这样的情况,也要做相同的处理,具体做法见算法2.算法中提到的q*即为引入的额外状态.算法2为定理4所对应的将给定的格值交替树自动机转化为与之等价的格值树自动机的算法表示.

注:下文中出现的δS(q,σ)为δ(q,σ)的最简终展开式,相同的表示不再赘述.

算法2.

输入:格值交替树自动机A=(Q,Σ,q0,δ,K);

输出:格值树自动机A′=(Q′,Σ,q0,μ).

算法的时间复杂度完全取决于μ的构造,而μ的构造同时取决于状态、字母表元素和项u1,…,un的选取.在构造Ai的过程中要进行|K|⋅|Q|次比对,故该算法的时间复杂度为O((|K||Q|+1)|Q|×|Q|×|Σ|×|K|).

文献[19]中交替树自动机到树自动机的转换,构造的树自动机的状态集为初始输入的交替树自动机状态集的幂集,转移函数为f(S1,…,Sn)→{q∈Q|S1×{1}∪…∪Sn×{n}满足Δ(q,f)}.构造过程要考虑任意的n(1≤n≤max{rk(f)|f∈Σ})元状态组的转移.这里,状态组中的每个分量Si为初始输入的交替树自动机状态集的幂集的子集.上述算法2的构造,格值树自动机的状态集是以初始格值交替树自动机的状态为基础的n(1≤n≤|Q|)元元素组构成的集合,且构造转移函数过程中需要考虑每个这样的元素组.

由算法2可得:对于A的任意一棵运行树t,对应地可找到A′的若干棵运行树t1,…,tp,使得wt(t1)∨…∨wt(tp)=wt(t);反过亦有类似结论.

事实上,对于A′的任意运行树t′,与t′等价的A的运行树t满足:

(1)t(ε)=(t′(ε),ε).

(2) 设t′的第1层的标记从左至右依次为P1,…,Ps,若P1,…,Ps中没有等于q*的,则(q,i)为t(ε)的后继节点的标记,其中,q∈Pi(i=1,…,s),为t的第1层中唯一的格值标记,且放置在第1层的最左端;若P1,…,Ps中存在Pj等于q*,则(q,i)为t(ε)的后继节点的标记,其中,q∈Pi(对于任意的i≠j),同样地,为t的第1层中唯一的格值标记,且放置在第1层最左端.

(3) 对于t的第1层中任意的(q,i),找到δS(q,σ)中项,使得任意的处在t′的第ii″个位置的多元状态集中,则为(q,i)的一个后继节点标记,lj为(q,i)的后继节点中唯一的格值标记,且放置在(q,i)所有后继节点的最左端.依次考虑其他状态,直到全部状态均满足上述条件完毕,得到t.

例4:设L=[0,1],A=(Q,Σ,I,q0,K)是一格值交替树自动机,其中,Q={q0,q1},Σ={σ,α},σ∈Σ(2),α∈Σ(0K={1,2},状态转移函数为δ(q0,σ)=(0.2∧(q0,1)∧(q1,1)∧(q1,2))∨(0.3∧(q0,2));δ(q0,α)=true;δ(q1,σ)=0.5∧(q0,2);δ(q1,α)=false.

按定理4方法构造与A等价的格值树自动机A′如下.

A′=(Q′,Σ,q0,μ),其中,Q′=Q∪Q2∪{q*};转移函数定义如下:

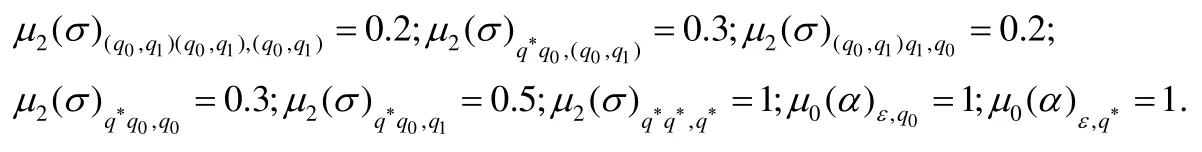
其他没有提到的转移权重为0.

以输入树ξ=σ(σ(α,α),σ(α,α))为例说明A在ξ上的运行与A′在ξ上运行的对应关系,如图7、图8所示.

Fig.7 All accepting runs of A on input tree ξ,denoted by t1,t2图7 A 在给定的输入树ξ上的所有接受运行t1,t2

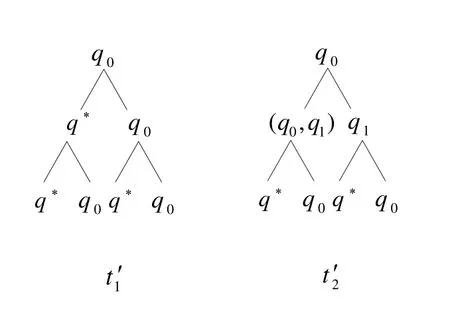
Fig.8 All accepting runs of A′ on input tree ξ,t1,t2 denoted by 图8 A′在给定的输入树ξ上的所有接受运行

A接受ξ与A′接受ξ的程度分别为:

其中,ξ1=ξ2=σ(α,α).

接下来讨论如何利用格值非确定自动机来模拟格值交替树自动机.这里的模拟是指:对于格值交替树自动机的任意输入树,存在格值非确定自动机中的输入字符串使得前者的接受程度等于后者;同样地,对于格值非确定自动机的任意输入字符串,存在格值交替树自动机的输入树,使得二者被接受的程度相等.这里的模拟包含着“等价”的含义,但并非实质上的等价,因为前者接受的是树,后者接受的是字符串.

定理5.设A是一格值交替树自动机,则可找到格值非确定自动机来模拟A.

类似地,在给出定理5的形式化证明前,先通过一个例子来说明构造思想.

这里仍然采用定理4证明前的例子.将ξ上的运行t转化成串w上的路径P,方法如下.

(1) 将ξ=σ(σ(β,σ(α,β)),β)每层字符按照其位置的字典序排列,并将其位置标于该字符右下角处.将每层所得到的字符串依次连接,得到新的字符串w=σε(σ1β2)(β11σ12)(α121β122).每个字符组可看作单个字符属于的情况,例如

(2) 将{(q2,ε)}作为路径P的初始状态;把t的第1层的非格值元素放在一起作为一个整体,将其作为{(q2,ε)}经过字符σε输入后可能到达的后继状态,并令转移权重为该层出现的所有格值元素的合取值.{(q2,ε)}经过σε输入,可能到达状态{(q2,1),(q4,1),(q1,2)},且转移权重δn({(q2,ε)},σε,{(q2,1),(q4,1),(q1,2)})=0.3.对每层元素重复过程(2),直到t的第Height(t)+1层停止.

将t按上述方法转化得到路径P(P可看作某一格值非确定自动机的运行路径):

另外,在定理5证明之前需引入完备的格值交替自动机的概念,该概念在证明中有重要作用.

定义15.若格值交替树自动机满足:对任意的q∈Q,σ∈Σ,当δ(q,σ)≠true且δ(q,σ)≠false时,对于δS(q,σ)中的任意一项,任取0≤k≤rk(σ),均存在第2指标为k的元素对出现在该项中,则称该格值交替树自动机是完备的.

注意到,例1中提到的格值交替树自动机不是完备的,比如对于δS(q0,σ)的第2项b2∧(q2,1),该项缺少第2指标为2的元素对;对于第3项b3,该项既缺少第2指标为1又缺少指标为2的元素对.

可以证明,格值交替树自动机和完备的格值交替树自动机有如下关系.

命题5.对于任意的格值交替树自动机,存在与其等价的完备的格值交替树自动机.

证明:设A=(Q,Σ,q0,δ,K)为任意的格值交替树自动机.构造A′=(Q∪{qΔ},Σ,q0,δ′,K):

(1) 将破坏A完备性的转移全部取出,做如下处理:若δS(q′,σ)中存在某项使得u中不存在第2指标为j(j∈{1,…,rk(σ)})的元素对,则将(qΔ,j)添加到u中.重复上述过程,直到最后得到的u′中存在第2指标为j′(j′=1,…,rk(σ))的元素对时结束.将δS(q′,σ)中每一项进行改造得到δ′(q′,σ);

(2) 增加转移:对任意的σ∈Σ,令δ′(qΔ,σ)=true.

从构造中不难看出,步骤(1)、步骤(2)两步之后使得某些运行树仅增加了一些叶子节点为1的分支,故不改变整体权重,从而A和A′等价.□

例5:将例2中的格值交替树自动机转化为与其等价的完备的格值交替树自动机.

δS(q0,σ)中第2项b2∧(q2,1)缺少第2指标为2的元素对,将第2项中添加(qΔ,2),使其变为b2∧(q2,1)∧(qΔ,2);同理,第3项0.2既缺少第2指标为1又缺少指标为2的元素对,则添加(qΔ,1)和(qΔ,2),使其变为b3∧(qΔ,1)∧(qΔ,2).令添加过后的公式等于δ′(q0,σ).

按照上述做法得到的另一格值树自动机A′=(Q∪{qΔ},Σ,q0,δ′,K)的转移函数如下.

·δ′(q0,σ)=(b1∧(q1,1)∧(q1,2))∨(b2∧(q2,1)∧(qΔ,2))∨(b3∧(qΔ,1)∧(qΔ,2));

·δ′(q0,α)=true;δ′(q1,σ)=b2∧(q2,1)∧(qΔ,2);

·δ′(q1,α)=true;δ′(q2,σ)=b1∧(qΔ,1)∧(q1,2);

·δ′(q2,α)=true;δ′(q*,σ)=true;δ′(q*,α)=true.

ξ上的接受运行如图9所示.

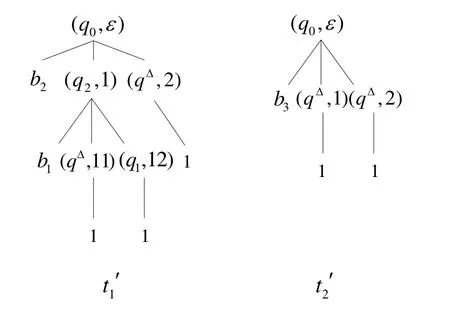
Fig.9 All accepting runs of A′ on input tree ξ,denoted by 图9 A′在给定的输入树ξ上的所有接受运行

下面来证明定理5,这里只需考虑完备的格值交替树自动机即可.

An的状态个数跟K*的基数有关,所以定理5构造的格值非确定自动机的“有用”状态可能无限.由于定理5的研究是为了在理论上揭示交替树自动机和非确定自动机的内部联系,故即使出现无限状态,也并不会到影响二者的联系和转化过程.

例6:令L=1⊕22.设A=(Q,Σ,q1,δ,K),其中,K={1,2};δ(q1,σ)=(b2∧(q2,1)∧(q3,2))∧(b3∧(q3,1)∧(q2,2));δ(q2,σ)=b1∧(q3,1)∧(q3,2);δ(q3,σ)=false;δ(q1,α)=false;δ(q2,α)=true;δ(q3,α)=true.

A的所有接受运行树有4棵,记为t1,t2,t3,t4,它们分别是在输入树ξ1,ξ1,ξ2,ξ3上的接受运行(如图10所示).

Fig.10 All accepting runs of A,denoted by t1,t2,t3,t4图10 A 的所有接受运行t1,t2,t3,t4

综上所述,A在W1中任意串上的路径p1∈P1(p2∈P2)模拟A′在ξ1上的运行t1(t2),A在W2中任意串上的路径p3∈P3模拟A′在ξ2上的运行t3,A在W3中任意串上的路径p4∈P4模拟A′在ξ3上的运行t4.

3 总结

本文引入格值交替树自动机的概念并对其闭包性质和表达能力展开研究.证明了格值交替树自动机关于交、并、补运算封闭,特别地,利用格值计算树的概念证明了只需对状态转移函数取对偶运算、将终止权重取补即可得到与原格值交替树自动机互补的另一格值交替树自动机.此外,证明了格值交替树自动机与格值树自动机的等价性.这为格值树自动机的补问题提供了另一思路.进一步地,本文指出,可以利用格值非确定型自动机来模拟格值交替树自动机.这一结论体现了非确定型自动机和交替树自动机这两类不同模型之间的内在联系.如何将这些结论推广到无限树上,且如何利用这些自动机理论的结果去讨论计算树逻辑模型检测问题,有待于进一步探讨.