一种量词约束满足问题的混合易解子类∗
2019-10-26高健,陈荣,李辉
高 健, 陈 荣, 李 辉
(大连海事大学 信息科学技术学院,辽宁 大连 116026)
约束是一个现实世界普遍存在的概念,它在工业领域和日常生活中都有体现,如生产过程中加工产品的先后顺序、字处理软件排版对齐的方式、棋类游戏中的限制规则等,都是常见的约束关系.约束满足问题(constraint satisfaction problem)[1]是人工智能领域中核心的研究方向之一,它用来刻画客观存在的约束关系,并被广泛地应用于建模和求解各类实际问题[2−4],如作业调度、智能规划、产品配置等.量词约束满足问题(quantified constraint satisfaction problem)[5]是经典约束满足问题的重要扩展,在该问题中引入了一个变量顺序的前缀,每个变量还被一个量词所限定,量词的种类有全称量词和存在量词.求解量词约束满足问题是十分复杂的,对于由全称量词限定的变量,求解过程需要为其每个可能的取值找到一组其后续变量的赋值,并满足它们之间的约束关系.从计算复杂性的角度来讲,量词约束满足问题是PSPACE-完全的.而作为该问题的子问题,量词布尔范式(quantified Boolean formula)[6]是PSPACE-完全类中的原型问题,即最早被证明是PSPACE-完全的,因此,量词约束满足问题的求解难度通常难于传统的约束满足问题.近些年,量词约束满足问题在博弈论、机械产品设计、动态调度等领域被广泛应用[7−10].例如,在博弈游戏中,人们往往需要找到一个策略,使得无论对方如何选取决策都能保证是可以获胜的;在工业产品配置中,为了提高产品的竞争力,生产商需要寻求一种满足客户各种可能需求的配置方案.量词约束优化问题也得到关注,Lallouet等人[11,12]提出了Minimax加权约束满足问题,该问题模型用于存在竞争对手的交互式决策问题中,目标是在竞争对手采取对自己最不利的决策时,最优化给定的目标函数.
由于量词约束满足问题可以用于描述诸多实际问题,因此对该问题的性质分析受到了学者的重视,而其中,对约束特性的分析是设计约束求解算法的基础[13,14].虽然目前求解算法主要采用基于回溯策略的系统搜索方法,如Gent等人提出的QCSP-Solve[2,15]求解算法,但是算法中通常需要启发式和局部结构化简技术,如基于相容性技术的变量值域约减和预处理方法.另外,利用问题的结构特征设计启发式规则也是一种重要的方法.例如,利用子问题结构的相似性搜索结果的复用技术在求解器中也经常被使用.Bacchus等人[16]提出了基于解重用的回跳技术,该技术在搜索算法找到满足约束的一个分支后,判断当前存在量词变量的赋值是否同时也是其他分支(即其他的全称量词变量赋值组合)的解,与当前赋值相容的其他分支则被标记,在后续的搜索中不再展开这些被标记的分支,从而减少了重复的计算;而求解算法Block-Solve[17]先将问题分解,求解若干子问题后,将计算结果整合成整体问题的解.另一方面,隐蔽集(backdoor set)[18]是分析问题结构特征的一项重要理论工具.它是一个变量的集合,当该集合中所有变量被赋予某一组取值后,剩余的子问题可以很容易地(通常在多项式时间内)被求解.隐蔽集理论可以用来识别问题中隐含的易解结构,通过它,可以找出哪些问题是多项式时间内可解的,或者识别出多项式时间内可解的部分,并从问题中将容易求解的部分分离出来.该项理论在分析约束满足问题和量词约束满足问题中都起到了重要的作用[19−21].然而在寻找一个隐蔽集的同时,需要确定剩余的变量组成的子问题是否是多项式时间可解的,所以隐蔽集的研究又是以多项式时间易解子类(以下简称易解子类)为基础的[22].
约束满足问题的易解子类[23]是指该问题集合中的特例子集,这个子集中的问题实例可以在多项式时间内求解.寻找易解子类是约束满足问题的一项重要的基础研究.而量词约束满足问题是PSPACE-完全的,所以找出该问题的可解子类,可以更大幅度地化简问题结构并提高求解效率.因此,易解子类的研究也在量词约束满足问题中展开,并为隐蔽集的分析提供了理论基础.寻找更一般化的易解子类是获得更小隐蔽集的关键所在,本文研究量词约束满足问题的易解子类,首先提出了针对全称量词变量的相容性概念并分析了其相关算法的时间复杂度.基于此概念,提出了一种新的混合易解子类,该易解子类一般化了基于Broken-Tringle Property(BTP)的易解子类[24].本文还详细分析了所提出的混合易解子类的相关性质,其中包括子类识别问题所需的时间复杂度,并证明部分变量赋值后的子问题保持了量词相容性和易解属性.本文还在约束满足问题的隐蔽集定义基础上定义了量词约束满足问题的隐蔽集,通过改造经典的回溯求解算法,实验分析了所提出的易解子类对隐蔽集大小的影响.通过与原有基于BTP的易解子类的实验结果比较,可以看出该易解子类可以获得更小的隐蔽集,从而有效地将更多的变量分离到易解部分.
1 量词约束满足问题的定义
约束满足问题包括有限变量集合和有限约束集合,每个变量对应一个有限论域,每条约束限制了一些变量允许赋值的组合.约束满足问题的解是为每个变量赋一个对应论域上的值,使之满足所有约束.求解约束满足问题的目标是找到一个解或是全部解.事实上,量词约束满足问题是通过经典约束满足问题对每一个变量都限定一个存在(∃)或者全称(∀)量词扩展而来的.同时,量词约束满足问题也是量词布尔范式的扩展,量词布尔范式中,每个变量都在布尔域上取值,即取“真”或者“假”,而量词约束满足问题的变量值域可以是任意的有限集合.因为量词布尔范式是PSPACE-完全类中的原型问题,所以量词约束满足问题也是PSPACE-完全的.
量词约束满足问题可以定义成一个四元组的形式(X,D,C,Q)[2],其中,
·X是一个有序的变量集合{x1,x2,…,xn};
·D={D1,D2,…,Dn}代表了对应变量的取值范围,函数D(xi)表示变量xi的值域(1≤i≤n);
·C={c1,c2,…,ce}是一个约束集合,每个约束限制了若干变量允许取值的关系元组;
·Q={λ1x1,λ2x2,…,λnxn}是一个有序的量词集合,λi∈{∃,∀}(1≤i≤n).
函数Var(ci)(1≤i≤e)定义为参与约束ci的变量集合.
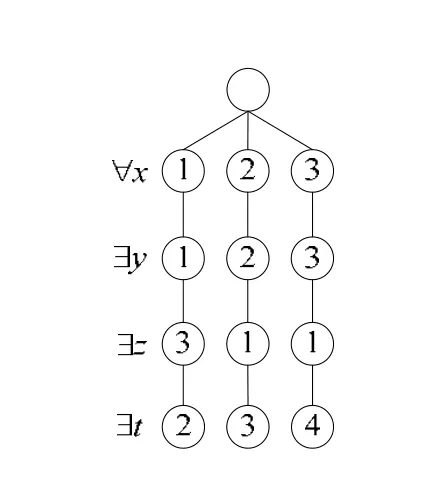
量词约束满足问题P=(X,Q,D,C)表示逻辑公式λ1x1λ2x2…λnxn(C),所以变量在P中是有序排列的,变量xi在xj之前是指xi在前缀中出现在xj之前,记作xi≺xj或i 给定一个量词约束满足问题,如果对于所有的约束ci(1≤i≤e)都有|Var(ci)|=2,则该问题是二元的;如果存在约束ci使得|Var(ci)|>2,则说该问题是非二元的.本文主要探讨二元量词约束满足问题,因此,cij被用来表示变量xi与xj之间的约束.这里包含了平凡约束,即在此约束里,所有的关系元组都是允许的.函数R(xi,xj)表示约束cij中允许取值的二元组集合.X∀表示全部全称量词变量集合,X∃表示全部存在量词变量集合.z为变量,X∀(z)表示在z之前的全称量词变量集合. 值a被赋给变量y时,称a为y的赋值,记作y=a;一组赋值α=a1a2...ak被赋给变量集合Y⊆X时,称α为Y的一组赋值,记作Y=α.若α和β分别是一组赋值且α和β所包含的变量交集为空,则αβ表示两组赋值的并集.在本文中,a,b和c通常用于表示单个变量的赋值,而α和β表示对一组变量的赋值.若y=a是一个赋值且z是变量,则z中与a相容的所有值组成了a关于z的支持集,记作Iz(a);若α是Y的一组赋值,则变量z中所有与α相容的值的集合记作Iz(α).支持集集合Πy(∀)={Iy(α),其中,α为任意一组X∀(y)的赋值}.若β为一组对存在量词变量的赋值,Πy(∀,β)={Iy(αβ)|其中,α为任意一组X∀(z)的赋值}. 若α为一组赋值,则P(α)表示通过α赋值对P化简后的问题,即从P中删除被赋值的变量和这些变量参与的约束,同时删除未赋值变量中与α不相容的取值并在未赋值变量的约束中删除不相容的取值参与的元组关系后,得到的P的化简问题. 例1:二元量词约束满足问题P的约束关系图如图1所示,P包含了4个变量,其前缀顺序为∀x∃y∃z∃t,x和y的值域为{1,2,3},而z和t的值域为{1,2,3,4},图中变量用节点表示,两个节点间的边表示两个变量间存在约束关系. 例1的一个解(相容策略树)可用树状形式表示,如图2所示.由于x是全称量词变量,其上一层节点具有多个子节点,而变量y,z和t为存在量词变量,所以上一层的节点只具有一个子节点. Fig.1 Constraint graph of the QCSP in Example 1图1 例1中量词约束满足的问题的约束图结构 Fig.2 A solution tree of Example 1图2 例1的一个解树 首先介绍基本的量词相容性概念,而后提出一个新的相容性概念——全称量词相容性.并讨论了全称量词相容性与量词相容性的关系以及计算复杂度. 量词相容性是从约束满足问题的相容性扩展而来的,它的提出主要是为了化简问题的值域从而加速回溯算法的求解[25],这些量词相容性也被用来识别混合易解子类.给定一个量词约束满足问题,其解树的构造顺序与其量词前缀的变量顺序相关,因此,这里主要关注有向的量词相容性. 定义1(有向的量词弧相容).给定一个二元量词约束满足问题P=(X,Q,D,C),P是有向量词弧相容的,如果对于每个有序的变量对(xi,xj)使得xi≺xj,满足以下条件之一. · ∃xi∃xj:对于每个值a∈D(xi),存在一个值b∈D(xj),使得(a,b)∈R(xi,xj); · ∀xi∀xj:对于每个值a∈D(xi),任意的值b∈D(xj)满足(a,b)∈R(xi,xj); · ∀xi∃xj:对于每个值a∈D(xi),存在一个值b∈D(xj),使得(a,b)∈R(xi,xj); · ∃xi∀xj:对于每个值a∈D(xi),任意的值b∈D(xj)满足(a,b)∈R(xi,xj). 给定一个有序的变量对(xi,xj)使得xi≺xj,如果(xi,xj)满足上述4个条件之一,则(xi,xj)是有向量词弧相容的.下面定义有向量词k相容: 定义2(有向量词k相容).给定一个二元量词约束满足问题P=(X,Q,D,C)和一个自然数k,使得(k≤n).如果对于每个有序的变量集合(y1,…,yk−1,xm),使得yi≺yi+1且yi≺xm(1≤i≤k−1)满足以下条件之一,则P是有向量词k相容的. ·λ1y1,λ2y2,…,λyk−1∃xm对于任意y1y2…yk−1的相容赋值(a1,a2,...,ak−1),存在一个值b∈D(xm),使得(ai,b)∈R(yi,xm)(1≤i≤k−1); ·λ1y1,λ2y2,…,λyk−1∀xm对于任意y1y2…yk−1的相容赋值(a1,a2,...,ak−1),任意一个值b∈D(xm),使得(ai,b)∈R(yi,xm)(1≤i≤k−1). 当k为1时,相容性为量词节点相容;当k为2时,相容性为有向量词弧相容.给定一个二元量词约束满足问题P,如果对于每个自然数i≤k,P是有向量词i相容的,则称P是强有向量词k相容的;如果P是强有向量词n相容的,则P是有向全局相容的.其中,n为变量的数量.如果P是有向全局相容的,则P是可满足的,P的一个解可以按量词前缀的变量顺序通过无回溯地扩展策略树而得到. 为了更好地揭示问题内部隐藏的易解属性,本节深入研究量词约束满足问题的结构性质.不同于经典的约束满足问题,量词约束满足问题的结构特征除了变量间的约束,还决定于量词变量在前缀中的顺序.因此,这里将提出一个新的相容性概念,即全称量词变量相容性,它用于刻画一组存在量词变量和所有的全称量词变量的约束关系.类似于量词相容性,全称量词变量相容性也由一系列的定义组成. 定义3(λ∀相容).给定一个二元量词约束满足问题P=(X,Q,D,C),如果对于每个有序的变量对(λxi,∀xj)使得xi≺xj,且对于每个值a∈D(xi),任意的值b∈D(xj)满足(a,b)∈R(xi,xj),其中,λ是∃或者∀,则称P是λ∀相容的. λ∀相容保证了P是非平凡的,若P不满足该相容性,则全称量词变量存在不可被满足的赋值,所以该问题平凡无解. 定义4(∀量词节点相容).给定一个二元量词约束满足问题P=(X,Q,D,C),如果P是λ∀相容的,且对于任意存在量词变量xi,对于任意的一组X∀(xi)的赋值α,存在一个xi的取值a∈D(xi),使得α与a相容,则称P是∀量词节点相容的. 从定义4可以看出,如果P是∀量词节点相容的,则P中每一变量对(∀xi,∀xj)(xi≺xj)是有向量词弧相容的.类似地,(∀xi,∃xj)和(∃xi,∀xj)也是有向量词弧相容的.但是这并不意味着P是有向量词弧相容,原因在于不能保证P中的(∃xi,∃xj)也是有向量词弧相容的.事实上,将P化简成∀量词节点相容的形式可以删除不支持任何一个量词分支的值. 接下来,定义有向∀量词k相容. 定义5(有向∀量词k相容).给定一个二元量词约束满足问题P=(X,Q,D,C),如果P是λ∀相容的,且对于每个有序的变量集合{y1,y2,…,yk−1,xm},对于任意一个X∀(xm)∪{y1,y2,…,yk−1}的相容赋值αa1a2…ak−1,存在一个ak∈D(xm),使得αa1a2…ak−1ak是相容的,则称P是有向∀量词k相容的. 特殊地,有向∀量词1相容是∀量词节点相容;有向∀量词2相容称为有向∀量词弧相容.类似于量词相容性,强有向∀量词k相容是指对于每个i≤k,P是有向∀量词i相容的;如果P是强有向∀量词r相容的,则它是有向全局∀量词相容的.其中,r是存在量词变量的个数,即r=|X∃|.定义5保证了P中的(∃xi,∃xj)是有向量词弧相容的,所以强有向∀量词弧相容蕴含了有向量词弧相容. 值得注意的是,如果P是有向全局量词相容的,那么P一定是有向全局∀量词相容的,但是反之不成立.这是因为在满足有向∀量词k相容时,可能存在一组存在量词变量的赋值不与任何全称量词分支相容,而对于该赋值,其后续的存在量词变量并不需要存在一个与之相容的值.上述讨论说明,有向全局∀量词相容的限制条件比有向全局量词相容松弛,但这并不影响其保证量词约束满足问题的可满足性. 引理1.给定一个二元量词约束满足问题P,如果P是有向全局∀量词相容的,则P是可满足的. 证明:首先,由于P是∀量词节点相容的,那么第1个变量的值域不为空,因此存在一个相容的1层策略树(包含根节点).不失一般性,这里证明:对于任意的、相容的k−1层相容策略,都可以扩展成一个k层策略.如果第k层变量xk是一个全称量词变量,由于全称量词节点相容蕴含了包含该变量的变量对是量词弧相容的,则xk的任何值都是相容的,所以扩展出的k层策略树是相容的.如果第k层变量xk是一个存在量词变量,若前k−1层包含m个存在量词变量,则m+1≤r(r为全部存在量词变量的数量).又因为P是有向∀量词m+1相容的,所以对于部分策略树中的每一个全称量词分支α,都存在一个xk的值a,使得αa是相容的,因此扩展出的k层策略是相容的.综上,存在一个相容的n层策略是P的一个解,所以P是可满足的.□ 在引理1中,有向全局∀量词相容是P的可满足性的一个充分条件.事实上,如果对于任意的k≤n,前k个变量是有向量词相容的,即可保证P的可满足性.显然,前k个变量的相容性松弛了有向∀量词k相容和量词k相容的约束限制. 本节讨论与有向∀量词相容性相关的算法和计算复杂性,并详细阐述判断其节点相容和弧相容的验证方法.这里首先定义支持集I上的交集算子.设Π={I1,I2,...,Im}为存在量词变量z的一个支持集集合,而Iz是z的一个支持集,交集算子被定义为Π∩Iz={I|I=Ii∩Iz,其中,Ii∈Π}.该算子在产生的新集合中重复的元素被去除,而新集合中可以存在空集元素,即Ø∈Π∩Iz.给定一个存在量词变量z,则全称量词变量集合X∀(z)关于z的支持集集合记为Πz(∀)={I|存在一组赋值X∀(z)=α,使得I是α关于z的支持集}. 基于上述交集算子,我们提出一个计算给定存在量词变量x的全部支持集的算法.该算法采用增量计算的方法,具体过程如算法1所示. 算法1.全称量词变量支持集集合算法. 输入:P=(X,Q,D,C),z是一个存在量词变量; 输出:支持集集合Πz(∀). 算法1输入的问题P需要满足λ∀相容性,而算法过程中不再判断2个全称量词变量之间的约束关系.算法1进行迭代求解,最后返回z的全称量词变量支持集集合.如果该集合中包含Ø元素,则表明存在至少一个全称量词分支,使得z中不存在一个赋值与该路径相容.因此,输入问题P不是有向∀量词节点相容的. 接下来讨论判断一个二元量词约束满足问题有向∀量词节点相容性和有向∀量词弧相容性的方法. a) 对于∀量词节点相容性而言,我们首先需要判断全称量词变量间的相容性,这个过程可以直接判断两个全称量词变量间是否存在约束关系:如果存在且这个约束关系是非平凡的,则可以判定P不是∀量词节点相容的;否则,根据∀量词节点相容性的定义,对于每个存在量词变量x,我们都需要判断每一个全称量词分支是否存在一个x的赋值与之相容,而全称量词的取值组合是随全称量词变量个数指数级增长的,逐个分支判断会导致计算时间是指数级的.但是还可以通过计算x的支持集集合完成这一判断过程.如果支持集集合中包含了Ø,则存在一个全称量词分支不能扩展到变量x,因此P不是∀量词节点相容的;否则,P是∀量词节点相容的. b) 对于有向∀量词弧相容性而言,我们可以使用与∀量词节点相容性同样的方式进行判断.对于每一个存在量词变量对(y,z),我们可以计算Iz(a)的值,计算过程可以通过改造算法1得到.其中,在第11行的对于每个xj的值,首选判断该值是否与a相容:如果相容,则进行交集的计算;否则,尝试下一个值.在计算集合Iz(a)后,我们只需考察集合中是否包含Ø元素:如果包含,则P不是有向∀量词弧相容的.值得注意的是,支持集的集合Iz(a)本身也可能是空集,这是由于没有与a相容的全称量词分支造成的,所以它不是判断不满足有向∀量词弧相容性的依据.若n∀是常数,则有向∀量词弧相容性的判断过程也是多项式时间的. 显然,判断∀量词节点相容性和有向∀量词弧相容性的时间复杂度主要决定于支持集的数量.设L为全部存在量词变量支持集的数量,则不难推出判断有向∀量词节点相容性的时间复杂度为O(LMn),而判断有向∀量词弧相容性的时间复杂度为O(LM2n2). 但在一些特定情况下,支持集的计算过程可以是多项式时间的.这里首先简要介绍BTP(broken-triangle property),它最早是由Cooper等人提出的[24,26],并用来确定约束满足问题中的易解子类.如果一个约束满足问题中的3个变量组成一个有序三元组(x,y,z),如果对于任意一个值对(a,b)∈R(x,y)使得a和b关于z的支持集满足Iz(a)⊆Iz(b)或者Iz(a)⊇Iz(b),则称(x,y,z)满足BTP.在一个二元量词约束满足问题中,若给定一个存在量词变量xk,在xk之前的任意两个全称量词变量x与y有三元组(x,y,z)满足BTP,算法1中的支持集交集运算并不会产生新的支持集,因此计算过程中,|Π[xi,a]|的元素个数的一个上界是d|X∀|,所以Πz(∀)可以在多项式时间内计算. 给定一个二元量词约束满足问题P,如果对于每个存在量词变量z,计算其全称量词关于z的支持集集合都是多项式时间的,则称P满足全称量词支持集易解属性.基于这一属性,在下一节讨论量词约束满足问题的易解子类. 近年来,量词约束满足问题的混合易解子类得到了深入的研究.现有易解子类是基于经典约束满足问题的BTP属性扩展得到的.本节将讨论如何通过全称量词相容性扩展已有的混合易解子类.这里基于BTP,说明全称量词相容性在判断易解子类中的作用. 首先简要说明已知的BTP易解子类.给定一个二元约束满足问题,如果存在一个变量的全序,使得任意3个变量在该序下满足BTP,则可以在多项式时间内判断约束满足问题是否是可满足的.这里只需要将给定的约束满足问题化简为弧相容的形式,如果化简结果不出现值域为空集的变量,则该问题是可满足的.BTP还被扩展到软约束问题中[27],而后被用来识别量词约束满足问题中的易解子类[28].给定一个量词约束满足问题P,P在序≺下满足BTP是指对于P中任意有序三元组(x,y,z)使得x≺y≺z,(x,y,z)满足BTP.由于量词约束满足问题的变量需要按其前缀中的顺序赋值,所以只需判断在该变量序下,量词约束满足问题是否满足BTP即可.定理1确定了基于BTP的量词约束满足问题易解子类. 定理1[28].给定一个二元量词约束满足问题P=(X,Q,D,C),如果P是有向量词弧相容的,且P在其前缀中的变量序下满足BTP,则P是可满足的. 同时,确定一个易解子类不仅需要证明其中包含的量词约束满足问题可在多项式时间内求解,还需证明给定的一个二元量词约束满足问题判别其是否属于该易解子类也是多项式时间的.不难看出,判断P是否为有向量词弧相容的并且是否满足BTP是多项式时间的. 接下来,基于全称量词变量的支持集集合本文提出一个新的混合易解子类,这里首先定义基于支持集集合的BTP性质. 给定一个二元量词约束满足问题P=(X,Q,D,C),x,y和z是3个存在量词变量,Πz(∀)是全称量词变量关于z的支持集集合,如果对于任意值对(a,b)∈R(x,y)和任意的I∈Πz(∀),满足Iz(a)∩I⊆Iz(b)∩I或者Iz(a)∩I⊇Iz(b)∩I,则称三元组(x,y,z)满足uBTP. 定义6(uBTP).给定一个二元量词约束满足问题P=(X,Q,D,C),P中任意存在量词变量组成的三元组(x,y,z)使得x≺y≺z,满足uBTP,则称P满足uBTP. 例2(uBTP的实例):若P是一个二元量词约束满足问题,x,y,z是其中的3个存在量词变量.若z的支持集集合I={{1,2},{2,3},{1,2,4}}并且Iz(x=1)={1,2,3},Iz(y=1)={1,2,4},则(x,y,z)满足uBTP属性;若Iz(x=2)={1,2}并且Iz(y=2)={2,4},则由于Iz(x=2)和Iz(y=2)分别与I中第1个元素取交集后的两个集合不存在包含关系,所以(x=2,y=2,z)不满足uBTP属性. 定理2.给定一个二元量词约束满足问题P=(X,Q,D,C),如果P是强有向∀量词弧相容的,并且P满足uBTP,则P是可满足的. 证明:这里只需证明P是有向∀量词全局相容的,因此采用归纳法证明:对于任意的k>2,如果P是有向∀量词k−1相容的,那么它是有向∀量词k相容的.不妨设P是有向∀量词k−1相容的,β是一个含有k−1个存在量词变量的相容赋值,z是这k−1个变量后的一个存在变量.考虑任意一个包含X∀(z)的赋值α使得αβ是相容的,因为P满足uBTP,则对于β中任意的两个赋值x=a,y=b,有Iz(αa)⊆Iz(αb)或者Iz(αa)⊇Iz(αb).因此在所有的支持集Iz(f)中,f为β中所包含的任意一个赋值,存在一个最小的支持集被所有其他支持集包含,即Iz(c)⊆Iz(f),其中,c是β中的一个赋值.所以存在一个z的取值c,使得αβc是相容的.因此可以得到结论,P是有向∀量词k相容的.又因为P是有向∀量词节点相容的和有向∀量词弧相容的,所以P是有向∀量词全局相容的.根据引理1知,P是可满足的.□ 定理3.给定一个二元量词约束满足问题P=(X,Q,D,C),如果P满足∀量词支持集易解属性,判断P是否满足uBTP可以在多项式时间内完成. 证明:对于任意的由存在量词变量组成的三元组(x,y,z)使得x≺y≺z,如果对于任意的值对(a,b)∈R(x,y)和每个在非空集合Πz(∀,ab)中的支持集I,I∩Iz(a)和I∩Iz(b)存在包含关系,则对于任意的X∀(z)的赋值α使得Iz(α)=I,有Iz(αa)⊆Iz(αb)或者Iz(αa)⊇Iz(αb),因此P满足uBTP.又因为任意的Πz(∀,ab)是多项式时间可以获得的,整个判断过程是多项式时间的.因此,判断P是否满足uBTP是多项式时间的.□ 这里需要解释的是:若集合Πz(∀,ab)为空,则表示不存在一个α使得α与a,b相容,则此种情况不需要进行集合包含的判断. uBTP是对BTP概念的扩展,因此使用uBTP识别的易解子类包含了文献[28]中用BTP识别的易解子类,这里将举例说明满足uBTP的量词约束满足问题. 回顾例1中的量词约束满足问题,显然,该问题不满足BTP.原因是三元组(y,z,t)之间的不等式约束不满足BTP,但是不难验证P满足uBTP,因此可以直接构造P的一个解树而不需要回溯搜索.而uBTP所确定的易解子类是一个更一般化的易解子类形式,它可以囊括更多的易解问题实例. 命题1(uBTP的值约减属性).给定一个二元量词约束满足问题P=(X,Q,D,C)使得P是强有向∀量词弧相容的,并且P满足uBTP,如果α是前k个变量的一组相容赋值,则P(α)是强有向∀量词弧相容的且P(α)满足uBTP. 证明:先证强有向∀量词弧相容,令z为P(α)=(X′,Q′,D′,C′)中的一个存在量词变量,β为P(α)中X′∀(z)的一组相容赋值,因为P满足uBTP,则P(α)是可满足的,所以P(α)中Iz(β)不为空,所以P(α)是∀量词节点相容的.若y为z后的一个存在量词变量,a是z在P(α)中一个取值且βa相容,则由于P是有向∀量词弧相容的,所以在P中存在一个y的取值b,使得αβab相容.由于b与α是相容的,则在P(α)中,b仍是y的一个取值,因此P(α)是有向∀量词弧相容的.再证P(α)满足uBTP,由于P(α)中的变量的值域被约减后并不影响支持集之间的包含关系,所以P(α)仍满足uBTP.□ uBTP的值约减属性说明了变量的赋值过程保持了uBTP及易解性质,为隐蔽集的识别方法的设计提供了理论依据. 易解子类可以将一部分带有特殊约束结构的问题囊括其中,从而证明这些特殊问题是多项式时间可解的.但由于量词约束满足问题本身的计算复杂性,能够被直接证明属于某个已知易解子类的特殊问题是有限的,大量的量词约束满足问题仍属于PSPACE完全的范畴.然而通常情况下,可以在这些问题中识别出一些子结构或子问题属于某个已知的易解子类.为了分析问题中所隐藏的易解结构并分离出易解部分,同时衡量不同易解子类在识别隐藏结构的效果,隐蔽集的概念被提出.它是由Williams等人提出的[18],用于研究SAT的易解子结构,并用于分析SAT求解算法的性能.而后,隐蔽集的概念被扩展到量词布尔范式中[19].隐蔽集是指一个变量的集合,存在一组该变量集合的赋值使得剩余的子问题是可满足的且在多项式时间内可以判定.通常情况下,隐蔽集的研究需基于某一种已知的易解子类.对于SAT而言,易解子类可以是2-SAT(子句长度不超过2的合取范式)或者Horn子句等.隐蔽集的长度影响着求解算法的效率,小隐蔽集意味着求解算法尝试较少的变量赋值即可找到问题的解. 根据SAT和量词布尔范式中的隐蔽集的定义,本文给出量词约束满足问题的隐蔽集定义. 定义7(隐蔽集).给定一个量词约束满足问题P,若存在一个部分策略树Ti,使得对于该树中任何分支对应的赋值α,存在一个多项式时间的算法返回P(α)的一个解,则称P的前i个变量是P的一个隐蔽集. 若已知一个量词约束满足问题的隐蔽集,求解该问题则简化为寻找一个满足隐蔽集定义的部分策略树Ti,其计算复杂度与i值相关,而问题的变量数量只影响计算复杂度的多项式部分.因此,隐蔽集的存在降低了求解算法的计算时间. 显然,本文提出的uBTP易解子类和已知的BTP易解子类可以用于识别隐蔽集.为了研究本文提出的混合易解子类对隐蔽集的影响,我们将分析使用不同易解子类时隐蔽集的大小,即隐蔽集中变量的个数. 本文基于量词约束满足问题求解器QCSP-Solve[5]分析隐蔽集的大小.QCSP-Solve是一个基于回溯算法的完备的量词约束满足问题求解器,它可以求解二元问题.同时,QCSP-Solve中还加入了诸多在CSP求解中使用较为成熟的技术.例如,基于冲突的回跳技术[29]在产生冲突赋值时,会分析失败的原因,并回跳至产生冲突变量对应的层.这种技术不同于一次只回溯1层的普通回溯算法,它可以大幅度减少不必要的搜索空间.在预处理过程中,QCSP-Solve使用了量词弧相容算法QAC-2001[30]和对称消除策略等技术,用于加速求解器的效率. 在实验分析中,本文改造了QCSP-Solve中的算法,在回溯搜索的基础上加入了易解子问题的识别过程.在展开每个节点并对变量赋值后,算法调用识别算法,判断后续未赋值变量间是否满足BTP(uBTP)属性,从而识别出易解子问题.若未赋值变量属于给定的易解子类且是可满足的,则表明当前的量词分支可以构成隐蔽集对应的部分策略树的一个分支,因此算法回溯并尝试下一个量词分支.否则继续尝试下一个未赋值的变量.当算法找到问题一个解树时,根据命题1的结论,uBTP易解子类中的一个问题实例P在对前i个变量赋值为α后,其剩余的子问题P(α)仍然满足有向∀量词弧相容和uBTP.所以在回溯搜索过程中,具有最多变量赋值的量词分支的长度即为所找到的隐蔽集的大小.但是找出某个量词约束满足问题的全部隐蔽集需要遍历整个解空间,这对于PSPACE完全类中的问题是十分困难的,而计算最小的隐蔽集也是困难的.因此,本文只分析找到第1个解时隐蔽集的大小. 本节通过实验分析隐蔽集大小.分析隐蔽集大小的实验采用一系列随机生成的量词约束满足问题作为测试实例.所有实验采用一台工作站进行,其中,CPU为E5-1650v4,内存为16GB,Windows Server 2016作为操作系统.实验算法采用C++编写,并将检测隐蔽集的代码与QCSP-Solve算法结合,实验系统采用Visual Studio 2010编译.本节首先介绍量词约束满足问题的生成模型,然后分析实验结果,比较不同约束密度的情况下,两个混合易解子类的隐蔽集大小,以及QCSP-Solve在回溯搜索过程中找到易解部分时未赋值变量个数平均值. 在衡量量词约束满足问题的算法效率时,随机生成的问题实例通常被作为测试基准.使用最多的随机生成模型是Model B[31].该模型最早用于生成约束满足问题,其改进的版本具备了精确的可满足性相变点,称其为Model RB[32].而后,量词约束满足问题也使用此类模型作为测试基准. 在约束满足问题的Model B中,4个参数被用来控制生成问题的规模和难度,所以通常用四元组(n,d,p,q)表示,其中,n为变量的个数,d为每个变量值域的大小,p为约束的密度参数,它控制问题中约束的数量. 模型从n(n−1)/2个可能的二元约束中均匀地随机地选取|pn(n−1)/2|个约束,q为约束的松紧度参数.对于每个二元约束模型,将均匀地随机地选取qd2个值对设为允许的关系元组.对于量词约束满足问题,还需要额外的3个控制参数,n∀指定了全称量词变量的个数,q∀∃和q∃∃被用来取代q,q∀∃表示一个全称量词变量和一个存在量词变量之间的约束松紧度,q∃∃表示两个存在量词变量之间的约束松紧度. 另外,全称量词变量在前缀中的排列位置也会影响量词约束满足问题的约束结构.在本文的实验中,两种排列方式将被采用.第1组中,n∀个全称量词变量的位置是随机选择的;第2组中,全称量词变量和存在量词变量被划分到变量块中,两种变量块交替排列. 但是研究指出,量词约束满足问题的生成模型存在平凡不可满足的缺陷(flaw issue)[31].如果n∀足够大且q∀∃过小,则生成的问题中会存在某个全称量词分支,使某个存在量词变量中没有相容的赋值,这样导致了所生成的问题是平凡无解的.为了解决这一缺陷,Gent等人提出了基于双映射的结构化约束关系元组生成方案,代替完全随机的生成模型.但是结构化的生成方案破坏了随机均匀地值对选取规则,而且这种方案使得90%以上的值对都是允许的关系元组,即q∀∃大于0.9.事实上,如果控制q∀∃在0.9以上,平凡不可满足的缺陷发生概率是极低的.因此在本节的实验中,q∀∃的取值为0.95. 本节实验对比BTP易解子类和uBTP易解子类确定量词约束满足问题中的隐蔽集大小的效果. 首先分析第1组实验.在生成实例时,变量的顺序随机排列.这里取n=20,d=10,而n∀的取值分为两种情况,n∀=6和n∀=8.约束密度参数p的值从0.2递增到0.5,增量为0.025.当p=0.2时,约束关系图的密度较为疏松,所生成的问题实例较为简单;而p=0.5时,约束图密度增大,约束增多,问题实例的求解难度也随之增加.对于每个p值,q∃∃的值从0.7递增到0.9,增量为0.05,共5个取值,以生成不同难度的约束关系.q∃∃值越小,相容的赋值就越小.而当q∃∃过小时,生成的实例可能是不可满足的,因此q∃∃的值最小为0.7,以保证部分生成的实例是可满足的.对于每组p和q∃∃的取值,生成20个实例,并计算它们的隐蔽集大小. 表1列出了n∀=6时的实验结果,表2列出了n∀=8的结果. Table 1 Comparison of the backdoor size detected by BTP and uBTP (n∀=6)表1 BTP与uBTP的隐蔽集大小的对比结果(n∀=6) Table 2 Comparison of the backdoor size detected by BTP and uBTP (n∀=8)表2 BTP与uBTP的隐蔽集大小的对比结果(n∀=8) 对于每个p值,计算q∃∃的5个取值的100个实例求解到的隐蔽集大小的平均值,同时还统计了QCSP-Solve在回溯搜索过程中找到易解部分时未赋值变量个数平均值.从表1和表2中可以看出,随着p值的增大,问题实例的难度也随之增加.由于约束数量增多,在回溯过程中赋值后,剩余的变量构成一个易解问题的可能性变小,所以求解到的隐蔽集的规模随p值增加而增大.而对于所有p值,使用uBTP作为易解子类的隐蔽集规模比BTP小,这一结果与uBTP易解子类包含BTP易解子类的事实相符,所以uBTP应识别到更小的隐蔽集.而对于简单问题(p值较小时),规模差别更大一些,uBTP的隐蔽集更具有优势.而对于每个p值平均搜索深度略小于隐蔽集大小,uBTP的平均搜索深度也小于使用BTP时的平均值.这意味着uBTP减小了回溯搜索过程所展开的节点数量.随着n∀的增加问题变难,所以隐蔽集规模略有增加.但是对于约束密度较大时,两种易解子类的效果不明显. 接下来分析第2组实验.同样取n=20,d=10.而全称量词变量的排列不再是随机的,而是结构化的.每个全称(存在)量词变量块包含1个(2个)全称(存在)量词变量,全称量词变量块和存在量词变量块交替出现,并设定n∀=6,前缀中变量的顺序是:2个存在量词变量,然后1个全称量词变量,以此类推.p的取值范围为0.2~0.5,q∃∃的值为0.7~0.9.对于每个p,100个实例的平均值被计算.表3列出了该组实验的结果.与前一组结果类似,uBTP可以识别到更小的隐蔽集,而这种优势在低密度约束问题中体现得更加明显. Table 3 Comparison of the backdoor size detected by BTP and uBTP (alternative blocks)表3 BTP与uBTP的隐蔽集大小的对比结果(变量块交替) 约束满足问题可解子类的研究可以追溯到20世纪80年代.Freuder首先指出:如果一个约束满足问题的约束图是树形结构,则存在一个不需要回溯的算法在多项式时间内求解该问题[33].而后,易解子类的研究逐步兴起.一方面,利用约束图结构的特性识别易解子类和分析计算复杂度[34−36];另一方面,研究约束关系的特征也是一个重要的确定可解子类的方法.这方面的研究主要集中在约束语言和约束关系的代数学方法上.例如,Bulatov等人研究了有限域上的复杂性分类[37].混合易解子类是最近几年提出的一种全新的识别易解子类的技术.它结合了结构子类和关系子类的特点,同时限制约束图的结构和每个约束中的允许的元组关系,从而得到更一般化的易解子类. 一个代表性的混合易解子类是Cooper等人提出的BTP概念,他们通过一般化树形结构并限制3个变量之间的约束关系,得到了约束满足问题上的混合易解子类[24].基于BTP的混合易解子类是基于树状约束结构子类更一般化的性质,通过加入约束关系的限制,使得树状结构的特征这一限制条件可以适当地放宽,因此,该易解子类在增加元组关系限制的同时放松了对结构的限制条件,从而得到比树状约束结构子类更一般化的结论.因此,BTP子类可以囊括更多的易解情况.BTP定义了3个变量间的约束关系,而更多的变量间的关系也被讨论.例如,Cyril等人提出了Extendable-Triple Property(ETP)[38],定义了4个变量间的性质.BTP的概念还被扩展到约束优化问题中,与之对应的是Joint-winner属性[27].该属性同样定义了3个变量之间的约束元组关系,符合该属性的软约束问题是多项式时间内可解的.一个更一般化的结果是Naanaa提出的Rank CSPs[39].该子类利用集合论中秩的概念,计算支持集的集合中,若干支持集取交集的秩.基于Rank CSPs的易解子类被证明包含了诸多已知的混合易解子类,例如BTP、ETP、行凸属性Row convexity[40]和m-tight[41]约束属性等.但是BTP具有比其他易解子类更多的性质,例如BTP在弧相容算法约减后仍满足BTP.而类似的性质,其他混合易解子类并不具备,ETP在路径相容约减运算时(3个变量间的相容性)下并不是封闭的.Cohen等人还深入研究了更多的混合可解子类的情况,并提出了二元约束满足问题上的复杂性分类定理[42]. BTP易解子类以及其他的混合易解子类还用于变量的消元中[43].若存在一个变量全序使得最后的一些变量满足BTP,则这些变量是可以被消元的.但是给定一个约束满足问题,寻找含有变量数最多的子集使得子集中的变量在某个变量顺序下满足BTP属性却是NP难的.基于BTP,更多的用于变量消元的微结构被识别出来,但是这些结构具有十分复杂的元组关系[44].另一方面,基于BTP的值合并技术也被提出[45].该技术可以对约束满足问题进行化简,在保证问题可满足性不变的情况下,合并具有相似结构的值,从而化简问题的规模.基于BTP值合并技术一个混合易解子类也被提出. BTP描述了二元约束之间的关系,为了描述二元以上的约束满足问题,对偶的BTP被提出[46],一个多元约束满足问题可以转化成对偶的二元形式,即将约束映射成变量,值域为约束中的元组关系,从而在其对偶的问题上定义BTP以确定多元问题的易解结构.另外,BTP还应用于识别隐含的易解结构,Mouelhi等人研究了在不同相容性等级下,BTP易解子类涵盖各类约束满足问题的能力[47],并指出,高阶相容性可以将更多的约束满足问题确定为是多项式时间可解的. 对于量词约束满足问题易解子类的研究,目前主要的思路是扩展经典约束满足问题的易解子类.例如,在20世纪70年代就证明了量词布尔范式实例中,若子句的长度都是2则是多项式时间内可解的[48],基于Horn子句的量词布尔范式实例也是多项式时间内可解的[49].但是这种方法却面临很大的挑战,原因在于:全称量词很大程度上改变了约束结构,原有的易解子类在量词约束满足问题中并不一定成立,因此还需要考虑更多的限制条件.通过这样的思路,首先,基于结构特征的易解子类被确定出来,Gottlob等人研究了全称量词受限情况下基于结构的易解子类[50];其次,Chen等人深入分析了结构易解子类的特征,还分析了基于约束关系的易解子类的相关性质[51];更进一步地,Börner等人分析了更多的基于约束关系的可解情况和博弈游戏中多项式时间可解的问题[52];另外,混合方式的结构分析技术也被应用在量词约束满足问题中[28]. 易解子类的另一个重要的应用是识别隐蔽集[18].所谓的隐蔽集是约束满足问题中的一个变量子集,并且存在一个多项式时间的算法,使得该算法可以求解剩余的问题.换言之,在对隐蔽集中的变量赋值后,剩下的子问题是多项式时间可解的.例如,环割集事实上就是一个隐蔽集,在去除环割集中的变量后,余下的约束图结构是无环的,这使得余下的子问题可在多项式时间内求解.利用这一性质,李占山等人研究了基于环割集的约束满足问题结构分解技术和相关的约束传播算法[53−55].Kilby等人[20]通过实验分析得出,问题求解难度和隐蔽集的大小间存在着密切的关系.而Ruan等人[21]也研究了隐蔽集对问题结构和求解难度的影响,并指出:当隐蔽集足够小时,存在多项式时间算法可以求解该问题.研究者还根据隐蔽集的概念和相关性质,提高了约束满足问题求解算法的效率.因此,基于何种易解子类,决定了隐蔽集的识别效率和求解算法的效率.诸多易解子类都被用于识别隐蔽集中,例如在SAT问题中,主要使用了2-SAT和Horn子类;Misra等人讨论了隐蔽集的上界和下界性质[56];Samer等人讨论了量词布尔范式中的隐蔽集的复杂性[19].基于约束关系的易解子类也被应用于隐蔽集的识别中,而利用混合易解子类的变量消元技术本质上也可以被看作是一个寻找隐蔽集的过程.因此,易解子类的研究为隐蔽集的识别和搜索算法的设计提供了理论基础. 本文深入研究了量词约束满足问题中的约束关系及混合易解子类所需要的条件,并提出一个新的量词约束满足问题的混合易解子类.正如我们所知:由于全称量词变量的引入,量词约束满足问题结构性质不同于其对应的约束满足问题.因此,本文提出的方法将量词约束满足问题易解子类的识别分为两部分:在第1部分中,我们分析一个存在变量与全称量词变量的约束关系和相容性关系,并提出全称量词相容的概念,同时讨论了多项式时间的全称量词变量相容性判别的情况;在第2部分中,在全称量词相容的情况下,分析存在量词变量之间的约束关系,并在原有的BTP混合易解子类基础上一般化其限制条件,提出uBTP的概念,从而达到扩展易解子类的目的.同时,本文的易解子类识别方法还可以应用在扩展其他混合易解子类之中,由于ETP、Row convexity属性和Rank CSP与BTP有类似的性质,所以还可以利用本文的方法通过扩展这些性质得到诸多一般化的理论结果,其中的Rank CSP定义在非二元约束上,而该方法对非二元问题中易解子类的识别也是有效的.本文还将混合易解子类应用到识别隐蔽集中,并分析不同易解子类所确定的隐蔽集的大小.通过实验验证了所提出的易解子类在识别隐蔽集方面比原有子类更具优势,同时还可以减少回溯算法中搜索树的平均深度,以达到减小搜索空间的目的.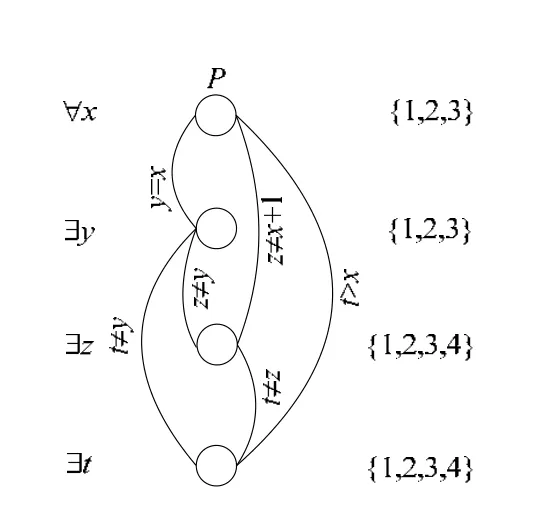
2 全称量词相容性
2.1 量词相容性
2.2 全称量词相容性
2.3 全称量词相容性算法

3 易解子类
4 隐蔽集的识别
5 实验分析
5.1 生成模型
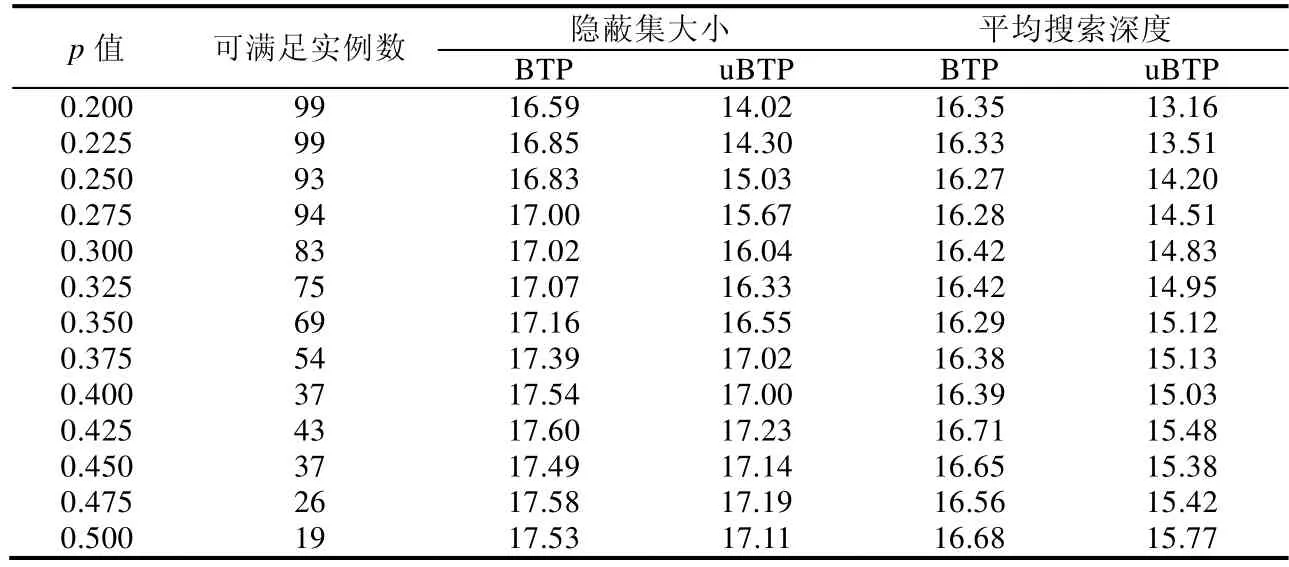
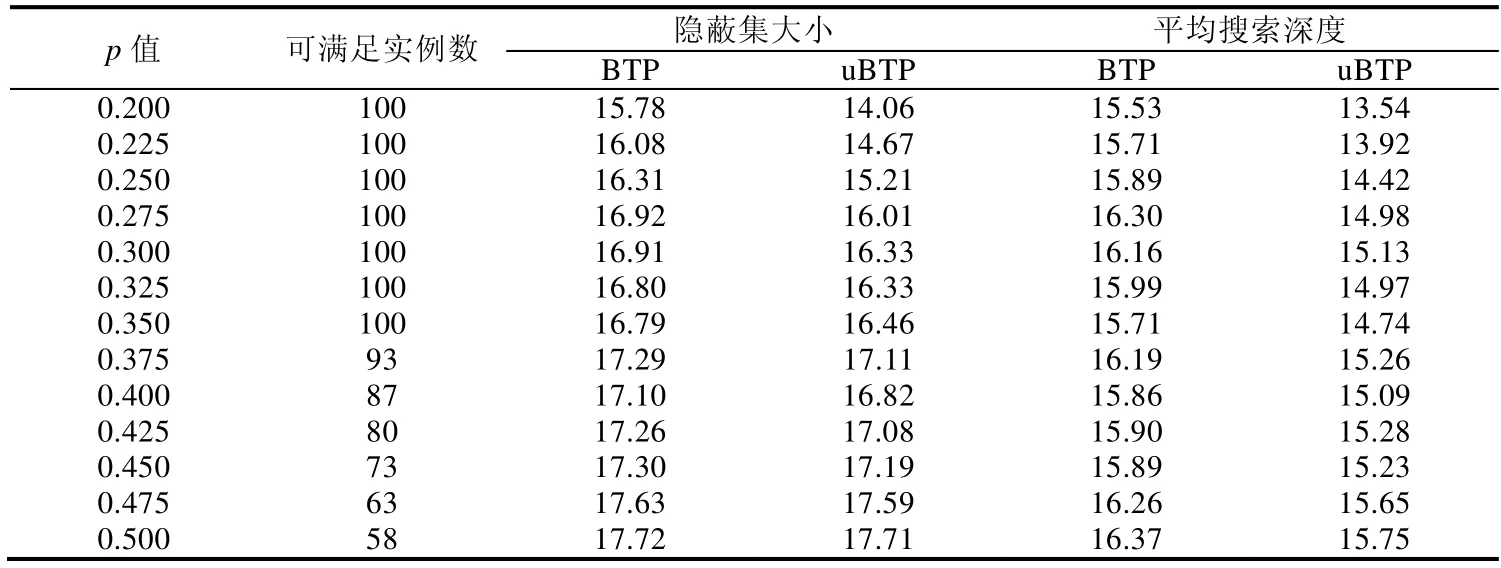
5.2 实验结果

6 相关工作
7 总结
