混合个体选择机制的多目标进化算法∗

2019-10-26陈晓纪周爱民

软件学报 2019年12期

陈晓纪，石川，周爱民，吴斌

1(北京邮电大学计算机学院，北京 100876)

2(邢台职业技术学院信息工程系，河北邢台 054000)

3(华东师范大学计算机科学与软件工程学院，上海 200062)

多目标优化问题(multiobjective optimization problem，简称MOP)是指那些同时优化多个目标的问题.一般来说，这些单个目标是相互冲突的，而且总体目标没有单个最优解[1].求解多目标优化问题常常是困难的，它不像单目标优化问题(single objective optimization problem，简称SOP)那样只有一个最优解，多目标优化问题得到的是一组最优解.因为进化算法(EAs)是基于种群的优化算法，能够多次迭代优化逼近MOP的Pareto前沿，所以进化算法(EAs)广泛应用于解决MOP问题[2].这些EAs被称为多目标进化算法(MOEAs).近年来，大量MOEAs被提出，这些算法可以分为3类[1]:基于Pareto支配的算法[3−6]、基于指标的算法[7−9]和基于分解的算法[10，11].MOEA/D[10]是最近最具代表性的基于分解的算法，其基本思想是:将MOP分解为一组标量目标子问题.相邻子问题相互协作产生新的后代解集，而新产生的解不仅会更新相应子问题，也会更新相邻子问题.通过这种方式，所有子问题同时被优化，最终，所有子问题的解集构成了原始MOP的Pareto解集(PS)与Pareto前沿(PF).

后代选择是MOEA的核心问题之一[12]，后代选择显著地影响了迭代优化的收敛速度和解集的多样性.目前主要有3种后代选择方式.

(1) 非支配排序是一种非常流行的方法.对于多目标优化问题，通常存在一个解集，这些解之间对于所有目标函数而言是无法比较优劣的，其特点是无法在改进任何目标函数的同时不削弱至少一个目标函数.它根据解之间的支配关系对所有解进行排序，称其为非支配排序.典型的非支配排序算法包括NSGA-II[4]和SPEA2[5].非支配排序方法往往不适用于代价昂贵的多目标优化问题；

(2) 代理也是选择后代最优解的常用方法.代理模型是指计算量小、但其计算结果和高精度模型的计算分析结果相近的分析模型.在优化设计时，可以用代理模型替代高精度分析模型.典型的利用代理模型解决多目标优化问题的算法包括MOEA/D-EGO[13]和MOEA/D-RBF[14].通常，利用某些方法获取的样本点集构造代理模型往往需要拟合复杂的数学模型，这个过程是非常耗时的.同时，为了保证代理模型具有较高的精度，代理模型需要优化许多参数[15]；

(3) 最近，分类也成为选择后代最优解的常用方法.分类就是按照某种标准给对象设置标签，再根据标签来区分归类.分类算法利用有监督机器学习方法构造分类器，用于后代选择.典型的分类算法包括MOEA/D-CPS[16]，CPS-MOEA[12]和MOEA/D-SVM[17].分类算法将后代选择看成是一个分类问题.然而，分类后优良解的数量往往不止一个，利用随机选择方式很难从优良解集中获取最优解.此外，构建复杂分类器往往存在优化参数耗时等问题.

考虑到现有后代选择方式的缺陷，本文提出了一种融合分类与代理的混合个体选择机制；进一步基于经典的MOEA/D框架，利用混合个体选择机制设计了新的多目标进化算法，称为MOEA/D-CS(MOEA/D based on classification and surrogate).由于分类能够以较小的时间代价提升算法性能以及代理能够较为准确地估计目标值，有许多工作利用分类或者代理实现后代选择.但是单独利用分类或者代理存在上述缺陷，本文融合二者的优点实现了一种混合个体选择机制.在混合个体选择机制实现过程中，首先利用分类器过滤候选解并且只有优良解被保留下来；然后利用轻量级代理模型估计优良解的目标值；最后，利用目标值排序策略获得最优解.在19个具有2目标或3目标的多目标优化测试函数上，本文比较了MOEA/D-CS算法与其他多个当前流行的基于分解多目标进化算法.实验结果表明:在没有显著增加时间代价的情况下，MOEA/D-CS算法在绝大部分测试函数上取得了最好的性能.

本文第1节介绍相关工作.第2节介绍算法实现的细节.第3节进行大规模实验，并对实验结果和敏感性参数进行深入分析.第4节总结全文，并对未来的研究工作进行阐述.

1 相关工作

在过去的二十几年时间里，各种多目标进化算法相继被提出.总体来说，多目标进化算法主要包含3类.

· 第1类算法的特点是基于个体支配关系与精英保留策略.David等人[18]设计的多目标进化算法VEGA被认为是利用进化算法解决多目标优化问题的先驱工作.Srinivas和Deb[19]提出的NSGA奠定了多目标进化算法的基本框架.NSGA-II[4]是NSGA的改进版本.NSGA-II使用精英保留策略，保留最好的父代个体和子代个体.Zitzler和 Thiele[20]提出的SPEA利用外部种群实现精英保留策略.SPEA的改进版本SPEA2[5]也相继被提出.SPEA2[5]使用最近邻密度估计来实现更高搜索效率，新的归档截断方法保证边界解被保留下来；

· 第2类算法的特点是使用指示器指导搜索过程.Zitzler和Künzli[7]首先提出了一种基于指标的进化算法(IBEA).在IBEA中，不需要任何额外的多样性保留机制.与其他MOEAs相比，IBEA只比较成对的个体而不是整个近似集.Basseur和Zitzler[8]提出了一个以指标为基础的处理不确定性问题的模型，其中每个解在目标空间中被分配一个概率.Bader和Zitzler[9]提出了一种基于快速超体积的MOEA算法，该算法用于处理多个目标的优化问题.为了减少超体积计算的开销，提出了一种基于蒙特卡罗模拟的快速估计超体积近似集的方法；

· 第3类算法使用分解和降维[21]来解决多目标优化问题.这个类型的典型算法是MOEA/D[10，11].这种方法将MOP分解为一组子问题并同时优化这些子问题.后代繁殖和环境选择都是基于子问题的.

伴随着多目标进化算法的发展历程，多目标进化算法在理论研究方面也取得了一定的进展.在一个基于种群的多目标问题上，Laumanns等人[22]首次分析了算法的运行时间.在某些多目标优化问题上，Laumanns等人[23]证明了基于特定种群的多目标优化算法具有较低的运行时间以及算法运行时间与Pareto前沿是密切相关的，而且算法总的运行时间是有界的.Qian等人[24]从理论上研究了重组算子对多目标进化算法的影响.在一系列多目标优化基准问题上，结合重组算子的多目标进化算法不仅可以缩短算法的运行时间，而且能够使最优解集更靠近Pareto前沿.

利用多目标进化算法解决多目标优化问题，如何选择后代个体是关键.在多目标进化算法中，主要有3种后代选择方式.

(1) 传统的算法使用非支配排序[4，5]选择后代解集.NSGA-II[4]算法首先利用非支配排序找出种群中的非支配解；然后，一部分非支配解通过交叉与变异生成子代解，并且利用实际目标值评价每一个子代解；最后，整合父代种群与子代种群，利用非支配排序保存下一次迭代优化需要的种群.SPEA2[5]算法除了采用传统的交叉与变异产生子代解，还利用非支配排序与密度估计方法计算个体的适应值，算法精度要高于NSGA-II[4]；

(2) 近年来，许多文献利用代理选择后代最优解.文献[25，26]利用回归或排序技术用来构建代理模型，这样可以减少目标值评价的次数.文献[27]使用代理模型进行局部搜索和预选择.MOEA/D-EGO[13]利用高斯随机过程解决代价昂贵的多目标优化问题.MOEA/D-EGO[13]利用高斯过程为每个目标分别建模，然后获得每个分解子问题的模型.但是MOEA/D-EGO[13]利用种群的聚类信息建立代理模型，没有考虑种群的整体信息对代理模型精度的影响，这可能导致算法的精度较低，而且需要调整较多参数.同时，利用局部信息更新代理模型可能导致错误的搜索.文献[14]利用集成的径向基函数网络构建代理模型MOEA/D-RBF[14]，它保持了固定大小的训练集，但是只针对较小的种群规模和迭代次数；

(3) 最近，随着机器学习算法的广泛应用，有监督分类算法已经成为选择后代最优解的常用方法.Yu等人[28]提出了RACOS算法，该算法利用分类模型对优良解与不良解进行分类.RACOS算法在处理高维优化问题时具有明显的优势.Zhang等人[16]提出的MOEA/D-CPS算法利用非支配排序和KNN[29]构造分类器模型，在具有复杂Pareto前沿的多目标优化问题上取得了较好的性能.Zhang等人[12]利用非支配排序和CART[30]构造分类器模型，与NSGA-II[4]算法结合，提出了CPS-MOEA算法，在大量多目标优化测试函数上取得了较好的性能.Lin等人[17]利用SVM[31]训练分类器，提出了MOEA/D-SVM算法，提升了MOEA/D的性能.

然而，上述后代选择方式普遍存在着时间代价较高、难以准备准确的正例和负例样本或者很难保证代理模型的精度.因此，往往不适用于代价昂贵的多目标优化问题.

2 MOEA/D-CS算法

后代选择是多目标进化算法中一个非常重要的问题.不同于以往的后代选择方式，本文融合分类与代理的混合个体选择机制获取最优解，基于混合个体选择机制设计了新颖的多目标进化算法.本节首先简单介绍基本的MOEA/D框架；然后详细论述融合分类与代理的混合个体选择机制的具体实现过程，包括如何利用非支配排序策略[4]与k近邻(KNN)[29]算法构建有监督分类器模型以及相似性度量方法构建轻量级代理模型；最后介绍本文设计的融合分类与代理个体选择机制的MOEA/D-CS算法框架及其时间复杂度.

2.1 基于分解的多目标进化算法框架

MOEA/D将MOP问题分解为一组子问题{g1，g2，…，gN}，并且同时优化这些子问题.每个子问题的最优解有可能成为MOP问题的Pareto最优解[32].本文使用切比雪夫(Tchebycheff)方法作为MOEA/D的分解方法.每个子问题i被定义为

2.2 融合分类与代理的混合个体选择机制

在基于分解的多目标进化算法中，如果每个子问题产生的后代候选解越多，那么获得最优解的几率就越大，但是计算多个后代候选解花费的时间代价也越高.因此，传统方式利用实际目标值评价不适用于这类问题.目前，基于分类与代理获取最优解的相关算法越来越多.分类算法普遍存在着如下问题:难以构造准确的分类器模型；利用局部信息构建的代理模型精度难以保证；而利用全局信息构建的代理模型虽然精度较高，但是需要花费的时间代价太大.鉴于单独利用分类与代理获取最优解存在的诸多问题，本文提出了融合分类与代理的混合个体选择机制，实现从后代候选集中选择最优解，在没有显著增加时间代价的前提下，提升了获取最优解的概率.

下面详细介绍融合分类与代理的混合个体选择机制实现过程.

· 首先，使用k近邻(KNN)[29]构建分类器[16].

设置〈x，y〉为一组训练数据，其中，x是数据点的个体向量，y∈L是数据点对应的标签，L是一组标签集合.个体向量与标签之间的对应关系可以表示为y=Class(x).训练分类器的目的是找到一个关系基于训练数据集可以近似地表示实际的对应关系y=Class(x).

本文引入两个外部种群P+和P−，P+包含了迄今为止发现的标签为+1的优良解集合，P−包含了标签为−1的不良解集合.为了获得P+和P−，本文使用非支配排序策略[4].令q=NDS(p，n)表示该方法从p中选择最好的n个解存储在q中，这里所指的“最好的n个解”包含3种情况.

(1) 非支配解的数量等于n，最好的n个解就是全部非支配解的集合；

(2) 非支配解的数量大于n，算法利用拥挤距离[4]过滤掉多余的非支配解；

(3) 非支配解的数量小于n，此时根据序关系和拥挤距离[4]从支配解中找出一部分最靠近Pareto前沿的解，再与非支配解集组成最好的n个解.

令P为初始种群，N为种群P的大小.P+和P−被初始化为

设x是一个个体向量，L={+1，−1}，其中，+1是优良解的标签，−1是不良解的标签.本文使用k近邻(KNN)[29]作为分类算法.其中，k近邻(KNN)[29]的训练数据包括当前整个种群P:

N(x)表示训练集中与x最近邻的K个邻居个体，K设置为奇数.sign(x)的执行过程为:从N(x)中依次选择个体向量t，将个体向量t对应的标签yt累加求和，累加求和的结果只能是正数或负数.此时，如果累加求和的结果为正数，sign(x)返回+1，则x标记为优良解；否则，sign(x)返回−1，x标记为不良解.

令Q表示每一代中新产生的一组最优解集合，Q+和Q−分别表示包含非支配和被支配关系解集.然后，P+和P−按照如下方式进行更新:

· 其次，利用相似性度量方法构建轻量级代理模型.

传统的代理模型时间代价较高，往往不适用于代价昂贵的多目标优化问题.本文构建了一个轻量级代理模型，能够以较小的时间代价保证代理模型具有较高的精度.文献[35，36]指出，连续MOP问题在决策空间PS可以定义为分段连续的流形结构，那么对于MOP来说，目标空间PF也应该是分段连续的.因此，连续多目标优化具有如图1所示的性质.图1(a)展示了PS与PF之间的对应关系.图1(b)中，x1，x2，x3∈D(决策向量空间)，z1，z2，z3∈F(D)(目标向量空间)，相比x3，x1与x2更接近，因此z1与z2也就更接近.同理，对于D中的任意两个相近的解，相应的F(D)中目标值也应该越相近.

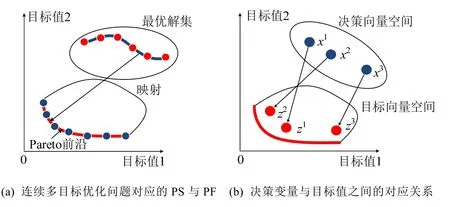
Fig.1 Characteristics of continuous multiobjective optimization problem图1 连续多目标优化问题的性质

由于每个子问题的后代候选解都是由其邻域个体通过DE[33]算子和多项式变异[34]生成的，并且执行分类操作后只有优良解被保留下来.因此，本文利用相似性度量方法计算每个优良解与对应邻域个体之间的相似性，利用最近邻域个体的目标值作为每个优良解的估计目标值.目前，有许多方法用来度量相似性.本文利用余弦相似性度量每个优良解与邻域个体之间的相似程度.余弦相似性主要利用向量空间中两个向量的余弦夹角进行计算.余弦相似性的计算公式如下:

x1和x2表示向量空间中具有相同维度的两个向量，sim(x1，x2)越接近1，x1和x2就越相似.

2.3 算法框架与分析

MOEA/D-CS算法框架如图2所示.MOEA/D-CS算法流程主要包括4部分.

1) 初始化工作:生成每个子问题对应的个体xi，邻域信息Bi，初始化理想点z*(第1行)；

2) 利用非支配排序[4]获取正例P+和负例P−样本，训练有监督分类器模型(第3行)；

3) 循环选择每一个子问题:首先，利用classifier对候选解进行分类(第6行)；然后，如果条件满足，则利用轻量级代理模型估计每个优良解的目标值并保存最优解(第7行～第13行)；最后，更新理想点z*和种群P(第14行)；

4) 更新正例P+和负例P−样本(第16行).

Fig.2 MOEA/D-CS algorithm framework图2 MOEA/D-CS算法框架

针对MOEA/D-CS算法的每一个子问题，其时间复杂度主要包含3部分.

1) 利用非支配排序[4]将初始种群划分为正例P+和负例P−样本.非支配排序[4]算法的时间复杂度是O(mN2)，其中，m是目标个数，N是种群大小；

2) 利用有监督分类器执行分类操作.对于每一个后代候选解，它需要与分类器中的每个样本计算欧式距离.因此比较次数是N，所以时间复杂度是O(MN)，其中，M是后代候选解的数量；

3) 利用余弦相似性计算每个优良解与邻域个体的相似程度.邻域个体的数量上限是N，M是优良解数量的上限，每个优良解最多需要计算N次，所以时间复杂度是O(MN).

本文主要针对2目标或3目标，每个子问题的后代候选解数量M=3，所以有m≤M.因为MOEA/D-CS算法需要同时优化N个子问题，所以MOEA/D-CS算法的时间复杂度为O(mN3)+O(MN2)+O(MN2)，近似为O(MN3).本文以函数评价次数作为终止条件，这里假设函数评价次数为C，那么终止条件折合成迭代次数就是C/N.所以MOEA/D-CS算法总的时间复杂度近似为O(CMN2).

3 实验

3.1 实验设置

为了验证MOEA/D-CS算法的有效性，将其与当前多个有代表性的MOEA算法进行对比实验.

1) MOEA/D-CPS[16].MOEA/D-CPS[16]首先利用DE[33]算子和多项式变异[34]为每个子问题生成3个后代候选解，然后利用有监督分类器执行分类操作；

2) MOEA/D-DE[11].MOEA/D-DE[11]利用DE[33]算子和多项式变异[34]为每个子问题生成1个后代解；

3) MOEA/D-MO[37].MOEA/D-MO[37]首先利用DE[33]算子和多项式变异[34]为每个子问题生成3个后代候选解，然后直接利用实际目标值函数评价每个后代候选解；

4) MOEA/D-SIM.为了对比仅使用代理模型的后代个体选择机制，本文设计了 MOEA/D-SIM算法.MOEA/D-SIM首先利用DE[33]算子和多项式变异[34]为每个子问题生成3个后代候选解；然后，利用余弦相似性度量每个后代候选解与邻域个体的相似性；最后，将最近邻域个体的目标值作为当前后代候选解的估计目标值.

本文采用文献[38]中使用的9个多目标优化测试函数F1～F9与文献[39]中使用的10个无约束多目标优化测试函数ZZF1～ZZF10.

本文使用IGD[36]指标评价算法的性能.令P*是一组沿着PF均匀分布的点，P在目标空间中近似于PF.IGD[36]定义为

其中，d(v，P)是v和P中任何一点的最短欧氏距离；|P*|表示P*的基数，如果P*足够大，它就可以更好地表示PF*；IGD(P*，P)同时衡量P的收敛性和多样性，IGD(P*，P)指标越小，P就越接近于PF*.在本文的实验中，对于2目标函数，从PF*中选择500个均匀分布的点代表PF*.对于3目标函数，选择990个均匀分布的点代表PF*.

3.2 有效性实验

本文分别在F1～F9和ZZF1～ZZF10测试函数集上做了对比实验.所有算法均独立运行30次.在每个测试函数上，分别计算每种算法的IGD均值和标准差.IGD均值越小，说明算法的收敛性和多样性越好；标准差越小，说明算法稳定性越好.同时，本文还分别统计了每种算法在F1～F9和ZZF1～ZZF10两个测试函数集上的平均运行时间.所有统计结果分别展示在表1与表2中(‘+’与‘−’分别表示每一种算法优(等于)与劣于其他算法).

Table 1 Statistical results of mean IGD and Std obtained by five algorithms on F1～F9 over 30 runs表1 5种算法在F1～F9测试函数上独立运行30次获得的IGD均值与标准差统计结果

Table 2 Statistical results of mean IGD and Std obtained by five algorithms on ZZF1～ZZF10 over 30 runs表2 5种算法在ZZF1～ZZF10测试函数上独立运行30次获得的IGD均值与标准差统计结果

通过深入分析表1和表2，可以发现如下现象.

1) MOEA/D-CS算法在大多数情况下表现出最好的性能.

在F1～F9测试函数集中，MOEA/D-CS算法有5个表现最好；在ZZF1～ZZF10测试函数集中，MOEA/D-CS算法有6个表现最好.然后，在F1～F9与ZZF1～ZZF10测试函数集中，本文进一步比较MOEA/D-CS与其他算法之间的性能差异.

(1) MOEA/D-CS与MOEA/D-CPS算法相比，MOEA/D-CS算法有15个表现最好，说明增加轻量级代理模型提高了获取最优解的概率.MOEA/D-CS利用分类获得的优良解更靠近P+，而P+更靠近PS，所以优良解也靠近PS.由于PS是近似于分段连续的，目标空间也是分段连续的，所以可以通过估计优良解的目标值近似代替优良解的实际目标值.因为优良解是由邻域个体生成的，此时利用相似性度量方法作为轻量级代理模型估计每个优良解最相似邻域个体，然后可以用最近邻域个体的目标值作为优良解的估计目标值.对于所有优良解，只需要利用其近似目标值计算优良解的排序关系，就可以从所有优良解中找出一个最优解.虽然MOEA/D-CPS算法设计的分类器是有效的，然而MOEA/D-CPS算法采用随机选择优良解作为最优解，这种方式不能保证以较高的概率获得最优解.因此，MOEA/D-CS要比MOEA/D-CPS更有效；

(2) MOEA/D-CS与MOEA/D-DE算法相比，MOEA/D-CS算法有13个表现最好.MOEA/D-CS基于MOEA/D框架，说明融合分类与轻量级代理模型的MOEA/D-CS算法，确实提升了MOEA/D的性能；

(3) MOEA/D-CS与MOEA/D-MO算法相比，MOEA/D-CS算法有14个表现最好.因为MOEA/D-MO算法对所有后代候选解均采用实际目标值评价，那么在相同评价次数作为终止条件下，MOEA/D-MO算法的运行代数要远远少于MOEA/D-CS算法.这说明MOEA/D-CS要比MOEA/D-MO算法更有优势，表现也会更好；

(4) MOEA/D-CS与MOEA/D-SIM算法相比，MOEA/D-CS算法有16个表现最好.MOEA/D-CS算法首先采用有监督分类，能够很好地区分优良解与不良解；然后利用轻量级代理模型可以从优良解中找出最优解.而MOEA/D-SIM直接估计每个候选解与最近邻域个体的相似性，如果候选解不是优良解也很可能通过估计目标值被误认为是最优解，这样，MOEA/D-SIM算法的误差就会非常大，所以MOEA/DCS算法的效果也会优于MOEA/D-SIM算法.

从表1与表2还可以看出，本文提出的MOEA/D-CS算法在大多数测试函数上标准差都是最小的，说明MOEA/D-CS算法是非常稳定的.

2) MOEA/D-CS算法花费的时间代价低于MOEA/D-SIM，但是要高于其他算法.

由于MOEA/D-CS算法的性能最好，在权衡精度与时间代价的情况下，MOEA/D-CS算法花费的时间代价是可以接受的.

(1) MOEA/D-DE算法利用DE算子生成1个后代解，然后利用实际目标值评价与更新操作，因此，MOEA/D-DE算法在两个测试函数集上花费的时间代价最小；

(2) MOEA/D-CPS算法首先利用KNN[29]构建分类器并执行分类操作，然后随机选择一个优良解作为后代解，最后利用实际目标值评价后代解并执行更新操作.因此，MOEA/D-CPS算法花费的时间代价要高于MOEA/D-DE算法；

(3) MOEA/D-MO算法利用DE算子生成3个后代候选解，每个候选解均使用实际目标值进行评价.因此，MOEA/D-MO算法花费的时间代价要高于MOEA/D-DE与MOEA/D-CPS算法；

(4) MOEA/D-SIM直接利用余弦相似性估计每个候选解的目标值，这需要花费相当大的时间代价.因此，MOEA/D-SIM花费的时间代价最高；

(5) MOEA/D-CS算法融合分类与轻量级代理模型执行后代个体选择.MOEA/D-CS算法花费的时间代价高于前3种算法，其主要原因有两个:第一，本文利用余弦相似性构建轻量级代理模型，因为每个优良解都需要与邻域个体计算相似度，所以会耗费一定的运行时间；第二，本文使用的测试函数都相对简单，每个子问题产生的后代解数量较少，评价个体目标值花费的运行时间要少于计算相似度花费的运行时间.MOEA/D-CS算法花费的时间代价低于第4种算法，其主要原因是MOEA/D-CS算法采用先分类后估计优良解目标值的方式，相比于MOEA/D-SIM算法采用估计全部候选解目标值的方式，时间代价要小.

为了深入分析不同类型多目标测试函数对算法性能的影响，本文从F1～F9与ZZF1～ZZF10测试函数集中选择了一部分有代表性的测试函数F3，F4，F6，ZZF1，ZZF7和ZZF9.在这些测试函数中，包含MOEA/D-CS算法性能明显优于其他算法的测试函数(F3，F4，ZZF7)，也包含其性能逊于其他算法(F6，ZZF9)或者与其他算法取得相同性能(ZZF1)的测试函数.其中，F3，F4，ZZF1，ZZF7和ZZF9是2目标函数，它们具有相似的PF，而它们的PS形状是不同的非线性曲线.F3和F4具有比其他2目标函数更复杂的PS形状.F6是3目标函数，其PF和PS都最为复杂.图3展示了MOEA/D-CS算法在这些有代表性的测试函数上获得的最终解集.

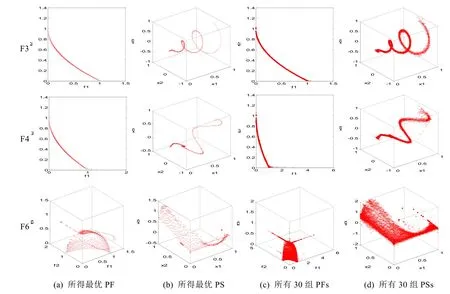
Fig.3 Final obtained approximations by MOEA/D-CS图3 MOEA/D-CS算法获得的最终解集

Fig.3 Final obtained approximations by MOEA/D-CS (Contiuned)图3 MOEA/D-CS算法获得的最终解集(续)

通过深入分析图3，可以发现如下现象.

1) MOEA/D-CS算法非常适合处理PS相对平滑的多目标测试函数.针对F3，F4和ZZF7这3种测试函数，PS与PF都比较平滑，在这几个测试函数上获得的IGD均值为最小值.MOEA/D-CS算法首先利用分类获取优良解；然后，如果条件满足，则利用余弦相似性计算每个优良解与邻域个体的相似程度，此时获得的最近邻域个体是非常接近的，那么对应PF空间的目标值也应该是非常接近的.算法利用近似目标值估计优良解的优劣，很容易从优良解中找出最优解.因为MOEA/D-CS算法融合了分类与代理的混合个体选择机制，所以它提高了获得最优解的概率；

2) MOEA/D-CS算法处理PS非常平滑的多目标测试函数，与其他流行的基于分解多目标进化算法取得了相同的性能.针对ZZF1测试函数，其对应的PS是非常平滑的，此时，无论利用哪一种多目标进化算法，只要评价次数足够多，最终的IGD均值都是相等的；

3) MOEA/D-CS算法处理PS具有复杂曲线形状的多目标测试函数，表现不如其他算法.针对F6与ZZF9测试函数，越是具有复杂曲线形状的多目标测试函数，利用余弦相似性估计每个优良解的目标值所产生的偏差就越大，所以MOEA/D-CS算法不适合处理PS具有复杂曲线形状的多目标测试函数.这也是该算法需要进一步改进的地方.

3.3 收敛性实验

为了验证MOEA/D-CS算法的收敛性，本文从F1～F9与ZZF1～ZZ10测试函数集中选取了F3，F4，ZZF3与ZZF7这4个多目标测试函数，这5种算法利用函数评价次数(FES)作为终止条件获得的平均IGD(log)指标值如图4所示.从图4中可以发现，MOEA/D-CS算法在不同运行阶段收敛性都是最好的.在迭代优化过程中，对应相同的函数评价次数(FES)，MOEA/D-CS算法的平均IGD(log)指标均为最小值，并且MOEA/D-CS算法对应的平均IGD(log)曲线始终呈现递减的趋势，这说明MOEA/D-CS算法取得了比其他算法更好的收敛性.

Fig.4 Mean IGD(log) values versus numbers of FES obtained by five algorithms over 30 runs图4 5种算法利用评价次数作为终止条件独立运行30次获得的平均IGD(log)值

3.4 敏感性参数分析

本文深入分析敏感性参数对MOEA/D-CS算法性能的影响.在MOEA/D-CS算法中，有两个敏感性参数:DE算子中的参数F和种群规模N.

1) 本文分别设置了参数F为单值与组合的形式.如图5(a)和图5(b)所示:在随机选取的测试函数F4和ZZF7上，F以组合形式选取{0.5，0.7}均取得了最好的效果.这样选取参数F可以保证MOEA/D-CS算法具有更好的性能.因此，对于MOEA/D-CS算法来说，选择合适的参数F值是非常重要的；

2) 本文设计了不同种群规模情况下的参数实验，研究不同种群规模对MOEA/D-CS算法性能的影响.这里，设置种群规模N=[50，100，200，300].如图5(c)所示，种群规模对平均IGD(log)指标值产生重要的影响.随着种群规模的不断增加，平均IGD(log)指标值越来越小.因此，PF越来越接近了最优边界PF*.如图5(d)所示:随着种群规模的不断扩大，MOEA/D-CS算法运行时间也不断增加.所以必须同时兼顾算法的精度和时间代价，合理地设置种群规模以满足实际问题的需求.

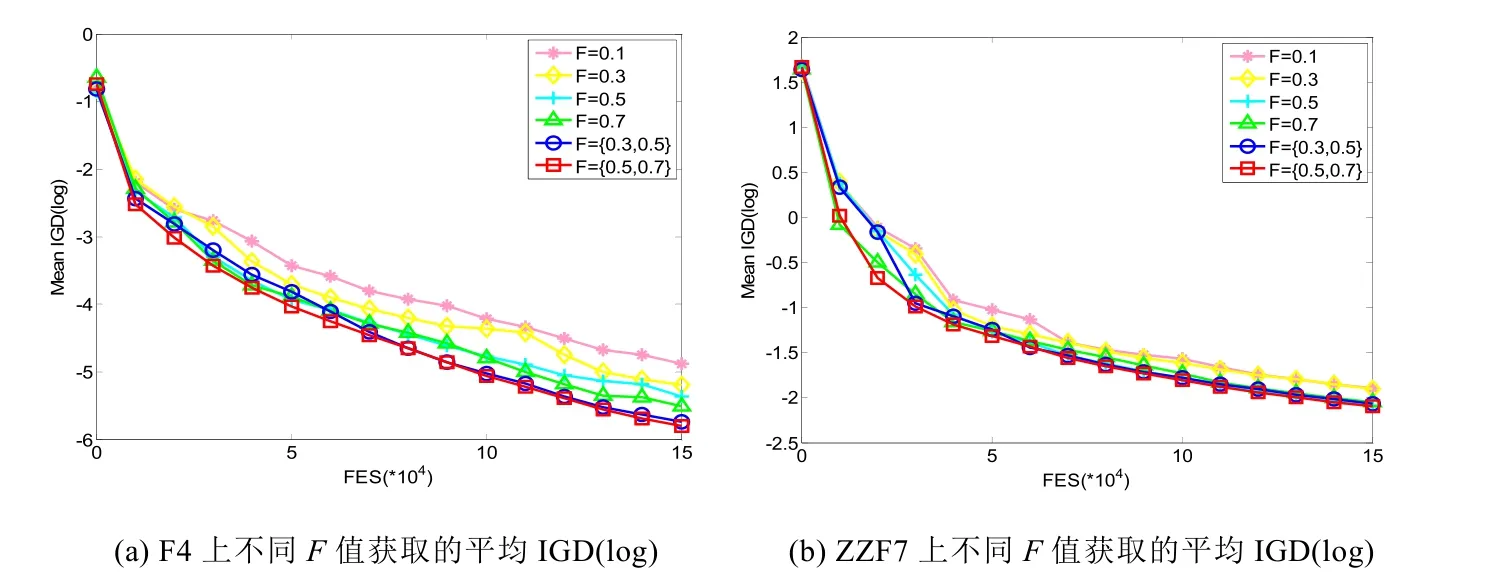
Fig.5 Performances of MOEA/D-CS with setting different parameters图5 设置不同参数情况下MOEA/D-CS的性能

Fig.5 Performances of MOEA/D-CS with setting different parameters (Contiuned)图5 设置不同参数情况下MOEA/D-CS的性能(续)

4 结论

本文提出了一种基于混合个体选择机制的多目标进化算法，融合有监督分类与轻量级代理模型实现后代个体选择.大量实验结果表明:与当前流行的基于分解多目标进化算法相比，在没有显著增加时间代价的情况下，本文所提出的MOEA/D-CS算法能取得较好性能.未来工作包括:(1) 设计适用于处理具有复杂PS曲线形状的多目标进化算法；(2) 将MOEA/D-CS算法应用于实际多目标优化问题.