多步前进同步并行模型∗

张尉东，崔 唱

1(北京大学 信息科学技术学院，北京 100871)2(北京大学 元培学院，北京 100871)

在过去的十几年中，各种用途的处理框架相继被开发出来，如为通用数据处理而开发的Hadoop/Spark/Dryad[1−3]，为蛋白质折叠而开发的GROMACS[4]，为海洋、气象气候科学而开发的CORSIKA[5]以及为材料工程科学、天文天体物理和社会科学开发的NAMD[6]、FLASH[7]和Swarm[8]等.

无论是并行计算框架还是并行算法，并行化都需要一种或多种并行计算模型来指导其实现.常见的并行计算模型包括大同步并行(bulk synchronous parallel，简称BSP)[9]、异步并行(asynchronous iterative algorithm，简称AiA)[10]、时间并行(parallel in time，简称PiT)[11]、logP[12]和轮回并行(samsara parallel，简称SP)[13]等.然而，所有这些并行计算模型都采用无差别的方式来处理稀疏和稠密数据集，这就忽略了数据集内部所蕴涵的独特性(如局部性分布、依赖关系密度等).这不仅导致了大量的无用计算和迭代步，还导致计算时间和收敛结果不受控制.一个经典的例子是使用通用计算机集群(commodity machine cluster)在两个稀疏程度不同但直径相同的图上执行BSP模型并行化的单源最短路算法，其所耗时间几乎相等.原因是它们使用了相同的迭代轮数，而每轮迭代的时间基本都消耗在全局同步上.

为了追求更快的收敛速度，各种应用的异步算法相继被设计出来.异步算法可以在时间上重叠计算和通信，从而实现更灵活地利用数据内部的局部性，达到加速算法收敛的目的.异步算法的缺点也比较明显.除了需要针对单个问题单独设计相应的算法和终止条件外，还会比同步算法耗费更多的通信和计算.SP与BSP和AiA相比，其每次向前投机地计算多步，再将多步计算结果统一打包并交换.在将交换的数据校验后，若发现某步结果不对，则将所有进程跳回最早出错的一步重新计算.尽管SP可能进行更多的无用计算，但每次大同步却可以投机地前进多步，且每步都能和BSP的迭代步一一对应.

就我们所知，目前还没有一个模型可以在不修改算法的前提下，以不同的方式处理稀疏程度不同的数据集.要进行有区别的处理，首先需要挖掘数据中存在依赖关系和局部性分布，即使先不讨论依赖关系和局部性，如何构造出根据不同的数据集产生不同并行行为的并行程序也缺乏相应的理论指导.在日常数据处理工作中，我们发现大量并行算法仅在满足弱一致性条件时即可收敛；同时，大多数数据都是相当稀疏的.结合这两方面，我们认为可以通过进一步挖掘和利用数据分区中的局部性，首先加速局部收敛进而促进全局的收敛.

通过数学建模和形式化推导，我们发现本文提出的多步前进同步并行(delta-stepping synchronous parallel，简称DSP)模型是一种比BSP更一般的同步并行模型.它可以更充分地挖掘和利用隐藏在数据中的局部性来加速算法的收敛.进一步的实验同样验证了这个结论.DSP与BSP唯一的不同点在于:在每个超级计算步内，DSP执行Δ步局部计算(Δ≥1)；而BSP仅执行1步局部计算.引入更多局部计算的目的在于进一步挖掘和利用蕴含在数据分区内的局部性，进而加速局部收敛、减少迭代轮数和通信开销.在通用计算集群中，对于计算量少但迭代步数多的算法，迭代轮数的减少直接意味着收敛时间的减少.原因是这种类型的算法将大部分执行时间都消耗在全局同步上.在表1中，我们将DSP与几种常见的并行计算模型进行了比较:(i) 同步方式——同步、异步；(ii)迭代次数；(iii) 与BSP每步结果是否能对应上，结果是否收敛.

Table 1 Comparison between common parallel models and DSP表1 常见的并行计算模型和DSP的比较

本文有如下贡献.

1) DSP并行计算模型:本文提出了一种新的并行计算模型，可用于加速一大类并行迭代算法.

2) 并行计算模型的形式化表示方法:本文提出了一种形式化表示方法，可以很好地表示各种并行计算模型及其迭代过程.

3) 正确性和适用性证明:利用贡献2)中给出的形式化方法，推导并证明了DSP的适用性及收敛条件.

4) 编程指导:为指导用户将BSP程序改写或直接构造DSP程序，给出了具体的实施步骤.

本文首先介绍若干相关工作，包括BSP、参数服务器等模型.为了对DSP建立一个初步映像，第2节列举DSP的几个应用场景.第3节描述并行模型的形式化表示方法，并使用该种方法表示BSP和DSP的迭代过程，推导和证明BSP和DSP的等价收敛条件.第4节使用真实数据集和实际应用验证并评估DSP模型的加速性能.第5节是总结和工作展望.

1 相关工作

1.1 大同步并行模型(BSP)

Leslie Valiant于1990年在牛津大学提出了著名的BSP并行计算模型.该模型主要用于指导同步并行算法或程序的设计.一个典型的 BSP算法或程序由如下 3部分组成:局部计算(local computation)；通信(communication)；阻塞同步(barrier synchronization).

BSP算法的一个超级计算步(superstep)可以描述为图1所示的过程.

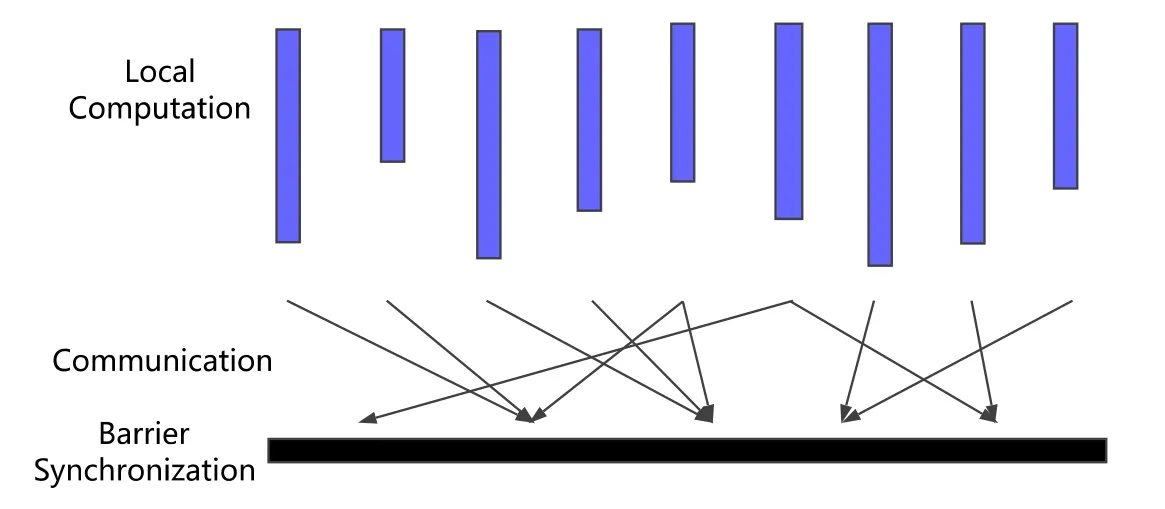
Fig.1 BSP pattern[14]图1 BSP算法执行流程[14]

与BSP相比，DSP简单地将单步局部计算变为Δ步局部计算(Δ≥1)，新增加的局部计算步只是简单地重复执行之前的计算.DSP算法的一个超级计算步可以描述为图2所示的过程(DSP将局部计算步数变为Δ步.局部计算时，只更新本地变量，不进行节点间通信).同时，我们将额外增加的(Δ≥1)步局部计算称为投机计算步(speculative computation step，简称SCStep)，其定义如下.

投机计算步(SCStep).BSP局部计算的简单重复，期间只做局部数据更新，计算节点间无数据通信发生.

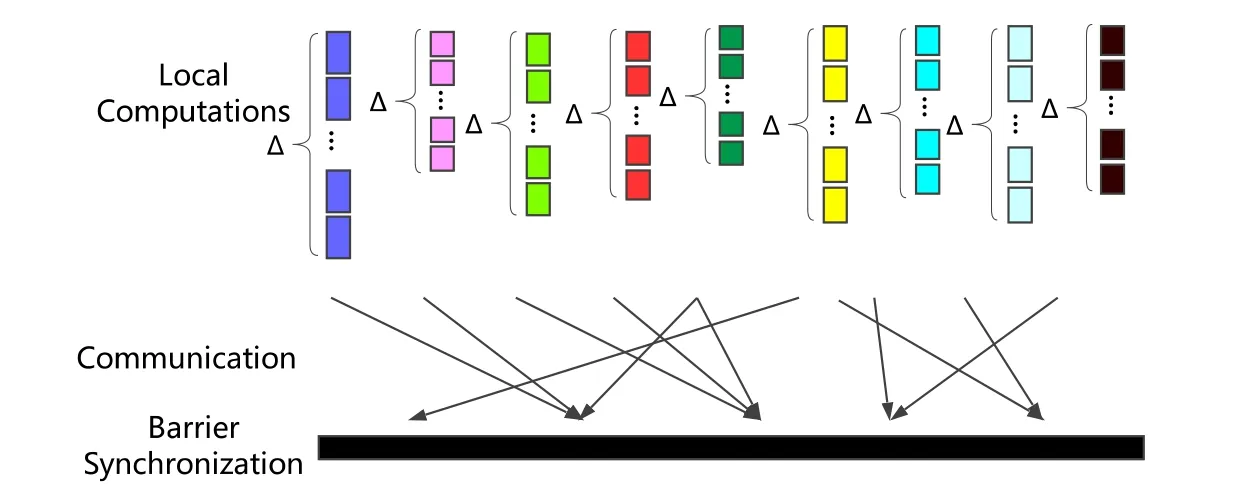
Fig.2 DSP executing pattern图2 DSP算法执行模型

1.2 参数服务器

为了解决大规模分布式机器学习中数以百万计参数频繁更新的问题，Google在2012年提出了参数服务器的方案[15].参数服务器允许各个模型副本在一个很小的时间间隔内，异步地更新和下载中心参数服务器中最新的参数.这样一来，各个模型副本就可以减少使用参数服务器时互斥等待的时间.虽然在允许的时间间隔内，各个模型副本从参数服务器上获取的数据并不一致，但算法最后却能收敛.Google的论文[15]中展现了参数服务器惊人的加速潜能，同时也表达了对加速原理的疑惑.进一步工作[15−19]分别将参数服务器用于加速不同的应用，并分别给出了收敛性证明.然而到目前为止，还没有一个正确性的一般性证明.与参数服务器不同的是，DSP算法除了支持一大类机器学习的优化算法以外，从根本上是针对并行迭代计算提出的，因而几乎可以适用于所有的并行迭代计算.针对其适用性和正确性，本文给出了一个一般性证明及适用约束条件.

另外，参数服务器的相关工作并没有解释其加速原理，本文中对DSP加速原理的解释同样适用于解释参数服务器加速的原理.

1.3 其他工作

(1) KLA:K层异步算法(K-level asynchronous，简称KLA)[20].DSP与KLA的不同主要体现在以下几点.

· DSP仅仅在大同步时才进行节点间通信，而KLA在局部计算时也会进行节点间通信.因而，DSP比KLA更简洁，同时也具备比KLA更好的扩展性和更广的适用范围.实验中我们发现，通信的开销不仅仅与通信的次数相关，而且还受到消息长度的极大影响.

· DSP的应用不限于KLA所局限的图计算领域.

· DSP不是KLA的特例，KLA也不是DSP的特例.

(2) 多步并行最短路算法(Δ-stepping:A parallelizable shortest path algorithm)[21，22]:通过维护一个待选顶点的列表，每次向前尝试性地进行Δ步迭代.DSP并不需要显示地维护这样一个列表和待选数据集，只需在数据分区中简单重复地执行相同的操作并更新局部数据，就可以达到与该算法相同的效果.DSP用于加速单源最短路算法的示意图如图3所示.虚线界定的网格代表一个计算节点，每个计算节点负责计算图中部分顶点的最短路.由于DSP每个超级计算步可以执行Δ次局部计算和局部更新，而BSP却只能执行1次，所以着相同颜色的顶点可以在同一轮大同步求得最短路.求得图3(a)中所有顶点的最短路仅需5轮全局大同步，求得图3(b)中所有顶点的最短路则需要13轮全局大同步.

Fig.3 Solving procedures of single source shortest path (SSSP) from all other vertices to vertex S with DSP and BSP model respectively图3 分别使用DSP和BSP模型求解图中所有顶点到S 点的单源最短路

2 应用举例

正式描述模型之前，为对DSP建立一个初步的映像，首先介绍几个简单的例子.

· 图并行算法

将DSP用于加速图并行算法时，可以很好地解释DSP的工作流程及原理.如图3所示，将DSP用于加速单源最短路(SSSP)算法，图中每个虚线界定的网格表示一个计算节点，每个计算节点负责图中一部分图顶点最短路的计算.BSP模式下，每个超级计算步每次计算仅向前推进1步，而DSP每次却可以前进多步，甚至将最短路在一个超级计算步就传递给相邻的下一个网格.对其他图算法如PageRank等，多步局部计算同样可以通过更充分利用数据分区内的局部性加速子图内的局部收敛，进而促进算法的全局收敛.

· 求解线性方程组

在某些工程和科研应用中，部分线性方程组的系数矩阵如此稀疏，以致于可以将未知数向量X分为多段，分别进行独立求解.并行求解这类型方程组实际上只需很少的通信，即可达到较高精度的收敛.因此，DSP模型十分适合用于加速稀疏线性方程组的求解.

· 机器学习

机器学习的训练数据通常由数10亿级的高维向量组成，同时，学习模型的参数也由数百甚至上千维的向量组成.然而，由于数据和模型的稀疏特性，分布于不同计算节点上的参数之间的严格同步并非必备条件，甚至部分节点的数据之间并不存在相互依赖，因此，分布式优化算法十分适合采用DSP进行加速.

3 模型及其收敛性保证

DSP模型的目标是在不影响算法收敛的前提下，通过减少算法的迭代轮数来减少算法在通信上的开销，进而加速算法的收敛.为了实现这个目标，我们发现，不同于稠密数据集上的迭代计算，稀疏数据集上的迭代计算拥有更小的计算通信比:Tcomputation/Tcommunication，即迭代时间主要耗费在通信上，而非计算.因此，通信开销的减少可以有效地加速并行算法的收敛.此外我们还发现，仅仅1步局部计算很难充分挖掘和利用数据分区内的局部性.对于一大类图并行算法，1次局部计算对应着1次局部值传递，那么多步局部计算意味着多步局部值传递.然而，投机计算步并非越多越好，因为投机计算步是以增加计算量为代价，当集群节点间初始负载不均时，太多的投机计算步甚至会加剧这种不均衡.

分析表明，投机计算步具备如下两个特征:(i) 尝试在数据分区内通过更充分地挖掘和利用空间局部性，实现空间局部性最优；(ii) 尝试在一个超级计算步内通过更多的执行投机计算步实现超级计算步内的时间局部性最优.简而言之，DSP通过执行合理数量的投机计算步实现空间和时间上的局部最优.如果这里的空间和时间局部最优正好发生在某些适合的算法或作用于稀疏数据集上，那么它极有可能转化为最终和全局的最优.

此外，DSP还具备一些其他优点.如:(i) 当应用于值传递算法时，可同时适用于稠密和稀疏数据集；(ii) 当用于加速雅各比迭代时，展现出了类似于超松弛(successive over-relaxation，简称SOR)[21]的加速效果，即同时减少了局部计算步和全局同步轮数.

3.1 形式化表示

为了统一表示和比较不同的并行计算模型，本文提出了一种类似于“矩阵乘法”的转换:Xk+1=Xk⊗Fn×m，其中，Xk，Xk+1分别为第k轮迭代的输入和输出变量，Fn×m为迭代计算进行的操作.不同于代数中的矩阵乘法，Fn×m中的每个元素Fi，j表示输入向量Xk的分量xi与xj之间进行的计算，其结果返回给xj.得到xj所有依赖的分量与xj运算后的结果，再将这些结果进行聚合，聚合的结果将作为xj本轮计算的输出.直观上理解，xj下一轮的新值实质上是将它依赖的每个分量对它产生的影响或改变进行聚合的结果.类似的表示方法也在文献[23，24]中出现，不同的是，我们进一步推导出了输入变量X随迭代进行的演变形式.

为使下文更简洁地表达和推导，首先定义如下变量和符号.

1)X0:迭代计算的初始输入变量.

其向量表示为(x0，x1，...，xn).xi可以表示各种类型的数据，如图计算中顶点信息、线性方程组中的未知数等.

2)Xk:迭代计算的第k轮输出.

并行化时，变量Xk被切分为多段并分布在不同的计算节点上进行计算，X(p，q)k表示某个计算节点仅负责计算从xp到xq一段的分量.

3)F:关系矩阵.

Fi，j定义xi与xj之间的运算，函数形式为Fi，j(xi，xj)，简写为Fi，j(xi).其运算结果返回给xj供其进一步与其他所依赖的变量计算产生的结果进行聚合(具体实现时，Fi，j通常被表达为一个数学公式、函数、过程或方法).

F(p，q)表示对输入变量进行一次部分转换.F(p，q)仅计算和更新xp到xq之间的变量.其定义如下.

使用向量与矩阵相乘的规则，X的分量被投射到Fi，j上进行运算，最终只有xp到xq之间的变量进行了运算和更新，其余分量保持不变.

此运算符将{Fi，j(xi)|i=0，1，2，...，n}中所有运算结果进行聚合，聚合得到的值将作为xj本轮迭代计算的输出.公式为

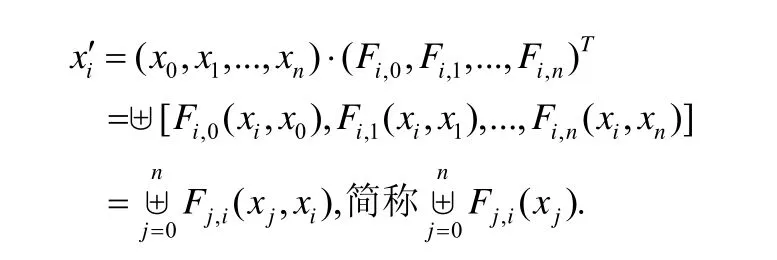
常见的聚合操作有min(⋅)，max(⋅)，average(⋅)，Σ，Π等.

5) ⊗:转换运算符.

该运算符将关系矩阵在输入变量上作用1次.

表2中列举了几种常见算法的关系函数和聚合函数.

Table 2 Common algoriths and corresponding relation/aggregation functions表2 常见算法及其对应的关系函数和聚合函数

使用如上定义的变量和符号，BSP模型的迭代过程可推导如下.

通过如上推导，我们发现，k轮BSP迭代可由k次关系矩阵的转换来表示.

类似地，对X0进行l轮DSP迭代，可得到对应的XlΔ(每轮DSP大同步对应进行Δ步局部计算，详细推导过程见https://github.com/wdfnst/DSP_Proof/blob/master/dsp_proof.pdf):

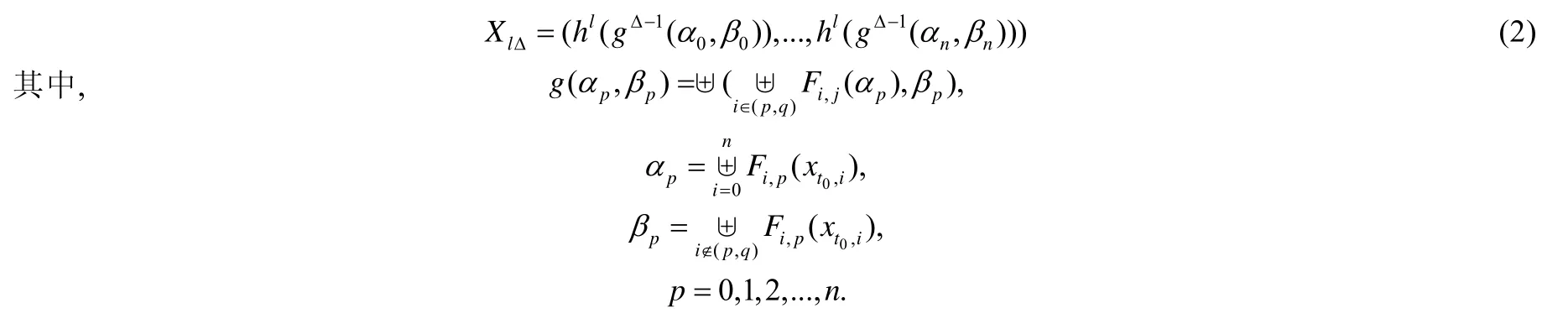
直观上理解，公式(2)中的参数解释如下.

·g(αp，βp):将BSP中一次局部计算变为两次局部计算后产生的新算法.

·αp:聚合xp所有依赖的变量对其作用的结果.

·βp:聚合xp所依赖的且位于不同计算节点上的变量对其作用的结果.βp也可视为xp对其他分区数据的依赖程度.

·γp(=αp−βp):聚合xp所依赖的且位于相同计算节点上的变量对其作用的结果.γp也可视为xp对分区内数据的依赖程度.

要使用DSP加速BSP，即在迭代中用公式(2)表示的计算替换公式(1)表示的计算，首先需要证明它们可以收敛到相同的最终状态.然而公式(2)并不能保证收敛到与公式(1)相同的最终状态.但对于凸优化问题或只要求收敛到局部最优点的算法，达到收敛就足够了.第3.2节将使用数学归纳法证明DSP的收敛条件.

3.2 DSP模型的收敛性保证

包括参数服务器和DSP模型在内的许多模型或算法[22−25]都使用了投机计算的思想，然而，其中仅部分模型或算法给出了正确性解释或适用条件说明.在没有正确性保证的前提下，用户在选用这些方法时始终保持着谨慎的态度.本节将给出BSP和DSP的关系，并推导出DSP的收敛条件.

定理1.如果算法在BSP模式下收敛，那么，当且仅当满足如下条件时，算法在DSP模式下也收敛:

直观上理解，定理1描述了在BSP模式下收敛的算法，若增加一次局部计算后得到的新算法仍然收敛，那么增加任意数量的局部计算得到的新算法都将收敛.

证明:当Δ=1时，DSP模型退化为BSP模型.故Δ=1时，结论成立.假设当Δ=k(k≥1)时，结论仍然成立，即

收敛.

那么当Δ=k+1时，得到如下左式，并变形为右式:

对比公式(4)、公式(5)，在BSP模式下，因为αp收敛，所以公式(4)收敛.从而，公式(5)收敛的条件是:

在满足条件(6)时，定理1对Δ=k+1成立.

由数学归纳法原理可知:在满足条件(6)时，定理1对所有Δ∈Ν+成立.□

3.3 DSP加速因素分析

由公式gΔ˜1(αp，βp)可知，DSP算法的收敛速度主要依赖于3个因素:Δ，αp和βp(其中，p=0，1，2，…，n)，并存在如下关系.

· 当βp=0时(可理解为xp的收敛不依赖任何位于其他计算节点上的变量)，xp在不需要任何全局数据同步的前提下即可收敛.这时，额外的(Δ−1)步投机计算可以获得非常显著的加速，以至于当Δ充分大时，xp可以在不需要任何全局同步的情况下直接收敛.图4(a)示例了这种情况，每个数据分区被分配到不同的计算节点，彼此之间不存在任何依赖关系，这个图上的并行迭代计算可以在不需要任何全局数据同步的情况下收敛.

· 当γp=0时(可理解为xp的收敛完全依赖于位于其他节点上的变量)，因为xp所依赖的变量在Δ步局部计算中并不会更新，所以Δ次局部计算产生的新值也不会有任何变化.图4(c)示例了这种情况，图中每个分区中的顶点所依赖的变量全部位于其他计算节点内，这种情况下，额外的(Δ−1)次局部计算不会产生任何加速效果.

· 当γp＞0时(即xp所依赖的变量部分位于和自己相同的节点内)，额外的(Δ−1)步计算会促进xp更快地收敛，且加速效果与γp成正比.

· 当βp＞0时(即xp所依赖的变量部分位于其他节点)，第1次局部计算之后，βp并没有及时从其他节点获取最新值进行更新，剩下的(Δ−1)步局部计算仍然使用上次全局同步的变量计算产生的βp.过期的βp对xp的收敛其起副作用，DSP的加速效果与βp成反比.图4(b)示例了这种情况，每个分区内的顶点所依赖的变量既有来自本节点的，也有来自其他节点上的.

某种意义上，γp和βp可分别用数据分区内和数据分区间的依赖关系密度来解释.若能通过适当的数据划分增加分区内依赖关系密度(即增大γp)，同时减小分区间依赖关系密度(即减小βp)，那么算法的收敛极有可能得到加速.然而，完美的数据切分(如图划分)通常都是NP难问题.尽管增大γp比较困难，足够小的βp却十分普遍.因为稀疏数据集划分之后得到的βp通常都会非常小，这就为我们使用DSP加速迭代计算创造了条件.

为了验证βp，γp与加速效果之间的关系，我们使用PageRank算法在随机图上进行了两组实验:(i) 固定子图内的连接度，变化子图之间的连接度；(ii) 固定子图间的连接度，变化子图内部的连接度.实验结果如图5所示，图5(a)显示，加速比#Iterationbsp/#Iterationdsp随着增加的β而下降，即子图间连接增加后，DSP的加速性能下降了.图5(b)显示，加速比#Iterationbsp/#Iterationdsp随着增加的γ而上升，即子图内连接增加后，DSP的加速性能上升了.这一结果进一步验证了我们上面的分析.

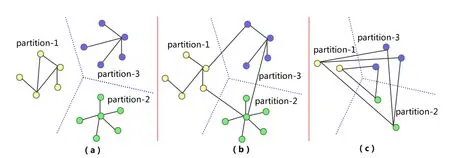
Fig.4 图4

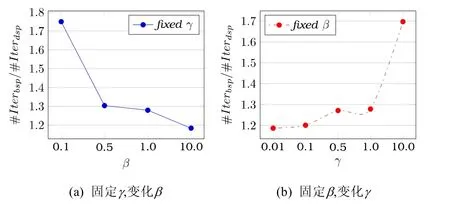
Fig.5 Acceleration of DSP on PageRank图5 DSP对PageRank的加速

3.4 DSP并行算法的构造

对比算法1、算法2，将BSP算法改造为DSP算法或直接构造DSP算法只需在进行全局通信前增加一个条件测试(测试是否执行了指定步数的局部计算).构造DSP程序时，可按如下几步进行.

1) 若BSP算法收敛，则检验拥有两步局部计算的新算法是否收敛，若收敛则转至第2)步.

2) 筛选合适的参数Δ.

3) 调整代码.增加条件测试，使得每执行1次DataExchange(⋅)对应执行Δ次Computing(⋅).

算法1.BSP并行算法模板.

算法2.DSP并行算法模板.

对于各种算法，并没有普遍适用的Δ值.根据第3.3节中的分析可知:当数据集比较稀疏或采用较好的数据划分算法时，可以选用适当大的Δ；反之，适当小的Δ加速效果可能更好.除此之外，非线性是导致变量变化快慢的主要因素之一.当算法非线性较强时，重用剧烈变化的变量值会引入较大的误差，致使收敛速度减慢.所以，非线性强的算法适合选用较小的Δ，反之适于选用较大的Δ.

4 实验与评估

实验中用到的设备主要包括20台高性能服务器及连接它们的高速以太网(40GB/s或换算为3.2GB/s)和InfiniBand网络(6.8GB/s).每台服务器由两片Intel Xeon E5520处理器(4核×2.27GHz)和48G内存以及其他外设组成.除GMRES和SGD外，其他算法都采用C++和MPI通信接口实现.默认情况下，MPI优先使用InfiniBand进行通信，所以这里实现的算法实际上都优先使用InfiniBand进行通信.因为DSP加速的原理是通过减少迭代轮进而减少通信开销实现的，而在高速网络中，由于通信延迟低，DSP的加速性能并没有得到充分的展示.在由TCP/IP网络连接的通用计算集群中，DSP的加速性能会比下面列出的结果更加卓越.

4.1 图算法应用

1) PageRank.PageRank算法通过赋予web网络中每个页面一个权重，并以此来衡量每个页面的相对重要程度.其计算既可通过代数方法求解也可通过迭代法求解，迭代公式为

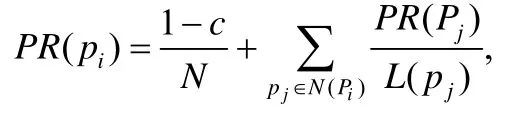
其中，p1，p2，...，pn表示需要计算PageRank值的网页，N(pi)表示所有连接指向pi的网页集合，L(pj)表示网页pj的出度，N表示所有网页的数目.常数(1−c)/N表示网页浏览者随机打开一个网页的概率，这个机制用来解决和防止终止点问题和陷阱问题.

我们收集了3份真实Web图数据，并对其基本信息进行了统计.如表3所示，指标包括顶点数、边数、平均出度、最大出度和最小出度.从其平均出度来看，这些Web图并不稀疏.并且Web图的入度分布一般都高度畸形，即其顶点的入度悬殊非常大.

Table 3 Statistics of real world Web graphs表3 真实Web图及其基本统计信息

将表3中的Web图按顶点近似等分划分，并分发到不同的计算节点.在每个计算节点上每执行Δ步局部计算再进行一次全局大同步.图5(a)～图5(c)展示了DSP的加速效果.数字显示，DSP可以显著减少BSP的迭代轮数，进而减少算法的收敛时间.在这组实验中，我们采用了Metis工具包[26]进行图划分(Metis工具包中实现的算法可以在保证子图间顶点数量均衡的前提下，最大限度地减少子图间割边的数量，从而降低子图间的依赖性；而随机图划分算法仅能保证子图间顶点数量的均衡，不能减少子图间割边的数量，也不能降低子图间依赖的程度).与此同时，我们还在随机划分的子图上进行了相同的测试，结果显示:除Δ=2有少许加速外，DSP算法的收敛速度甚至还不如BSP.这个结果也验证了我们在第3.3节中的分析，即DSP的加速效果十分依赖于β和γ.

图6使用真实Web图和路图，测试DSP对PageRank和SSSP算法的加速性能.图6(a)～图6(c)展示在使用Metis工具包切分的子图上，DSP对PageRank加速性能；图6(d)～图6(f)展示在使用Metis工具包切分的子图上，DSP对SSSP的加速性能；图6(h)～图6(g)展示在使用随机划分的子图上，DSP对SSSP的加速性能.PageRank算法的收敛精度设为10−10.

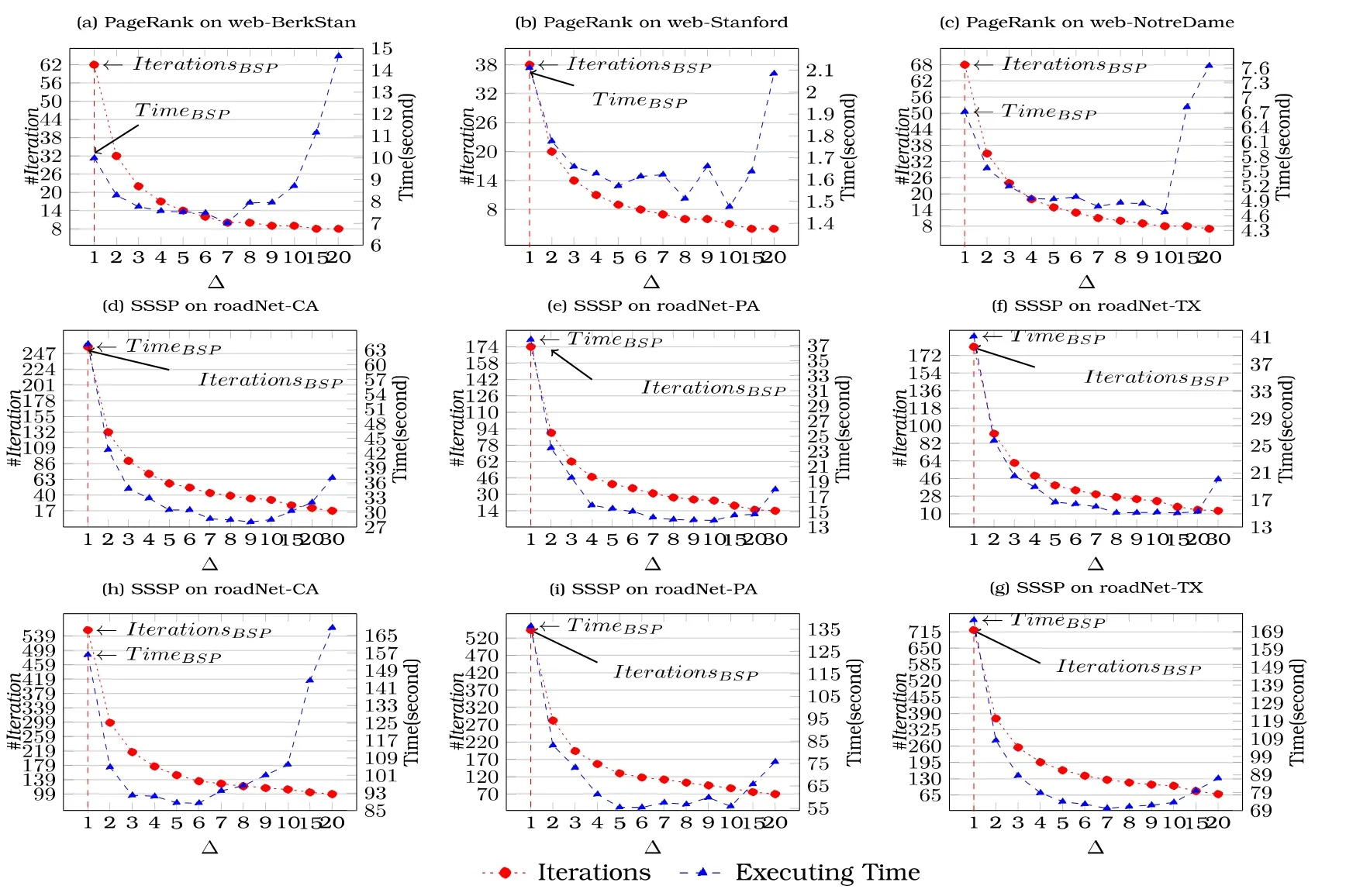
Fig.6 Performance comparison between DSP and BSP working on PageRank and SSSP with the real Web graph图6 使用真实Web图和路图，测试DSP对PageRank和SSSP算法的加速性能

2) SSSP.给定一个有向赋权图G(V，E)，SSSP算法用来寻找图中所有点到指定源点的最短距离.

为了方便说明，图3中示例了一个简单的单源最短路求解的例子，以说明DSP加速单源最短路这类图算法的原理.图中每个虚线界定的网格表示一个计算节点，分别负责计算图中部分顶点的最短路.图3(a)、图3(b)中随着着色的变化(或加深)，分别展示了DSP和BSP迭代的过程.由于DSP在一个超级计算步中可执行多次局部计算，从而可以将最短路向前传递多步，而BSP每次只能前进1步.图3(a)中使用DSP加速，整个计算过程仅需5次全局大同步即可收敛，而图3(b)使用BSP迭代，则需要13次大同步.在这个例子中，DSP的加速比为2.6倍.

为了验证DSP在实际路图中的加速性能，采用美国若干州的路图进行了实验.同样，为了验证第3.3节中的分析，如下两种图划方法被用于图划分:(i) 随机划分；(ii) Metis划分.路图的的基本信息及统计信息见表4，可以看出，路图是比Web图稀疏得多的自然图.

Table 4 Statistics of real world road networks表4 真实路图及统计信息信息

如图6所示，图6(d)～图6(f)、图6(g)～图6(i)分别展示了在采用不同图划分方法得到的子图上进行实验的结果.数字显示，算法在Metis划分的子图上的性能是在随机划分的子图上的性能的数倍.这一结果进一步验证了我们在第3.3节中的分析.同时，仅采用随机分图，DSP对BSP的加速也可高达10倍.

4.2 线性方程组求解

设AX=b表示一个由n个线性方程组成的线性方程组，其中，

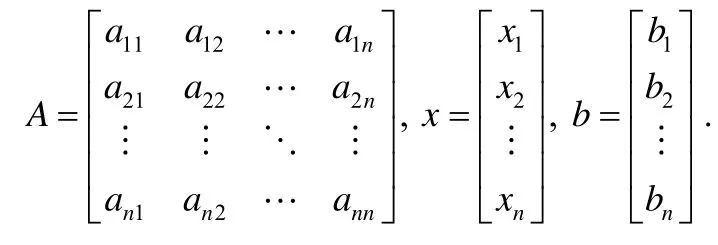
当系数矩阵A为低阶非稠密矩阵时，使用高斯主元消元法可以进行非常高效的求解.但当系数矩阵为稀疏矩阵时，迭代法则更加高效，它能更充分地利用系数矩阵中出现的大量零元，进而避免大量不必要的计算.Jacobi迭代法求线性方程组的迭代公式为

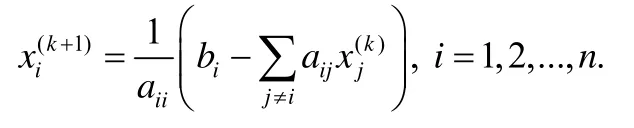
超松弛法(successive over-relaxation，简称SOR)[21]是Jacobi迭代法的一种改进算法，可以实现比Jacobi迭代更快的收敛.其迭代公式为

其中，常数ω＞1称为松弛因子.

为了比较DSP和SOR加速Jacobi迭代的原理，我们将执行一步局部计算对xl所做的操作进行如下表示和变形:首先，使用分别表示xi和xl在第(k+1)步局部计算时得到的最新值.

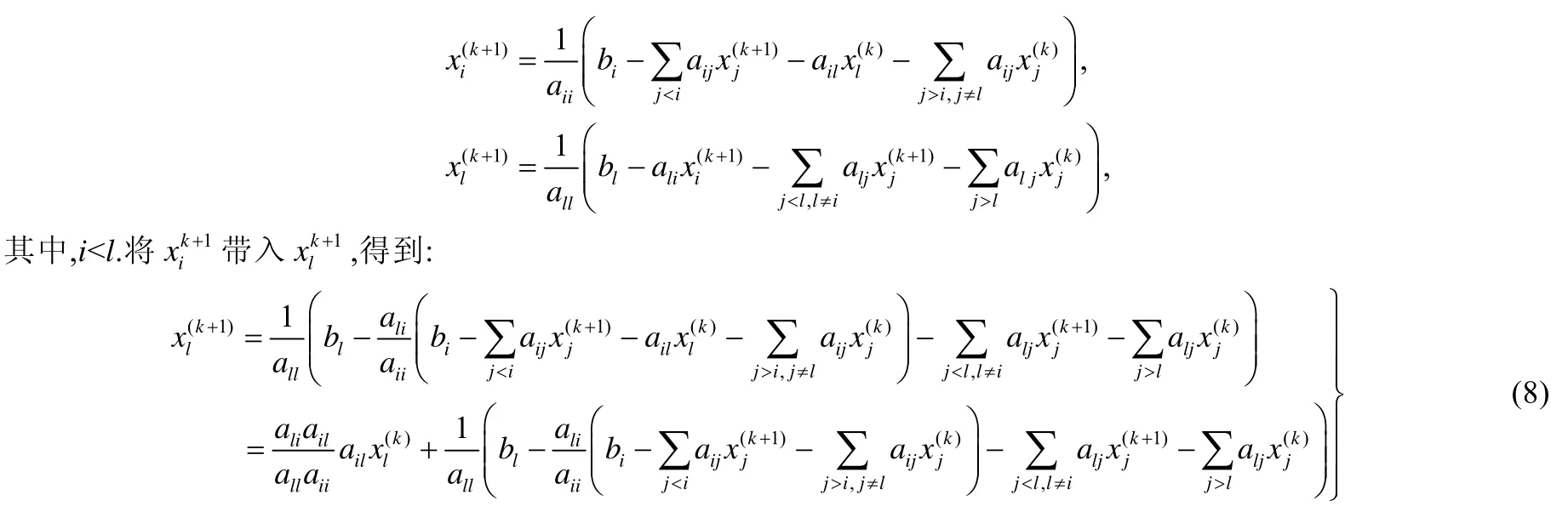
比较公式(7)和公式(8)不难发现，DSP的迭代递推公式和SOR的递推公式有着类似的形式，这进一步验证了实验中的发现，即DSP和SOR可以同时减少计算量和通信量.

实验采用了由10 000个线性方程组成的线性方程组.将未知数向量X等分为20份，并分发到不同的服务器中.每台服务器每进行Δ步局部计算，对应进行一次全局大同步.实验结果如图7所示(收敛精度设为10−14):迭代的步数首先随着Δ的增加而减少，随后稳定在一个值周围.收敛时间随着Δ的增加，先减少再增加.收敛时间下降后再增加是因为投机计算步并非越多越好，它同时也会增加计算负担，进而抵消减少通信带来的好处.

广义最小残差算法(generalized minimal residual method，简称GMRES)[27]是一种被广泛应用的线性方程组迭代求解算法，为了评估DSP的加速性能和扩展性，我们将其与GMRES算法的速度进行了比较.在求解一个由10 000个线性方程组成的线性方程组时，GMRES耗时0.0373 18s和71轮迭代.DSP的性能如图8所示(收敛精度设为10−14)，当Δ=100时，DSP仅耗时0.0187 14s和2轮迭代就达到了和GMRES同样的收敛精度.这一结果显示，DSP在加速Jacobi迭代法时具有比肩最好算法的性能.

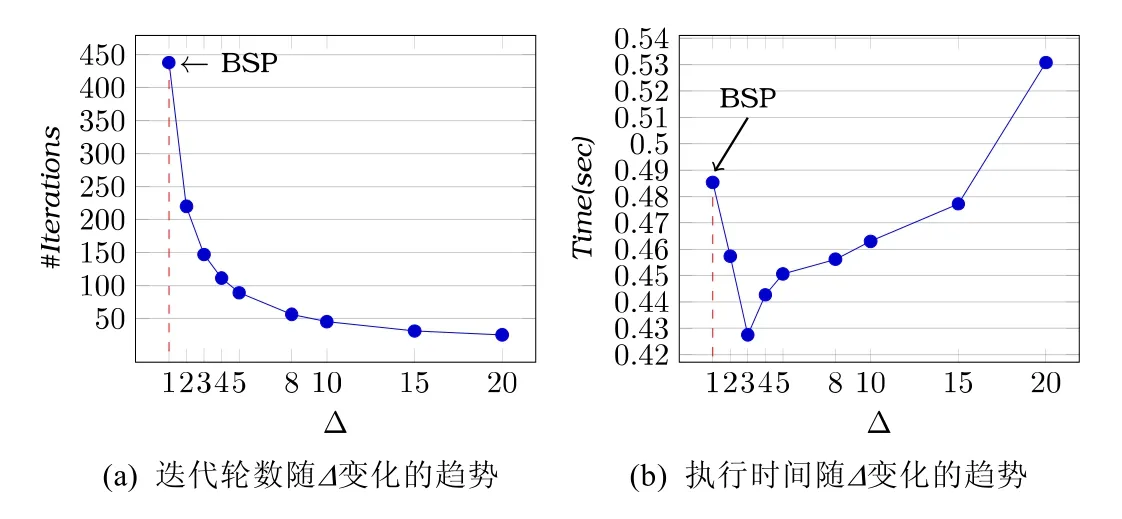
Fig.7 Acceleration of DSP working on Jacobi iterative method图7 DSP对 Jacobi迭代算法的加速性能

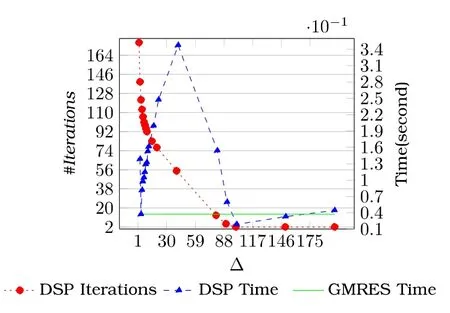
Fig.8 Performance comparison between DSP and GMRES图8 DSP与GMRES性能的比较

4.3 加速分布式优化算法

随机梯度下降(stochastic gradient descent，简称SGD)[28]是梯度下降优化算法的一种近似算法.它通过迭代来求解目标函数的最大或最小值.大量经典机器学习算法的训练过程都可以用 SGD来进行优化，如Perceptron[29]、Adaline[30]、k-Means[31]和SVM[32].

为了验证DSP模型对SGD算法的加速性能，我们进行了一组简单的验证实验.通过分布式的SGD算法来训练一个简单的线性分类器.样本集合由维度为100的稀疏向量组成，所有的样本点被标记为4类，其类别为非零元的位置模4运算的结果所决定.

实验结果如图9所示(全局同步轮数的对数先随Δ的增加呈指数下降趋势，随后稳定在一个数字周围)，全局同步轮数的对数首先随着增加的Δ呈指数级下降趋势，随后稳定在一个值的周围.

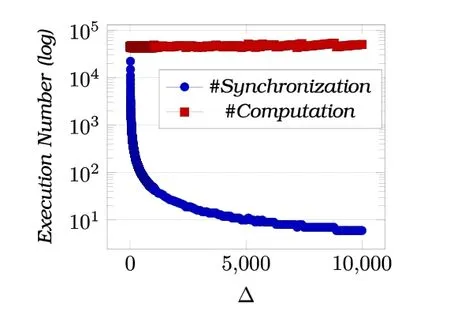
Fig.9 Performance of DSP working on SGD图9 DSP对SGD的加速性能

当Δ足够大时，我们发现参数的收敛仅仅需要数轮同步就可以完成.也就是说，在参数收敛的过程中，大部分数据同步都是不必要的.分析其原因，我们认为模型的参数之间的关系也是相对稀疏的，这才导致所有参数之间并不需要严格的一致也能使模型收敛.

5 总结和工作展望

本文提出了一种并行计算模型，它可以显著地减少迭代计算的轮数.对于瓶颈为通信的算法，迭代轮数的减少直接意味着通信开销的减少，算法的收敛速度也能因此得到相应的提升.除此之外，本文还提出了一种迭代算法的形式化表示方法.使用这种方法，我们表示了BSP和DSP并行计算模型及其迭代过程，发现DSP是一种比BSP更一般的计算模型.在此基础之上，本文进一步给出了DSP的适用条件和收敛性证明.

为了保证第3.1节中推导和证明的一般性，其中出现的符号可用于表示任意关系函数和聚合函数.我们没有提供具体函数的收敛性证明，但通过数值分析的不动点迭代或级数的收敛推导，都可以得到与第3节中相同的结论.通过形式化的表示和推导，我们发现，DSP中增加的局部计算步可以更充分地挖掘和利用数据分区内部的局部性，加速局部收敛，进而促进全局收敛.

实验评估部分展示了若干有趣的发现，比如，加速Jacobi迭代时，DSP模型的执行过程实际上模拟了超松弛的计算；分布式SGD的计算过程实际上只需少量的同步即可实现收敛.在通用计算集群上，DSP可以贡献更好的性能，原因是通用计算集群的通信延迟通常会大得多.

因为DSP加速的原理是“计算换通信”，所以过多的局部计算不仅会增加节点的计算负担，而且当迭代计算的初始负载不均衡时，负载不均衡也可能被加剧.