制胜中考,解决压轴数学题
2019-10-25安徽省临泉县第三中学张俊峰
安徽省临泉县第三中学 张俊峰
对于中考而言,一分之差就能造成天壤之别,很多学生可能就会因为一分而与心仪的高中失之交臂,因而在实际教学中,我们不能以满足的眼光看待学生的数学发展,而是应该学会运用合适的方法帮助学生取得更满意的数学成绩,基于此,在九年级阶段,我们除了要继续强化学生的数学基础知识以外,还要将目光适当放在压轴题上。
一、压轴题的数学教学方法
1.缓解学生畏难心理
中考数学压轴题一般分为三个小问题,在实际教学中,我们就可以运用压轴题模拟训练的方法,通过分层教学的方式,对不同学生提出不同要求,以此为学生数学的进一步发展奠定基础。如我们可以要求低层次的学生将目光放在第一问上,中考数学压轴题的第一小问一般就是对已知条件的分析,这一问实际上并不困难,所以我们就可以要求低层次的学生尽量完成第一个小问题;对中间层次的学生,我们可以让其在解决完第一个问题以后,尝试解决第二个小问题,中考数学压轴题的第二小问一般是在分析完已知条件以后,运用相关数学思想就能解决的问题,在这种问题的解答中,只要我们平常多加训练,那么其难度也并不会很大;在中考数学压轴题的解题中,难就难在第三个小问题,在这个问题的解答中,我们可以要求学生再读题目并对已知条件进行更深度的分析,然后结合自己所学知识及第一、第二问的答案考虑题目的解决思路。要想制胜中考压轴题,我们就必须先努力缓解学生的数学畏难心理。
2.教会学生解题技巧
当我们将压轴题掰开揉碎了分析完以后,学生在心理上就能更好地接受这种题目,但是光是心理接受没有知识基础也是不够的,因而在实际教学中,我们还应该适当教给学生一定的压轴题解题技巧。
如在以二次函数为主要考查点的数学压轴题中,一般需要我们先根据题目中给出的已知条件求各项系数,并以此列出二次函数的解析式,然后再利用如数形结合、分类讨论等数学思想进行解题。
再如在几何题目的解析中,我们就需要充分利用题设条件,并对题目中给出的已知条件进行分析,思考在这一条件下我们还能获得哪些第二已知条件,继续慢慢地让复杂的几何题目变成我们熟悉的习题,然后再对其进行数学分析和作答。
二、案例分析——以安徽2019 中考数学压轴题为例
当我们具备了一定的压轴题解题心理和解题技巧以后,就应该尝试着进行压轴题解题训练,本部分我将以2019 年安徽省中考数学卷的压轴题解题分析为例,浅谈压轴题的解题方法。
1.题目
如 图1,Rt △ABC中, ∠ACB=90 °,AC=BC,P为 △ABC内 部 一 点, 且∠APB=∠BPC=135°。

图1
(1)求证:△PAB∽△PBC;
(2)求证:PA=2PC;
(3)若点P到三角形的边AB,BC,CA的距离分别为h1,h2,h3,求证h12=h2·h3。
2.第一小问
第一问主要考查的就是对已知条件的把握,是关于三角形相似的证明问题,在看到这个问题时,我们首先应该想到如何证明相似。在初中数学的学习中,证明两个三角形相似的方法主要有三种:证明两角对应相等;证明两边对应成比例且夹角相等;证明三边对应成比例。在这个问题的解答中,题设条件中明显关于角大小的条件较多,因而在解题时我们就可以根据题设条件,用第一种证明方法,通过求△PAB与△PBC这两个三角形中两个角的度数相等,证明三角形相似。故此题的答案应为:
∵∠ACB=90°,AB=BC,∴∠ABC=45°=∠PBA+∠PBC。
又∠APB=135°,∴∠PAB+∠PBA=45°,∴∠PBC=∠PAB。
又∵∠APB=∠BPC=135°,∴△PAB∽△PBC。
3.第二小问
在这个问题中,我们要考虑到勾股定理的用法,即等腰直角三角形中斜边等于直角边的 倍,然后利用第一小问中的相似结论,根据勾股定理对题目进行简单分析。此题的正确解题流程应为:
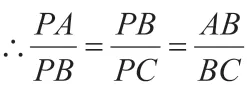
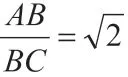
4.第三小问
一般来说,数学压轴题的第三小问才属于真正的压轴题,但是在今年安徽卷的中考数学压轴题中,第三个小问题的难度较往年而言并不算特别大,在这道题目中,只要我们能找准辅助线的作法,并合理利用题设条件及在第一小问、第二小问的解答中获得的第二已知条件,那么解答起来就比较容易。这道题目的正确做法应为:
如图2,过点P作PD⊥BC,PE⊥AC交BC、AC于点D,E。
∵∠CPB+∠APB=135°+135°=270°,
∴∠APC=90°,∴∠EAP+∠ACP=90°。
又∵∠ACB=∠ACP+∠PCD=90°,
∴∠EAP=∠PCD,
∴Rt △AEP∽Rt △CDP,
∵△PAB∽△PBC,

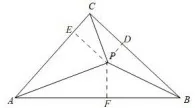
图2
即h12=2h22=2h2·h3=h2·h3。
总之,压轴题是为了让学生的考试成绩更有区分度,所以在实际教学中,我们并不用要求每个学生都能将其解答出来,但是不能做出整道题不代表一点不会,因而在教学过程中,我们应该努力为学生梳理清楚数学知识和数学方法,让学生最大限度地发挥出自己的实际水平,尽可能得到数学高分。
